基于多点地质统计学的密井网储层建模方法研究
2022-03-29韩智颖
韩智颖




摘 要:系統介绍了多点地质统计学的基本原理以及与传统建模方法的区别。以胜利油田A区为例,在利用训练图像指导模拟的基础上,深入分析了砂泥岩比例、参考比例、垂向比例函数、概率趋势体等各项敏感参数对模拟结果的不同影响,提出了通过调整敏感参数来提高预测结果准确性的新方法;并从训练图像选取、提高模型确定性、无井控制区随机模拟等方面开展研究,确定了适合研究区的最优参数。同时,利用平面展布特征分析、不同模拟方法结果对比、抽稀井验证等方法,对研究区沉积相模型的预测精度进行了验证。实践结果表明,利用该方法得到的沉积相模型能够实现砂体平面展布特征和纵向叠置关系的准确预测,预测结果与实钻井及实际地质认识基本吻合,同时对于河流相砂体“顶平底凸”的地质特征也具有较好表征,对于密井网区河流相砂体研究具有较大的指导意义,可为其他同类型油藏的储层预测研究工作提供方法指导。
关键词:多点地质统计学;训练图像;敏感参数;随机模拟;储层建模
中图分类号:TE343 文献标志码:A 文章编号:1003-5168(2022)4-0117-06
DOI:10.19968/j.cnki.hnkj.1003-5168.2022.04.026
Research on Reservoir Modeling in Dense Well Pattern Area Based on Multi-Point Geostatistics
HAN Zhiying
(Geophysical Research Institute of Shengli Oilfield Branch Co., Dongying 257022, China)
Abstract: This paper introduces the basic principle of multi-point geostatistics and its difference with traditional modeling methods. Taking Gudong 2th block in Shengli Oilfield as an example, on the basis of using training images to guide the simulation, In this paper, the different influences of sensitive parameters such as sand-shale ratio, reference proportion, vertical proportion function and probability trend body on the simulation results are deeply analyzed, and a new method is proposed to improve the accuracy of the prediction results by adjusting sensitive parameters. The optimal parameters for the study area were determined by the selection of training images, the improvement of model certainty, and the stochastic simulation of the non-well controlled area. At the same time, the prediction accuracy of the sedimentary facies model in the study area was verified by the analysis of plane distribution characteristics, the comparison of the results of different simulation methods, and the verification of reduced wells. Practice results show that using this method to get the model of sedimentary facies, sand body can be implemented plane distribution characteristics and vertically superimposed relationship of accurate prediction. The predicted results are basically consistent with the actual drilling and geological understanding, and the geologic features of fluvial facies sandstone also has a good characterization. It is of great guiding significance to the study of fluvial facies sandstone in dense well pattern area and can provide methodological guidance for the research of reservoir prediction of other similar reservoirs.
Keywords: multiple-point geostatistics; training images; sensitive parameters; stochastic simulation; reservoir modeling
0 引言
地质统计学是20世纪60年代发展起来的应用数学学科中的一门分支,它利用变差函数来描述地质变量的相关性和变异性,被广泛应用于空间建模领域。但基于变异函数的传统两点统计学方法仅能表达空间中两点之间的相关性,不能充分描述具有复杂几何形状的砂体,储层非均质性描述效果差。为了弥补传统地质统计学的不足,引入了多点地质统计学方法。该方法应用“训练图像”建立多点之间的相关性,能够准确表达实际储层结构、几何形态及其分布模式,建立的沉积微相模型更具地质意义[1]。
本研究以胜利油田A区Ngs3-4小层为例,运用多点地质统计学方法,开展密井网条件下的储层建模技术研究。在以训练图像为指导的原有研究模式上,提出通过调整各项敏感参数来修正模拟结果的新方法,进一步提高预测结果的准确性,得到符合沉积规律且忠于井信息的高精度油藏模型,为后续油藏精细描述奠定坚实的基础。
1 多点地质统计学的基本原理
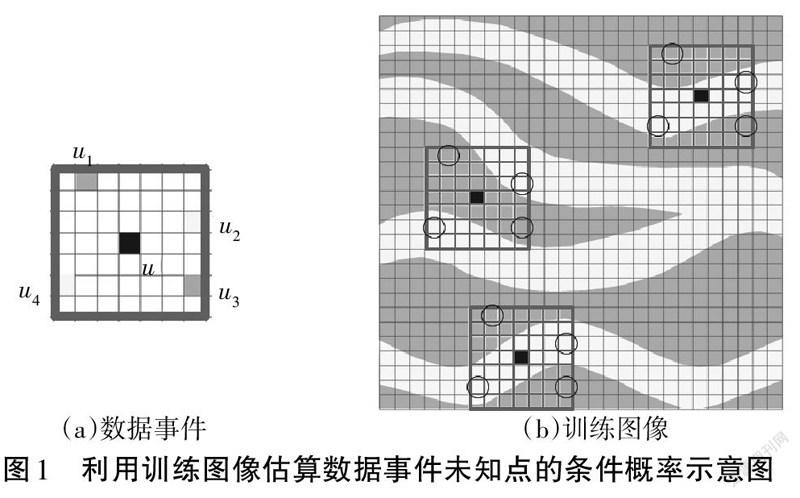
多点地质统计学的关键是增加了训练图像作为约束。训练图像是地质概念模型的数值表示,是多种数据体的综合表达,能够描述空间属性变化的基本规律,其作用相当于两点统计学中的变差函数。多点地质统计学通过扫描训练图像寻找与未知数据事件完全相同的事件个数,从而确定未知点的概率分布,它能够反映空间中多点之间的相关性,实现复杂空间结构和几何形态的准确表达[2-5]。其基本原理如下:
已知一个以u为中心,大小为n的数据事件dn和一个反映储层和非储层分布的训练图像,数据事件可表达为d={Su=s,α=1,…n},对该数据事件进行预处理,对训练图像进行扫描。当训练图像中的一个扫描结果与数据事件d相同时即为一个重复,统计训练图像中的总重复数c(d)和在Sk状态下的重复数c(d),此时c(d)与c(d)的比值就是该数据事件dn的概率,由此可得到未知点u的预测结果,其条件概率分布函数可表达为:
Prob{S(u)=S|S(u)=Skα;α=1,…n}c(d)/c(d) (1)
其中:u為第α个向量点,S(u)为不同向量点组合,d为以n为大小的数据事件,c(d)为数据事件的重复数。
例如,图1(a)中的数据事件由一个未知中心点u和4个已知向量点u~u组成,其中u和u为非储层,u和u为储层,应用该数据对训练图像进行扫描,得到图1(b)中的3个重复,即c(d)=3;通过统计,得到未知点为储层的重复为2,未知点为非储层的重复为1。因此,该未知点为储层的概率为2/3,为非储层的概率为1/3。
2 基于多点地质统计学的密井网储层建模研究
2.1 区块概况
A区构造整体是一个中间高、边部低的牵引背斜构造,主力含油层系是上第三系馆陶4-6砂组,平均孔隙度为33.2%,平均渗透率为1 491×10 μm,属于高孔-高渗储层。A区自投产以来,先后经历了天然能量开采、注水开发、井网调整、综合调整、注聚开发和产量递减6个阶段,目前处于特高含水、低采出程度开发阶段。A区东部井网密度较高,最小井间距仅为27 m,但由于A区储层非均质性强,预测难度大,即便在高井网密度下依然存在注采矛盾突出、油水关系混乱等问题,难以满足精细开发需求。为了确保研究的准确性,在A区选取了井网密度较高的一块区域进行研究,研究区面积2.1 km,总井数163口,平均井网密度78口/km,平均井间距113 m,目的层为Ngs 3-Ngs 4,共10个小层。
2.2 训练图像选取
训练图像是用来储存研究区地质模式的数据库,能够反映沉积相空间几何形态、结构及其分布特征。可以通过地质露头、手绘图、地质认识、相似的成熟油藏模型、基于目标的模拟、物理模拟试验等形式获得。利用训练图像进行预测,应具有足够多相同局部训练模式的复制品,即训练图像是平稳的;其次,为了能够全面反映沉积的横向迁移作用和垂向加积作用,训练图像应是三维的;另外,训练图像应该相对简单,沉积相类型不能过于复杂[6]。根据上述原则,在A区精细地层对比和沉积相研究的基础上,绘制各个小层的沉积微相图,同时利用密井区各类沉积微相在不同层位上的定量统计数据,采用确定性建模的方法建立了沉积相模型,在此基础上结合垂向砂泥岩比例曲线,建立了研究区的三维训练图像。
2.3 敏感参数分析
在训练图像的指导下,利用多点地质统计算法进行随机模拟,此时得到的预测模型基本能够反映研究区砂体的几何形态,但对砂泥岩含量进行统计对比后发现:模拟得到的砂岩含量为37.3%,泥岩含量为62.7%,原始测井数据的砂岩含量为27.2%,泥岩含量为72.8%,误差为10.1%。由此可见,仅仅利用训练图像进行控制,其模拟结果的准确性较低,对于A区这样的开发老区来说,预测精度还需要进一步提高。经研究发现,在模拟过程中存在对预测结果相对敏感的一系列参数,包括砂泥岩比例、参考比例、垂向比例函数、概率体,通过对这些敏感参数的调整优选,能够有效提高模拟结果的准确性。
2.3.1 砂泥岩比例。利用多点地质统计算法进行模拟时,在给定的训练图像下,系统会根据已知数据自动默认某个砂泥岩比例值。以A区Ngs3-2小层为例,该小层原始测井砂泥岩含量为0.162/0.838,系统默认的砂泥岩比例为0.381 6/0.618 7,由于之前模拟结果的砂岩含量比原始测井数据的砂岩含量高,因此分别研究了砂泥岩比例为0.35/0.65、0.3/0.7、0.25/0.75、0.15/0.85时的模拟结果。结果显示,设定的砂泥岩比例与原始测井数据越接近,模拟得到的数据误差越小,但由于多点地质统计算法的随机性,模拟结果的砂体形态预测精度也越低,砂体变得零散破碎,与实际地质认识不符。因此,综合考虑上述因素,当砂泥岩比例为0.3/0.7时,模拟结果最准确[7]。
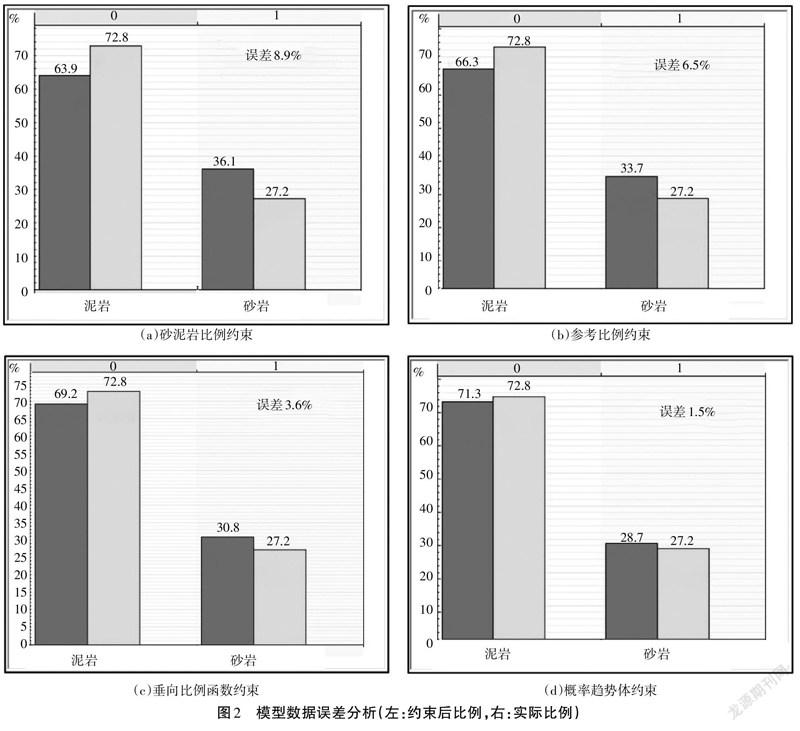
利用该方法,对研究区各小层砂泥岩比例均进行了调整,调整后模型误差从10.1%降为8.9%,如图2(a)所示[8]。
2.3.2 参考比例。参考比例表示所给砂泥岩比例的参考权重,如果参考比例为1,则会根据所给砂泥岩比例进行模拟;如果参考比例为0,模拟时会优先考虑模拟砂体的几何形态,所设定的砂泥岩比例的影响较小。通常默认的参考比例为0.5,为了明确该参数的影响,以Ngs3-2小层为例,比较了砂泥岩比例为0.3/0.7的前提下,参考比例分别为0.3、0.5、0.7、1.0时的模拟误差,其结果如表1所示。从表1中可以看出,当参考比例为0.7时,预测结果最准确。
利用该方法,对研究区各小层的参考比例均进行了调整,调整后模型精度明显提高,模型误差从8.9%降为6.5%,如图2(b)所示。
2.3.3 垂向比例曲线。垂向比例曲线是通过统计各小层内部不同沉积相类型在垂向各网格体中的分布比例变化,来约束模拟结果,利用垂向比例曲线进行约束能够使模拟结果保持统一的概率分布,提高模型的纵向预测精度。在上述研究的基础上,对各个小层增加了垂向比例曲线作为约束,约束后的砂体预测更加精准,模型误差从6.5%降为3.6%,如图2(c)所示。
2.3.4 概率趋势体。概率趋势体反映了不同沉积相在各个位置的概率大小,是垂向比例曲线的标准化,通过对井点处的沉积相数据进行粗化,利用克里金算法来估算出每种相的平均概率,对于无井控制区的沉积微相也具有较好的预测作用。该方法运用变差函数,对不同方向的影响范围进行调整,在模拟基础上增加了地质概念,能够提高模型预测的准确性。利用概率趋势体进行约束后,模型预测误差从3.6%降为1.5%,如图2(d)所示。
2.4 模型预测精度分析
在训练图像约束下,通过对上述敏感参数进行调整,得到了数据误差仅为1.5%的预测模型,但仅利用数据误差作为评价指标还不够全面,需要对预测结果进行多角度分析。因此,通过对平面展布特征、模拟方法对比、抽稀井匹配情况等因素进行分析,对该预测模型的准确性进一步验证。
2.4.1 平面展布特征分析。将模型所预测的砂体厚度图与井震结合,精细地质研究后得到的砂体厚度图进行对比,对其平面展布特征及砂体发育特征进行分析(图3)。结果表明,预测的砂体分布趋势与地质认识基本一致,砂体厚度中心吻合,平面展布特征预测准确。
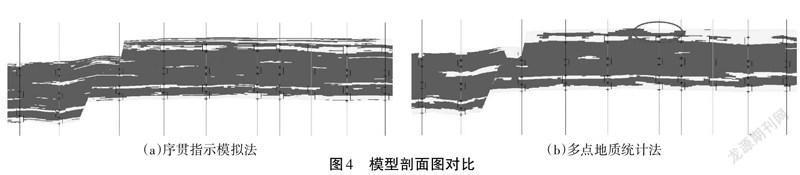
2.4.2 模拟方法对比。将多点地质统计法得到的模拟结果与傳统序贯指示模拟法得到的模型进行对比(图4),从图4中可以看出,多点地质统计法模拟的结果能够更好地反映砂体几何形态,砂体的连续性更好,而且能够清晰地表示出河流相砂体“顶平底凸”的特征。
2.4.3 抽稀井验证。为了对模型的预测精度进行准确验证,在建立模型时对研究区的个别井进行抽稀,剔除这些井的井点数据,建立模型后再将这些抽稀井的岩相数据投影到预测模型剖面图上(图5),从而对预测砂体位置和形态的准确性进行验证。从图5中可以看出,预测结果与抽稀井的砂体位置完全吻合,且砂体厚度基本一致,预测结果准确度较高[9]。
2.5 应用效果分析
在上述研究的基础上,通过精细地质研究,利用砂厚控制面、单井数据及地质成果约束建立高精度油藏地质模型。并在上述沉积相模型的控制下,结合研究区单井孔渗数据,应用随机模拟方法建立孔渗物性模型[10]。
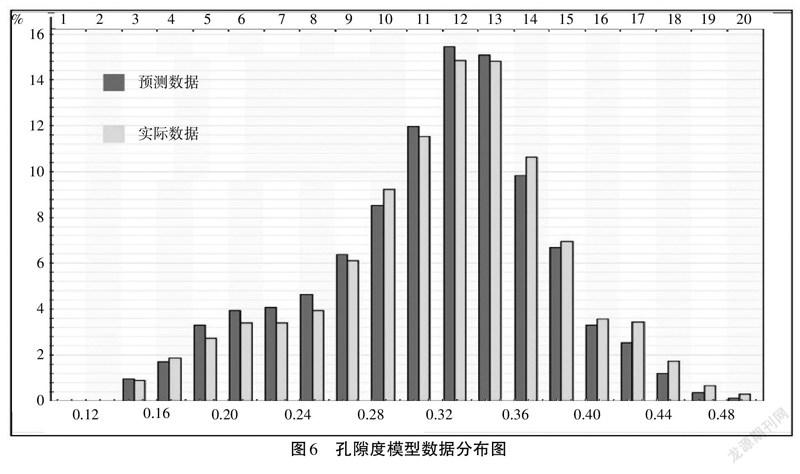
2.5.1 模型数据统计分析。分别统计了研究区各个小层岩心测试的平均孔隙度和平均渗透率,将模型预测结果与统计数据进行比较。对比结果如图6,由图6可以看出,各小层孔渗模型分布特征与岩心测试数据较为吻合,整体规律基本一致。
2.5.2 孔隙度模型分析。对孔渗模型进行了精度分析,结果表明,模型在井点处与井资料吻合,忠实于实际数据;且该模型对于砂体形态的预测十分精细,实现了砂体横向展布和纵向叠置关系的精细刻画。
2.5.3 储层展布分析。如图7(a)所示,基于多点地质统计学的密井网储层建模技术建立的砂体模型能够清晰地刻画河道形态,点沙坝、河漫滩等河流相砂体沉积模式也能得到清晰体现,与实际地质规律相一致。
另外,砂体模型不仅实现了河流相砂体横向展布、下切河道及纵向叠置关系的精细刻画,同时进一步提高了储层识别能力。经检验,薄砂体最大识别精度小于2 m,隔夹层识别精度小于0.5 m,如图7(b)所示。
3 结语
①多点地质统计学应用“训练图像”建立多点之间的相关性,能够准确表达实际储层结构、几何形态及其分布模式,与传统建模方法相比,该方法在储层预测方面具有明显优势。
②在油藏建模过程中,砂泥岩比例、参考比例、垂向比例函数、概率趋势体等敏感参数对于提高模型确定性具有较大作用,可以通过反复尝试和参数优选,有效提高模型预测精度。
③应用概率趋势体约束得到的模型预测效果较好,且对于无井区也能控制数据随机产生的概率,预测精度较高。
④基于多点地质统计学的密井网储层建模技术在胜利油田多个区块取得了良好的应用效果,实现了砂体展布规律的有效预测,对于密井网区河流相砂体研究具有较大的指导意义,可为其他同类型油藏的储层预测研究工作提供方法指导。
参考文献:
[1] 吴胜和,李文克.多点地质统计学:理论、应用与展望[J].古地理学报,2005 (1):137-144.
[2] 赵学思.多点地质统计学反演方法研究[D].荆州:长江大学,2018.
[3] 陈欢庆,李文青,洪垚.多点地质统计学建模研究进展[J].高校地质学报,2018 (004):593-603.
[4] ZHANG T F.Incorporating geological conceptual models and interpretations into reservoir modeling using multiple-point geostatistics [J].地学前缘,2008(1):28-37.
[5] 潘少伟,王家华,杨少春,等.基于多点地质统计方法的岩相建模研究[J].科学技术与工程,2012(12):2805-2809.
[6] 王家华,马晓鸽.多点地质统计学在储层建模中的应用[J].石油工业计算机应用,2012(2):15-16.
[7] 熊哲,严锡,金杨波.油藏地质建模中多点训练图像应用研究[J].江汉石油职工大学学报,2012(4):1-2.
[8] 李涛涛,魏波.应用petrel进行多点统计地质建模的实践[J].石化技术,2015(11):105.
[9] 尹艳树,吴胜和,秦志勇.目标层次建模预测水下扇储层微相分布[J].成都理工大学学报(自然科学版),2006(1):53-57.
[10] 孙玉波.河流相砂体地质建模方法[D].秦皇岛:燕山大学,2014.
