混合单调算子不动点定理的拓展研究
2022-03-28尚珍珍张小勇寇海荣
尚珍珍,张小勇,寇海荣
(太原学院 智能与自动化系,山西 太原 030032)
0 引言
混合单调算子自郭大钧[1]及Lakshm ikantham V[2]提出以来就获得广泛关注,大多在巴拿赫空间[3]中进行研究。Bhaskar等[4]推出了混合单调的概念,并介绍混合单调映射和耦合不动点的相关概念。半序方法对于研究非线性方程(组)的解以及非线性算子不动点[5]的存在性有着十分重要的意义。近年来,主要研究关于半序度量空间中不动点的存在性以及算子方程的可解性[6-8]。
本文进一步研究混合单调算子不动点存在的惟一性,并证明了一些新的不动点定理,拓展了现有文献的一些结论。
定义1 Bhaskar and Lakshmikantham[4]
如果A(x,y)对每一个固定的y∈Y关于x是增的,对每一个固定的x∈X关于y是减的,那么二元算子A:X×X→X为混合单调算子。
定义2
设(X,≤)是半序集[5],X×X产生的空间是半序度量空间,有(x,y),(u,v)∈X×X,(u,v)≤(x,y)⟺x≥u,y≤v。如果x=G(x,y),y=G(y,x),则(x,y)∈X×X是其耦合不动点。
定理1 Bhaskar and Lakshmikantham[4]
设(X,≤)是半序集,(X,d)是一个完备度量空间,G:X×X→X是连续映射,或者X有以下属性:
1)如果有一个非减序列{xn}→x,对∀n∈N,有xn≤x;
2)如果有一个非减序列{yn}→y,对∀n∈N,有y≤yn;
假设∃k∈[0,1],使得对∀x,y,u,v∈X,x≥u,y≤v,有
(1)
如果∃x0,y0∈X,则
x0≤G(x0,y0),y0≥G(y0,x0)
(2)
那么,∃x,y∈X,使得x=G(x,y),y=G(y,x)。
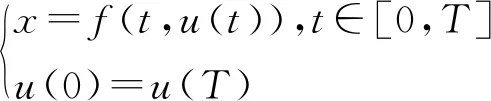
定理2 Lakshmikantham and C′iric′[9]
设(X,≤)是偏序集,(X,d)是一个完备度量空间。有两个映射关系G:X×X→X,g:X→X。
假设∃φ(t) (3) 分析:可以看出,定理2在定理1的基础上进行了改进,将压缩常数k改进为函数φ(t),事实上通过这种改进,压缩条件更加宽松。 在文献[10]和文献[11]中关于混合单调算子有了新的研究成果,具体分析在混合单调算子的研究中的一些情况,使用新的度量空间(X2,d2),减少半序度量空间中耦合巧合和耦合不动点的条件,进而得到相应的结果。 定理3 Berinde[3] 设(X,≤)是半序集,(X,d)是一个完备度量空间。G:X×X→X是连续映射。假设∃k∈[0,1],则对∀x,y,u,v∈X,x≥u,y≤v有: (4) 定理3是Berinde证明的,压缩条件显然范围更广,把不等式左端的一项变成对称的两项,得出定理4: 定理4 设(X,d,≤)是半序度量空间,有两个单调映射关系G:X×X→X,g:X→X。 假设φ:[0,∞]→[0,∞],φ(0)=0, 且是右上半连续的。对∀x,y,u,v∈X,g(x)≤g(u),g(y)≥g(v)均有 (5) 那么∃x0,y0∈X,使得 g(x0)≤G(x0,y0),g(y0)≥G(y0,x0) (6) 分析:可以看出,定理4中的式(5)是在定理2压缩条件的基础上进行修改的,不等式左端由一项变成了对称的两项和的形式,证明分析如下: 因此,通过压缩条件式(5),得到一个巴拿赫型压缩形式: d2(S(x,y),S(u,v))≤φ(d2((gx,gy),(gu,gv))) (7) 假设式(6)成立,令初始值(g(x0),g(y0))∈X2,定义有Picard迭代相关特性的S,则序列{g(xn),g(yn)}⊂X2可以定义为: (g(xn+1),g(yn+1))=S(g(xn),g(yn)),n≥0 (8) 遵循巴拿赫的压缩不动点定理证明步骤,在式(7)中令(x,y)=(gxn,gyn)≥(gxn-1,gyn-1)=(u,v),可得: d2(S(gxn+1,gyn+1),S(gxn,gyn))≤φ(d2((g(gxn),g(gyn)),(g(gxn-1),g(gyn-1))),n≥1 (9) 用反证法来证明δ=0。因此: (10) (11) (12) 由式(11)、式(12)可得: rk≤φ(δn(k)+δm(k))+φ(rk) (13) 在式(13)中,令k→∞,由于φ(δ)<δ,φ(0)=0,运用式(10)可得:ε≤φ(0)+φ(ε)=φ(ε),这显然是矛盾的。 (14) 通过定理3和定理4可以看出,完全是在压缩条件上进行改进,将等式左端的一项变成两项和的形式,研究结果概括、扩展、补充了Harjanietal[12]和RazaniParvaneh[13]建立的耦合不动点定理。另外,使用本文方法可以得到多个变量公共不动点的结果,在半序度量空间可以拓展由一个变量得到的常见不动点结果。在今后的研究中,会将本文研究的不动点定理运用到非线性积分方程中。 本文对原有混合单调算子的结论进行了改进,将压缩条件进行变换,采用对称的两项和代替原来的一项,而且将压缩条件的右端改进为函数形式,适用范围更广。使用新的度量空间(X2,d2),减少半序度量空间中耦合巧合和耦合不动点的条件,进而得到相应的结果,获得在某些情况下更普遍的定理。在定理的证明中,主要是证明柯西收敛,运用不等式关系以及相关定义证明所需论证问题。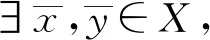
1 不动点定理研究
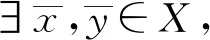
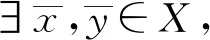
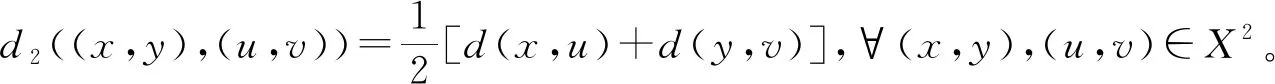
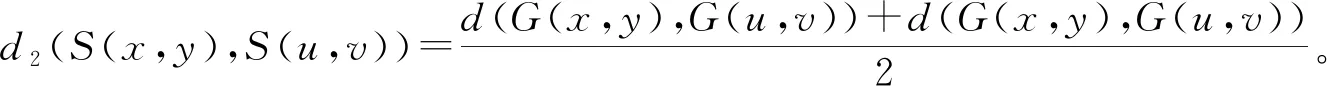
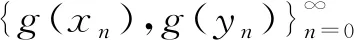
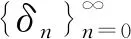
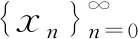
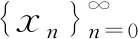
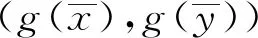
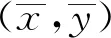
2 结论
