自适应信号注入的无位置传感器电机控制技术

李霄翔，陈龙淼，孙 乐

(1.南京理工大学 机械工程学院，南京 210014；2.南京理工大学 自动化学院，南京 210014)

0 引 言

在伺服电机驱动领域中，无位置传感器电机控制是一个十分热门的研究方向。这种控制方法的主要价值在于，舍弃了传统伺服电机驱动中必不可少的环节：位置传感器，在不使用位置传感器的情况下，依然能够实现伺服电机的闭环位置控制。毫无疑问，这种控制策略将进一步提高电机驱动系统的可靠性并减小系统体积。然而，无位置传感器驱动技术仍未获得广泛应用，其原因在于，无位置传感器驱动技术下，电机的控制精度以及响应速度还远达不到有位置传感器驱动的水平。此外，目前的无位置传感器驱动技术本身亦存在着一些不可靠的问题。

无位置传感器电机驱动技术的不可靠主要体现在低速状态下。在高速范围内，驱动系统可以从电压中提取扩展反电动势[1-2]。在高速情况下，扩展反电动势的幅值较大，驱动系统较容易跟踪其相位角，从而得到电机转子位置。而在低速范围内，扩展反电动势变得比较微弱，难以监测。

高频信号注入法解决了上述难题[3-5]。该方法将高频变化的电压信号注入到d轴电压ud中[6-7]，以此产生高频电流。通过对该电流信号求导，驱动系统就可以根据d，q轴间电感的差异来跟踪气隙的磁凸极性，从而估计出电机转子的实际位置。以上方法在下面电压方程式(1)中可以得到解释。

式(1)的第一项是感应电动势，反映了电机转子的凸极性；第二项是扩展反电动势，其中包含了运动反电动势,其大小正比于电机转速。因此，电机的位置估计就可以看作一个求解式(1)的数学问题。

在此基础上，本文采用了基于凸优化[8-9]的位置估计策略，构造基于式(1)的成本函数并寻求其最小值的方式来进行位置估计。除求解电机估计位置这一基本功能外，成本函数在本文中还被赋予了新的功能。在每一时刻的估计位置求解过程中，成本函数最终收敛到的函数值实际上是凸函数求解精确度的直接体现。本文提出使用成本函数的函数值的方差作为位置估计效果的监视器，动态调整伺服电机的位置估计性能。

当电机处在低速运行状态或突然加速状态时，驱动系统可以根据估计转速以及电流来判断是否开启高频信号注入，以获得更优的低速控制性能。值得注意的是，高频信号注入的幅值会直接影响位置估计的稳定性和运动控制的质量。具体来说，注入信号幅值越高，位置估计越稳定，但相应的运动控制质量会降低[10]，同时也会带来高频噪声。这也是电机高速运行时不使用信号注入的原因。因此，在低速情况下，使用多大幅值的注入信号，权衡位置估计的稳定性与高质量运动控制之间的关系，就成了值得探讨的问题。

综上，本文提出了一种自适应信号注入的无位置传感器电机控制技术。通过使用成本函数的函数值方差作为位置估计效果的监视器，用以动态调节高频信号注入的幅值，实现了高质量的运动控制与稳定的位置估计之间动态且合理的平衡。

1 解析模型

本文描述了自适应信号注入的无位置传感器电机控制技术的概要。通过监视器，驱动系统将可以动态调整高频信号注入的幅值，以提高位置估计的稳定性，权衡其与高质量运动控制的平衡。

1.1 无位置传感器电机控制系统的结构

自适应信号注入的无位置传感器电机控制系统的基本结构框图如图1所示。

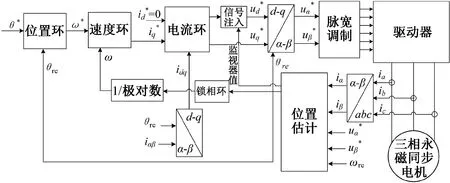
图1 自适应信号注入的无位置传感器电机控制系统结构框图

图1展示了一个经典的级联电机控制系统，其中转子位置和速度不再使用位置传感器，而由估计模块计算得出。同时，为了支持低速状态下的位置估计，驱动系统在d轴电压上叠加了高频信号注入。

当电机估计速度低于阈值速度时，信号注入将被开启，而注入的幅值将由位置估计模块产生的监视器值加以动态调整。当位置估计较为稳定时，即可适当降低注入幅值，以减小高频信号注入对运动控制质量的影响。

1.2 基于凸优化的电机位置估计

本文使用凸优化算法来解决电机位置估计问题。电机在静止坐标系(α，β坐标系)下的电压方程如下：

(1)

式(1)中的电感值包含了转子位置信息：

Lα=L∑+LΔcos(2θre)，Lβ=L∑-LΔcos(2θre)，

通过理论分析，所有的模型参数都可以假设为已知且恒定的，实际电流可以通过传感器得出，因此式(1)中的不确定变量只剩下了转子位置θre，位置估计问题实际上就变成了解一个关于θre的方程。在这一理论前提下，位置估计算法就成了一个简单纯粹的数学问题。文献[11]具体讨论了这一方法，并建立相应的成本函数：

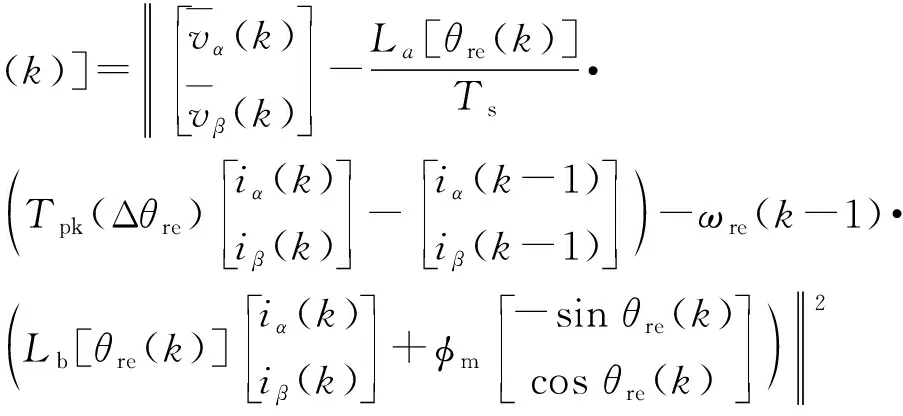
(2)

理论上，如果最终估计出的位置完全符合公式(1)，那么相应的成本函数就将取得最小值。然而，在真实的驱动系统中，采样噪声会破坏方程的平衡，使得成本函数收敛到一个错误的估计位置。为了避免这一问题，系统引入了惩罚项，来抵御估计位置的剧烈变化。即：

式中：K为惩罚项系数。系统采用了牛顿迭代法来求解以上成本函数的最小值问题：

图2展示了一个理想的收敛过程。

成本函数式(3)是一个一元方程，当其二阶导数为正时，必将拥有一个最小值。这也就意味着成本函数实际上是一个凸函数。通过一些合理的近似，成本函数的二阶导数在高速情况下可表示：

2(Ld-Lq)φmid]+2K

(5)

在低速范围内可表示：

图2 凸优化的收敛过程

由式(5)、式(6)不难发现，在高速情况下，电机转速越快，成本函数的二阶导数越大，凸性也就越大，即更容易收敛到最小值。但在低速情况下，由于表贴式永磁同步电机的d，q轴电感差异较小，故成本函数的凸性完全寄希望于电流的导数。也就是说，电流变化越剧烈，成本函数的收敛性能越好，这也是高频信号注入法的意义所在。

从理论上分析，只要成本函数的二阶导数Gθθ>0，驱动系统总能够通过若干次迭代将估计位置收敛到真实值。但在工程实际中，处理器的运算速度限制了迭代求解的次数。本文中的处理器每一次解算仅仅能够提供两次有效的迭代。同时，由于其他原因，如成本函数凸性依旧不够、采样噪声、不准确的模型参数等，真正准确的估计位置总是难以得到，更何况求解器也仅仅只能够迭代两次。换句话说，求解误差在每一步中都真实存在，而相对应的成本函数的函数值则一定程度上反映了误差的大小。

1.3 位置估计效果的监视器

在无位置传感器驱动的实验测试中，驱动系统不会舍弃位置传感器，因为位置传感器测得的真实位置可以用来评判位置估计的准确性。然而在真实的应用环境下，失去了位置传感器这一参照，传统的无位置传感器驱动系统将再也无法得知位置估计算法是否在正常运行。一旦出现意料之外的扰动，会导致收敛误差极大，错误的估计位置将反过来影响电机运动控制，最终势必造成系统的崩溃。在这个过程中，驱动系统由于缺乏相应的评判标准，故没有能力做出相应调整，以阻止系统崩溃。

针对这一问题，传统的无位置传感器驱动系统急需一个监视器，来监测自身的估计状态，以求能够做出动态调整。监视器的功能示意如图3所示。

图3 监视器功能示意

凸优化求解器能够在每一个采样步得出成本函数的函数值。成本函数是用于求解电机的电压方程以得出合适的位置和速度估计值的。估计出的位置、速度信息越准确，成本函数的函数值也就越小越稳定。相对的，如果估计效果不好，函数值将持续处于不稳定状态。

值得注意的是，在驱动系统工作过程中，成本函数的凸性越好，其经过两次迭代后所得的函数值就越小。然而，当位置估计不稳定时，不准确的估计位置将反过来影响到电机运动控制，这也会加剧成本函数值的振荡。因此，当位置估计效果不佳时，较高的成本函数值以及函数值本身的振荡两者叠加，将使得监视器的数值判断变得较为困难。经过以上考虑，较之于成本函数值本身，其方差更能够代表位置估计系统的状态。

拥有了这一方差监视器后，驱动系统就能够知道位置估计模块是否在正常工作了。当监视器值突然变化至一个较大值，驱动系统就有必要采取一些应对措施来稳定系统。例如，更高幅值的高频信号注入可以强行增加低速下成本函数的凸性，以稳定系统。这样做的代价是系统整体的动态响应性能降低以及增加了注入信号带来的噪声，这显然没有位置估计直接崩溃那么严重。图4展示了上述动态调整策略的示意图。

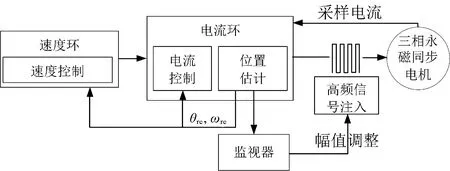
图4 自适应高频信号注入原理

2 方案仿真

本文对使用监视器动态调整高频信号注入幅值的方法进行了仿真验证。表贴式永磁同步电机的参数如表1所示。电机负载为静态制动转矩。

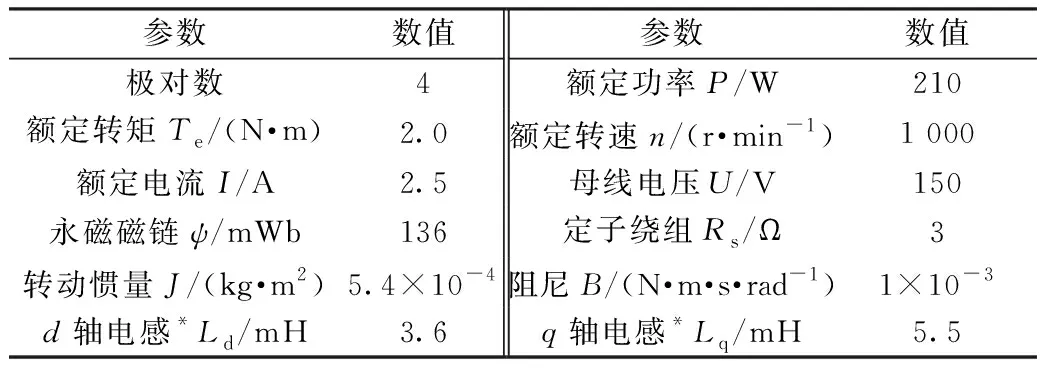
表1 测试电机参数列表

2.1 监视器有效性分析

采用PI控制器对所述系统进行速度环阶跃测试，在整个驱动系统中，转子位置反馈和速度反馈均来自所提出的位置估计器，仿真结果如图5所示。从一开始就为电机施加TL=2N·m的静态扭矩负载。速度阶跃指令100r/min在0.1s出现，随后电机在静态负载下加速。在电流环中有一个恒定的5kHz/20V高频方波注入，以支持低速位置估计。

图5 在2 N·m静态负载下的速度阶跃反馈(速度控制带宽20 Hz,高频注入幅值为20 V)

在图5(a)的加速过程中，可以看到一个很明显的振荡，这是位置估计效果不好引起的。图5(b)展示了位置估计误差，同样可以看到一个明显的误差振荡，与此同时，监视器值也表现出相应的振荡。因此，采用成本函数值的方差作为监视器可以较好地反映位置估计的效果。

图5展示了一个经典的不稳定的阶跃，在此期间估计误差很大，成本函数值波动剧烈，这意味着此时的电流环极其不稳定。为了提升瞬态响应的稳定性，可以考虑采取本文提出的方法，通过提高注入信号的幅值来减小估计误差并提高位置估计的稳定性。

在接下来的讨论中，以图5作为参照，对比采取优化措施后的仿真结果。

2.2 自适应高频信号注入法

本组实验使用完全相同的控制参数重复了图5中的仿真测试。不同的是，本组实验使用成本函数值的方差作为监视器值，以调整注入信号的幅值。当监视器值在150以内时，设置注入信号幅值为20V；当监视器值超过150，注入信号幅值将提高到30V以稳定系统。值得注意的是，虽然图5中的监视器值高达150k，但这是由于位置估计不稳定时，成本函数求解过程中的残差剧烈波动而产生的。实际上当位置估计稳定时，该残差的数值波动是很小的，相应的方差即监视器值就相应很小，一般不会超过100。这就是监视器的阈值较小的原因。而监视器值在位置估计不稳定时的急剧增加也正是其优势所在。对比图5、图6可以发现，改进是十分明显的。图6(b)中的位置估计误差明显小于图5(b)。与持续使用30V信号注入相比，本方案的大多数时间依然采用20V的信号注入，故信号注入对运动控制的影响更小，噪声也更小。

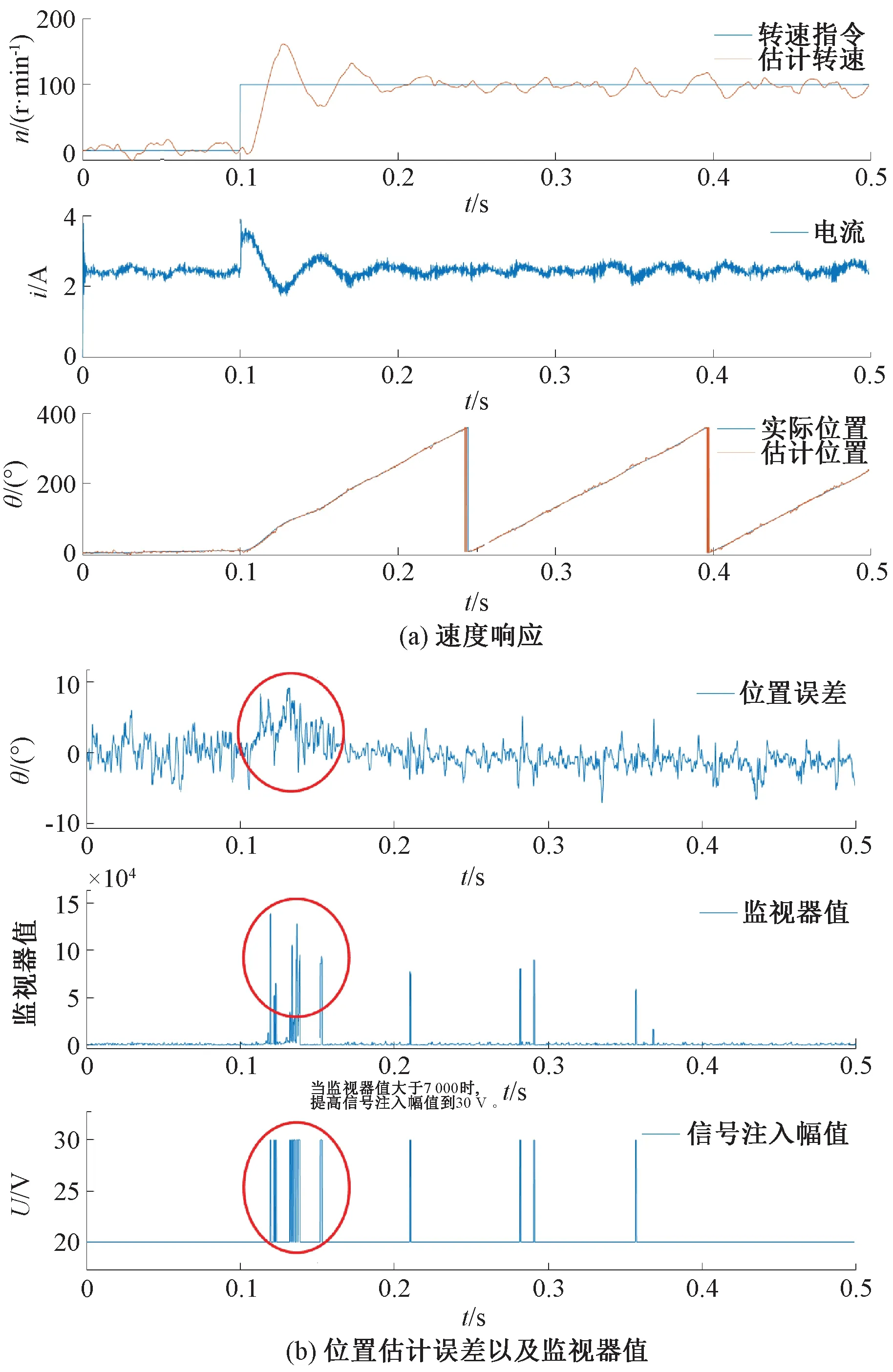
图6 在2 N·m静态负载下的速度阶跃响应(高频信号注入幅值在20 V和30 V之间动态调整)

3 实验验证

为验证本文控制策略以及仿真结果的正确性，搭建了一个电机驱动实验台。三相永磁同步电机经减速器连接到一个磁粉制动器，电机的静态转矩负载可由该磁粉制动器模拟得到。所有控制算法在DSP28379D微控制器上实现，并通过IGBT(型号FS50R07W1E3)实现电机驱动。电流环计算频率、电流采样频率以及开关频率均为10kHz。实验中一些关键变量，例如估计位置、速度误差，监视器值等，均通过上传CAN总线和示波器进行观测。上传CAN总线的数据可以被Simulink观测器实时接收显示。所有实验设施都在图7中做了展示。

图7 用于无位置传感器电机驱动测试的实验装置

3.1 无位置传感器速度控制

在电流环中设置了基于凸优化的位置估计策略。在图8(a)中，驱动器驱动电机经历了0～1 000r/min的全转速测试。为确保零转速或低转速下的位置估计效果，在电机转速处于100r/min以内时，为驱动系统增加幅值为50V的高频信号注入；在电机转速处于100r/min～200r/min之间时，采用幅值为20V的高频信号注入；在电机转速处于200r/min～300r/min之间时，采用幅值为5V的高频信号注入；当电机转速高于300r/min时，不进行信号注入。

图8 无位置传感器控制策略下的速度控制实验结果

值得注意的是，当电机转速为500r/min并关闭信号注入时，监视器值将处在一个较低的水平。但随着转速增加到700r/min乃至1 000r/min时，监视器值又随之上升了。这是由于成本函数式(2)中的第三项是与电机转速成正比的，任何电机参数或位置估计的不准确都将被转速放大。并且，成本函数值是一个平方项，它在高速范围内会被急剧放大。但由于高速时电机充分产生了反电动势，因此位置估计的效果并不会受此影响。

图8(b)展示了30r/min时电机的无位置传感器控制情况。图8中，一通道表示估计位置，二通道表示估计误差，三通道表示实际位置，四通道表示相电流，电机转速波动较大是由于磁粉制动器提供的负载转矩并不完全稳定所致，速度控制振荡反过来引起了位置估计误差。

图8(c)展示了300r/min时电机的无位置传感器控制情况。与图8(b)不同的是，控制过程中信号注入在不断地开启与关闭，但这并不影响整个系统的运行。

3.2 低速下的自适应高频信号注入

在全转速测试后，本组实验设置了不同信号注入幅值影响下的0～100r/min速度阶跃测试。

图9(a)展示了三次速度阶跃测试结果(0～100r/min)。第一个测试使用恒定的30V高频信号注入，此时PI速度控制器依然可以较好地完成该阶跃速度测试。图9(a)的第二个测试将信号注入幅值下降到20V，但只要监视器值超过13 000，就将信号注入幅值提高到30V。在这次测试中，动态调节的注入幅值使得驱动系统在位置估计运行稳定的前提下获得了更小的采样噪声、更安静的实验环境以及更优的运动控制质量。在实际测试中触发的30V信号注入远多于图9(a)，这是CAN通信的采样频率太低导致的。以上测试最后在恒定20V的信号注入下进行了重复。

图9 关于使用监视器动态调整注入信号幅值的实验结果

在该注入条件下，如图9(a)所示，虽然电机转速艰难地维持到了测试结束，但整个驱动系统很难保持稳定。实际上，在大多数测试中，20V的注入幅值都不足以支持位置估计。在第三次测试中可以发现许多监视器值的峰值，这都预示着无位置传感器速度控制濒临崩溃。图9中，一通道表示估计位置，二通道表示估计误差，三通道表示实际位置，四通道表示相电流。

图9(b)展示了第一个测试的瞬态过程，其中的电流波形包含高频成分，这是由30V/5kHz的方波信号注入引起的。这也是图9(a)中第一个测试时监视器值较大的原因。图9(c)展示了第二个测试的瞬态过程，该过程有明显改善，首先电流的高频成分比第一个测试更小了，其次整个系统运行过程中的噪声也明显改善。图9(d)则展示了完全由20V信号注入支持的位置估计系统。可以看到，此时的瞬态过程及其不稳定，最终导致了估计的失败。

以上实验验证了成本函数值的方差作为监视器调节信号注入幅值的效果。表2总结了图8、图9的实验结果。

表2 图8、图9实验结论对比

4 结 语

本文的创新点在于，在伺服电机无位置传感器控制策略中引进了凸优化算法的一个独特的产物：成本函数值，以它的方差来作为位置估计效果的监视器。通过调整高频信号注入幅值的方法来动态修正无位置传感器驱动系统的估计误差。该方法的直接效果是在获得较高动态性能和较低噪声的同时，降低无位置传感器控制的不稳定性。

根据此方法，无位置传感器电机驱动技术的可靠性进一步提高。根据位置估计的原理性质，响应速度和精度难以达到使用真实位置传感器的水平，但由于该方法本身不占用任何硬件资源，故完全可以作为传感器失效后的备选方案，或在精度要求不高的场合直接应用。