基于时空距离度量的航迹发现关联算法
2022-03-27杨邦江婷丁亚坤郭蕊吴泳孙祥
杨邦,江婷,丁亚坤,郭蕊,吴泳,孙祥
(中国电子科技集团公司第五十二研究所,浙江 杭州 311121)
0 引言
随着无线传感器技术、无线电探测技术的发展[1],越来越多的设备能够探测、发现并持续跟踪特定区域内的活动目标[2]。在实际应用中,为了保证防控系统的可靠性,避免监控死角,会部署众多的目标探测和跟踪设备,这些设备独立或者协同进行目标探测和持续跟踪[3-4],并实时上报所发现的目标的航迹数据。在这种场景下,系统往往面临如下几个问题:一是多设备交替覆盖布控导致对目标的跟踪数据增多,每个设备都会对发现的目标航迹进行上报,如果不做合理计算,系统会认为环境中出现了大量目标,导致与真实情况严重不符,将极大影响决策者对区域安全状态的正确研判,也可能导致大量的虚警[5];二是某些探测设备不具备目标建航跟踪能力,只能持续探测发现运动目标实时位置,即仅上报时间序列上的散点。本文主要解决目标点迹建航以及航迹关联等问题。
对于航迹关联问题,衣晓和曾睿等[6]提出一种基于K 近邻平均距离的异步航迹直接关联算法,通过对不等长航迹序列间的灰色关联度进行计算,并利用经典分配法进行航迹关联判定。王号等[7]引入Hausdorff 距离,对两个航迹集的相似程度进行指标衡量并将其作为航迹同一性关联依据。李恒璐等[8]提出基于信息熵权的最近邻域数据关联算法,按照熵权法分配各个测量指标的权值,再对计算出的权值应用最近邻域算法进行统计计算,从而改善原算法在单目标跟踪中存在的问题。高峰等[9]提出了广义绝对灰关联、一般灰色关联、B型灰关联、C 型灰关联、T 型灰关联等理论用于航迹融合领域。Tokta等[10]在马氏距离理论基础上对时间序列做协方差计算实现了航迹关联。周尧等[11]针对某些测试环境下或设备工作状态下目标试验数据原始数据差异较大的问题,提出基于支持度的多传感器融合方法。李捷等[12]针对多周期数据融合问题,基于改进DS(Dempster-Shafer)理论,结合贝叶斯改进方案拟合多源数据的分布情况,建立基于叠合度的融合模型。李素等[13]采用K-means聚类的方法将来自各传感器的局部航迹与系统航迹进行关联,并将系统航迹作为初始聚类中心,避免了K-means 算法本身依赖初始值的缺陷。另一类基于深度学习的方法也有相关应用,黄虹玮等[14]将长短期记忆网络引入CNN(Convolutional Neural Networks)模型提升了航迹关联的精度。
考虑目标航迹数据的空间特性以及时间特性,同时结合数据分类思想,本文设计提出基于时空距离度量的航迹发现关联算法。
1 基于时空距离度量的航迹发现关联算法设计
K-近邻方法(K-Nearest Neighbor,KNN)在机器学习分类问题方面有着较多应用[15-17]。对于待分类数据,KNN 通过在训练数据中寻找出欧氏距离最近的K 条数据,其中最多的类别数据作为分类结果。针对目标运动点迹数据的时空特性,本文在传统KNN 算法的基础上,提出基于时空距离度量的无监督KNN 航迹发现关联算法。
1.1 时空距离度量模型(TSMM)
对点迹进行航迹关联,如果仅考虑单个数据点之间的空间距离,由于存在目标运动轨迹交叉的情况,会存在较大错误率[18-19],如图1 所示。
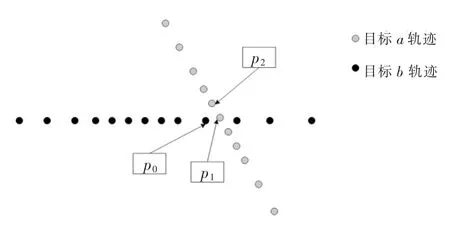
图1 目标飞行示意图Figure 1 Schematic diagram of target flight
此外,当两个目标在不同时间以相同或近似航迹飞行时,航迹在空间上高度重合,仅基于空间位置的度量方法会得出误差较大的结果[20-21]。基于以上考虑,结合目标运动点迹数据实际场景,提出基于时空距离的度量模型(Time-Space Metric Model,TSMM)。
TSMM 主要考虑空间距离、向量距离、时间距离因素,如式(1)所示。
其中,Ta为显著因子,用来对计算结果做显著性缩放处理,避免软件实现过程中因精度丢失问题导致结果异常;TS为数据时间段分布参数,时间差大于此值的数据,需要考虑时间因素对计算结果的影响;t1,t2分别表示两个数据点的时间戳,如果数据时间差小于此值,空间距离和向量距离对最终计算结果影响更加显著;dV表示数据向量的欧氏距离;dS表示数据向量表示的目标点的空间距离。
1.2 基于时空距离度量的改进型KNN 点迹建航算法(TSMM-KNN)
基于时空距离度量的改进型KNN 点迹建航算法(TSMM-KNN)主要分为四个阶段:点集数据预处理阶段、已识别航迹关联匹配阶段、K-近邻数据集相同点集识别匹配阶段和计算结果输出阶段。算法整体流程如图2 所示。
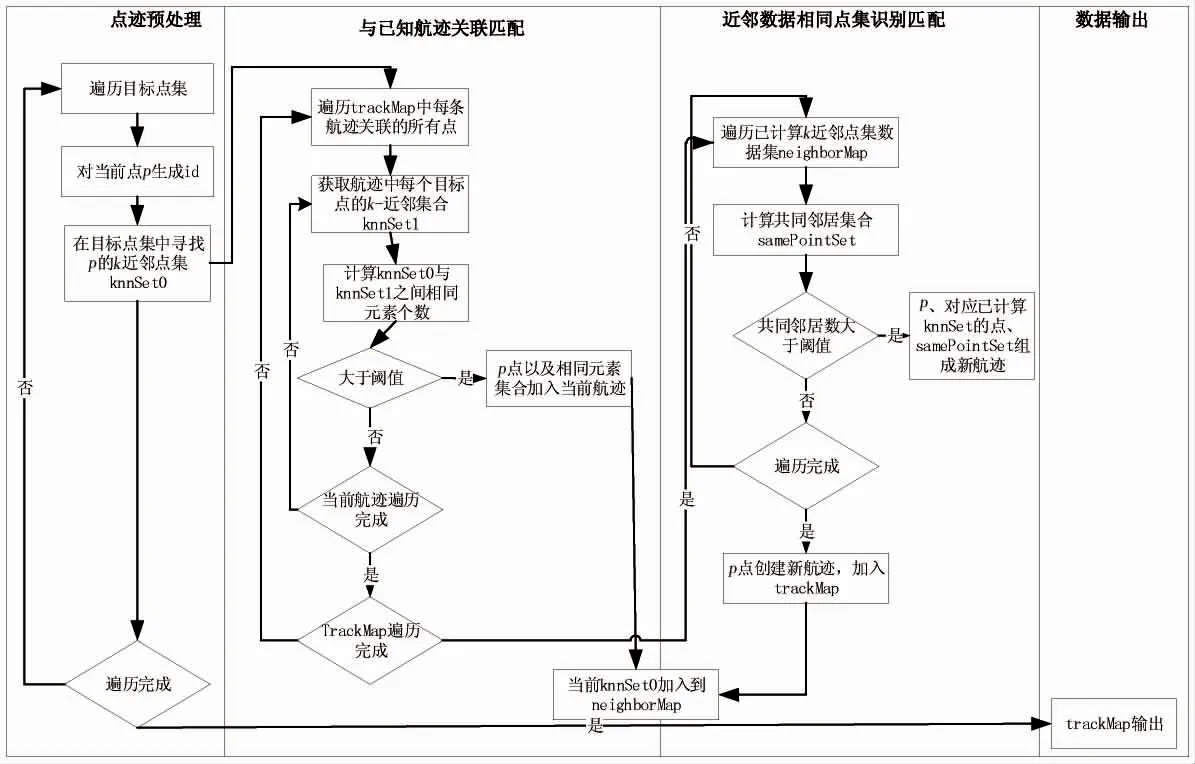
图2 TSMM-KNN 流程图Figure 2 TSMM-KNN flow chart
点集数据预处理阶段作为处理流程的起始,负责处理流程控制功能以及对目标数据格式化处理。由于点迹数据不存在航迹编号批号,所以对点迹数据预生成标识,使用前文提出的TSMM 模型在目标点集中寻找距离量度结果最小的K 个邻居点。
在航迹关联匹配阶段,如果两个点的共同邻居数大于MIN_NUM_SAME_NEIGHBOR值,则将两个目标点以及它们的共同邻居点编入同一航迹。
K-近邻数据集相同点集识别匹配阶段是在前序阶段未成功关联到已有航迹的情况下,与所有未关联航迹的数据进行邻居关联匹配。
2 实验及分析
2.1 实验数据集情况
航迹数据基于对大疆MAGIC3、大疆MINI2、大疆FPV 机型的测试飞行数据进行预处理得到47条航迹数据,其中真实目标数量30 个。实验基本内容是对K 值与MIN_NUM_SAME_NEIGHBOR 参数进行碰撞优化,实验K 参数从8 到20,每个K 参数对应MIN_NUM_SAME_NEIGHBOR 从3 到K 进行实验。此章节中图表横坐标表示MIN_NUM_SAME_NEIGHBOR 参数取值。纵坐标表示对应指标结果值。
2.2 指标定义和结果分析
同航迹数据聚类识别正确率F1:
式中:n 表示识别结果中航迹总数;N 表示真实航迹数;ACi表示第i 条航迹识别结果正确率,对于第i 条识别航迹,记其中识别出总点数量为m,其中同属于一个目标运动航迹的最大点集中点的数量为p,则表示识别出的航迹数与实际航迹数之间的差距情况。如果F1值越小,则说明识别结果中同航迹中数据混杂情况越严重。F1值越大,航迹点集识别越可靠。
从如图3 所示F1指标曲线可以看到,算法在两个参数变化时有明显的效果优化过程。在MIN_NUM_ SAME_NEIGHBOR/K 值达到0.6 左右以后开始呈现较好效果。其意义在于,对于同一航迹上的数据点,其共同邻居数大都能达到设定K值的0.6 以上水平,如果MIN_NUM_SAME_NEIGHBOR 设定较低,会导致不同航迹上的点被归入同一航迹的情况增加。
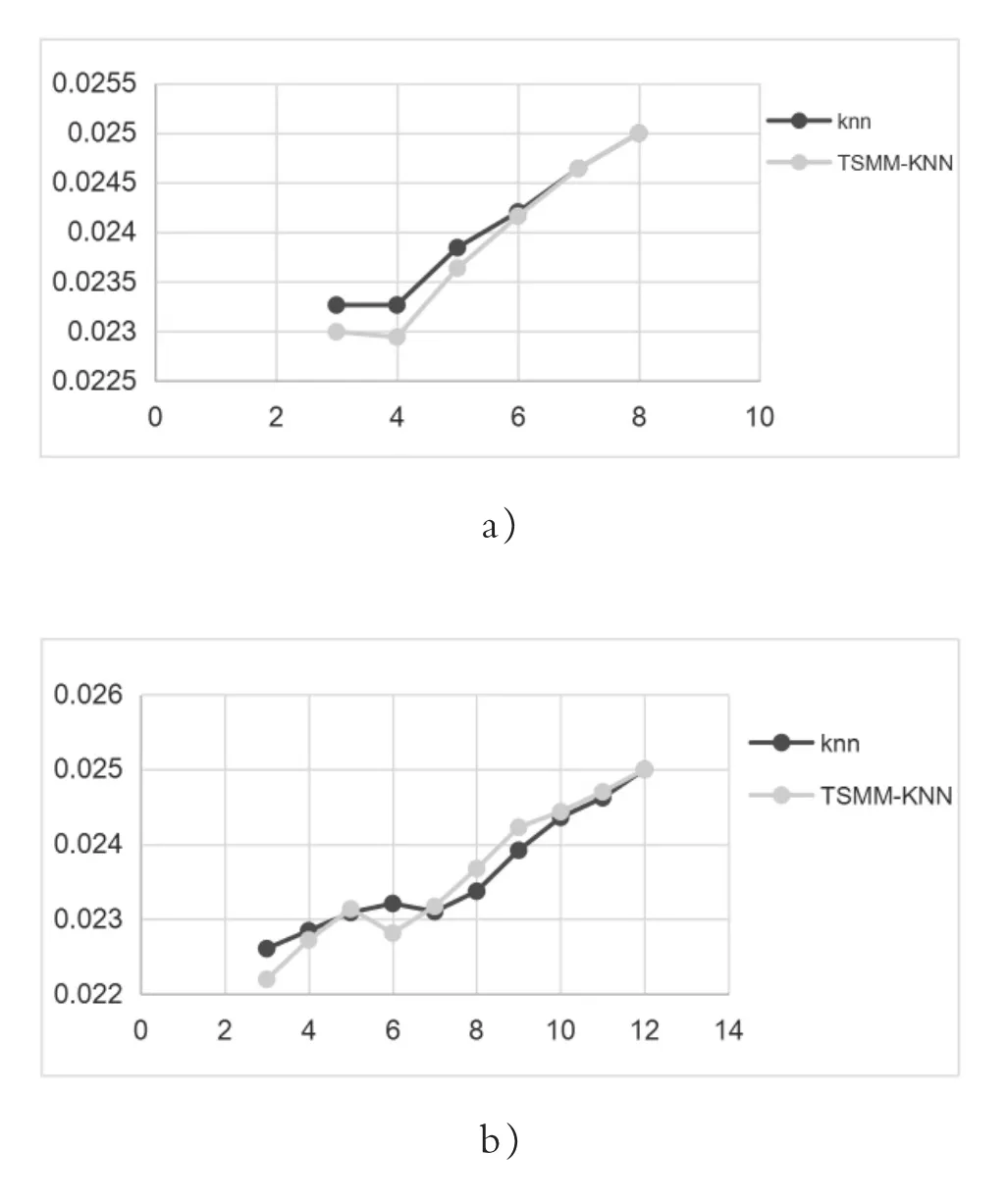
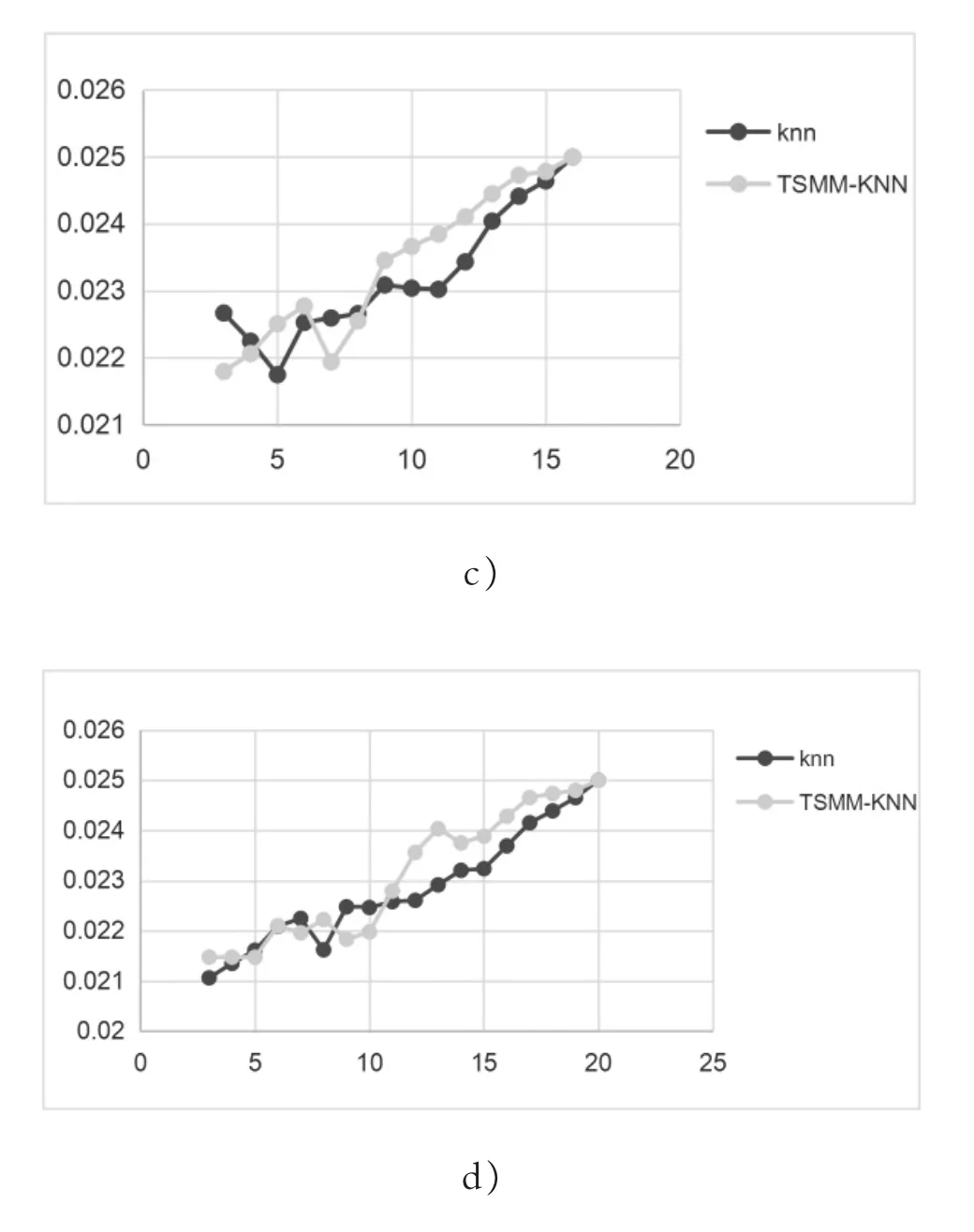
图3 F1 指标曲线a)K=3 b)K=12 c)K=16 d)K=20Figure 3 Index F1 Curve a)K=3 b)K=12 c)K=16 d)K=20
航迹分割评价指标F2:
式中:predTi表示在预测结果中,有原航迹数据集中的Ti航迹中的数据点分布的不同航迹的数量;N 表示原航迹数据集中真实航迹数量。F2指标度量算法对航迹的持续识别能力:F2值越小,则表明航迹被识别得更完整;如果F2值较大,表明航迹被识别成多段暂时航迹的情况较多。
由图4 所示的F2指标对照情况可以看出,TSMM-KNN 相对传统只基于空间距离的KNN 方法拥有更好的航迹分割控制性能,TSMM-KNN 能够更好地让原航迹中的点聚集在同一结果航迹中,降低原航迹被过分识别成大量暂时航迹点的情况。
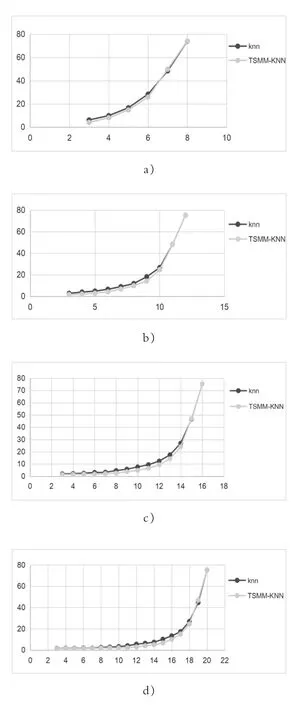
图4 F2 指标曲线a)K=8 b)K=12 c)K=16 d)K=20Figure 4 Index F2 Curve a)K=8 b)K=12 c)K=16 d)K=20
识别结果综合评估指标G:

当同航迹数据聚类识别正确率F1指标与航迹分割评价指标F2都取得较好结果的情况下,综合指标G 才更加优秀。
由图5 所示的指标G 的对照结果可以看出,TSMM-KNN 方法的综合结果相对于只基于空间距离度量的传统方法有显著优化效果。
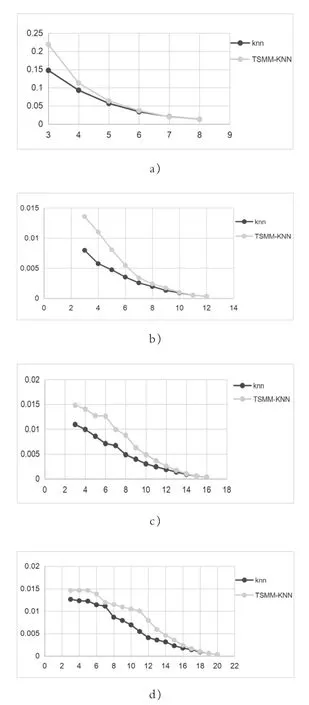
图5 G指标曲线a)K=8 b)K=12 c)K=16 d)K=20Figure 5 Index G curve a)K=8 b)K=12 c)K=16 d)K=20
3 结语
本文利用目标点迹数据的时空特性,充分考量点迹数据之间的时空距离,结合KNN 数据分类理论,实现对大量点迹进行快速准确的航迹发现和关联。相对于只采用空间距离信息的方法,本方法在同航迹数据聚类识别正确率、航迹分割评价指标以及综合评价指标上都获得了更加优秀的表现。算法在数据融合系统中已有相关实践应用。实践证明,该方法具备与数据融合系统快速集成的能力,特别是航迹数据融合系统,此算法的应用能够有效弥补传统航迹融合系统对未建航迹的目标点迹数据无法有效处理的问题。未来,本文将在时间分布不均匀的数据处理方面以及设备异常数据有效过滤等方面做进一步研究,提高算法对异常数据以及时间稀疏性不均匀数据的适应性和容忍度。
