计及柔性直流的短路比指标分析研究

黄楚茵 夏成军 钟明明

计及柔性直流的短路比指标分析研究

黄楚茵1,2夏成军1,2钟明明1,2

（1. 华南理工大学电力学院，广州 510640；2. 广东省新能源电力系统智能运行与控制企业重点实验室，广州 510663）

电力系统的运行特性与其所连接的受端交流电网强度关系密切，而基于传统常规直流系统提出的短路比是衡量受端电网强度的重要指标之一。考虑混合多馈入系统中柔性直流系统（VSC-HVDC）对短路比指标计算的影响，基于短路比的定义，本文分别从短路容量和等效直流功率两方面出发，分析VSC-HVDC对系统短路电流及多馈入相互作用因子的影响，进而提出一种计及柔性直流的混合多馈入系统短路比指标计算方法。最后通过对混合多馈入直流系统模型和实际大系统的仿真，验证了这一方法在计算含柔性直流系统的短路比时具有准确性。

短路比；多馈入交互作用因子；VSC-HVDC；交流电网强度；电力系统稳定

0 引言

基于电网换相换流器的高压直流输电技术（line commutated converter based high voltage direct current, LCC-HVDC）凭借其输送距离远、输送容量大等优点已成为我国大电网异步互联的重要方 式[1]，但其稳定运行需要有一定强度的受端交流电网提供电压支撑。基于电压源换流器的柔性直流输电技术（voltage source converter based high voltage direct current, VSC-HVDC）不存在无功补偿不足、换相失败等问题，且具有同时独立调节有功功率和无功功率等优点[2]，在近几年得到了广泛关注和应用[3-4]。目前，已有不少工程将柔性直流馈入原有的传统交直流输电线路中形成混合多馈入系统。柔直馈入将会对电网潮流分布[5-6]、功率传输[7]等产生多方面的作用，进而影响系统运行的稳定性。

系统的运行特性与其所连接的受端交流电网电压支撑能力关系密切，目前普遍应用基于电网结构参数的短路比（short circuit ratio, SCR）指标对受端电网强度进行评估[8]。对于单馈入系统，由短路比的概念进一步衍生出有效短路比[9]、综合短路比[10]等。对于多馈入直流系统，学术界定义了多馈入短路比及有效短路比[11]概念，进而又衍生出多馈入直流系统广义短路比[12]等。

然而，上述短路比指标均是基于LCC-HVDC系统提出的，VSC-HVDC和LCC-HVDC在运行特性和控制方式上有很大的不同，因此这一指标并没有考虑柔直馈入后对计算结果可能产生的影响。目前，不少文献针对含柔性直流的混合多馈入系统短路比进行了相关研究。文献[13-14]认为VSC-HVDC对受端电网的影响作用与其运行方式和接入地点密切相关，即改变多馈入交互作用因子（multi-infeed interaction factor, MIIF）以影响系统短路比，但未能考虑VSC-HVDC馈入对短路容量的影响。文献[15]以LCC-HVDC功率曲线相同为原则将混合双馈入系统等效为传统单馈入系统，并认为等效后的系统短路比可用于衡量等效前的混合双馈入系统的受端电网强度，但这一等效过程随机性较大。文献[16]将混合双馈入系统等效为具有相同电动势和交流系统阻抗的传统单馈入系统，提出了等效有效短路比的定义，但这一指标的应用背景局限于混合双馈入系统。

为考虑短路比在含柔性直流的混合多馈入系统中的计算问题，研究VSC-HVDC对LCC-HVDC所连接的受端电网强度的影响，本文基于短路比的定义，从短路容量和等效直流功率两方面出发，分析柔直对系统短路电流及各直流系统间MIIF的影响，并提出一种计及柔直的多馈入短路比指标计算方法。最后分别在混合多馈入系统和某网大系统中进行仿真，仿真结果验证了所提方法的准确性。

1 短路比指标

短路比定义为

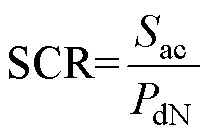
式中：ac为直流系统换流母线的短路容量；dN为直流系统额定容量。

对于多馈入直流系统，计算短路比时通常将系统简化为一个等效模型进行求解，如图1所示。

此时多馈入系统短路比定义为[11]

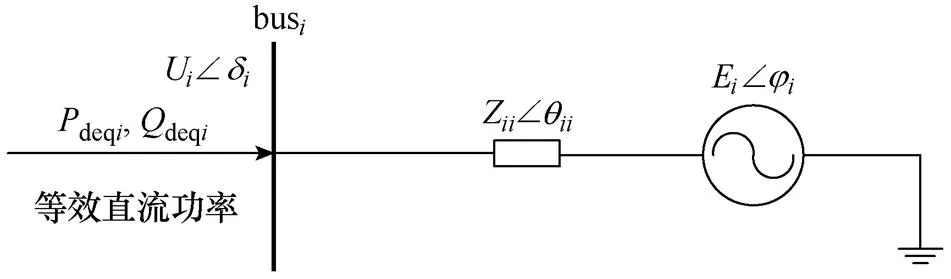
图1 多馈入系统的等效模型

式中：deqi为所有直流系统等效注入换流母线的功率；Z为等效交流系统阻抗；Z为换流母线和之间的互阻抗；为系统数。

MIIF是用于衡量各直流换流站之间电压相互作用程度的指标，其定义为：当换流母线上投入对称三相电抗器，使该母线的电压变化量为1%时，换流母线上的电压变化率[14]。当忽略电力系统元件外特性影响并假设各节点电压幅值和相位相等时，MIIF可简化计算为[17]

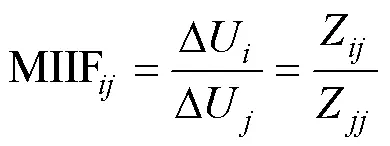
在这一条件下，式（2）可进一步表示为

由上述分析可知，无论是短路比还是多馈入短路比，从数学形式上来看都是受端系统的短路容量与直流功率的比值。

2 VSC-HVDC对LCC-HVDC馈入点短路比的影响

图2为混合多馈入系统简化模型，其中，有个LCC-HVDC、-个VSC-HVDC馈入交流电网。di、di为各直流系统注入换流母线的有功功率和无功功率；ci、ci为LCC-HVDC的补偿电容和补偿无功功率；UÐ为各换流母线电压相量；ZÐ、EÐ分别为各交流系统的等效阻抗和等效电动势；LinÐLin为LCC-HVDC与VSC-HVDC系统间联络线阻抗。

2.1 对短路容量的影响

在计算多馈入短路比时，短路容量ac可通过式（5）获得，即

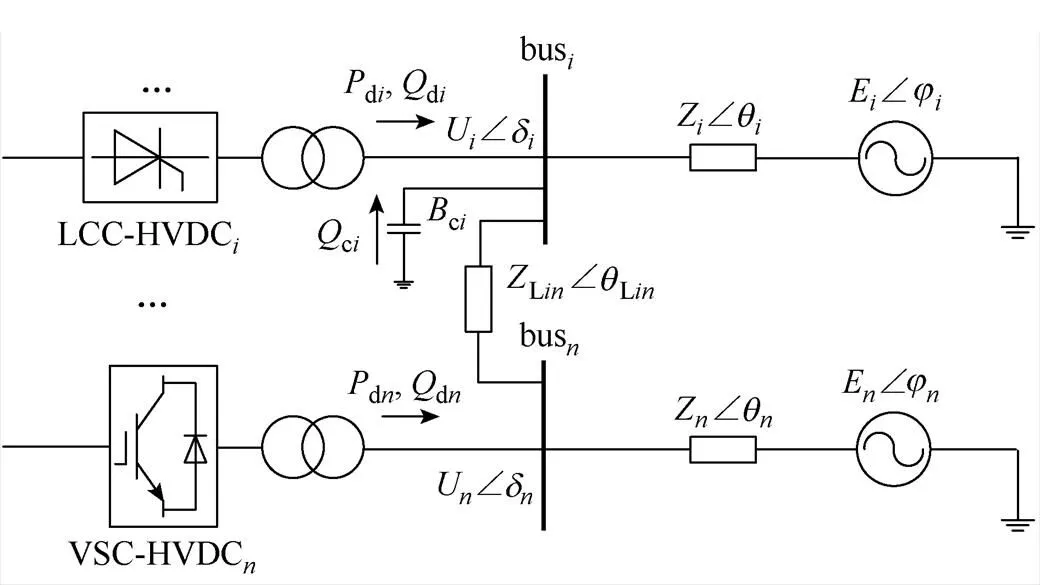
图2 混合多馈入系统简化模型

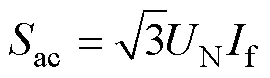
式中：N为直流系统换流母线的额定电压；f为直流系统换流母线三相金属性接地时的短路电流。对于换流母线，当发生三相金属性接地短路时，边界条件为

式中：f(1)、fi(2)、fi(0)分别为交流系统作用下故障点f的正序、负序和零序电压，即短路点电压仅包含正序分量；acfi(1)、acfi(2)、acfi(0)分别为交流系统在各序网络中形成的短路电流；fi(1)为短路点f的接地电阻，此时fi(1)=0。换流母线发生三相金属性接地短路时，除短路点f以外的系统仍然对称，传统电源仅提供正序电势aci(1)[18]，因此有

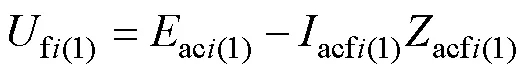
式中：acfi(1)为正序网络中受端交流系统到短路点f的阻抗，包括系统间的联络母线阻抗。由于acfi(2)=acfi(0)=0，故交流系统提供的短路电流为

对于LCC-HVDC，由于交流侧发生短路时逆变站换流器换相失败导致闭锁，且本文主要研究VSC- HVDC对系统短路比的影响，因此暂不考虑LCC- HVDC对短路电流的贡献。

对于VSC-HVDC，由于其换流器采用全控型器件，不存在换相失败的问题，且常采用直接电流控制策略，即通过PI调节器对电流内环和电压、功率外环控制进行串联校正。内环电流控制器根据外环传递而来的参考电流，对dq轴上的电流限幅实现VSC交流侧电压幅值和相位的直接控制[19]，因此可将柔直当作受控电流源处理。利用Park逆变换将VSC-HVDC在dq轴上体现的电流源特性转换到三相坐标系中表示为

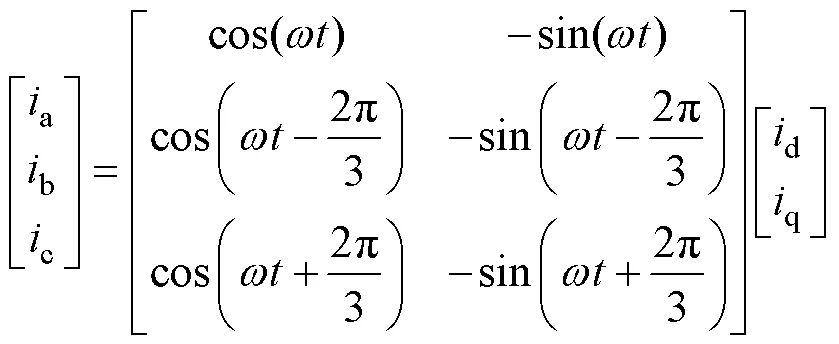
式中，、分别为角频率和时间。

由于分析交流系统提供的短路电流分量时采用三序电流表示，故以a相为例，利用对称分量法将式（9）进一步变换得到三序分量，即

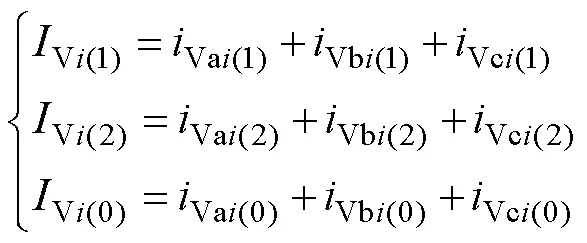
式中：=j120°；Vi(1)、Vi(2)、Vi(0)分别为VSC换流器等效的正序、负序和零序受控电流源。等效后的VSC换流器三序等效网络如图3所示，此时VSC贡献的短路电流dcfi由式（12）计算得到。

图3 VSC换流器的三序等效网络

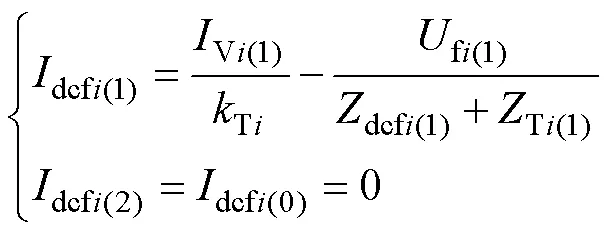
式中：dcfi(1)、dcfi(2)、dcfi(0)分别为VSC-HVDC贡献的三序短路电流，由于三相接地短路，所以短路电流不存在负序和零序分量；dcfi(1)为VSC换流器到短路点f的正序阻抗，包括系统间的联络母线阻抗；Ti(1)为正序的换流器阻抗，主要包括换流变和等效桥臂的阻抗；Ti为VSC换流变电压比。

因此，当换流母线发生三相短路时，计及VSC-HVDC的短路电流f表示为

需要注意的是，此处的短路电流选取的是短路瞬间周期分量初始值，由于VSC换流器在不同控制方式下对短路电流的影响主要体现在稳态值上，且对于发生在LCC-HVDC馈入的受端交流系统的三相短路，由式（13）可知VSC换流器贡献的短路电流会受到换流站器件和网络结构参数影响，可以推断VSC换流器在不同控制方式下对短路电流的影响不大。

2.2 对等效直流功率的影响

由式（2）可知，在传统多馈入系统中第个LCC-HVDC的等效直流功率可以表示为

可以认为混合多馈入系统与传统多馈入系统在等效直流功率上的差异取决于MIIF。文献[20]推导出了在传统多馈入系统下考虑直流系统控制方式的MIIF表达式为

式中：U、Q分别为换流母线的电压及与之相连的等效直流系统注入换流母线的无功功率；Z、Z分别为节点、的自阻抗；Z为节点、间的互阻抗；dQ/dU为母线上的无功-电压特性。VSC- HVDC逆变站处于不同控制方式时，对MIIF的影响主要从dQ/dU体现，因此式（15）同样可以推广到混合多馈入系统中，此时可将dQ/dU分为两部分，即

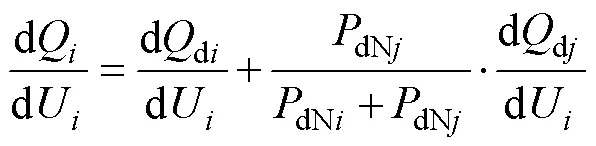
式中：ddi/dU和ddj/dU分别为直流系统在各自容量基准下计算得到的无功-电压特性。此处主要考虑换流母线连接的VSC-HVDC、换流母线连接的LCC-HVDC情况（下文同）：若VSC逆变站处于定交流电压控制，在小扰动下交流电压U维持不变，此时dQ/dU=∞，故MIIF=0，计算等效直流功率时将不考虑柔直的直流功率分量；若VSC逆变站处于定无功功率控制，ddi/dU=0，此时dQ/dU变小，

通过上述分析，可以得到混合多馈入系统中计及柔直的短路比指标计算方法为

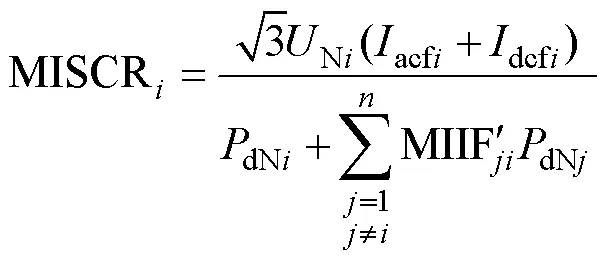
3 案例验证

3.1 多馈入系统模型仿真

由前述可知，VSC-HVDC主要通过改变系统的短路电流和MIIF来影响系统的短路比计算。本节通过在PSCAD/EMTDC中对混合多馈入系统进行仿真分析，研究计及柔直对短路比计算的影响，并验证所得短路比计算方法的准确性。

建立如图4所示的仿真模型，案例1为VSC- HVDC逆变侧处于定有功功率和定无功功率控制的混合多馈入系统，案例2为VSC-HVDC逆变侧处于定有功功率和定交流电压控制的混合多馈入系统。不计及柔直情况即将VSC换流站当作LCC换流站处理。LCC-HVDC系统参数见标准CIGRE模型，整流站和逆变站均分别处于定直流电流和定熄弧角控制。1=2=3=0.236p.u.，L12=0.463p.u.，L13=0.555p.u.，L23=0.648p.u.，其他参数见表1。

分别于换流母线1、2处发生三相金属接地故障，并测量获取VSC换流器电流内环限幅数值。各案例下的短路电流见表2。受网络阻抗影响，整体而言混合多馈入系统中VSC-HVDC逆变侧不同控制方式对系统短路电流产生的影响差别不大，但计及柔直情况下的案例1和案例2短路电流均大于不计及柔直情况，说明VSC-HVDC确实贡献了部分短路电流，与2.1节分析一致。

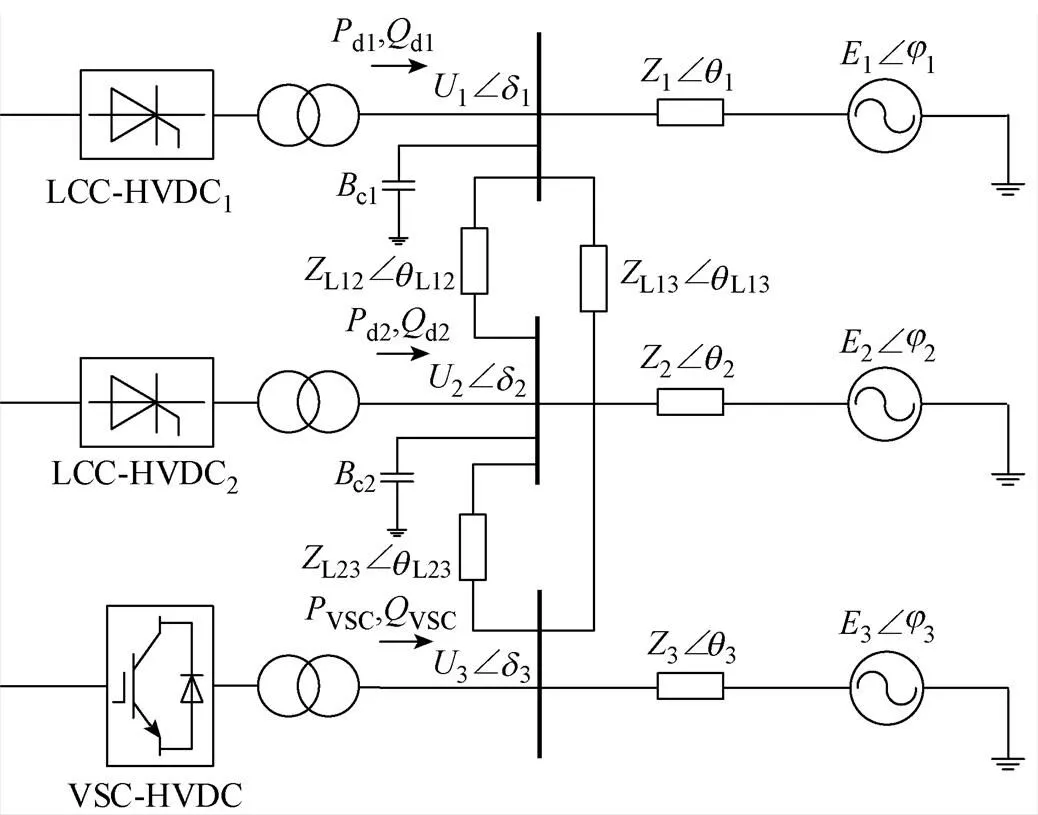
图4 混合三馈入直流系统简化模型

表1 系统模型主要参数

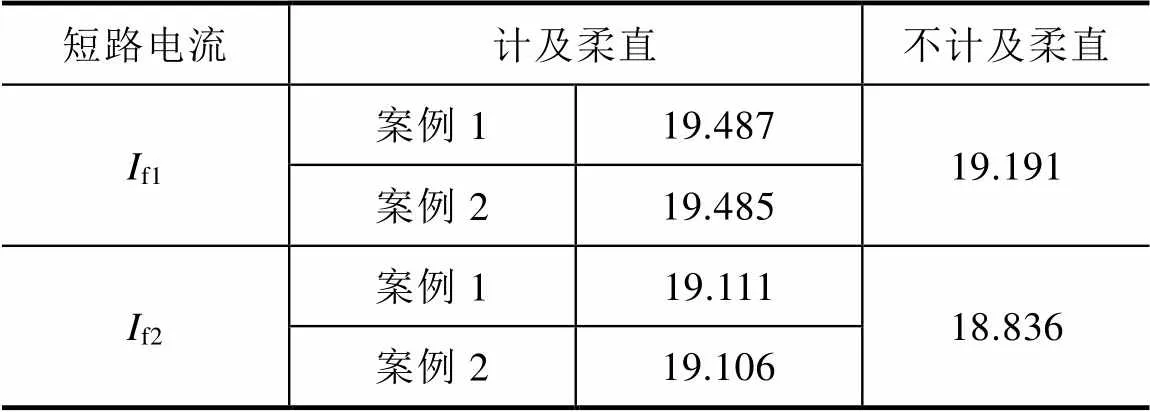
表2 各案例下的短路电流 单位: kA

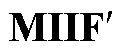
表3 各案例下的部分

表4为各案例下LCC-HVDC1和LCC-HVDC2的多馈入短路比情况。计及柔直情况下的案例1和案例2的多馈入短路比均大于不计及柔直情况，同时验证了目前学术界中VSC-HVDC馈入对系统短路比具有提升作用、改善系统稳定性的观点。

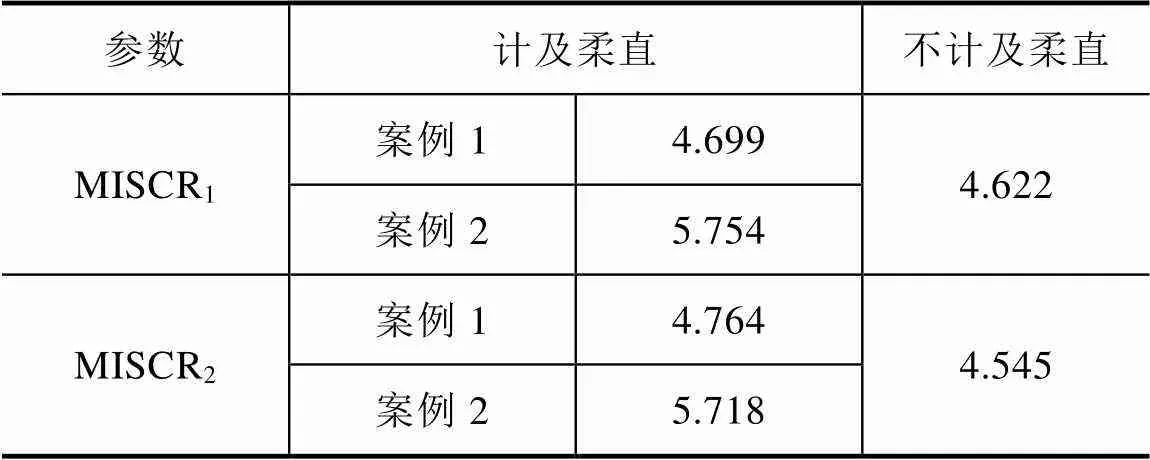
表4 各案例下的多馈入短路比

3.2 大系统仿真

为更切合实际工程，本节基于某电网某年夏大方式BPA模型进行仿真分析。比较某直流工程逆变站（下称GD08）采用柔性直流方式馈入电网时其他直流逆变站的多馈入短路比及相关量的情况。案例3为GD08逆变站采用定无功功率控制，案例4为GD08逆变侧采用定交流电压控制，不计及柔直时GD08以传统直流方式馈入电网。下面选取电网中主要4个LCC直流逆变站进行分析，结合相关功能卡获取的仿真数据进行处理得到的结果见表5～ 表7。

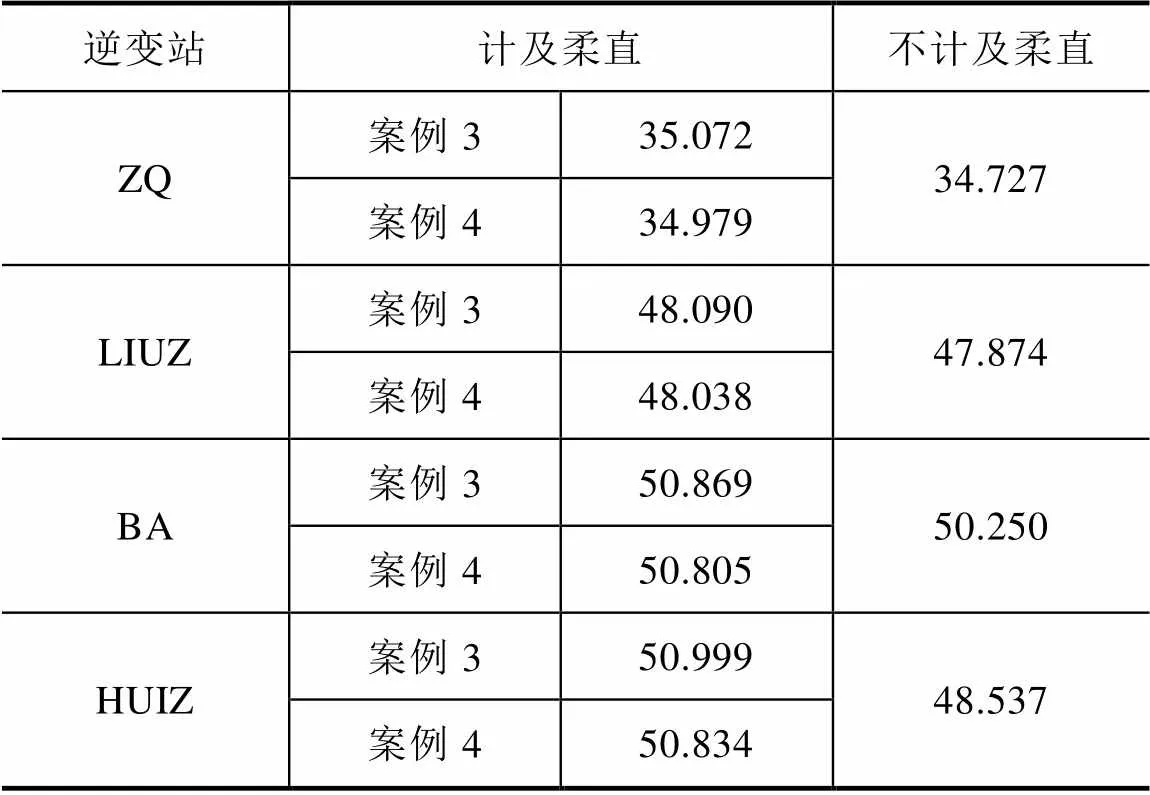
表5 各直流逆变站短路电流 单位: kA

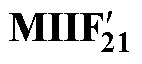
表6 部分直流换流站间

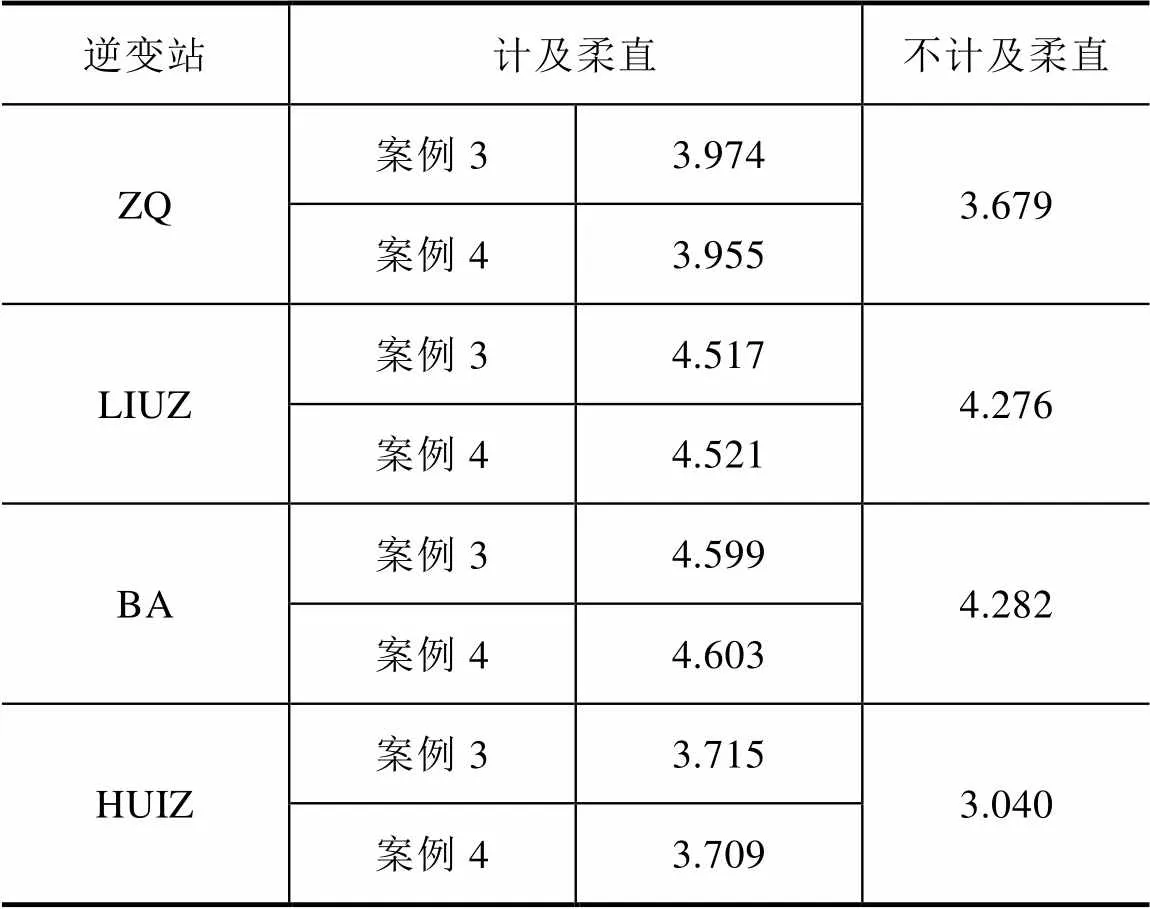
表7 部分直流逆变站多馈入短路比

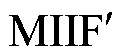
分析表7可知，计及柔直时各直流逆变站的多馈入短路比均大于不计及柔直情况，且二者数值相差较大，说明此时柔直对短路比的影响已不能再忽略。

4 结论

基于短路比的定义，本文从短路容量和等效直流功率两方面出发，分析了柔直馈入对系统的影响，并得到了计及柔直的短路比指标计算方法。主要结论如下：

1）混合多馈入系统中，VSC-HVDC会贡献部分短路电流，且这一短路电流分量受VSC换流器阻抗和系统阻抗影响。

2）VSC-HVDC逆变侧处于定交流电压控制时，与其相关的MIIF为0；VSC-HVDC逆变侧处于定无功功率控制时，MIIF变小。

3）通过多馈入直流系统和大系统的仿真验证了所得计算方法的实用性。计及柔直的混合多馈入系统短路比通常大于不计及柔直的情况，必要时需对这一变化情况多加考虑，并进一步从数值上验证了柔直的馈入增强了系统受端电网强度、改善了系统稳定性的结论。

[1] 赵畹君. 高压直流输电工程技术[M]. 2版. 北京: 中国电力出版社, 2011.

[2] 徐政, 屠卿瑞, 管敏渊, 等. 柔性直流输电系统[M]. 北京: 机械工业出版社, 2012.

[3] 邹焕雄, 李超, 胡文旺, 等. 厦门柔性直流输电工程真双极大功率试验方法研究[J]. 电气技术, 2017, 18(6): 23-26, 33.

[4] 赵岩, 郑斌毅, 贺之渊, 等. 南汇柔性直流输电示范工程的控制方式和运行性能[J]. 南方电网技术, 2012, 6(6): 6-10.

[5] 王浩翔, 赵冬梅, 陶然, 等. 基于分解的多目标进化算法的含MMC-HVDC交直流混合系统最优潮流研究[J]. 电工技术学报, 2020, 35(17): 3691-3702.

[6] 王紫瑶, 廖进贤, 杨家豪, 等. 计及功率控制模式的VSC-MTDC交直流并列运行系统概率潮流计算[J]. 电气技术, 2019, 20(2): 12-17.

[7] 丁海龙, 袁志昌, 吴爱军, 等. 混合双馈入直流系统最大传输功率控制策略研究[J]. 电工技术学报, 2020, 35(2): 330-336.

[8] IEEE guide for planning DC links terminating at AC locations having low short-circuit capacities: IEEE Standard 1204—1997[S]. New York: IEEE, 1997.

[9] 徐政, 黄弘扬, 周煜智. 描述交直流并列系统电网结构品质的3种宏观指标[J]. 中国电机工程学报, 2013, 33(4): 1-7.

[10] 肖浩, 李银红, 段献忠, 等. 计及LCC-HVDC交直流系统静态电压稳定的综合短路比强度指标[J]. 中国电机工程学报, 2017, 37(14): 4008-4017.

[11] DAVIES J B. Systems with multiple DC infeed[J]. Electra, 2007(233): 14-19.

[12] 辛焕海, 章枫, 于洋, 等. 多馈入直流系统广义短路比: 定义与理论分析[J]. 中国电机工程学报, 2016, 36(3): 633-647.

[13] 何英静, 李继红, 但扬清, 等. 柔性直流输电系统对多直流馈入系统运行性能的改善作用研究[J]. 电力电容器与无功补偿, 2020, 41(3): 106-111.

[14] CIGRE Working Group B4. 41. Systems with multiple DC infeed[R]. Paris, France: CIGRE, 2008.

[15] AIK D L H, ANDERSSON G. Impact of renewable energy sources on steady-state stability of weak AC/DC systems[J]. CSEE Journal of Power & Energy Systems, 2017, 3(4): 419-430.

[16] 田宝烨, 袁志昌, 余昕越, 等. 混合双馈入系统中VSC-HVDC对LCC-HVDC受端电网强度的影响[J]. 中国电机工程学报, 2019, 39(12): 3443-3454.

[17] 林伟芳, 汤涌, 卜广全. 多馈入交直流系统短路比的定义和应用[J]. 中国电机工程学报, 2008, 28(31): 1-8.

[18] 易杨, 沈豫, 林章岁. 柔性直流输电系统贡献交流短路电流的特性分析及计算方法[J]. 高电压技术, 2018, 44(7): 2150-2158.

[19] 卜广全, 李英彪, 王姗姗, 等. MMC对交流系统三相短路故障短路电流影响的机理研究[J]. 中国电机工程学报, 2017, 37(21): 6303-6312.

[20] 夏成军, 王真, 杜兆斌. 考虑直流系统控制方式的多馈入交互作用因子实用计算方法[J]. 电网技术, 2017, 41(11): 3532-3538.

Research on short circuit ratio index considering VSC-HVDC systems

HUANG Chuyin1,2XIA Chengjun1,2ZHONG Mingming1,2

(1. School of Electric Power Engineering, South China University of Technology, Guangzhou 510640;2. Guangdong Provincial Key Laboratory of Intelligent Operation and Control for New Energy Power System, Guangzhou 510663)

The operating characteristics of power system are closely related to the strength of the receiver AC network, and the short-circuit ratio based on the conventional DC system is one of the important indicators to measure the strength of the receiver AC network. In order to consider the influence of VSC-HVDC in hybrid multi-feed system on the calculation of short-circuit ratio index, based on the definition of short circuit ratio, this paper studies the relationship between VSC-HVDC and short circuit current and multi-feed interaction factor from two aspects of short-circuit capacity and equivalent DC power, respectively. Furthermore, a method for calculating the short-circuit ratio index of the hybrid multi-infeed system considering VSC-HVDC is proposed. Finally, the accuracy of this method in calculating the short-circuit ratio of the system with VSC-HVDC is verified by the simulation of the multi-feed DC system model and the actual large system.

short circuit ratio; multi-infeed interaction factor; VSC-HVDC; AC system strength; power system stability

2021-08-30

2021-09-09

黄楚茵（1997—），女，广西贵港人，硕士研究生，主要研究方向为柔性直流输电的稳定性分析。

国家自然科学基金委员会-国家电网公司智能电网联合基金资助项目（U1766213）