变时滞反馈散料加工系统的参数设计

2022-03-27张红兵李万祥李雄兵

振动与冲击 2022年6期

陈宁，张红兵，李万祥，李雄兵

(兰州交通大学机电工程学院，兰州 730070)

散料加工机械中普遍利用料斗作为散料的临时储存设备，但是大多数的料斗下缺乏散料供给速度控制机构，散料的供给速度和消耗速度无法达到动态平衡，一般情况下导致原料的堆积，影响设备的生产效率。魏放等[1]通过模拟仿真研究，验证了供料速度的增加降低筛分加工效率的可能性，筛面的大量物料堆积将降低振动筛的抛掷指数，而振动筛的抛掷指数是决定筛分加工速率的关键因素之一[2]。

利用控制系统对原料供给速度进行反馈调节控制是一种有效的解决方案，然而引入反馈控制环节意味着系统状态参数之间的相互耦合性更强，系统的动力学行为更加明显，如自激振动的发生[3]。在设备工作时，稳定的运动状态是被期望的，一旦系统发生Hopf分叉，意味着系统的平衡状态失稳。

当前的学术研究中，关于非时滞系统被动控制理论极为成熟，时滞系统尤其变时滞系统的控制稳定性相关工作较少，导致了变时滞系统的被动控制参数设计中可借鉴的依据方法比较少。

时滞是自然界和社会中普遍存在的现象，虽然其中有些延迟的程度极低，直到可以被忽略的程度，但是客观存在的时滞现象是系统动力学研究中需要考虑的非线性因素[4]。如机械成型中的再生切削效应[5-6]、病毒的感染延迟传播[7-9]、食物链中的扑食延迟[10]、以及反应扩散等[11]。其次时滞也被大量用于机械、电子等系统的稳定性控制[12-13]和人工智能等领域[14-15]，可见时滞对系统动力学不可忽视的影响。

目前对含时滞系统的研究主要针对在系统的稳定性分析和主动控制中的应用。稳定性分析的关键为对Hopf分叉的研究，研究时滞动力系统稳定性主要有两类方法, 一类是基于Lyapunov函数/泛函方法；另一类是基于系统方程的特征根进行分析的方法[16]，其中采用特征多项式分析的案例较多。如在文献[6-11,14-15]中均采用分析特征方程的方法研究时滞系统的Hopf分叉，其中文献[9,11]中采取该方法分别对双时滞和三时滞系统的Hopf分叉进行了一定的研究。其分析过程对理论水平和专业性的需求较强，需要做出大量的分类讨论，得出特定结论的条件约束性较强，可普及性较差。

本文主要针对变时滞被动控制系统的参数设计展开研究，在部分参数被约束或者确定的条件前提下，期望确定其他参数的可选择区间和范围，继而为设计工作提供理论和方法。

1 模型建立

系统模型如图1所示，图1中：A为给料模块出料口;P为散料供给速度；受到加工模块沉降信号Y的反馈调节，控制环节增益系数为α；物料从料口处自由落体至加工单元的时间为τ;定义加工单元接受的实时流量P(t-τ)为原料接收速度；B为加工模块;M为加工单元中待处理的堆积原料质量；N为加工模块的净质量；Q为原料加工速度即堆积物料的消耗速度;加工模块中的物料堆积会影响加工速度，相关比例系数为β;K为加工模块支撑弹簧的刚度系数；C为系统配置的阻尼器阻尼系数；H为下料单元和加工单元的初始静态高度差;Y为加工单元的垂向位移。重力加速度为G，t为系统的参考时间。

图1 散料加工系统示意图

该系统中，当堆积质量M>0时，堆积质量M的增加会导致处理速度Q的降低，当堆积质量为M=0时，处理速度将受到物料接收速度P(t-τ)的影响，此时需要满足加工速度不大于受料速度，处理速度约束关系的表达式见式(1)。

(1)

在本文所有式(1)～式(30)中，在圆括号内的参数表示函数或者状态变量的自变量，圆括号部分不参与乘法运算。

在系统中堆积质量M由物料接受速度P(t-τ)和处理速度Q的共同影响，表达式见式(2)。

(2)

如果原料供给速度P缺乏控制，极可能会导致堆积质量的持续增加，产生大量的物料堆积，形成恶性循环，最终降低系统的生产效率。

在此利用加工单元的垂向位移Y作为控制信号，反馈控制原料供给速度P，从而使系统保持稳定状态，料斗出口端的流量表达式如式(3)所示。物料经过时间延迟τ之后，作用在加工单元质量N上，并造成一定的冲击力Fp。假设冲击过程符合完全非弹性碰撞和动量冲量定理，可求得物料对加工单元质量N的实时冲击力Fp，冲击力Fp的表达式为式(4),以及时间延迟τ的表达式为式(5)。

P(t)=max(P0-αY(t),0)

(3)

(4)

(5)

根据牛顿第二定律和式(2),可以求得系统的动力学微分方程表达式如式(6)所示。

(6)

代入式(4)，可以将式(6)降阶为状态微分方程式(7)，其中变量P和τ是关于状态变量Y的表达式，具体关系见表达式(3)、式(5)。

(7)

(8)

(9)

(10)

2 稳定性分析

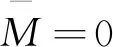
(11)

(12)

(13)

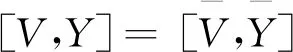
det(J-λI)=

(14)

在此假设其特征值形式为式(15)并代入式(14),分离虚实部分别可得式(16)和式(17)。

λ=ωi+υ

(15)

(16)

(17)

联解式(16)、式(17)可得到参数[K,C]关于参数[υ,ω]的显性解析表达式(18)、式(19)。

(18)

(19)

代入发生Hopf分叉的临界条件为υ=0则可以得到发生Hopf分叉时刚度K和阻尼C关于参数ω的参数表达式。将已知的参数[υ，ω,K,C]代入式(16)、式(17),对[K,C](υ,ω)求关于υ的偏导数，并将各参数代入表达式，利用反函数的求导法则容易求得参数[K,C]对υ的导数。代入Hopf分叉的条件，则可以确定能使系统稳定的参数所在的区间，或者结合式(16)、式(17)亦可得到相同的结果。

(21)

然后利用如式(22)所示的参数转化,可实现表达式(21)向表达式(23)的简化。

(22)

-p3det(J-λI)=p3λ3+p2λ2-τCλ2+p1λ+

(23)

将式(15)的特征值形式代入式(23)并分解虚实部可分别得到实部平衡式(24)和虚部平衡式(25)。

(26)

p0+R1p1+R2p2+R3P3+Rλ=0

(27)

I1p1+I2p2+I3P3+Iλ=0

(28)

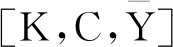
(29)

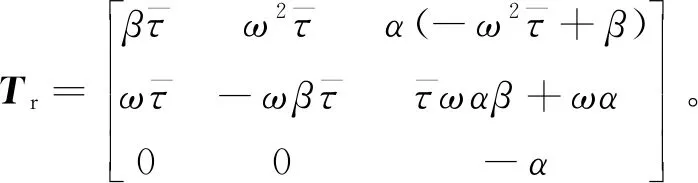
(30)

式中

3 算例分析及验证

在完成理论的基础上，接着对理论分析的正确性和合理性做出仿真验证，采取理论成熟可靠的SIMULINK软件仿真平台进行理论方法验证，建立系统的数学模型方程式(7)所对应的SIMULINK软件仿真框图模型如图2所示。

图2 系统的SIMULINK模型

在系统各参数的期望值附近取带量纲算例参数P0=200 kg/s、α=20 (kg/s)/m、β=0.1 (kg/s)/kg、Q0=200 kg/s、G=10 m/s2、N=2 000 kg。求得有效的临界稳定参数区域的边界曲线如图3所示，当参数[K,C]坐标在图中曲线上时，系统将发生Hopf分叉，系统处于临界稳定状态。

图3 临界稳定条件

图3中反映出，系统保持临界稳定状态的参数[K,C]组合中，一个刚度系数K最多可以和两个阻尼参数匹配，在某些参数下，这样的匹配关系无法成立，如τ=0.1 s、K=2 200 N/m时。但是一个阻尼参数至少和一个刚度参数相匹配，甚至可以和3个刚度系数相匹配，说明在参数的选择上，刚度系数的选择要比阻尼系数更为苛刻。在该系统中刚度可以决定平衡点的位置，阻尼可以决定系统的稳定性。

下面分别就存在临界阻尼系数和不存在临界阻尼系数的参数组合情况分别进行验证。

3.1 有分叉解的算例验证

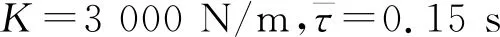
C1=46.295 72 N/(m/s),ω1=0.903 915 rad/s

C2=168 33.96 N/(m/s),ω2=0.039 656 rad/s

目前，吸入性糖皮质激素在慢性阻塞性肺疾病治疗中应用广泛。有研究证实，吸入性糖皮质激素可降低慢性阻塞性肺疾病急性加重期发生率[30]。吸入性糖皮质激素具备强大抗感染作用，其抗感染机制包括抑制细胞膜磷脂释放花生四希酸，从而减少炎症介质白三烯、前列腺素的合成，抑制炎症细胞活化与迁移，进而减少细胞因子生成。同时，吸入性糖皮质激素可增加慢性阻塞性肺疾病患者患者气道平滑肌对β2受体激动剂的反应性，预防气道重塑，减少血管渗出，缓解水肿，减轻患者炎症病变、气道堵塞感。

利用反函数的求导规则可知

因此当C∈(C1,C2)时，必定有υ≤0，说明阻尼系数在该区间时系统能够保持稳定。通过模拟仿真得到系统参数C分别在C1和C2附近取值时的时间历程图,如图4和图5所示。

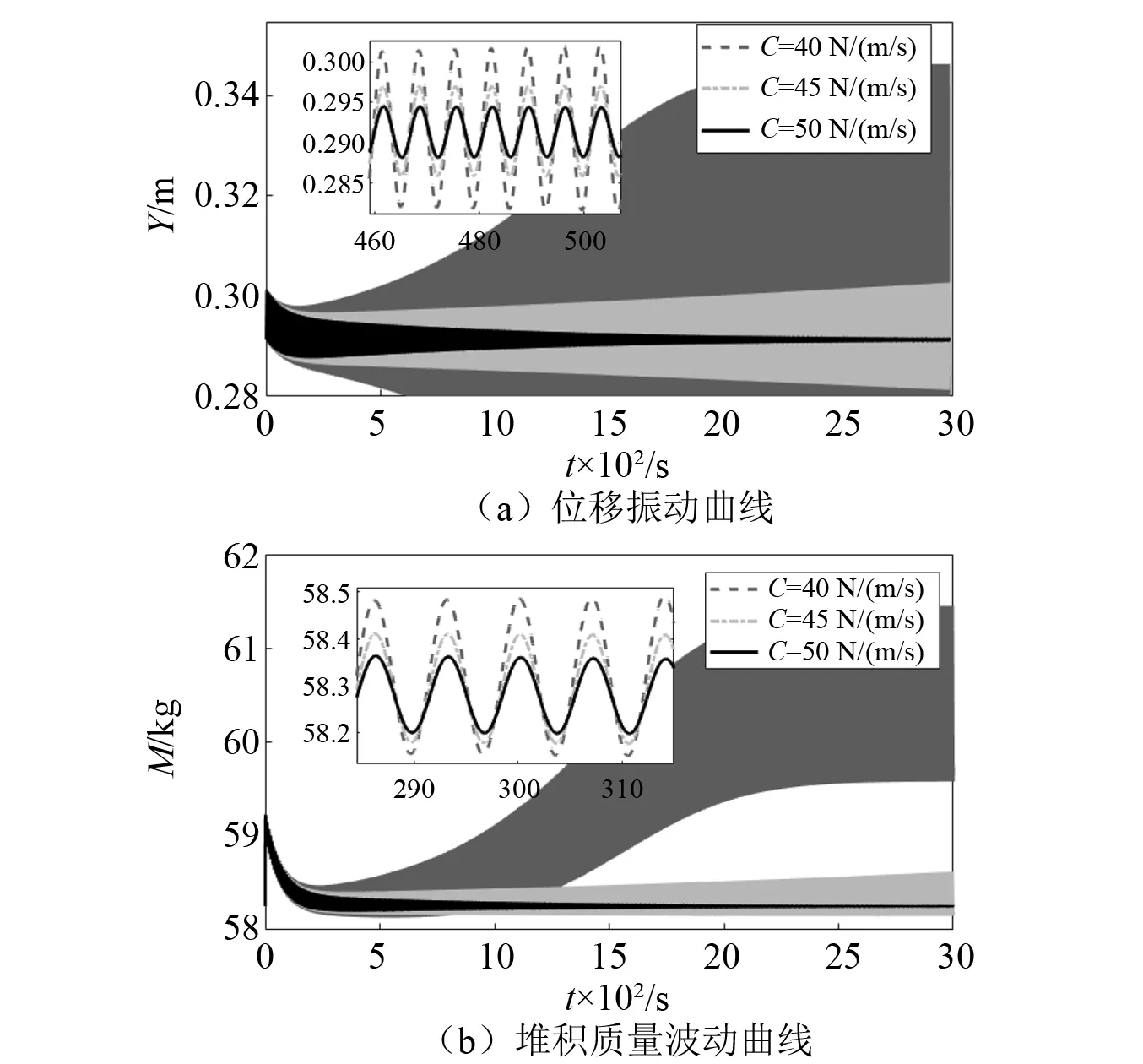
图4 C=U(C1,5)时的时间历程图

图5 C=U(C2)时间历程图

从图4中可以看出，当C=40 N/(m/s)时，系统的瞬态振动发散，衰减指数大于零；当C=45 N/(m/s)时，系统的衰减指数接近零；当C=50 N/(m/s)时,系统的瞬态振动收敛。在C1的邻域U(C1,5)内，随着参数C的增大，自激振动衰减指数从正数递减至负数，说明该邻域内存在一个衰减指数为零的点。

从图5中可以看出，当C=16 750 N/(m/s)时，系统的瞬态振动收敛，衰减指数小于零，系统给能够保持稳定；C=16 834 N/(m/s)时，系统的衰减指数接近零；当C=16 900 N/(m/s)时,系统的瞬态振动逐渐发散。在C2的领域U(C2,80)内，随着参数C的增大，自激振动衰减指数从负数增加至正数，说明在该邻域内必定也存在一个衰减指数为零的点。

3.2 无分叉解的算例验证

图6 K=2 200 N/m时间历程图

当C=10 N/(m/s)时，系统具有簇发性周期振动的特点，当C=100 N/(m/s)时，系统的主要振动为周期运动，当C=1 000 N/(m/s)时，系统运动显示为多周期运动，当C=10 000 N/(m/s)时，系统运动具有周期性。

3.3 抗干扰能力仿真验证

通过对图2分析可知，稳定状态时滞越小，其参数的稳定区间越小，且在特定的刚度区间可能存在无解的状态。同时可以发现刚度参数取K>2 500 N/m时，阻尼参数已经具有较大的可取范围。在此取K=3 000 N/s，C=3 000 N/(m/s)，利用随机激励给系统施加一定的激扰，检验系统的抗干扰能力。

考虑系统的特点，散体的落料过程的激扰主要为孔隙导致的质量流量波动。在此对理想的原料供给速度P0按一定的百分比施加随机激励，仿真时间历程图如图7所示，可见该参数下对20%内的原料供给速度波动具有抑制作用，并保持系统在设计的稳定点附近工作。

图7 随机激励下稳定运动

其次通过前面的分析可知，在参数H和K已知的情况下，系统中最多可存在三重解，当系统受到扰动，并超出设计平衡点所对应的吸引域时，亦可能会导致系统跳出当前的吸引域从而转移至其他平衡点。如图8所示，当随机激励强度为25%时，系统状态从设计期望的工作状态失稳迁移至其他的平衡点处。同样，在实际情况中，虽然由于弹簧的硬性特征和截断特征，不会出现达到10 m的状态跃迁，但是足以说明这种强度激扰下原Y=0.29 m的平衡点失稳的必然性。在此给出20%的扰动量已经远高于一般工业现场情况，说明了选取的参数具备较大的调节能力。