基于神经网络的短电弧覆盖次数最优化模型研究
2022-03-27范凯旋商庆清
李 杰, 孙 炜, 范凯旋, 商庆清
(南京林业大学机械电子工程学院,江苏 南京 210037)
1 研究背景
短电弧加工是指在具有一定气、液比例且带压力的混合物工作介质的作用下,利用两个电极之间产生的受激发短电弧放电群组或混合有火花放电的放电群组,来蚀除金属或非金属导电材料的一种电加工方法,是一种新型的强焰流、电子流、离子流、弧流混合放电加工方法,属于特种加工行业电加工技术范畴。
短电弧加工技术主要用于加工各类水泥磨辊、立磨辊、渣浆泵叶轮、大型冷轧工作辊、高速线材辊及其他大型工件上的高强度、高硬度的难加工金属材料,如电焊、等离子堆焊后的表面金属材料,可以高效率地对此类大型磨辊、轧辊外圆表面进行修复、再制造加工[1]。
作为一种大功率高效电加工方法,短电弧加工过程中峰值电流可达上千安培,消耗大量热量与能量,其间伴随的能量损耗不容忽视,这些能耗也会引起电源整机温度上升,降低电源内部元器件的使用寿命,影响电源整机稳定性,会对整个短电弧加工过程产生很大影响。因此,研究最少短电弧放电次数模型是发展短电弧技术的关键[2]。
1.1 问题引出
当使用半径为60.5 mm的球形短电弧对半径为1 000 mm的圆形材料实现完全覆盖,且短电弧加工所形成的球形电弧的球心落在待蚀除金属或非金属导电材料的平面上时,此问题可以转化为求解平面问题,即使用半径为r的小圆对半径为R的大圆区域实现完全覆盖时,采用何种方式能够使半径为r的小圆个数最少,此处r=60.5 mm,R=1 000 mm。
多个圆形之间的密排方式有相切与相交两种,其中,以相切的方式进行密排必然会导致出现间隙;因此,本文研究的问题转化为小圆之间以何种方式相交时,能够令小圆使用个数最小,同时实现对大圆的完全覆盖。多个圆形相交时,产生的交点之间的连线能够形成圆的内接封闭多边形;而当多个大小相同的圆形相交时,其交点之间的连线所形成的多边形为正多边形时,能够使圆形之间因相交产生的重复覆盖面积达到最小。
1.2 六边形覆盖模型
在已知二维平面的覆盖问题上,利用正n边形覆盖特定区域且要求使用正n边形的个数最少,需要满足x个正n边形的顶点都位于同一个点上,使得恰好能拼接成360°的一个圆周。由于正n边的内角度数为:
(1)
所以在一个顶点处的x个正n边形应满足方程:
(2)
解得:
(3)
其中x必须为整数,则其解只有以下几种情况:
n=3,x=6
n=4,x=4
n=6,x=3
(4)
由以上解可以得出,当小圆交点连线形成的封闭多边形为正三角形、正方形、正六边形时,顶点都位于同一个点上,使得恰好能拼接成360°的一个圆周,3种情况示意图如图1所示。

图1 3种情况示意图
使用相同大小的圆相交,使每个小圆内的交点分别连接成小圆的内接正三角形、正方形和正六边形,此时相邻两个小圆的重叠面积占整个圆面积的占比为:
(5)
当n=3、n=4或n=6时,λn结果如下:
(6)
相邻两个圆的重叠面积占整个圆面积的百分比越小,所需要的小圆个数越少,式(6)表明正六边形能够通过使用最少结点覆盖整个大圆范围的面积。因此,当短电弧小圆半径为r时,以它的内接正六边形对大圆区域进行覆盖,可实现重叠覆盖率最小的完全覆盖,即正六边节点覆盖模型。每一个短电弧的覆盖率ηs为短电弧小圆内接正六边形面积As与短电弧小圆Al之比,即:
(7)
使用正六边形密排方式代替小圆对大圆区域进行完全覆盖,即要求大圆边界要在最外侧正六边形最远端顶点内。正六边形的密排方式有以下3种方式:
(1)正六边形中心位于大圆圆心处,其他正六边形依次向外扩展;
(2)3个正六边形顶点位于大圆圆心处,其他正六边形依次向外扩展;
(3)正六边形顶点位于大圆内任意位置且不与大圆圆心重合,其他正六边形依次向外扩展。
由于圆和正六边形都是中心对称图形,当大圆圆心在任意位置时,必有一象限需要额外六边形覆盖,因此方式3用来完全覆盖大圆的正六边形个数无法达到最小值,因此本节着重讨论方式1与方式2的六边形覆盖情况。方式1和方式2的简要示意图如图2所示。

图2 两种方式示意图
1.3 模型求解

使用AutoCAD软件绘图验证示意如图3所示,对半径为1 000 mm的大圆用外接圆为60.5 mm的正六边形进行填充,此时正六边形中心与大圆圆心重合,实现对大圆的完全覆盖。对图4中的六边形的个数进行计数,得367个,可以证明经过MATLAB计算所获得的程序能够得到与实际值相同的结果,程序可靠。
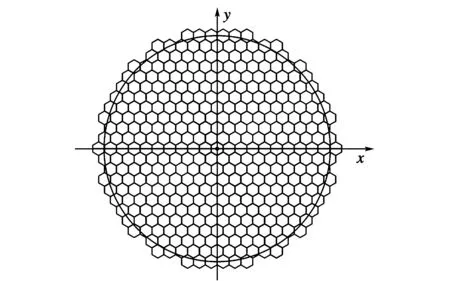
图3 正六边形中心与大圆圆心重合
当正六边形的顶点位于大圆圆心处时,经MATLAB计算得出最少需要378次半径为60.5 mm的短电弧加工才能够对半径为1 000 mm的圆形材料实现完全覆盖。
使用AutoCAD软件绘图验证如图4所示,对半径为1 000 mm的大圆用外接圆为60.5 mm的正六边形进行填充,此时3个正六边形顶点与大圆圆心重合,实现对大圆的完全覆盖。对图4中的六边形的个数按行进行计数,得到共需378个短电弧才能够实现完全覆盖。
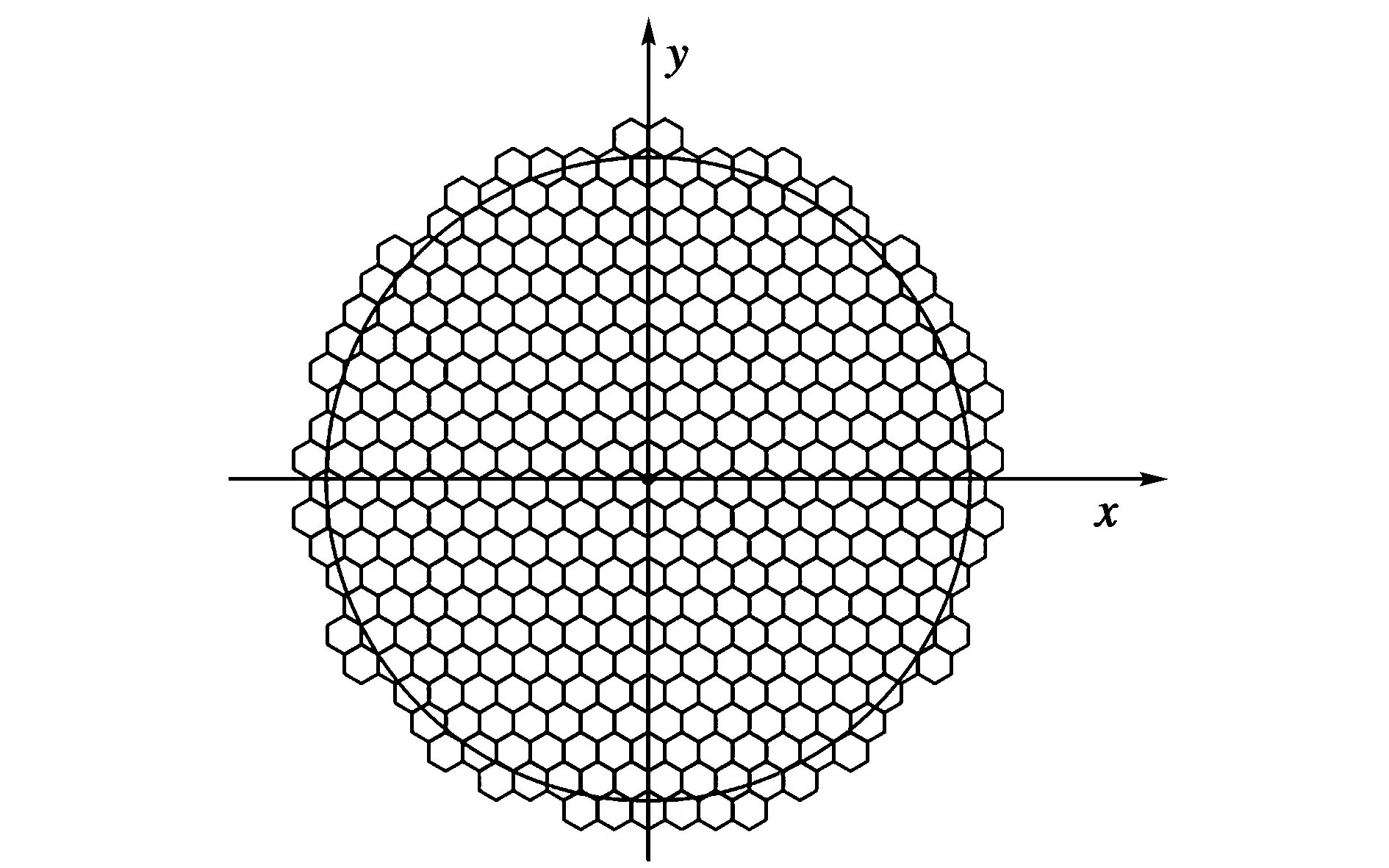
图4 三个正六边形顶点与大圆圆心重合
1.4 模型对比
两种模型结果见表1。
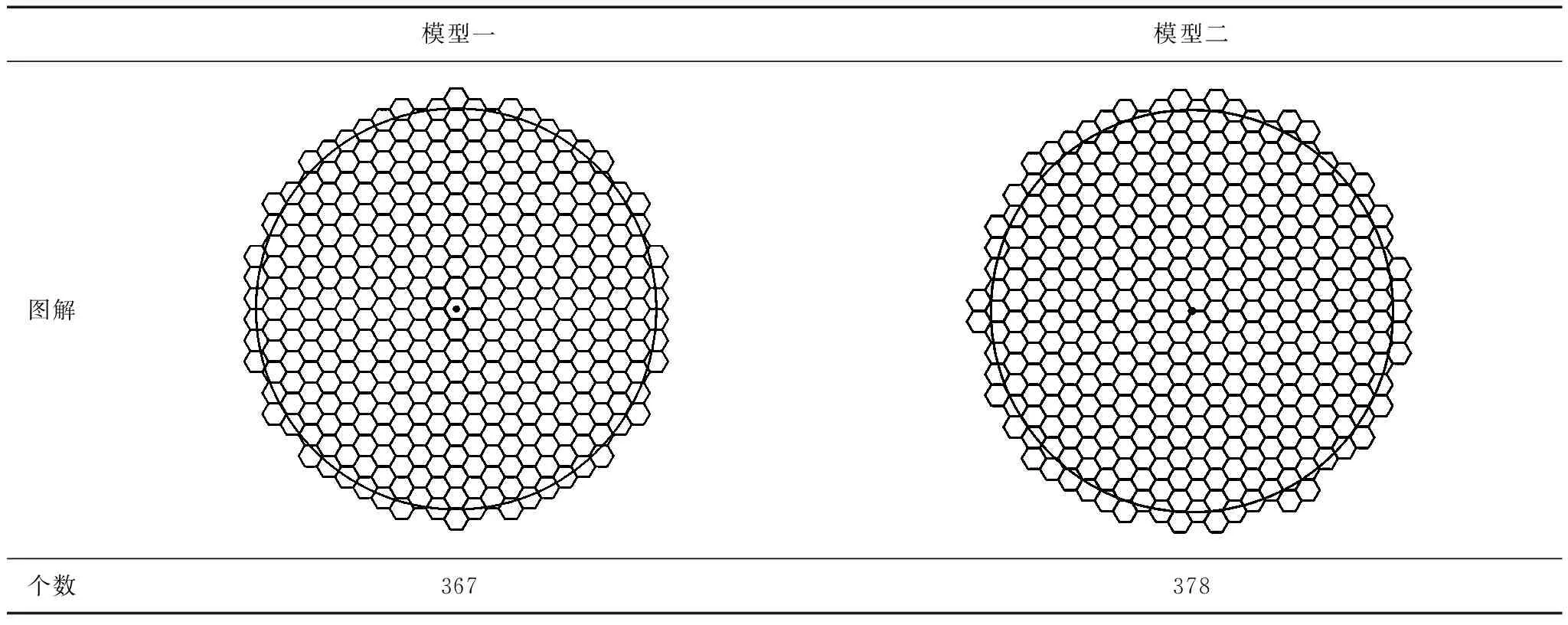
表1 两种模型结果
由表1可以看出,相比模型二,模型一不仅正六边形使用个数更少,且对正六边形的利用率更高。因此,当使用半径为60.5 mm的短电弧加工方式加工半径为1 000 mm的圆形材料时,模型一能够使加工次数达到最少,最少的加工次数为367次。
2 问题拓展
同理,当短电弧半径改为65.5 mm、70.5 mm和75.5 mm,圆形材料半径不变时,依然可以使用正六边形模型。
2.1 短电弧半径为65.5 mm
短电弧半径为65.5 mm时,首先使用MATLAB进行求解,圆心位置不同时,得到最小加工次数分别为313个和321个;使用AutoCAD绘图软件绘图验证,大圆圆心位于正六边形中心和大圆圆心位于正六边形顶点时,求解结果对比见表2。

表2 短电弧半径为65.5 mm时的结果
由上表可以得出,短电弧半径为65.5 mm的时候,至少需要313次短电弧加工才可以对半径为1 000 mm的圆形材料实现表面完全覆盖加工,此时大圆圆心位置在正六边形中心位置,即采用模型一方式比模型二方式更好。
2.2 短电弧半径为70.5 mm
短电弧半径为70.5 mm时,首先使用MATLAB进行求解,得到最小次数分别为283个和282个,使用AutoCAD绘图软件进行绘图验证,大圆圆心位于正六边形中心和大圆圆心位于正六边形顶点时,求解结果对比见表3。

表3 短电弧半径为70.5 mm时的结果
由上表可以得出,短电弧半径为70.5 mm的时候,至少需要282次短电弧加工才可以对半径为1 000 mm的圆形材料实现表面完全覆盖加工,此时大圆圆心位置在正六边形顶点位置,即采用模型二方式比模型一方式更好。
2.3 短电弧半径为75.5 mm
短电弧半径为75.5 mm时,首先使用MATLAB进行求解,得到最小次数分别为253个和246个,使用AutoCAD绘图软件进行绘图验证,大圆圆心位于正六边形中心和大圆圆心位于正六边形顶点时,求解结果对比见表4。
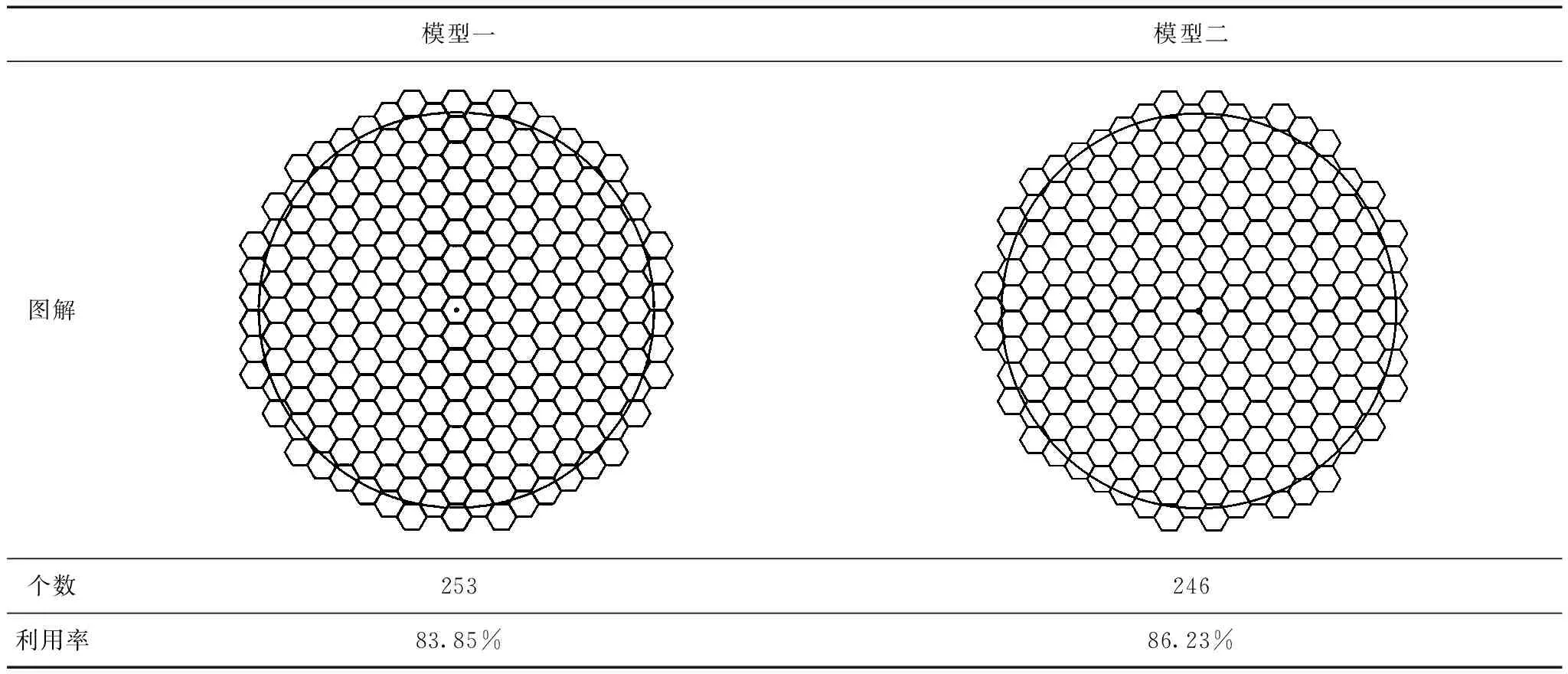
表4 短电弧半径为75.5 mm时的结果
由上表可以得出,短电弧半径为75.5 mm的时候,至少需要246次短电弧加工才可以对半径为1 000 mm的圆形材料实现表面完全覆盖加工,此时大圆圆心位置在正六边形顶点位置。
总结,当短电弧半径分别为60.5 mm、65.5 mm、70.5 mm和75.5 mm时,短电弧最少覆盖次数见表5。

表5 短电弧最少覆盖次数
如何更好的获得短电弧最少覆盖次数,然后可以根据此方法优化改进短电弧加工方式,减少加工成本,一直是短电弧加工制造探索的重点。近年来,神经网络因其优秀的数据拟合与预测性能,已在许多领域得到了较好的应用,如果能将这种技术应用于短电弧最少覆盖次数的研究,将会大大减少短电弧加工成本的支出。
3 神经网络预测模型
3.1 神经网络理论
BP(BackPropagation)神经网络是一种在生物神经网络的启发下建立的数据处理模型,并依据逆向算法训练的多层前馈型神经网络。BP网络结构如图5所示,其结构通常由输入层、隐含层和输出层组成。信息正向传播,而误差反向传播。在正向传播过程中,向输入层中输入n组数据样本作为输入信号,经隐含层计算后传递至输出层,输入层与隐含层及隐含层与输出层之间均采用权重进行连接。当在输出层未能得到预期的训练结果时,计算输出层的误差变化值,并将误差反向传播。之后,根据误差修改各层之间的权重,直至输出信号达到期望目标,停止训练并输出结果。其优点可以概括为自学习和自适应性强、容错率高、具有较高的计算精度和储存速度[3],所以本文将使用BP神经网络作为预测模型。
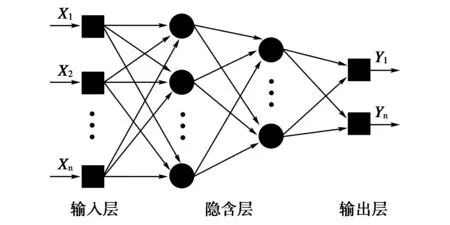
图5 BP网络结构
3.2 生成训练数据
当圆形材料R与短电弧小圆半径r变化时,最少短电弧覆盖次数就是一个二元方程,其最少次数与圆形材料R与短电弧小圆半径r都有关系,即:
n=f(r,R)
(8)
且圆形材料R与短电弧小圆半径r是基本参数,两者没有相关性。
利用MATLAB生成当圆形材料半径R=1 000 mm时,短电弧的半径r从40.5~239.5 mm,计算出最少短电弧覆盖次数,共200个数据,然后当圆形材料半径R=1 001 mm时,短电弧的半径r从40.5~239.5 mm生成200个数据,计算出最少短电弧覆盖次数,以此类推,直到圆形材料半径R=1 199 mm时,总共生成40 000(200*200)组输入为大圆半径R与小圆半径r,输出为短电弧最少覆盖次数的数据。部分数据见表6。

表6 部分训练数据
3.3 模型的建立与预测
模型建立前,需要确定输入层、输出层、隐含层节点数等参数[6]。
对于输入层,需要各个变量之间没有相关性或较低相关性,圆形材料R与短电弧小圆半径r是基本参数,两者没有相关性,同时直接影响最少覆盖次数[5]。
BP神经网络的一个隐含层就可以以任意精度逼近任意的非线性函数,其隐含层节点数目可以根据式(9)确定,经多次实验,最终确定隐含层节点数为5。
(9)
式中:m为隐含层节点数目;n为输入层神经元数目;l为输出层神经元数目;α为1~10之间的常数。
将数据导入Neural Fitting Tool工具箱,输入为大圆半径R与小圆半径r,输出为短电弧最少覆盖次数,并进行随机排列,将排列后的数据集按70∶15∶15的比例分给训练集、验证集与测试集。
随后将这些数据集代入一个具有1层5节点数的网络,进行训练,其网络模型结构如图6所示,模型中各结构参数见表7,训练过程如图7所示,各组训练结果如图8所示。

图6 网络模型结构

表7 模型结构参数取值

图7 训练过程
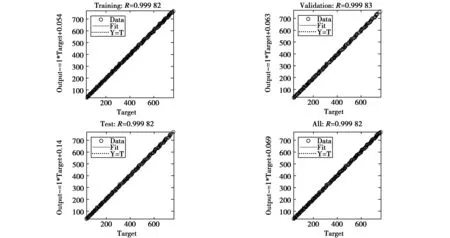
图8 各组训练结果
最后可以得到训练组、验证组与测试组的相关系数分别为0.999 82、0.999 83、0.999 82,从而可以得出BP网络对于短电弧最少覆盖次数具有精确预测能力。
4 结论
验证并选用正六边形模型对短电弧最少覆盖次数进行求解,利用MATLAB计算出不同短电弧半径下最少覆盖次数,并生成40 000组训练数据,利用BP神经网络,对数据集进行训练与预测,结果预测较好,因此可以使用BP神经网络对短电弧最少覆盖次数进行预测。
