基于刀具轮廓控制的曲面零件抛光自适应补偿研究

万志鹏，刘高飞，陈满意，朱自文

(武汉理工大学 机电工程学院，湖北 武汉 430070)

在工业机器人抛光技术领域，为提高工件的表面抛光质量，一般采用恒力控制进行抛光[1-2]，但对于部分刀具而言，刀具的磨损对抛光力有着较大的影响，因此，如何分析刀具磨损后的轮廓模型、如何调整刀具补偿量、如何实时调整期望抛光力的大小，仍是需要解决的一个难题。

在刀具磨损研究方法中，一方面是通过分析刀具与曲面的接触情况，建立刀具的曲面磨抛模型，优化工艺参数，从而使得刀具的磨损均匀，改善刀具的磨损状况[3]；另一方面是通过建立Preston假设或其他材料去除模型来分析刀具材料的去除率，从而探讨刀具材料的去除情况[4-5]。以上研究刀具磨损的方法没有考虑刀具磨损后的轮廓变化较大而影响刀具材料去除模型的精度。对于复杂凹形曲面来说，刀具磨损是一个动态变化的过程，考虑到工件抛光过程中接触点法向量的变化，还需建立完整的刀具轮廓数据，以减小刀具轮廓误差，从而提高加工精度。刀具轮廓检测包括轮廓在线检测和轮廓在线预测，程颖等[6]通过建立一套光学系统来获取刀具加工面的图像，经图像处理获取刀具的轮廓位置信息，但考虑到图像识别受外界环境的影响较大，很难适用于抛光等粉尘较多的场合。余杭卓等[7]通过正交试验获取了刀具的回转轮廓误差数据库，根据其数据，建立了刀具回转轮廓误差的预测模型，但该预测模型并不适用于球形抛光刀具的轮廓预测。

在自适应力控制方面，Wang等[8]在机器人去毛刺过程中，根据机器人第六关节末端位置和期望位置的误差，采用模糊阻抗控制器来调整阻抗参数，提高控制器的稳定性，从而提高加工精度，通过实验验证了柔顺控制策略的有效性。Zhang等[9]分析接触力/扭矩的感知，建立了重力补偿变换矩阵，通过矩阵重组进行参数辨识，并设计了基于模糊PID(proportional integral derivative)的混合力/位置混合控制控制，从而实现主动力控制。Himanshu等[10]提出了一种基于ANFIS-PD+I(adaptive neurofuzzy inference system-proportional derivative+integral)的混合力/位置控制器，该控制器可以有效地处理存在外部干扰的未知机器人动力学问题，使得机器人更平滑地跟随期望路径。对于自由曲面而言，刀轨数据复杂，上述方法难以实现力位高精度的控制，因此，在考虑刀具磨损的情况下，提出一种基于刀具轮廓控制的曲面零件抛光自适应补偿方法，可提高曲面零件抛光的控制精度，提高抛光系统的柔顺性。

1 抛光工艺参数研究

在机械抛光过程中，工艺参数直接影响工件的抛光质量。采用砂轮、橡胶和羊毛毡等刀具对工件进行抛光时，刀具使用一段时间后会产生较大的磨损，而刀具磨损后的轮廓直接影响刀具和工件的接触条件，因此为改善工件抛光质量，需合理控制抛光力的大小以及刀具补偿量。为提高刀具补偿量的计算精度，必须考虑系统刚度所产生的影响。

1.1 刀具轮廓模型

机械抛光属于高转速低进给加工，刀具在加工时，只有部分轮廓参与了抛光，考虑到部分工件的加工刀轨数据复杂，并且刀触点的法向量一直在变化，采用圆弧代替接触轮廓则会存在较大的误差。因此将刀具轮廓离散化，其刀具轮廓数据计算模型如图1所示。根据法向角θp的不同来表示刀具的轮廓数据Rp，则刀具轮廓Lp的表示方法为：

Lp={Rp|θp→Rp},θp=0°,2°,…,180°

(1)

式中：θp为刀触点法向量与刀轴的夹角，即法向角；Rp为法向角所对应的轮廓数据。

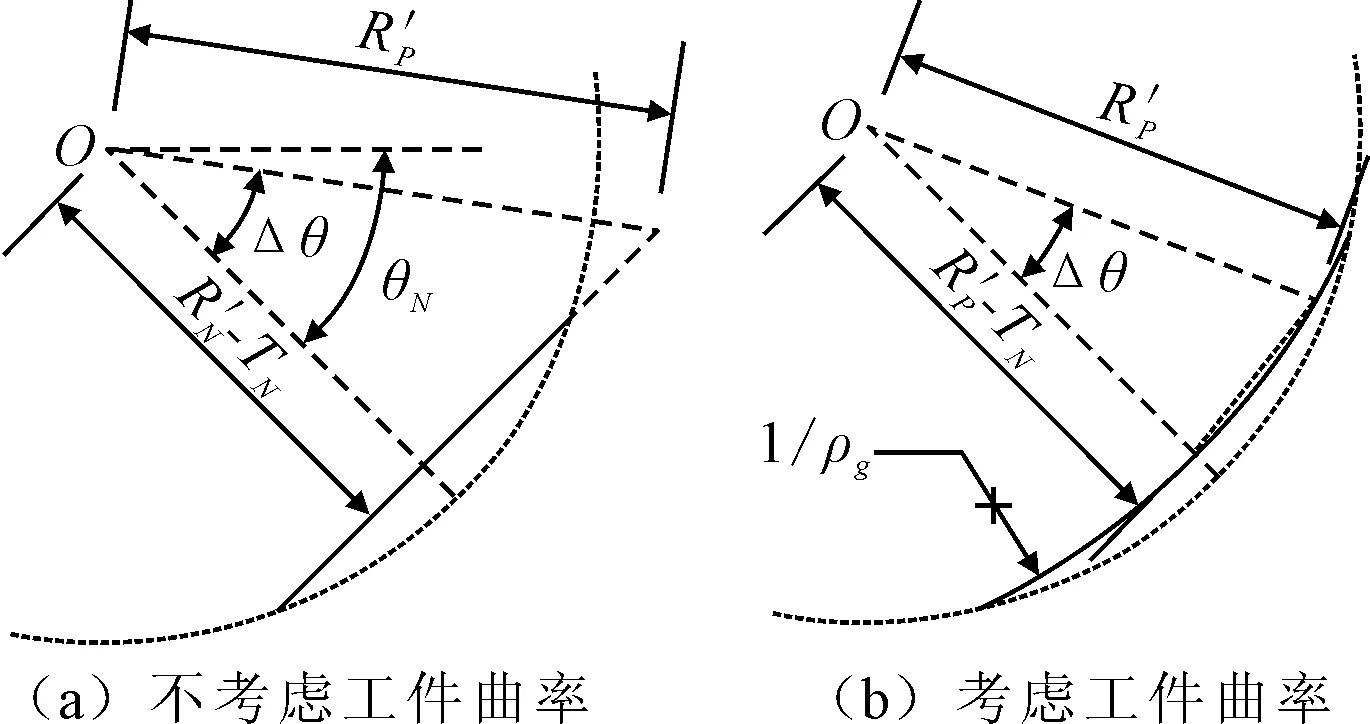
图1 刀具轮廓数据计算模型

刀具轮廓模型与工件加工点的曲率ρg有关，参与抛光的刀具轮廓外形的曲率会趋于加工点的曲率，因此，根据该位置下法向角所对应的磨损量，可以计算出其他参与抛光的刀具轮廓数据。当工件抛光点的曲率很小时，则该加工点所在的曲面趋于平面，可以将该处看作是球形刀具与平面接触。为区分出临界曲率，如果曲面某加工点的曲率半径与球形刀具半径R之比大于20倍，在计算时可忽略工件曲率，如图1(a)所示，则有：

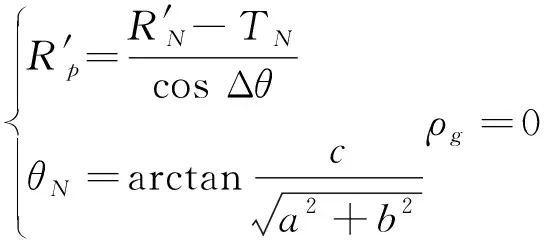
(2)

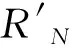
当θN确定后，θp的取值并不是从0至180°，而是在θN值的一定范围内选取，即Δθ的绝对值应小于一个随着刀具轮廓模型动态变化的角度，以提高刀具轮廓模型的计算效率。

如果曲面某加工点的曲率半径与球形刀具半径R之比小于20倍，在计算时则需考虑工件的曲率，如图1(b)所示，根据正弦定理，则有：

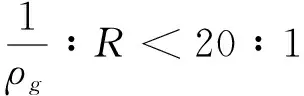
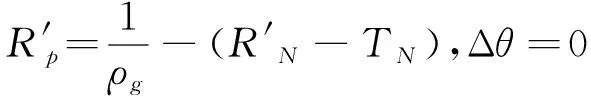
(3)

则当前通信周期内刀具轮廓所在的直线或圆弧曲线L′p表示方法为：

(4)

当前通信周期内刀具轮廓Lp(t)可表示为：

Lp(t)=min{Lp(t-1),L′p(t)}

(5)

1.2 系统刚度

打磨系统的结构由工业机器人、前端装置和刀具组成，为考虑刚度对刀具位置的影响，可将系统刚度分为本体结构刚度和刀具材料刚度，抛光系统所采用的工业机器人自身刚度较好，因此本体结构刚度可以看作是前端装置的刚度。对于不同刀具而言，抛光系统本体结构刚度一致，但刀具材料刚度会有一定的区别。假设抛光系统沿刀触点法向量的变形量为u，法向抛光力为Fn。为确定系统变形量与法向抛光力的关系，保证刀轴的方向竖直向下，在上位机上写好测试程序，控制机器人使得刀具缓慢的朝工件靠近，每个通信周期内刀具走0.05 mm，并获取法向抛光力的大小。为避免刀具在运动过程中发生碰撞，在法向抛光力大于30 N后，直接进行提刀操作。当刀具与工件接触时，法向抛光力会发生变化，以法向抛光力开始变大时作为标记，记此时的系统变形量为0，所采集的实验数据如图2所示。

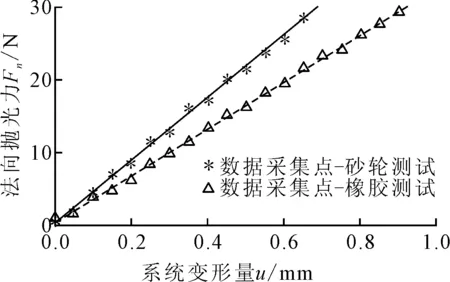
图2 系统变形量与法向抛光力之间的关系

抛光包含三道工序，分别为粗抛、半精抛和精抛，所采用的刀具分别为球形砂轮磨头、球形橡胶磨头和羊毛毡。砂轮磨头和橡胶磨头外形一致，磨损系数低，如果要保证工件的材料去除率均匀，则法向抛光力受刀具磨损的影响较大，必须合理控制法向抛光力才能获得较好的加工效果。与之不同的是，采用羊毛毡进行抛光主要是起到一个表面光整的作用，调整好期望力的大小即可保证较好的抛光效果。

假设等效刚度k为法向抛光力与系统变形量的比值，在图2中所采集的数据可以近似拟合成正比例函数，因此等效刚度可以看作是拟合直线的斜率，对砂轮磨头而言，砂轮材料的刚度很大，在外力的作用下所产生的变形量极为微小，因此砂轮拟合数据可以计算出系统本体结构的等效刚度。采用砂轮和橡胶磨头不影响系统本体结构的等效刚度，因此橡胶拟合数据所计算出的系统等效刚度为系统本体结构等效刚度和刀具材料等效刚度的综合。系统的本体结构等效刚度kb约为35 N/mm，橡胶材料的等效刚度kx约为88 N/mm。

根据刀具轮廓模型可以具体分析出法向抛光力的大小，便于调整抛光力自适应PI(proportional integral)控制的参数；由系统刚度引起的变形量和法向抛光力的关系可以精确地分析刀具刀位点所在的位置，便于调整抛光过程中的刀具沿法向量的刀具补偿量。

2 刀具位置自适应补偿研究

工业机器人抛光需要满足一定的位置精度要求，还需要获取较为精确的法向抛光力，并将其作为力反馈信号对机器人的加工轨迹进行刀具补偿。首先需根据刀具轮廓模型分析刀具的受力，再根据传感器所采集的三轴力计算出作用在刀具上力的大小，最后再通过力位混合控制调整刀具的补偿量，从而调整抛光力的大小。

2.1 抛光力分析与重力补偿

本系统采用ME3DT120三轴力传感器来采集刀具和工件接触的抛光合力，考虑到刀轴的方向会大幅度改变传感器所采集的数据，因此在前端装置和工件不产生干涉的情况下，尽可能保证刀具的刀轴方向垂直于水平面向下。刀具对工件的作用力即抛光合力Fd可分解为：法向抛光力Fn、周向抛光力Ff和切向抛光力Ft，如图3所示。当刀具以速度v沿着刀轨朝某个方向做进给运动时，刀具上下偏移量很小，因此切向抛光力Ft可以忽略不计。则抛光合力为：

Fd=Fn+Ff

(6)

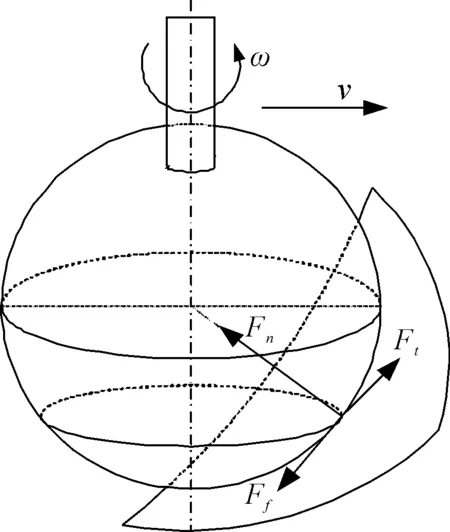
图3 刀具与工件接触力分析

传感器通过法兰板和主轴与刀具连接，传感器为三轴力传感器，则3个方向上的分力可用Fx、Fy和Fz表示，传感器测得的合力Fc主要由抛光合力Fd、传感器以下部分的重力FG和惯性力FI组成，因为刀具的进给速度v较小，所以惯性力FI与其他力相比会很小，可忽略不计，则有：

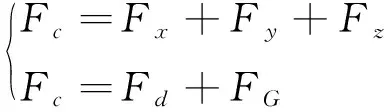
(7)

为进一步分析抛光力的大小，将每个力沿传感器的x、y、z方向进行分解并计算，化简得：

(8)

2.2 期望力分析

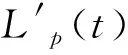
(9)

期望力与接触分段数成正比，当接触分段数较小时，理论情况下期望力较小抛光质量也较好，但是期望力变小后，其他所有接触力和传感器所测得的力都很小，所计算出来的法向抛光力的误差则会非常大，严重影响抛光的质量，因此，当接触分段数较小时，依然要使期望力不低于某个值，则期望力Fq和接触分段数LD的关系可为：

(10)

式中：Fqmin为最小期望力；KF为期望力与接触分段数的比例系数。

当接触分段数越来越大时，表示刀具磨损也变得更加剧烈，当分段数大于一定值时，就应该考虑更换刀具，采用新刀具来进行加工。

2.3 刀具自适应补偿与刀位点分析

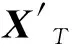
X′T=XT+Xf

(11)

在抛光过程中，法向抛光力Fn始终在期望力Fq的一定范围内波动，因此为保证法向抛光力的稳定，需要在法向量上进行一定位置补偿，才能使法向抛光力接近期望抛光力。在法向抛光力发生变化的同时，由系统刚度引起的变形量也在发生改变，因此计算补偿量的大小还需考虑系统变形量等因素，则有：

(12)

当法向抛光力Fn大于期望力Fq时，Xf为正，则刀具沿着法向量的正向进行补偿，从而将法向抛光力减小至期望值；当法向抛光力Fn小于期望力Fq时，Xf为负，则刀具沿着法向量的反向进行补偿，从而将法向抛光力增大至期望值。

如果前端装置刚度足够大，则刀位点和机器人第六关节末端中心点始终在同一条铅垂线上，但前端装置的刚度较差，因此刀位点和机器人第六关节末端中心点在有抛光力的作用下不会在同一条铅垂线上。假设抛光过程中刀位点的坐标为Xc，刀位点到机器人第六关节末端中心点的距离为H，则有：

(13)

刀轨数据中刀位点的坐标为Xd，根据刀具磨损后的状况，则有：

Xd=Xc+(R-RN)·(a,b,c)

(14)

根据式(11)～式(14)，可计算出刀具的磨损量RN，进一步计算出轮廓数据Rp。

2.4 机器人抛光自适应控制系统

期望抛光力的计算过程如图4所示。首先根据刀轨数据和机器人反馈数据等其他坐标量来计算刀具此时的磨损量，进而根据式(5)计算刀具的轮廓数据，最后根据刀具轮廓数据和式(10)计算期望抛光力Fq。

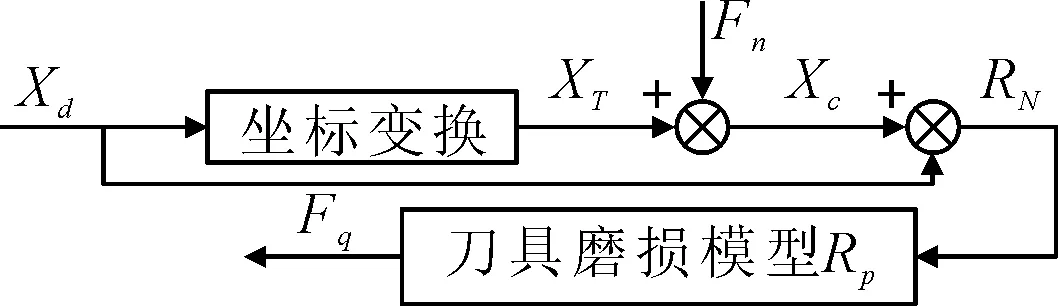
图4 期望抛光力计算过程

在基于位置控制的力位混合控制策略中，如果按照刀具补偿量调整刀位点的位置至期望位置，考虑到机器人运行过程中有着轻微的惯性冲击，下一时刻法向抛光力难以与期望抛光力一致，法向抛光力在短时间内很难达到平衡状态，因此，在对机器刀具进行位置补偿时，还需通过PI控制修正补偿量，使机器人抛光过程中法向抛光力更加平稳。力位混合控制过程如图5所示。

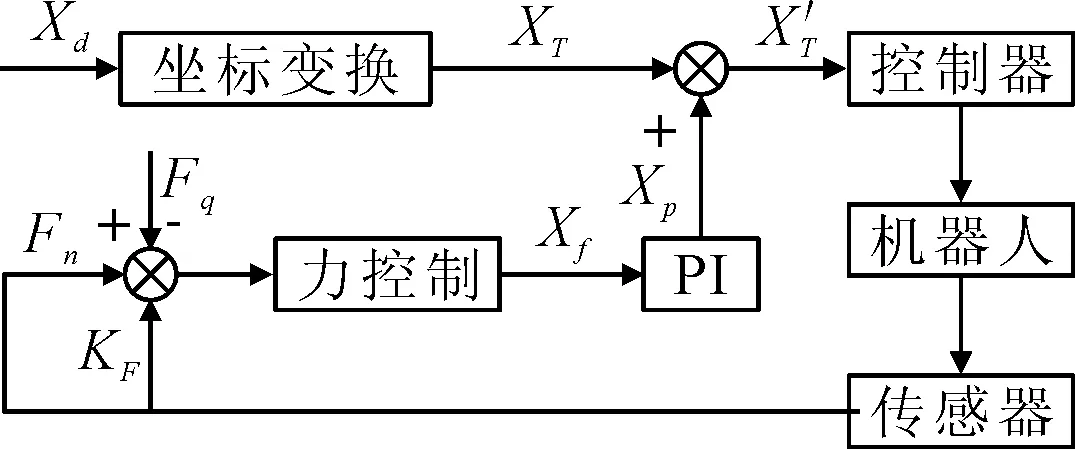
图5 力位混合控制过程

3 抛光系统搭建以及实验

3.1 抛光实验平台

为验证上述方法的可行性，搭建机器人自动抛光系统，如图6所示，前端装置包括传感器、主轴和连接板，其动力装置包括KUKA机器人和主轴，控制设备包括上位机、示教器和机器人控制柜，信号传输及采集设备包括ME3DT120三轴力传感器、信号放大器和PCIe-6320数据采集卡，抛光刀具包括球形砂轮磨头、球形橡胶磨头和羊毛毡，抛光对象为汽车轮毂模具。

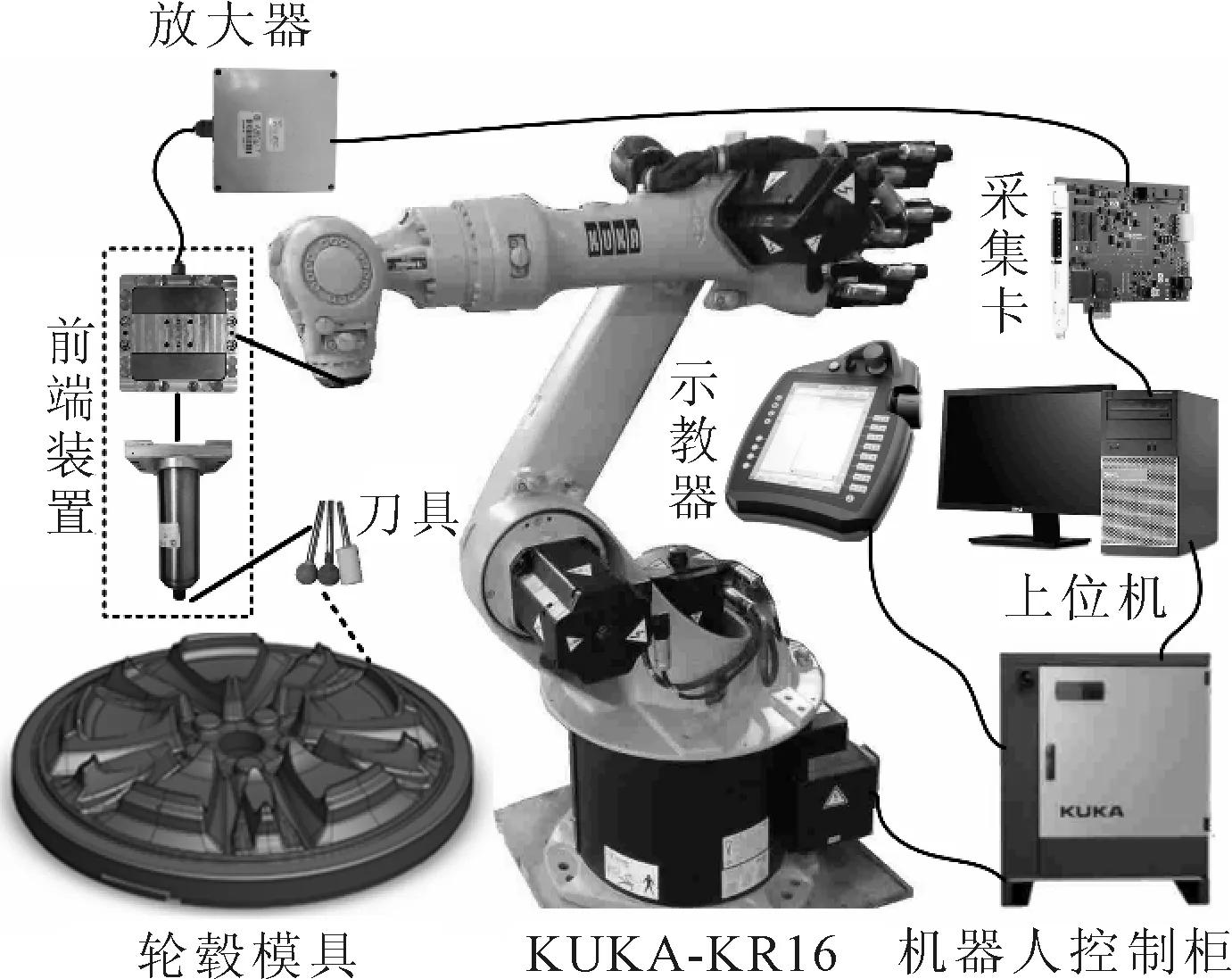
图6 机器人自动抛光系统

在抛光过程中会产生一定的抛光力，通过力传感器的测量数据可以分析并计算抛光力的大小；传感器所测得的电压信号通过放大器将信号放大，以减小电压信号的测量误差；在上位机上安装PCIe-6320数据采集卡，则在上位机的LabVIEW程序上可以获取该电压信号，并在LabVIEW中进行滤波及三轴力信号提取；在上位机抛光控制程序中，写入监听LabVIEW功能，以获取三轴力的大小；上位机抛光控制程序读入事先规划好的刀轨数据文件，根据三轴力的大小、刀具的轮廓数据和系统等效刚度，计算出法向抛光力、期望力和刀具补偿量等参数，并作为力位混合控制的输入参数；调整上位机抛光控制程序发送的刀位点增量数据，通过机器人控制柜，驱动机器人各关节从而带动刀具按照预期的轨迹运动，以达到良好的柔顺控制效果，并获取较好的抛光质量。

3.2 实验结果及分析

为提高轮毂模具的抛光质量，第一道工序采用球形砂轮磨头粗抛，第二道工序采用球形橡胶磨头半精抛，第三道工序采用羊毛毡精抛，配合7 μm金刚石研磨膏使用，第四道工序采用羊毛毡精抛，配合2.5 μm金刚石研磨膏使用，具体工艺参数如表1所示，其中n为主轴的转速，v为刀具的进给速度，因为机器人的运动方式为点到点的运动，所以速度用一个通信周期T内走过的长度来表示，W为金刚石研磨膏的粒度。

表1 不同抛光工序对应的工艺参数表

图7为汽车轮毂模具抛光前与抛光后的实验对比图，从图7可知，经过4道抛光工序加工后的轮毂模具，表面光洁度较好，粗糙度较低。为进一步测量不同工序的抛光质量，采用手持式粗糙度测量仪测量其轮廓算术平均偏差Ra，测量结果如表2所示。根据表面粗糙度的测量结果可知，工件表面粗抛完成后，可以看见明显的加工痕迹；工件半精抛完成后，工件的加工痕迹很小；工件在第一次精抛完成后，表面已经达到了暗光泽效果；工件在第二次精抛完成后，表面为亮光泽表面，将铅笔放置于其表面，可以看到较为清晰的倒影，也就是图7(b)所示的效果。

图7 轮毂模具抛光实验结果对比图

表2 粗糙度测量结果

图8为采用原导纳控制策略对平直曲面进行抛光的抛光效果，与图7(b)采用自适应抛光控制策略对自由曲面进行抛光的抛光效果对比，可以发现， 在图7(b)中，铅笔的倒影更加明显，倒影纹路更清晰，抛光质量更好，粗糙度对比结果如表3所示。

图8 原导纳控制策略抛光效果

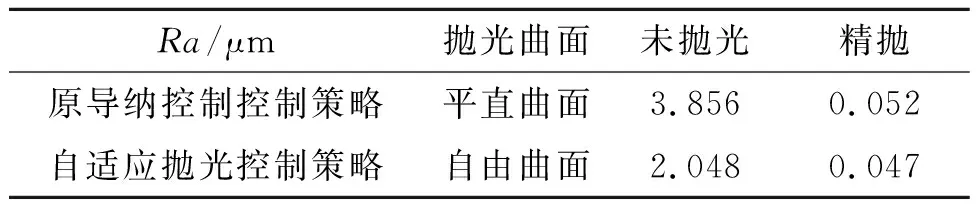
表3 自适应控制方法与原控制方法对比

4 结论

从机器人抛光工艺的角度出发，首先分析了刀具磨损和系统刚度给轮毂模具抛光所带来的影响，建立了刀具轮廓模型。根据该模型分析期望抛光力的大小，从而动态调整抛光的工艺参数。然后根据刀具轮廓模型和系统刚度分析结果，进一步分析刀具的受力以及位置控制，提出了一种基于位置控制的力位混合控制方法，从而提高机器人抛光的自适应性。实验表明，采用该控制方法对自由曲面进行抛光，其抛光质量更好。