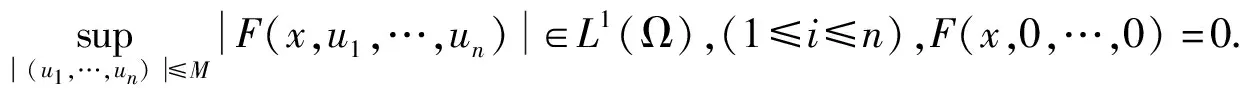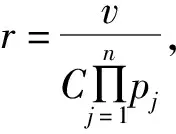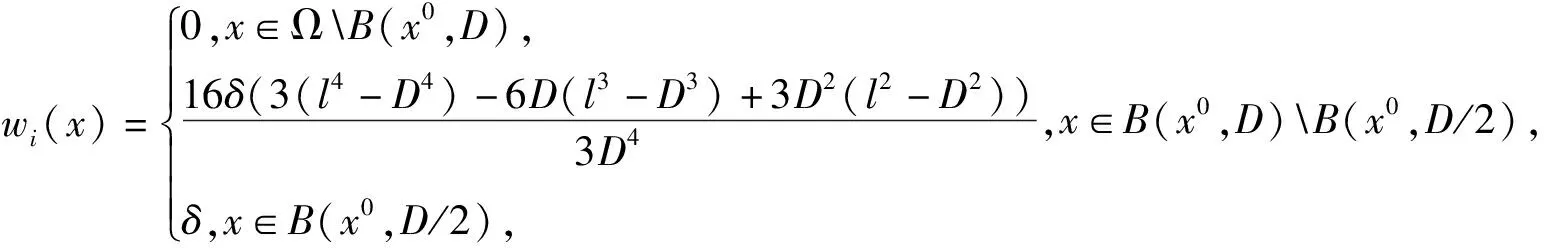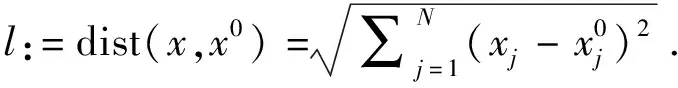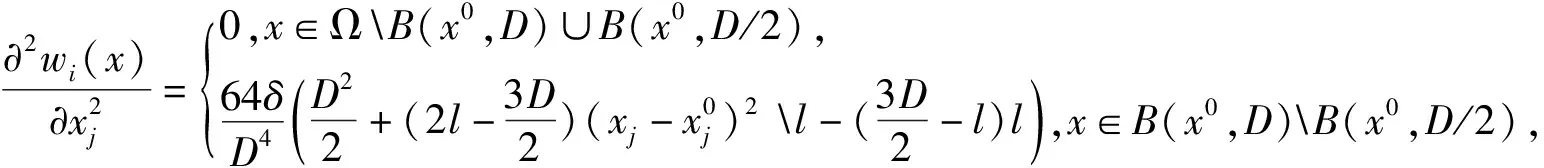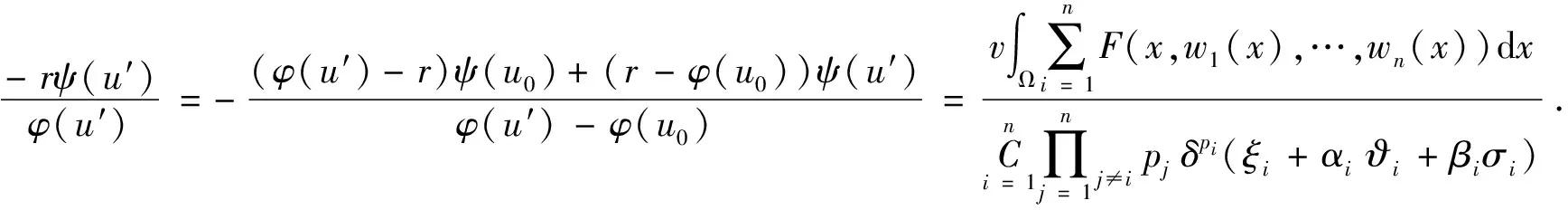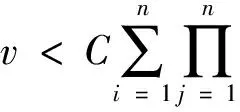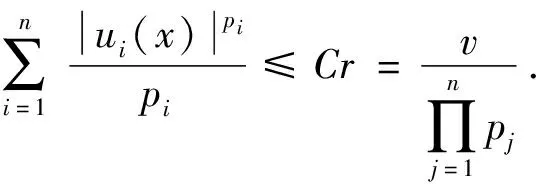带Navier边值条件的(p1,…,pn)双调和方程组多解性研究
2022-03-26吴丹阳
吴丹阳,缪 清
(云南民族大学 数学与计算机科学学院,云南 昆明 650500)
弱解的存在性,得到了问题至少存在3个弱解的充分条件.
主要研究了带有Navier边值条件(p1,…,pn)的双调和系统
(1)
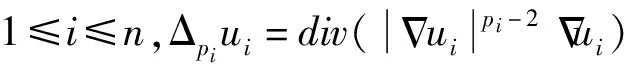
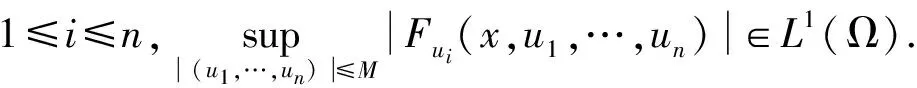
(F2)对任意的x∈Ω,F(x,0,…,0)=0.
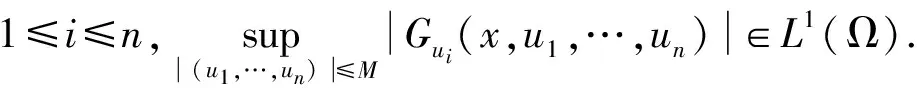
非线性四阶椭圆型边值问题近年来得到了很多研究.文献[1]中指出,此类型的非线性方程来源于悬索桥行波的模型研究,同样梁的静态形式变化或刚体的运动也可以用非线性四阶方程来描述[2-5,7-10].在文献[11]中,作者考虑了下述带有Navier边值条件的p-双调和方程
(2)
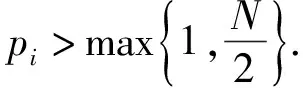
f:Ω×R→R是连续函数,g:Ω×R→R是Caratheodor函数, 利用Ricceri[6]的临界点理论得到:存在一个开区间Λ⊆[0,+∞)和一个正实数ρ,使得对任意的λ∈Λ,方程(2)至少存在3个弱解.文献[12]中,作者讨论了含有Navier边值条件的(p,q)双调和问题的多解性.在文献[13]中,由Ricceri三临界点理论,作者证明了对于下述带有Navier边值条件的(p1,…,pn)双调和问题至少存在3个弱解:
(3)
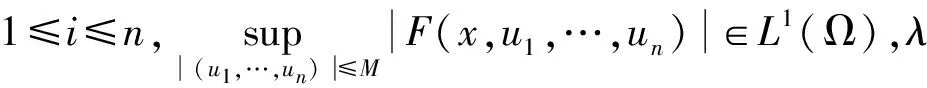
1 预备知识
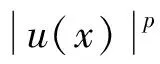
定义1.2[14]设Ω⊂Rn是一个开集,k是非负整数,1≤p≤∞,称集合Wk,p(Ω)={u∈Lp(Ω)|∂αu∈Lp(Ω),|α|≤k}.按照范数
(4)
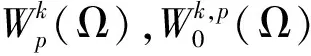
记
(5)
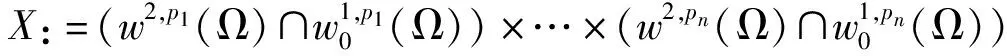

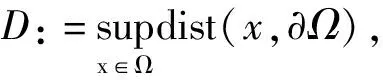
其中1≤i≤n,这里Γ表示Gamma函数.对任意的γ>0,令集合
2 主要结论
定理2.1[15]X是可分的自反的实Banach空间,φ:X→R是一个连续Gateaux可微且序列弱下半连续的函数,它的Gateaux导数在X*上连续,ψ:X→R是连续Gateaux可微函数,它的导数是紧算子.假设
(2)φ(u0) 则存在一个非空开集Λ⊆[0,+∞)和一个正实数σ有以下性质:对每一个λ∈Λ和每个连续函数J:X→R,它的Gateaux导数是紧算子,存在δ>0使得对每个μ∈[0,δ].方程φ′(u)+λψ′(u)+μJ′(u)=0在X中至少有3个解,并且它们的范数小于σ. 定义2.1如果u=(u1,…,un)∈X是方程组(1)的弱解,那么对任意(v1,…,vn)∈X满足 那么对一切x∈Ω和ui∈Rn,存在一个开区间Λ⊆[0,+∞)和一个正实数q,使得对每个λ∈Λ,问题(1)在X中至少存在3个弱解且它们的范数小于q. 证明:对任意的u=(u1,…,un)∈X,定义函数φ,ψ,J:X→R, 由于φ,ψ,J在X的每个有界子集上是有界的连续Gateaux可微的函数,且在点u=(u1,…,un)∈X处对一切(v1,…,vn)∈X满足: 因为φ′:X→X*是X中一致单调的算子[16,推论2.2],所以φ是序列弱下半连续函数.下面证明ψ′:X→X*是紧算子:根据文献[17],对任意u=(u1,…,un)∈X,当m→∞时,(u1,m,…,un,m)在X中弱收敛于(u1,…,un),即当m→∞时,(u1,m,…,un,m)在Ω上一致收敛于(u1,…,un).对每个x∈Ω,F(x,…)在Rn中是连续的,F的导数在Rn中也是连续的,所以当1≤i≤n时,Fui(x,u1,m,…,un,m)强收敛于Fui(x,u1,…,un),因此ψ′在X上是强连续的.由于X是自反空间,存在有界序列(u1,m,…,un,m)使得,当m→∞时,(u1,m,…,un,m)在X中弱收敛于(u1,…,un),所以当m→∞时ψ′(u1,m,…,un,m)强收敛于ψ′(u1,…,un),即证ψ′是紧算子. 因此,φ(u0)=ψ(u0)=0, 所以对一切x∈Ω和u=(u1,…,un)∈X,使得φ(u)≤r.又由于 至此,定理2.1的所有条件都满足,所以双调和方程组(1)至少存在3个弱解.