基于BP神经网络的合成纤维土价格预测模型研究
2022-03-26杨悦袁小永
杨悦,袁小永
(安徽国防科技职业学院 城市建设学院,安徽六安 237011)
0 引言
人工合成纤维加入土体中会形成三维加筋的复合效果,能够提高土体受力性能。合成纤维作为一种土工复合材料在工程中应用广泛。合成纤维土技术可以用于处治边坡、修改挡墙、处理软基、加固路堤,也可用于抗噪音保护和抗冲击保护等。若能够建立起合成纤维土的价格模型,将便于测算在无机稳定土中掺加无机结合料及纤维的成本价格,选择最经济的组合。本文依据袁小永、杨悦[1]测得的无侧限抗压强度值,结合不同纤维的特性,基于BP神经网络在MATLAB软件中建立价格模型,将模型预测值与实际值作对比,研究该模型的准确性。
1 BP神经网络的特点
人工神经网络作为一种信息处理技术,具有很强的模式识别和数据拟合能力。目前,人工神经网络的预测技术理论研究已较为成熟[2-3]。20世纪80年代中期,Rumelhart和McCelland等科学家提出了BP神经网络的概念。BP神经网络作为人工神经网络算法的一个分支,能够广泛应用于模式识别、函数逼近、分类、数据压缩等方面[4]。该种模型可以将不同的应用问题进行数学转化,通过数学优化分析训练样本的输入和输出[5]。
BP神经网络是一种多层次的神经网络。网络结构主要包括三类:输入层、隐含层和输出层[6]。每一层神经元无连接,层与层之间全连接。因此,输入层中的相关信息能够被更多地挖掘,BP神经网络能够完成更复杂的任务。由于BP神经网络采用误差反向传播算法进行学习,数据是从输入层、隐含层向后传播,训练网络权值沿着误差减少方向,从输出层逐层向前修正网络连接权值,因此,随着学习的进行,误差会越来越小。BP神经网络的传递函数是可微的,常用的传递函数是线性函数或Sigmoid函数。
BP神经网络模型计算过程见图1。通过输入训练样本、训练模型,预测样本仿真测试,计算出模型预测值和实际值,对比两者的相对误差,得出合理的预测模型。

图1 BP神经网络模型计算过程
2 数据处理
2.1 指标选取
试验模型主要用来预测合成纤维土的价格,根据袁小永、杨悦[1]纤维加筋无机稳定土的无侧限抗压强度试验,并查阅相关资料,最终确定指标为材料类型、纤维掺量、纤维长度、纤维种类、无侧限抗压强度、单方造价。
2.2 指标量化
在选取预测模型指标后,需要将其量化,具体量化方法为:
(1)材料类型
根据纤维土的无侧限抗压强度试验研究[1],本次材料类型主要有:掺入水泥的土体、掺入石灰的土体、掺入粉煤灰的土体,量化后分别为:水泥土为1、石灰土为2、粉煤灰土为3。
(2)纤维种类
试验模型所选的纤维主要有:聚乙烯醇纤维、聚丙烯纤维、聚酯纤维。量化后分别为:聚乙烯醇纤维为1、聚丙烯纤维为2、聚酯纤维为3。
(3)纤维掺量
纤维掺量按照实际掺量比例计入,试验模型的纤维掺量主要有0.1%、0.3%、0.5%三种。
(4)纤维长度
纤维长度按照实际长度计入,主要有6mm、9mm、12mm三种。
(5)无侧限抗压强度
无侧限抗压强度按照试验测得[1]。具体方法是将各种类型纤维土制成为高度100mm、直径50 mm的圆柱体试样,用保鲜膜将其包裹并放入密封袋中养护3天,测各样品的无侧限抗压强度值,单位为MPa。
(6)单方造价
单方造价为原材料单方土体的价格,采用2021年2期信息价。
以上各指标量化后数据处理结果见表1。
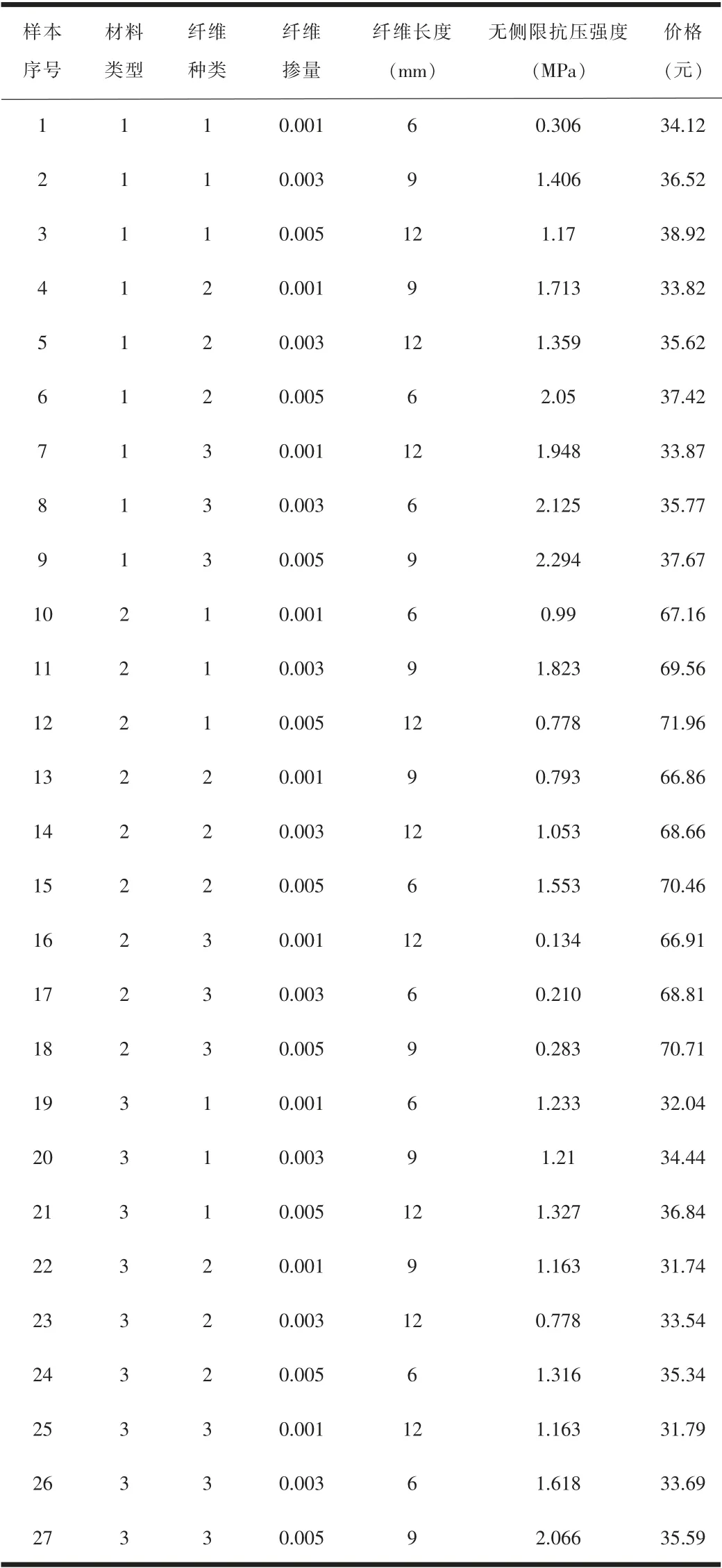
表1 指标定量化数据处理结果
3 模型构建
3.1 数据预处理
在MATLAB软件中,自编函数将表1中数据随机选取24组作为训练样本,剩余3组作为测试样本。这样的设置增加了数据选取的偶然性,比人为选择样本集和测试集更为接近实际情况。材料类型、纤维掺量、纤维种类、纤维长度、无侧限抗压强度指标作为输入变量P,单方造价作为输出目标T。训练样本中,输入变量用P_train表示,输出目标用T_train表示;测试样本中,输入变量用P_text表示,输出目标用T_text表示。由于输入特征具有差异性,为便于输入和训练,需要将数据进行归一化处理,本模型采用最大最小值归一化,输入为初始值、初始值最大值和最小值,输出为0到1的数值,具体计算公式如下:
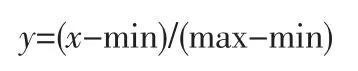
利用上式将训练样本输入输出值以及测试样本的输入值归一化后,分别用p_train、t_train、p_text表示。
3.2 创建网络
通过MATLAB软件中的newff函数创建BP网络。newff函数语法为:
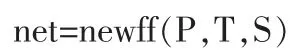
其中,P为神经网络输入变量,T为神经网络输出目标,S为隐含层神经元个数。目前没有确定合理的神经元个数的理想解析式,通常的做法是采用经验公式给出估计值,这里采用下式进行估算:
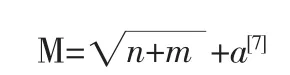
式中,m指的是输出层的神经元个数,n指的是输入层的神经元个数,a是[0,10]之间的常数[8]。本模型隐含层神经元个数取4,设置:net=(p_train,t_train,4)。
3.3 训练网络
设置训练参数:迭代次数1000次,训练目标10-3,学习率0.01。在MATLAB软件中用函数train训练,train函数语法为:
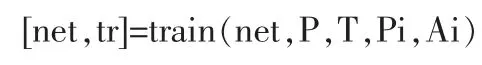
其中,Pi为初始输入延迟条件,Ai为初始层延迟条件。通常可以只设置net、P、T这三个参数。本模型设置训练网络:net=train(net,p_train,t_train)。
该模型的4次仿真结果回归拟合图见图2。
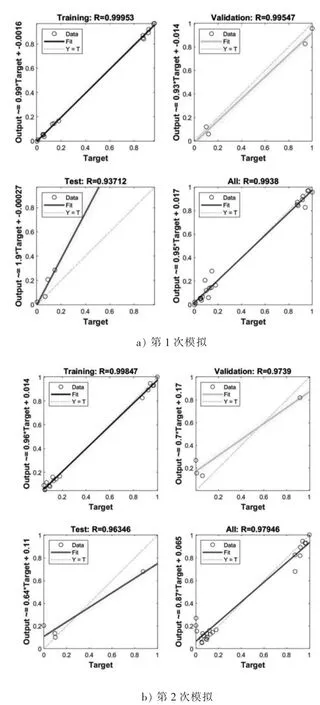
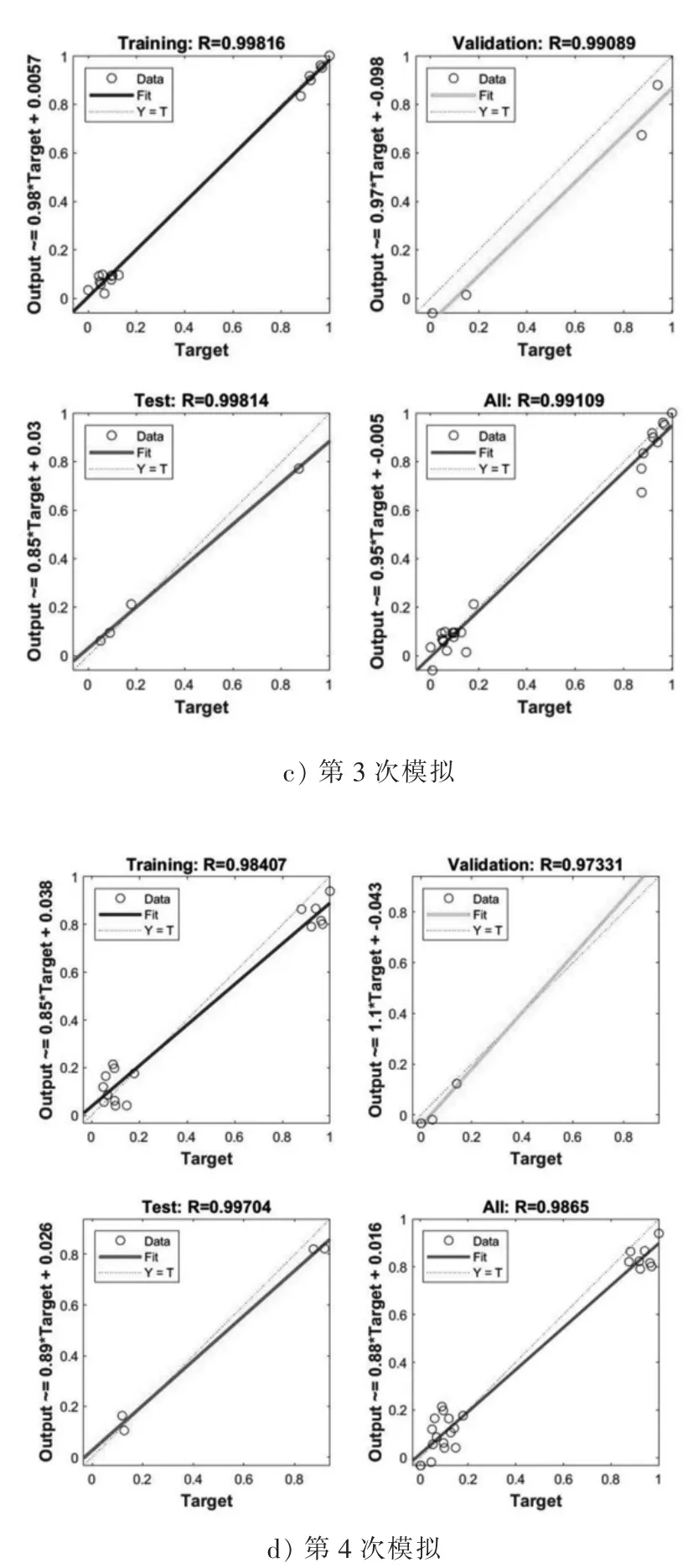
图2 仿真结果回归拟合图
从图2可以看出:第1次模拟的训练样本的拟合相关系数为99.95%,检测样本为99.95%,测试样本为93.71%,整体为99.38%;第2次模拟的训练样本的拟合相关系数为99.85%,检测样本为97.39%,测试样本为96.35%,整体为97.95%;第3次模拟的训练样本的拟合相关系数为99.82%,检测样本为99.09%,测试样本为99.81%,整体为99.11%;第4次模拟的训练样本的拟合相关系数为98.41%,检测样本为97.33%,测试样本为99.70%,整体为98.65%。每组相关系数均大于93%,说明该模型的训练效果较好,可以通过本次试验模型预测不同特性纤维土的价格。
3.4 仿真测试
本次试验模型的仿真测试是通过MATLAB软件中函数sim实现对测试数据进行计算分析,sim函数语法为:
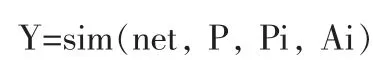
其中,Y为神经网络对输入变量P的实际输出,Pi和Ai可以不用输入,采用系统默认值。本模型仿真测试设置为t_sim=sim(net,p_test)。利用上述训练好的BP神经网络模型,对剩余3组数据进行检测分析。将输出的结果t_sim进行数据反归一化,结果为T_sim。
3.5 检测结果分析
将预测结果T_sim与输出目标T_text对比,即将纤维土的单方造价预测值与实际值作对比,在MATLAB软件中计算相对误差。由于该模型是在27组数据中随机选取24组作为样本集,3组作为测试集,所以每次运行模型产生的结果并不相同。为增加研究的科学性,试验模型在MATLAB软件共运行4次模型代码,每次运行均计算决定系数R2,用决定系数R2判断模型预测值与实际值的拟合效果。在MATLAB软件中绘制测试样本预测效果对比图,见图3。
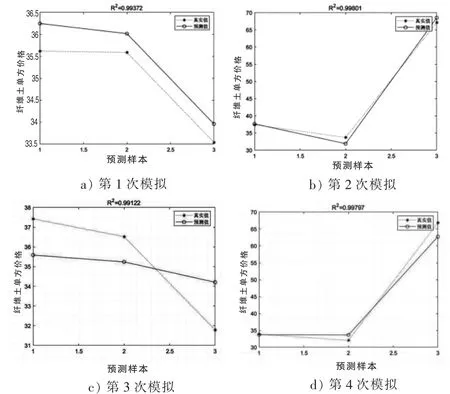
图3 测试样本预测效果对比图
由图3可以看出,第1次模拟R2为99.37%,第2次模拟R2为99.80%,第3次模拟R2为99.12%,第4次模拟R2为99.80%。由4次模拟结果来看,决定系数R2均大于99%,表明预测值与真实值拟合效果均较好,模型训练效果较好。
分别计算每次运行的测试样本的预测值与实际值相对误差,并求取平均值,见表2。
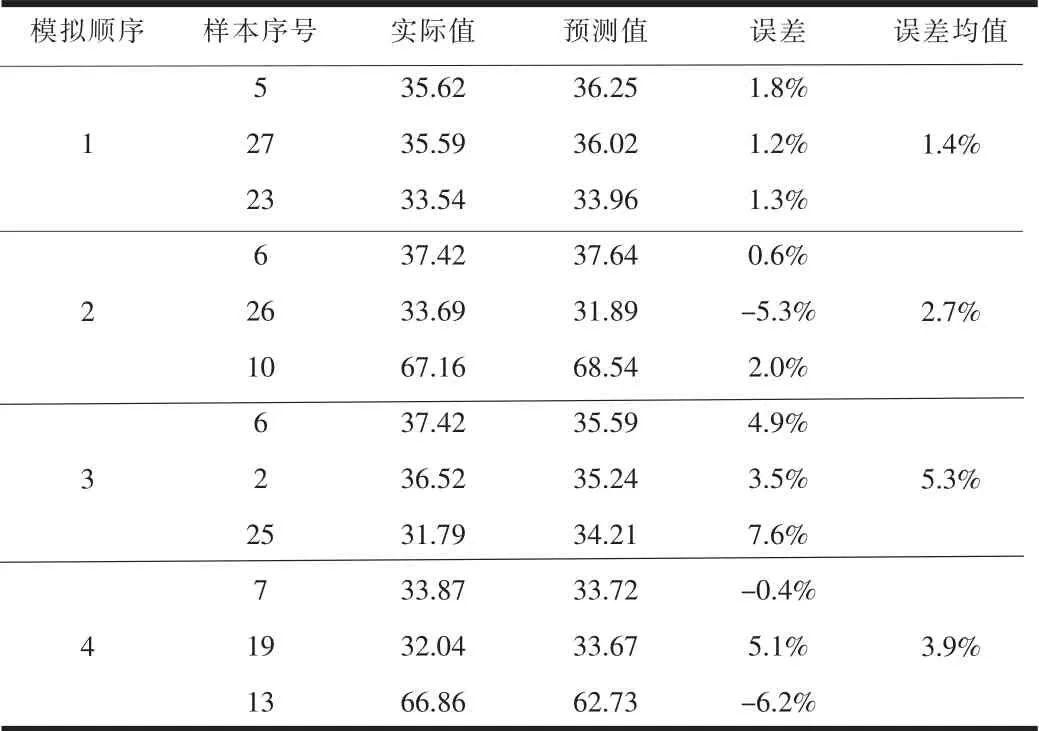
表2 预测数据分析
由表2可以看出:第1次模拟的3组数据相对误差分别为1.8%、1.2%、1.3%,误差均值为1.4%;第2次模拟的3组数据相对误差分别为0.6%、0.6%、-5.3%,误差均值为2.7%;第3次模拟的3组数据相对误差分别为4.9%、3.5%、7.6%,误差均值为5.3%;第4次模拟的3组数据相对误差分别为-0.4%、5.1%、-6.2%,误差均值为3.9%。预测值的误差≤10%,预测结果与实际值的偏离在合理范围[9],因此基于BP神经网络构建纤维土价格模型预测效果较好。
4 结语
实例证明,应用BP神经网络构建不同类型合成纤维土的价格模型是可行的。通过模型估算,可以测算在土中掺加无机结合料及纤维的单方造价,结合纤维土体积,计算出纤维土的整体造价。同时,也可以根据预测的纤维土价格反推最经济的组合,以此选择最佳纤维种类、掺比、长度,便于工程项目中的纤维土造价预算控制。
对于工程项目而言,工程造价预算准确性对企业成本控制是非常重要的,而工程中的材料价格的预算更是整个工程造价中的重要组成部分。本文介绍的是合成纤维土的价格模型预测研究,但这一模型对于其他工程材料的价格也是可以预测的。利用BP神经网络能够有效地预测材料价格走势,从而提高工程造价预算的准确性,进一步加强企业的成本控制。
