带记忆比例–积分–时滞输出滑模控制器设计

李习康,许璟,牛玉刚

(华东理工大学能源化工过程智能制造教育部重点实验室,上海 200237)

1 引言

PID控制因其结构简单、易于实现、鲁棒性好等优点,在航天[1]、电力[2]、生物医疗[3]等领域已得到了广泛地应用.尽管从功能角度看,PID控制能为绝大多数实际工程问题中提供有效的解决方案:通过比例项减小偏差,积分项来抑制稳态误差,并采用微分项来改善暂态响应特性.但在控制回路中实际使用的多是PI控制器,较少使用微分项,原因在于微分项易放大高频测量噪声,影响系统实际性能.

就反馈类型而言,PID控制可大致分为两类:基于状态反馈或者输出反馈的.在实际应用中,PID控制更多的是针对输出反馈,具有突出优点:仅需要基于测量输出、控制结构简单、便于实现.将输出反馈与状态反馈进行比较,可知:1) 状态反馈是基于全系统信息的,控制品质更优;2)在部分状态观测的情形下,只能采用输出反馈,不可避免存在控制品质折损[4].常规的输出反馈是基于无记忆机制的,仅采用当前的测量输出.由于未引入系统的过去状态信息,导致基于无记忆输出反馈机制的PID控制所适用的系统十分有限[5].针对上述问题,文献[6]提出了带记忆反馈机制,用于解决电力系统时滞问题,将当前和过去测量输出同时引入反馈回路,提高数据利用率、控制品质.文献[7]采用了带记忆的静态输出反馈控制器,基于线性矩阵不等式方法,给出了系统可静态输出反馈H∞控制的充分条件.文献[8]中设计了一种神经网络PID控制方法,解决了无刷双馈电机的转速控制问题.

另一方面,实际工程系统中不可避免地存在外部扰动或参数不确定性,这给PID控制的实际应用带来了严峻挑战.滑模控制方法是解决具有外部干扰的非线性系统的一种有效方法之一,将滑模控制与PID控制相结合,已在许多领域中得到广泛关注.文献[9]设计了具有鲁棒性的PID滑模控制器来控制电机的速度,使得在存在不确定性、非线性的外部干扰下,系统输出能跟踪上所期望的轨迹.文献[10]提出了一种带扰动估计的PID滑模控制器,用于对微机械手系统的运动跟踪控制.文献[11]设计了一种非线性PID滑模控制器,结合了无模型的PID控制器和基于模型的PID控制器的优点,实现了对仿生机器人的减振性能优化.

PID滑模控制结构灵活多变,目前主要问题仍在于滑模面中的微分项:微分项的增益选取不当,易放大高频测量噪声[12],导致系统性能退化,甚至引起失稳等严重后果[13].因此,在实际应用中,鲜少使用PID滑模控制的微分部分[14].在输出反馈控制器中,时滞常可以选为一个设计参数,用于改善闭环系统性能:平滑高频测量噪声、增强设计自由度[15–16].但时滞型控制器相对于传统控制器而言,控制参数数量更多,参数整定过程更为复杂,触发了本文的研究动机.文献[17]针对伺服系统的速度控制问题提出了一个积分–时滞型控制器,人为引入的时滞减少了测量过程中滤波器的使用.文献[18]提出了一种针对二阶系统的PIR控制器,通过几何代数分析,给出基于衰减速率的参数整定法.

本文设计了基于带记忆输出反馈的PIR滑模控制器,创新性地从频域角度分析系统稳定性与暂态响应性能.在自主设置期望衰减率的前提下,给出控制器参数自整定方法,避免了PIR控制器参数需要反复设定和调整的问题.本文所设计的带记忆输出反馈PIR滑模控制器具有以下显著优势:

1) 从控制器结构来看,采用带记忆型控制结构,不需要引入额外的观测器或者微分器来估计系统输出的微分项,用时滞项来替代传统PID滑模控制器中的微分项,通过合理选择时滞大小来改善传统控制器微分项的鲁棒性能.同时根据要求的控制性能指标设计控制参数,给定衰减速率,可以找到与之对应的控制器参数,直接从频域上构建了系统暂态性能和控制器设计之间的联系;

2) 从整定方法来看,给出了两种参数整定法,迭代消除法可根据期望衰减速率将系统极点配置在一定区域,满足系统衰减速率要求.二重极点法则可直接将系统极点配置与期望的极点附近(由于指数项的存在,系统存在无限个根),同时满足衰减速率要求来合理选择时滞参数的大小.

2 系统描述与引理

考虑以下二阶线性定常系统:

针对系统(1),传统的基于输出反馈的PID滑模面常选取为

其中:kp,ki,kd分别为PID参数.但由于系统状态不可测量,滑模面(3)不可实现,不能直接应用于输出反馈的情形.采用以下基于有限差分的微分估计方法:

将式(4)代入到式(3)中,可得以下带记忆PIR滑模面:

注1带记忆PIR滑模面(5)是滑模面(3)的可实现形式.

带记忆PIR滑模面(5)具有以下优点:1)充分利用过去时刻以及当前的信息对系统进行控制;2)不需要重新设计观测器重构系统状态,只需要系统过去时刻的值来对系统状态进行估计;3)引入时滞平滑高频测量噪声,改善系统性能[19–20].

根据泰勒公式,可知

其中O(h2)表示为h的二阶无穷小.

将式(6)代入到式(5)中,考虑到余项O(h2)是关于h的二阶无穷小[21],而h的取值通常较小,因此忽略近似误差,得

对式(7)取微分,可得

将式(2)代入到式(8)中,同时结合式(1),可得

将式(4)代入到式(10),可得下述基于输出反馈的带记忆等效控制律:

因此,可得

本文旨在设计带记忆PIR滑模控制器,改善系统收敛速率,增强系统对于不确定性、高频测量噪声的鲁棒性.

一个良好的系统通常需要具有快速的收敛特性,常以衰减速率作为性能指标进行刻画.下面给出衰减速率的定义:

定义1[22]系统具有指数稳定性,则应满足以下条件:|x(t)|≤me−σt|x(0)|,其中:m≥1,σ为衰减速率,要求σ >1.

注2σ刻画了系统动态的暂态特性,σ越大,表明系统响应速度越快.

在后文的推导中,将采用下述引理:

引理1[23]隐函数微分定理:考虑一个连续可微的函数F(x,y);定义F(x,y)=c,若方程两边同时对x取微分可得

3 滑动态稳定性分析

在控制器(12)中,存在3个待设计控制器参数ka,kb,h,本节将基于频域分析,提出两类PIR滑模控制器参数整定方法:迭代消除法和基于衰减速率的极点配置法.

迭代消除法[24–25]的核心思想是通过在变量之间增加一定的约束,在滑动态稳定性分析中增加了限制条件,并限定参数整定的可行域,连续降低系统变量的维数.基于迭代消除法,可以将系统极点配置到左半平面区域内的指定极点区域,控制器的参数选择仅与系统本身参数以衰减速率相关,从而处理控制器中因引入时滞而带来的整定困难.

下面将给出基于迭代消除法的PIR滑模控制器参数整定方法.

定理1针对系统(1)与控制律(12),对于给定的衰减速率σ,根据迭代消除法整定PIR滑模控制器参数如下

此定理的证明可以通过以下步骤形成:

步骤1闭环系统分析.将式(12)带入到系统(1)中,可得以下二阶闭环系统形式:

对方程(15)两边求拉氏变换后,可得

步骤2平移与频域变换.由于闭环系统特征方程(16)中存在指数项,方程有无限个根.为了使控制器参数整定与衰减速率相关,将变量s进行变量替换:s →(s −σ)等价于将虚轴向左平移σ个单位,从而分析闭环系统特征方程的σ–稳定性

由复域转换到频域分析(s →jω),可得

步骤3采用迭代消除法处理指数项.方程(18)的实部、虚部分别为

为了进一步分析,对式(18)求导,可得

同理,方程(21)的实部、虚部可以简化为

根据引理1,式(18)两边同时对ω取微分可得

式(18)中对σ求导可得

由式(21)与式(25)得如下关系:

将式(26)代入到式(24)中,等式成立以下两个条件满足任一即可:

结合特征方程有以下两个必要的条件:

当且仅当以下条件均成立时,上述两个必要条件满足

式(29)除以式(30)得

同理,式(33)除以式(32)得

由于式(31)和式(34)有公因式cot(hω),将式(31)除以式(34)有

步骤4求解σ.如果σ在ω域内存在极值点,那么会满足条件

再次对式(35)使用引理1:

由上式可得以下两个必要的条件:

用式(38)消去ω后得到

其次,下述定理给出基于衰减速率极点配置法的PIR滑模控制器参数整定方法:

将式(40)代入到系统(15)中并对时滞项进行如下近似:

得系统配置的极点为

此定理的证明可以通过以下步骤形成:

步骤5由于指数项的存在,系统(16)有无限个极点,根据拟多项式根查找算法[26],选择系统(16)的二重极点为−σm,这表明方程(17)满足以下两个条件:

步骤6其次,结合式(17)与式(42),可得

由式(43)可计算出控制器参数计算式(40).

4 可达性分析

在以上进行滑动态稳定性分析后,接着对滑模控制的趋近模态进行分析.选择如下趋近律[27]:

其中ε>0,ε可以取得任意小.

根据上述趋近律设计趋近模态的控制律为

其中:切换增益k>|kd|d∗,符号函数sgns用来补偿系统外部匹配扰动d(t).

定理3对于含有已知上界扰动和有界观测误差的系统,选择滑模面(7)和趋近律(44),系统状态将在有限时间T内收敛到滑模面s上,其中

此定理的证明可以通过以下步骤形成:

步骤1首先,选取Lyapunov函数为

步骤2其次,由式(7)和式(45),可得

步骤3最后,对式(46)取微分并结合式(47)得

由于V是关于时间t的函数,对上述不等式两边同时对时间t进行积分可得存在T=使得V(t)=0,对于所有的时间t>T,均有s(t)=0,因此状态可以在有限时间T内到达滑模面.

由式(48)可知选择合适的参数k,使得ε大于0,控制器(45)可使得系统(1)满足滑动模态的到达条件,即系统(1)渐进稳定.

5 PIR控制器参数自整定算法

对系统在已知上界扰动的情况下,结合滑动态分析与可达性分析过程,设计PIR输出滑模控制器,同时给出在实际PIR滑模面下的控制器形式,最终得到两种不同的控制器参数整定法:基于消除法的控制器参数整定算法(见算法1)、基于衰减速率的极点自适应配置法(见算法2).

算法1的稳定性的判定依据为:常规的连续系统判定是极点位于左半开平面时,则系统处于稳定.基于此,本文设计的方法依据论文[28]中的方法,是将闭环特征方程向左平移σ个单位,然后分析系统的σ−稳定性,即系统稳定的同时,具有一定的衰减速率.

算法1的核心内涵在于:消去了σ和h,ω的关系,将控制器参数ka,kb,h限制在一定的范围内,通过设置衰减速率,并结合系统参数,自适应计算出控制器参数.

算法2则是通过在通过极点配置,保证闭环系统的极点位于左半开平面的给定区域内,使得闭环轨迹能够指数稳定.

不同于算法1,算法2中σ和h均可以选为期望参数,h越大,平滑滤波效果越优,h越小,近似误差越小.因此可以根据工程师经验,选择一个折中效果的h.算法2直接构建了频域分析和时域设计的桥梁,可以将系统的闭环极点任意配置到期望区域.

6 仿真

为了验证本文算法对实际二阶系统的有效性,以无源RLC网络系统为例进行仿真实验.

6.1 迭代消除法仿真测试

选择由电阻R、电感L和电容C组成的无源网络[29],ui(t)为输入量,uo(t)为输出量.设回路电流为i(t),由基尔霍夫定律可写出回路微分方程为

消去中间变量i(t),便得到描述网络输入输出关系的微分方程为

令u(t)=ui(t),y(t)=uo(t),取L=0.2 H,C=5 F,R=0.8 Ω,由拉氏变换得

下面设计PIR滑模控制律改善系统性能:为了使系统具有更快的响应速度,给定衰减速率σ=3,根据算法1计算h=1,ka=−3.9,kb=−0.1.

选择理想的PID,PIR滑模面分别为

计算得到控制律

选择外部扰动为d=0.02 sin 5000t进行仿真测试,代入到闭环系统(1)中得

解此DDE[30]可得:

图1中x1为系统的实际输出,x2是x1的一阶导数,从图中可以看出在迭代消除法控制作用下系统实际输出x1将在5 s左右达到稳定状态,输出的一阶导数x2在6 s左右达到稳定状态.

图1 迭代消除法控制效果仿真结果Fig.1 Simulation result of iteration-elimination control

6.2 基于衰减速率的极点配置仿真测试

根据式(40),绘制ka,kb关于σ,h的三维图如图2和图3所示.

图2与图3分别为在给系统配置二重极点下,PIR滑模控制器参数ka,kb与待给定参数σ,h之间的关系图,从图中可以看出当固定σ不变时,随着h的不断减小,ka与kb逐渐收敛到一个定值.

图2 控制器参数ka与σ,h关系图Fig.2 Controller parameter ka and σ,h relationship diagram

图3 控制器参数kb与σ,h关系图Fig.3 Controller parameter kb and σ,h relationship diagram

下面采用基于衰减速率的方法对系统进行极点配置,首先固定σ,改变h,选择3组σ,h参数对:(3,0.1),(3,0.01),(3,0.001),同理,根据算法2分别计算得(ka,kb)的取值为(−7.18,−1.48),(−7.91,−1.94),(−7.99,−1.99).

因此,分别选择理想的PID,PIR滑模面分别为

计算得到PIR输出滑模控制律

将上述PIR输出滑模控制律代入到闭环系统(1)中,分别求解3个DDE,结果如图4所示.

图4 极点配置法仿真结果Fig.4 Simulation result of the pole configuration method

在存在测量噪声n(t)=0.02 sin(5000t)的情况下,比较不同h值对高频噪声的抑制能力.

图5中,h的取值越大对高频噪声抑制能力越强,但h取值太大,容易导致系统失稳,减小h的值后,测量噪声会被放大,因此在实际设计系统时,需根据控制需求合理选择h.

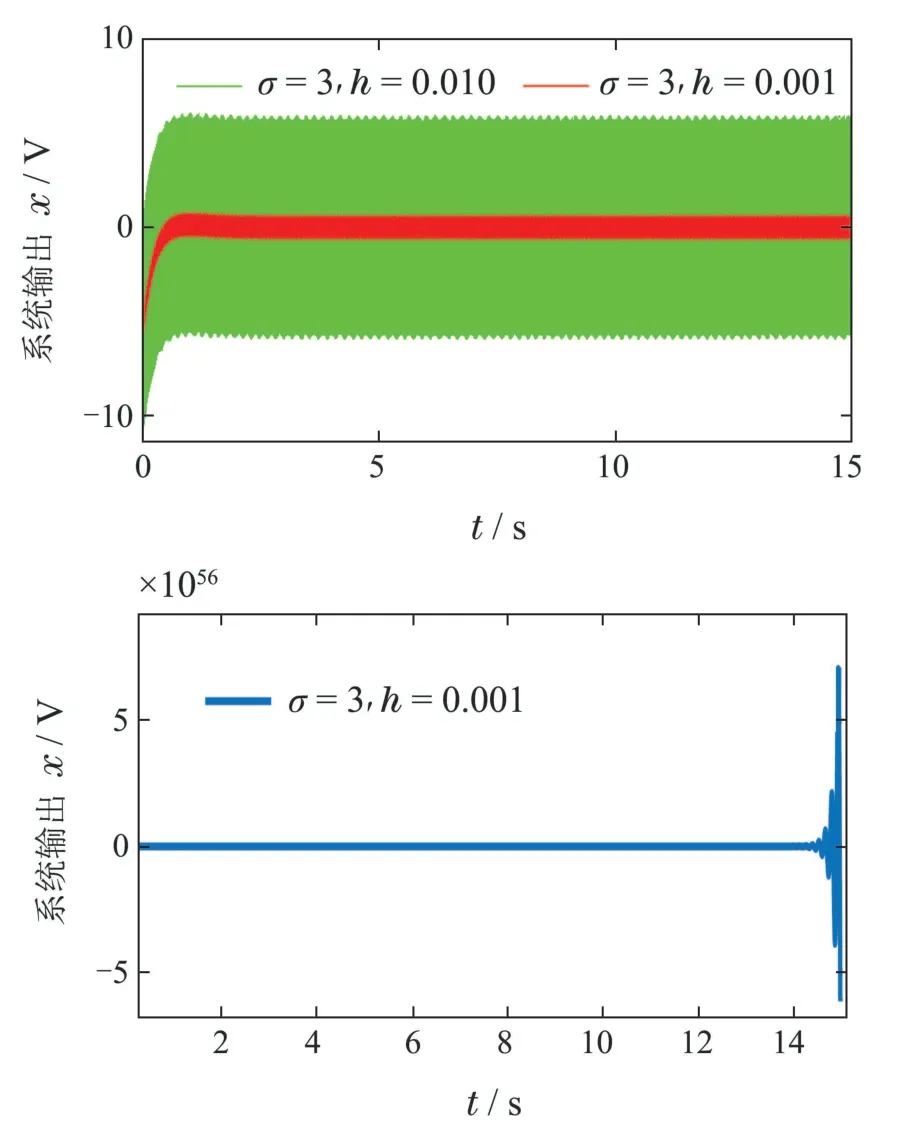
图5 不同时滞大小对高频测量噪声的抑制能力Fig.5 The ability of different delay sizes to suppress high-frequency measurement noise

下面对系统的衰减速率与给定常值的衰减速率进行对比.

图6表明系统的衰减速率处于e−2t与e−3t之间,且通过分析可知当h的取值越小时,估计误差越小,衰减速率越接近e−3t.

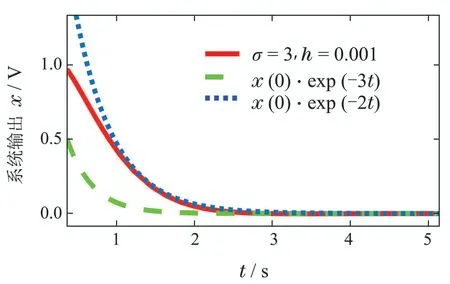
图6 指数衰减速率对比图Fig.6 Exponential decay rate comparison

7 结论

为了改进传统PID滑模控制器对高频噪声的抑制能力,本文提出一种基于频域分析的PIR输出滑模控制方案.首先,引入带记忆输出反馈,分析得到了滑动模态下的等效控制律,证明了闭环系统滑动态的稳定性.其次,基于频域分析给出两种控制参数整定算法.最后,通过构造Lyapnov函数对所设计的PIR输出反馈滑模控制器的有限时间可达性进行了分析.仿真结果表明,两种整定算法均可改善二阶系统的动态性能,增强系统鲁棒性,同时提高其抑制高频噪声的能力.