基于平方根形式的无迹卡尔曼粒子滤波的电力系统动态估计

李 明,王 凯,李晓亮,刘治国

(国网河北省电力有限公司馆陶供电分公司,河北 邯郸 057750)

0 引言

随着社会的不断发展,分布式电源、风能、太阳能等新能源不断接入,对电力系统稳定性的要求越来越高。为了提高电力系统的稳定性,必须提高电力系统调度、控制、安全评估等方面的能力。电力系统动态估计是电力系统调度、控制、安全评估的基础,动态估计通过状态预测能对电力系统进行安全评估,实现经济调度、预防控制等在线功能,重要性不言而喻,鉴于此,必须快速、准确地对电力系统进行动态估计。

20世纪70年代初,Debs等人提出了卡尔曼滤波算法,并用最简单的系统模型建立动态状态估计,卡尔曼滤波处理的是线性问题,而电力系统的动态估计属于非线性问题,此方法的状态估计精度低。然后引出了扩展的卡尔曼滤波算法[1- 2](EKF),扩展的卡尔曼滤波算法处理非线性系统的思想是将非线性函数在估计点附近进行泰勒级数展开,并用一个等价于常规卡尔曼滤波方程的近似矩阵来代替非线性函数。此方法的估计精度较低,然后又引入了无迹卡尔曼滤波算法[3-5](UKF))来进行状态估计,无迹卡尔曼滤波也是最小方差估计器,核心思想是无迹变换。如将非线性方程采用泰勒级数展开式表达,可以看出无迹卡尔曼滤波算法能够精确到与三阶泰勒级数展开式相当的均值和方差。

但EKF和UKF都是针对非线性系统的线性卡尔曼滤波方法的变形和改进,因此受线性卡尔曼滤波算法的条件制约。粒子滤波[6-9](PF)能够很好的进行非线性系统的状态估计,在一定程度上提高了状态估计精度,但是PF选择转移概率密度作为重要性密度函数,在计算重要性概率密度函数时没有考虑到最新的量测信息[10],当预测先验与似然函数重叠少或者量测模型密度较高时,可能偏离真实的后验分布,导致粒子滤波存在着退化现象和粒子匮乏问题。传统动态估计方法在含有间歇性、波动性较强的新能源系统中,适应能力和稳定性较差,状态估计精度较低。

针对这些问题,引入了无迹卡尔曼粒子滤波的算法[1114](UPF),UPF在非线性或者非高斯分布的贝叶斯估计等方面得到了很好的应用,可以有效解决状态估计问题。

基于电力系统动态估计,提出了平方根形式的无迹卡尔曼粒子滤波(SR-UPF)的状态估计方法,无迹卡尔曼滤波作为概率密度函数引入到粒子滤波中可以有效解决粒子滤波中存在的退化现象,在粒子滤波过程中,使用Mar kov链蒙特卡罗方法保持粒子的多样性,有效解决了粒子匮乏的问题,本方法还保障了滤波收敛速度和稳定性,能够很好的应用在含有新能源接入的电力系统中。为了减少计算时间,本文还适当的减少了粒子个数,并通过IEEE 14节点系统进了仿真验证,表明SR-UPF在不牺牲大量计算时间的情况下,可以有效提高状态估计的精度。

1 电力系统动态状态估计模型

对于电力系统动态状态估计问题,非线性系统的动态模型和量测模型表达如下

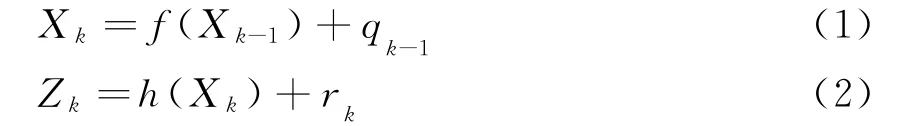
式中:Xk为k时刻的n维状态向量,Xk=[Vk,θk]∈Rn为节点电压的幅值和相角;Zk为k为时刻的m维量测向量,Zk=[Pk,Qk,Vk,θk]∈Rm为节点的有功功率、无功功率、电压的幅值和相角等;f(·)为k-1时刻的状态向量转移函数;h(·)为k时刻的量测方程,量测模型采用混合量测;qk～N( 0 ,Qk)为系统噪声;rk+1～N( 0 ,Rk+1)为量测噪声。

动态估计的基本原理:假设在k-1时刻已经求的状态估计向量X^k-1,要求在量测到k时刻量测量Zk后,求出该时刻的状态向量X^k,估计的准则是以状态向量估计误差方差阵Pkk最小为目标函数,即

式中:ekk=Xk-X^k=Xk-Xkk,Xk,为k时刻状态变量的真值,X^k=Xkk为k的状态估计值。

2 改进SR-UPF的电力系统动态状态估计

为提高动态估计的精度,解决粒子滤波中存在的粒子退化现象和粒子匮乏问题,在粒子滤波中加入了重采样和选择合理的建议密度来解决上述问题。无迹卡尔曼滤波非常适合做建议密度函数,所以导出了无迹卡尔曼粒子滤波的电力系统动态估计。

UKF改进的粒子滤波算法的核心在于,在采样阶段,可以利用UKF算法为每个粒子计算其均值和协方差,然后利用该均值和方差来指导采样。在基本的粒子滤波的基础上还加入了利用Markov链蒙特卡罗方法保持重采样后粒子的多样性。最后提出SR-UPF的电力系统动态估计,保障了状态估计的稳定性,有效提高了状态估计精度。

2.1 粒子初始化

在粒子滤波的电力系统动态状态估计中,需要对代表电网节点状态的粒子进行初始化。在对粒子进行初始化时,如果已有电网节点的状态量,则以节点状态量为均值,符合高斯分布来产生粒子集合;如果不知道电网节点的状态量,则在可能的状态量范围内产生均匀分布的粒子集合。

粒子数量N由要求的计算精度和计算资源决定,理论上N越大,得到的估计越准确,当N趋于无穷时,能准确估计电网状态;但N越大,计算量越大计算时间也越长,应根据所需计算速度和计算精度选择合适的粒子数量。初始化时每个粒子所有节点权重都赋等值。

式中:ωmk代表k时刻m粒子的权重。

2.2 UKF更新粒子

2.2.1 UT变换

2.2.2 UT变换的采样方法

2.2.3 利用Mar kov链蒙特卡罗方法保持粒子多样性

2.3 基于SR-UPF的电力系统动态估计

图1 SR-UPF的动态状态估计流程

步骤5,粒子分裂,进行权值调整并归一化。

步骤7,利用Mar kov链蒙特卡罗方法保持重采样后粒子的多样性对更新后的粒子进行权重归一化,得到粒子最新权重ωi(k)。

步骤8,计算得到电力系统的状态估计值,计算公式如下

步骤9,判断是否达到终止条件,满足则终止,否则,k=k+1,返回步骤3计算下一时刻状态估计值。

3 算例分析

使用均方根误差(Root mean square error,RMSE)作为性能指标函数。k时刻的均方根误差公式为

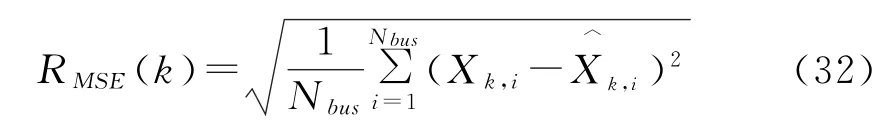
本文在IEEE 14节点系统上进行了数值试验。在此系统中节点3和节点5为分布式电源,仿真中以系统潮流计算结果为真值,量测数据通过在测试系统潮流结果的基础上叠加相应的正态分布随机量测误差而形成,其中SCADA系统量测误差的标准差是0.02,均值为0;PMU电压幅值量测误差的标准差为0.005,均值为0,相角量测误差的标准差为0.002,均值为0;粒子更新所用到的静态数据参考了文献[7]。UPF中的参数选择:k=0,β=2,α=0.01,粒子个数通过试验选取。

为了研究不同数量的粒子对本文所提算法状态估计精度的影响,在IEEE 14节点的电力系统进行了仿真试验,仿真结果如表1所示,其中ξθ代表电压幅值的均方根误差,ξv代表电压相角的均方根误差。

表1 不同粒子个数的仿真比较

由表1结果可得,SR-UPF状态估计的精度会随着粒子数目的增加而增加,但SR-UPF在提高估计精度的同时存在着计算量不断增加,计算时间增加的问题,本文在保障估计精度的情况下,尽量减少计算时间,选择了粒子个数N为150个。

对于IEEE 14节点系统,表1对几种算法的性能进行了对比,图2-图6显示任意选取节点1的估计值与真值曲线、整个系统的性能指标RMSE和计算时间对比。

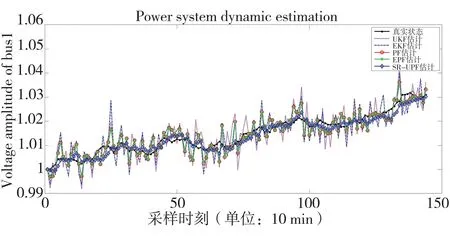
图2 IEEE 14节点1的电压幅值估计值与真值

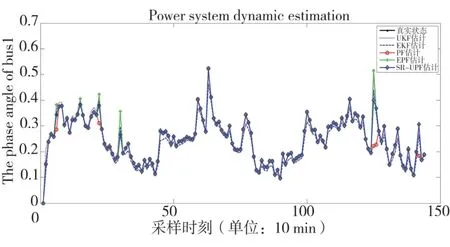
图3 IEEE 14节点1的电压幅值估计值与真值

图4 IEEE 14幅值估计的RMSE

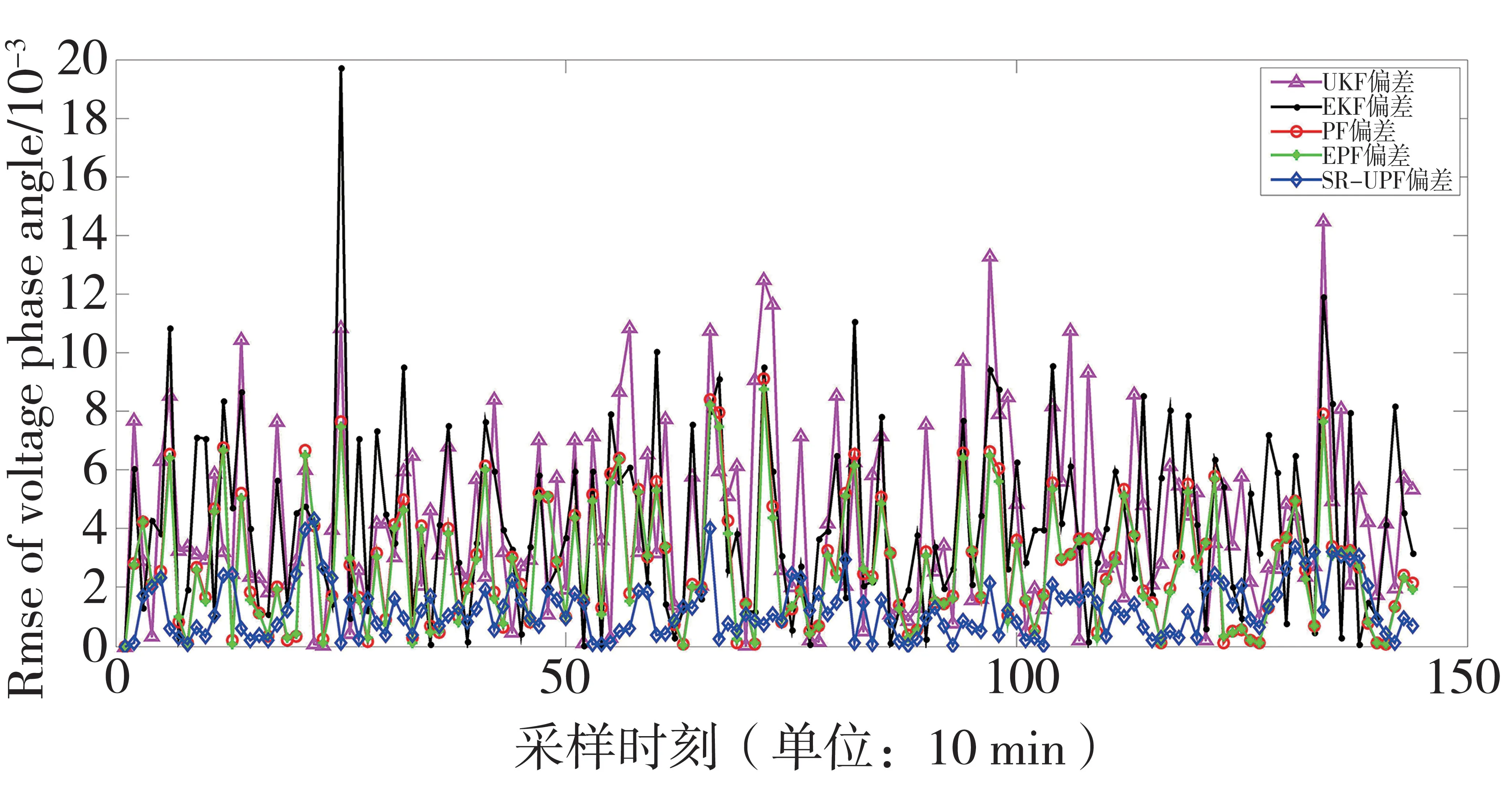
图5 IEEE 14相角估计的RMSE

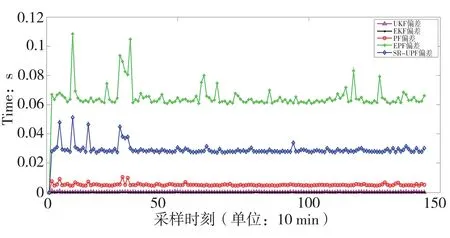
图6 IEEE 14不同方法的计算时间对比

表2 IEEE 14系统中5种算法的性能比较

通过以上仿真结果表明,本文所提的状态估计方法虽然牺牲了少量的计算时间以及在个别采样点的均方根误差较大,但是该方法的平均均方根误差最小,在整体的状态估计上表现出巨大的优势。通过以上分析可以得出本文所提的方法可以有效的提高电力系统动态状态估计的精度。

4 结束语

建立了SR-UPF的状态估计方法,经过仿真验证,PF与EKF、UKF算法进行比较,PF估计精度有所提高,但是PF存在着粒子退化和匮乏的问题,以上传统方法在含有间歇性和波动性的新能源电力系统中估计稳定性差,精度低。本文所提的SR-UPF方法解决了粒子退化和匮乏的问题,保障了状态估计的稳定性,有效提高了状态估计的精度。但是SR-UPF与EKF、UKF相比,计算耗费时间略长,对于此问题接下来还需要继续研究。