浅析一种判断自动化设备状态稳定性的新方法

卢国志，胡斐，倪萍

（山东科技大学，山东 青岛 266590）

在工业生产中，设备是否能安全、稳定地运行一直是一个重要问题，随着设备的重要程度增加，其故障可能带来的损失也就越大。工业设备正常运行的关键要素是维护和检修，包括事后检修、计划检修和状态检修。由于很多大型安全生产事故的发生，其原因往往仅仅是由于某一关键设备的带“病”作业，小问题逐渐引起细微的性能变化，从而引发大事故。因此，企业能做的除了事后维修外，更要加强以预防为主的检测，提前识别出设备的细微变化，从而将事故扼杀在摇篮中。为了能够更有效地进行预防性的检测，需要对设备的运行状态进行评估，传统的状态评估主要是基于理论分析以及物理模型分析，但由于设备故障影响因素众多、机理复杂，难以建立完善、精确的状态评估物理模型。近年来，随着传感器技术、数据收集与处理技术的发展，大数据技术在工业设备故障诊断的广泛应用，通过数据判断设备状态，即数据驱动成为许多企业选择发展的方向。本文在数据驱动的基础上，提出了一种新的状态评估数据处理方法，并称为“数据切片”。

1 基于大数据的设备状态判断模式

1.1 传统模式

针对设备的状态预警判断离不开对数据的处理分析，一般数据处理思路可概括为四步：标准化处理、预警阈值确定、异常点筛选、原因分析。如图1所示，为某设备中四处监测数据，根据每组数据的波动情况合理设置预警阈值以及异常检测的强弱，临近预警阈值则需要警戒，超过预警阈值则需要停止运行并检修，之后通过不同数据间的组合来分析确定故障的原因。然而，当数据种类增多时，影响数据的因素增多，仅仅用单一数据的异常点来判断是否存在故障的准确率和效率都较低，而综合考虑数据之间的关系建立复杂模型又对专业性的要求较高，导致实用性不足，因此，本文提出了一种数据切片模式，既能满足综合考虑不同数据，又能降低专业性的要求。

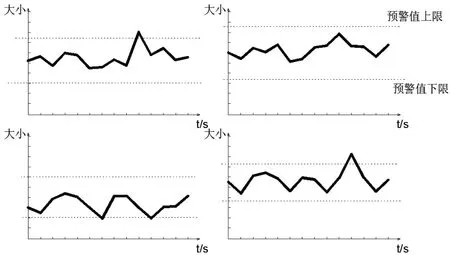
图1 阈值预警图

1.2 数据切片模式

数据切片即通过假想一个时间维度的切片，将某一设备的运行状态通过切分分成无数个仅与时间相关的状态，每个状态则由多个状态参量进行表示，同时，按照设定的处理方式将每个状态的多个状态参量值用一组坐标代替，并放入坐标系，之后通过聚类等方式对其分组并找出异常点。

1.3 数据切片相关定义

定义1：状态参量：在某一确定时刻，用来表示机器该时刻运行状态的参数，记作ki（i=1，2，....，n）。例如，可以用某时刻人体的血压、体温、血糖、血脂、尿酸、总胆固醇等参数来确定该时刻人的健康程度。

定义2：状态特征曲线：由n个状态参量构成的可以代表设备t时刻运行状态的曲线。

定义3：状态坐标系：由状态特征曲线中n个状态参量值通过三种函数变换得到的三个值，从而组成三维坐标系中的x，y，z轴。

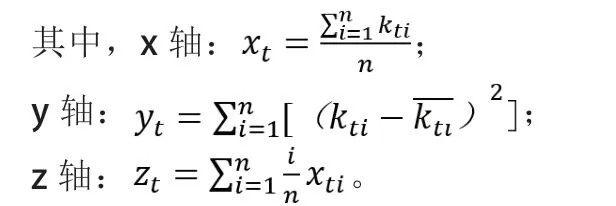
式中，x轴表示在t时刻下的n个状态参量的均值；y轴表示在t时刻下的状态特征曲线的波动情况；z轴用来区别t时刻下状态曲线的变化方向。通过（x，y，z）可以将任一时刻下的机器运行状态用空间中一点代表，每个点均只对应一种状态曲线。状态坐标系的确定规则可以针对不同设备的特征进行修改，以便聚类分析。

2 具体步骤

根据上述介绍，基于数据切片模式判断设备状态稳定性的流程主要包括以下四步：（1）数据预处理；（2）获得状态曲线；（3）确定状态特征值；（4）聚类分析，具体流程如图2。

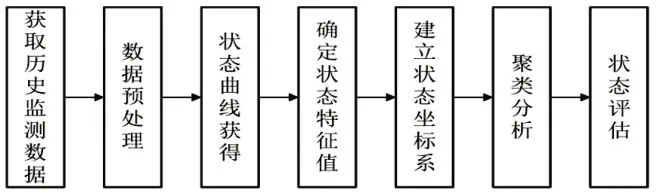
图2 数据切片流程图

2.1 数据的归一化

在多指标评价体系中，由于各评价指标的性质不同，通常具有不同的量纲和数量级。当各指标间的水平相差很大时，如果直接用原始指标值进行分析，就会突出数值较高的指标在综合分析中的作用，相对削弱数值水平较低指标的作用。因此，为了保证结果的可靠性，需要对原始指标数据先进行归一化处理。在此，本文提供两种数据归一化的方法。分别为：

（1）线性函数归一化：也称为离差标准化，通过对原始数据进行线性变换，使得结果映射范围在0～1。其转换函数为：。

（2）0均值标准化：这种方法是结合原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。使处理过的数据符合标准正态分布，即均值为0，标准差为1。其转换函数为：。

其中，Mean为所有样本数据的均值。Standard deviation为所有样本数据的标准差。

2.2 数据状态曲线的获得

通过归一化处理，可以获得n×t个在0～1（或符合正态分布）的数据，将其放入坐标系中如图3所示，其中三个轴分别为数据种类、时间、大小，在将各个数据点生成曲线后，构想一垂直于时间轴的平面作为切片，该平面与各类数据曲线均有一个切点，连接所有切点得到一条曲线称为数据状态曲线。之后通过左右平移该平面，可获得各个时间节点的数据状态曲线。

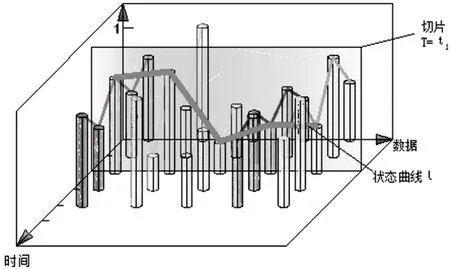
图3 状态曲线图

2.3 数据状态特征值

根据定义3，采取合理的处理规则，对状态曲线进行处理后，每条状态曲线可用三个数字表示，分别作为x、y、z三轴坐标放入空间坐标系中，可获得t个空间中的点，如图4。

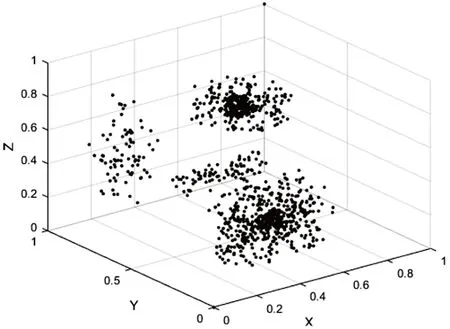
图4 数据集可视化

其中，X、Y、Z三轴分别为按照特定规则处理后的状态坐标系，坐标系中的每个点则代表了一条状态曲线。

2.4 聚类分析发现异常点

聚类分析方法是在数据挖掘中常用的一种方法，按照欧氏距离或者马氏距离等距离法对数据进行聚类，通过聚类结果，可以将原数据分成距离较小的较为相似的簇，在本文中将属于某一簇的数据认为是正常点，不属于任何一簇的点认为是异常点，对该点进行追溯找出其发生的时间，通过异常发生时间便能对机器的稳定性运行提供帮助。由于马氏距离能够排除变量之间的相关性的干扰，故此采用马氏距离。

式中，D(Xi，Xj)指的是样本之间的马氏距离，T指的是转置操作，S指的是样本协方差矩阵。根据3.3中状态特征值组成的空间散点图，通过密度聚类算法对所有点进行划分类簇，其具体流程如下。

密度聚类算法过程如下：步骤1导入数据样本集合A；步骤2输入参数可达半径Eps和邻域密度阈值minpts；步骤3由数据样本集合A中任意一个未被标记的点p开始，探索点p的Eps邻域，如果在邻域内的点数目大于或等于邻域密度阈值minpts，则将点p标记为核心点，建立一个新的类簇C(p)，否则，将p点标记为噪声点；步骤4访问所有核心点，将核心点p的Eps邻域内的所有点都归入类簇C(p)中；步骤5遍历C(p)中所有没有被扫描的点q，如果点q的Eps邻域内点的数目大于或等于邻域密度阈值minpts，则将点q和它Eps邻域内的点归入类簇C(p)；步骤6访问数据集A内的所有样本，重复步骤（3）至步骤（5），直到所有样本都被处理。根据上述6个步骤，可以将空间内所有聚类簇的核心点找出，并将各点进行归类，可以看出不同簇的范围，同时，能够判断出不属于任何簇的异常点。

3 结语

本文提出一种将多维时序数据组成的曲线转换成三维空间点，并通过聚类分析判断出异常点，从而评估设备的运行状态的方法。此方法可将庞大的设备时序数据转换为空间中的点，再通过空间聚类的方式将这些点进行分类，从而筛选出异常点，从而快速察觉设备运行中潜在的异常。

本文将所描述的方法称为数据切片技术，该技术具有以下几点优点：（1）能够综合考虑多个维度的数据，将复杂的多维数据降为三维，并能够根据数据特征自行确定降维规则，有针对性地提高聚类的准确性。（2）通过该方法可以迅速从庞大多样的数据中发现异常数据发生的时间，从而进行快速反应，并且具有一定的提前性。（3）与机理建模方式相比，不需要建立复杂的物理模型、机理分析，对专业性的要求不高。（4）通过该方法可以对自动化设备的稳定运行监测提供保障，从而有效地避免潜在故障。