基于支持向量机理论的短期负荷预测

邹超，卢霁明

（1.中国电建集团昆明勘测设计研究院，云南 昆明 650000；2.云南能投电力设计有限公司，云南 昆明 650000）

0 前言

电力系统短期负荷预测是电力系统安全和经济运行的重要依据。随着价格竞争机制引入电力系统形成电力市场后，对短期负荷预测的精度和响应速度都提出了更高的要求。虽然电力系统负荷预测的研究已有多年，形成了很多负荷预测的理论和方法[1-3]，但是随着负荷预测新理论和新技术的发展，对负荷预测新方法的理论研究仍在不断地发展[5-6]。支持向量机理论作为数据挖掘的一项新技术，应用于模式识别[4,7]和处理回归问题等领域。本文利用支持向量机理论良好的非线性学习及预测特性，针对电力系统短期负荷预测的各种影响因素的非线性[8-9]特点，研究基于支持向量机理论的电力系统短期负荷预测方法[10-11]，具有重要的理论意义和实用价值。

1 负荷预测的样本选择及预处理

基于SVM的电力系统负荷预测问题的核心是寻找一个具有广泛适用性的从影响负荷的因素到负荷的映射。实际上利用智能算法构造的负荷预测模型的性能取决于历史负荷数据的数量和质量[12]。基于机器学习方法的SVM需要先对训练样本进行训练，然后用训练好的网络进行预测，而预测模型的精度和泛化能力极易受样本输入变量的影响，因此，输入变量的选择问题成为电力系统负荷预测数据预处理的关键[13]。数据的全面性对预测的效果至关重要，本文数据选择East-Slovakia Power Distribution Company提供的电网运行数据作为研究对象，即该数据包括1995—1998年这4年及1999年1月份每天的日平均气温。根据1997、1998年及1999年1月份每天24h内30min等间隔负荷采样数据，将1997、1998年历史数据作为训练样本，将1999年1月份数据视为未知数据，进行1999年1月份的日最大负荷预测。

1.1 样本的特征选择

电力系统短期负荷预测是一个多变量预测问题，它被作为函数回归问题研究。预测负荷值y为函数的输出值，而相应的影响负荷的因素如：历史负荷、温度信息、气象信息等，作为函数输入值x。训练数据的每个成分即是SVM的特征量（样本集(x,y)的输入向量x中的每一个元素称作一个特征）。不同的数据序列影响模型的方案，从而结合相关性的大小和数据决定输入样本的模型。本文选择的数据特征量为：负荷时间序列、时间因素以及气温对负荷的影响等。

1.2 训练和测试样本的确定

针对基于SVM的电力系统短期负荷预测算法中特征选择问题，许多的研究者做了很多的工作并运用多种方法来确定样本的特征量。主成分分析（principle component analysis，PCA）作为目前常用的解决输入变量选择问题的方法[14]，在理论和应用上都相对简单易懂。不仅可以压缩样本空间和提升预测的效率，也能消除由于变量间存在相关性导致的预测模型泛化能力的降低，从而有效提高模型的预测精度。

本文根据以前的研究者所做的工作，在对历史数据进行分析后，确定如下样本输入量：

1）预测日之前7天每日日最大负荷数据L={l1,l2,l3,l4,l5,l6,l7}；

2）预测日的日平均气温T；

3）预测日的周属性W=（1,2,3,4,5,6,7），其中的数值对应于周一到周日；

4）预测日的节日属性F=（1.0,0.0），其值为1表征预测日为重大节假日。

输入样本为10维的向量{l1,l2,l3,l4,l5,l6,l7,T,W,F}，对历史数据进行平滑和归一化处理，构成包含723个样本的样本集。

1.3 负荷预测步骤及预测评判标准

1）将历史样本进行归一化处理，构成SVM训练样本集；

2）根据训练样本集建立如式(1)的目标函数[15]；

对偶最优问题：

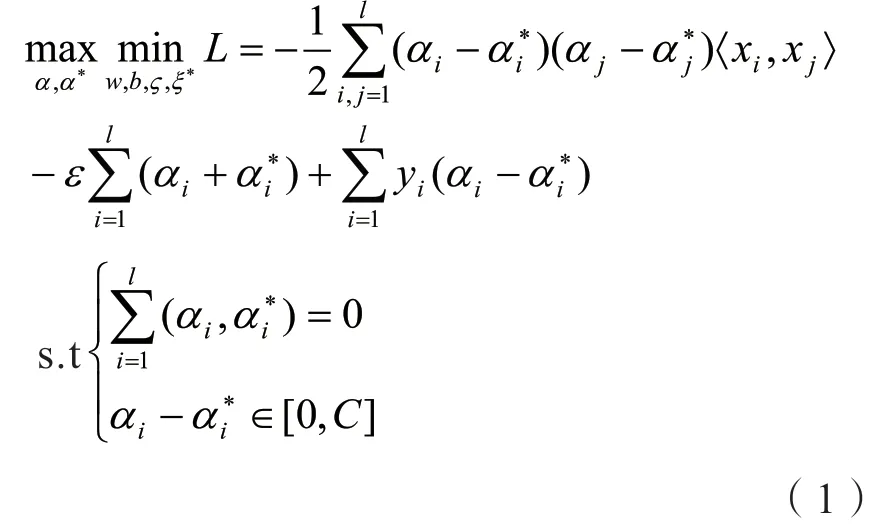
引入核函数解上式得：

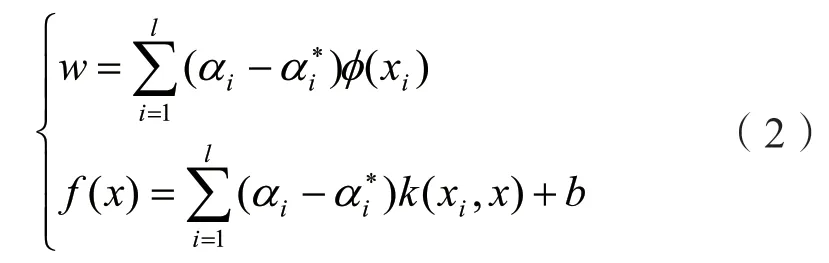
阈值b可通过下式计算得到：

3）将数不敏感损失参数ε、惩罚系数c和核函数中的宽度参数σ2代入式（1），并求解αi、α*i；

4）将αi、α*i代入式（4），用预测样本完成对次日日最大负荷的预测；

5）预测完成后，将次日负荷真实数据视为已知数据，依次完成全月的负荷预测。为验证算法的有效性，本文取平均相对误差作为预测效果评判依据，即：

式中：A(i)和F(i)分别表示实际值和预测负荷值。

2 负荷数据的归一化问题

在获取所有的训练样本和测试样本后，由于以下因素，通常要对输入的样本数据进行归一化处理：

1）避免较大范围变化的数据淹没较小范围变化的数据。

2）避免计算中出现数值困难，原因是核值计算中需要计算特征向量的内积，如线性核和多项式核等，大的特征值可能会引起数值困难。

本文中归一化是按照维来进行的，即将10维输入向量的每一维都归一化到所需的区间内。假设当前维在所有样本上的最大值是max，最小值是min，则可以作如下线性变换：

x、y分别为变换前、后的值max(value)，和min(value)分别为样本的最大值和最小值，这样就把[min,max]区间映射为[0,1]区间了；同理，也可以将数据通过规范化的映射到区间[-1,1]，此过程可由matlab的归一化函数完成。

3 核函数选取及参数优化方法

核函数的选择对负荷预测的精度有很大的影响。根据相关研究，本文选择RBF作为SVM的核函数。通过大量实验研究发现，核函数中的宽度参数σ2和惩罚系数c，对SVM的性能表现起着非常重要的作用[16]。

SVM的参数选择对模型性能有很大的影响，目前SVM的参数选择还没有公认有效的结构化方法。本文由于训练样本的数据量较大，只对对SVM的性能表现非常关键的两个参数进行寻优，即核函数中的宽度参数σ2和惩罚系数c。为确保计算的效率和实用性，本文采用网格搜索(Grid-search)和交叉验证法(Grid-search)对核函数中的宽度参数σ2和惩罚系数c进行选择。

交叉验证(Cross Validation，CV)是用来验证分类器的性能的一种统计分析方法，基本思路是把在某种意义下将原始数据(dataset)进行分组，一部分做为训练集(train set)，另一部分做为验证集(validation set)，先用训练集对分类器训练，再利用验证集来测试训练得到的模型(model)，以此作为评价分类器的性能指标。常用的CV方法为k倍交叉验证(k-fold Cross Validation)，记为k-CV。交叉验证和参数寻优是两个步骤，它们的关系是，在参数寻优的过程中，每次得到一个新的参数值，都需要用交叉验证去验证。

本文的思路是在宽度参数σ2和惩罚系数c组成的二维均匀划分的网格上确定最优值。在用SVM进行负荷预测的参数寻优和交叉验证过程如图1、图2所示。

图1 交叉验证的第一次迭代过程

图2 交叉验证的第二次迭代过程

运用SVM对本文实例分别对选择参数后和未选择参数两种情况下进行负荷预测，其结果如图3和图4所示。

由验算结果可以得出结论，使用优选参数后的预测精度显著提高，参数的选择对负荷预测效果有较大的影响。现将基于SVM的电力系统负荷预测结果与真实结果绘于图4，经计算eMAPE=1.8937%，精度较高。

图4 未选择参数预测结果比较

4 结束语

本文着重研究了SVM方法负荷预测模型中非常关键的样本选择及预处理问题。通过对所选历史负荷数据与预测负荷数据相关性的研究，为样本输入特征量的选择提供依据，并给出了样本集选择方案。此外，本文还研究了数据预处理、核函数构造及选取、参数优化的方法、数据归一化的处理等其他问题，并采用实例分析各样本处理情况下基于SVM的短期负荷预测的结果。研究表明，应用SVM进行电力系统负荷预测，具有精度高、速度快等优点，显著提高了负荷预测的效果。