基于PCA-IPSO-RBF神经网络的沥青路面破损状况预测

马 子 媛， 李 海 莲*,2， 蔺 望 东

(1.兰州交通大学 土木工程学院，甘肃 兰州 730070；2.兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州 730070 )

0 引 言

近年来，我国公路建设事业迅速发展，仅“十三五”期间公路建设就达4.2×105km，公路规模和运输量均位居世界前列．然而，随着路面使用时间的增加和人们出行频率的迅速增长，沥青路面出现大量的损毁和病害现象．当路面发生损坏后，若没能及时采取有效措施进行养护和修复，严重时将影响路面结构性能，进而对路面行车安全产生严重威胁[1-2]．因此，建立精确合理的路面破损状况预测模型可以有效避免由于路面破损造成的事故，同时还可以为养护决策的科学开展与养护资金的合理分配提供理论基础．

现有研究表明，神经网络模型可以对沥青路面使用性能进行评价和预测．常用的神经网络模型包括BP神经网络模型、灰色神经网络模型、模糊神经网络模型以及RBF神经网络模型．周鹏飞等[3]将BP神经网络应用到路面使用性能评价中，该模型有较强的泛化能力，然而针对路面使用性能评价的复杂非线性问题，其收敛速度较慢，难以推广；陈仕周等[4]提出利用模糊神经网络模型耦合遗传算法对路面使用性能进行预测，其建模所需数据量少，且短期预测精度较高，但对中长期的数据预测精度不佳，而且考虑的指标较为单一；赵见龙等[5]采用小波模糊神经网络对路面性能进行预测，由于模型数据积累量少，尚需进一步修正和完善．

基于上述相关研究的不足，本研究采用改进粒子群优化算法对径向基神经网络参数进行优化，通过主成分分析法建立考虑路面性能、路面使用状况和路面环境状况的多维沥青路面破损状况预测模型．

1 PCA、PSO、RBF神经网络基本原理

1.1 PCA

主成分分析(principal component analysis，PCA)法是将相互之间存在相关性的变量转化为几个少数线性无关变量的一种数据分析方法[6-8]．主成分分析以其强大的数据提取能力在保留主要信息的同时，将其转化为少量线性无关、具有综合性的指标变量．通过减少神经网络输入层节点个数，缩小神经网络规模，提高神经网络的泛化能力．PCA既简洁、准确又确保了信息的完整性，达到科学高效地解决研究问题的目的．

1.2 PSO

粒子群优化(particle swarm optimization，PSO)算法是一种模拟鸟群捕食的仿生学算法[9]．在PSO算法中每一个粒子都代表待优化问题的一个可能解．粒子在迭代寻优过程中，通过计算适应度比较当前位置是否为最优位置，从而决定是否需要对粒子个体最优解和全局最优解进行更新．同时粒子根据自身速度和位置信息，不断调整运动方向与路径，从而得到个体在空间中的最优解，最终得到满足终止条件的种群最优解．

设寻优问题的空间维数为n(1≤d≤n)，空间中存在m个粒子，用向量Xi=(xi1xi2…xin)表示第i(1≤i≤m)个粒子当前位置，用向量vi=(vi1vi2…vin)表示其当前速度．在满足终止条件内，通过比较粒子个体所飞行的各个位置的适应度确定第i个粒子的最优位置为Pi=(pi1pi2…pin)，进而确定整个粒子群的最优位置Gi=(g1g2…gn)．按照式(1)、(2)分别计算第i个粒子的第d维速度和位置[10]：

(1)

(2)

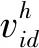
1.3 RBF

径向基函数(radical basic function，RBF)神经网络是一种3层前馈分析网络，由输入层、隐含层和输出层构成，是一种较理想的非线性计算工具．RBF神经网络的结构如图1所示，其通过径向基函数[11]控制隐含层节点进行高维非线性变换．

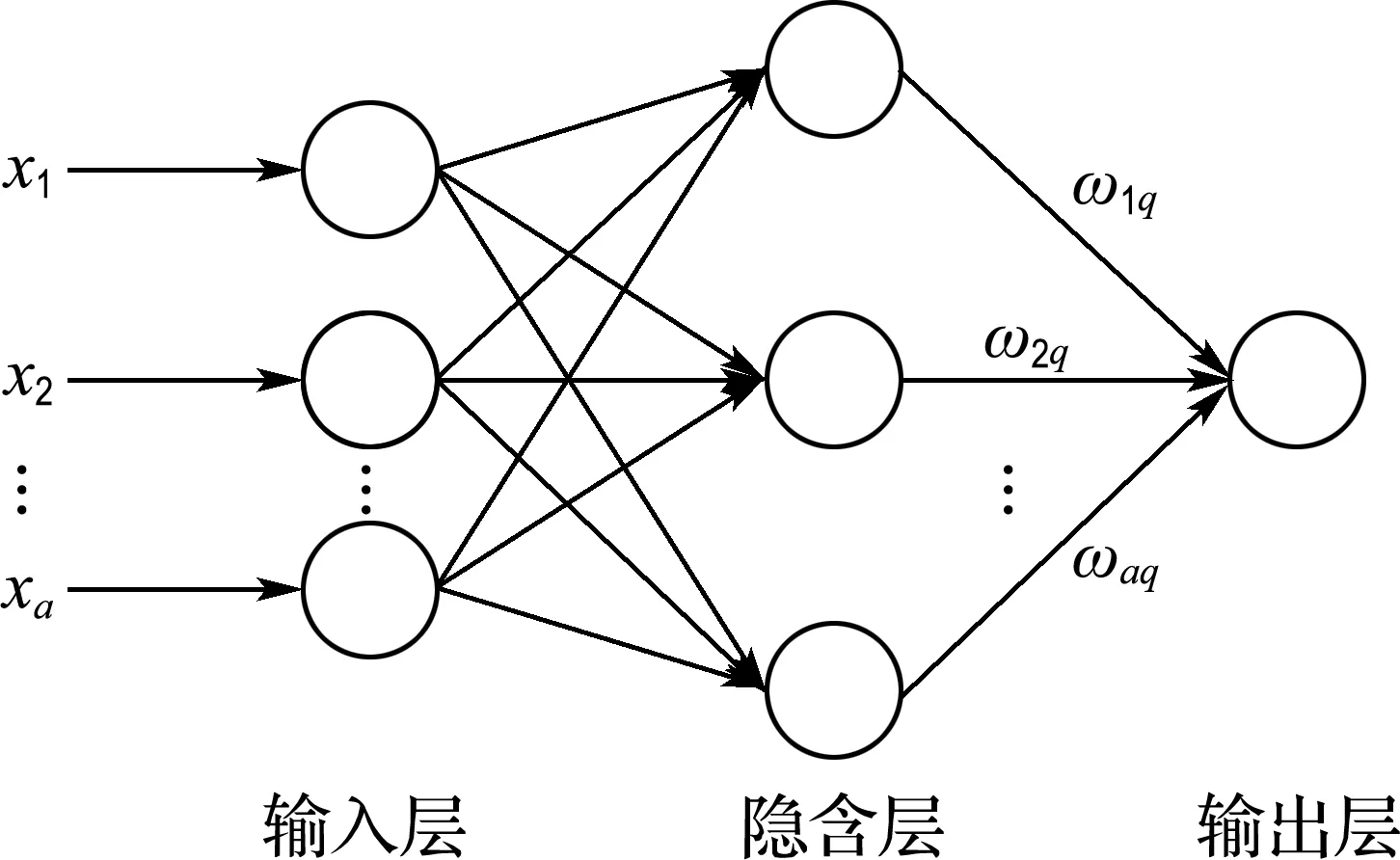
图1 RBF神经网络模型结构Fig.1 The structure of radical basic function neural network model

设RBF神经网络输入层有a个节点，隐含层有l个节点，输入层用向量(x1x2…xa)T表示，隐含层径向基函数选择常用的高斯函数[12]，如式(3)所示，则RBF神经网络的第q个输出节点表示为式(4)．

(3)

(4)

2 改进PSO(IPSO)算法优化RBF沥青路面破损状况预测模型

2.1 惯性权重因子的改进

惯性权重因子在粒子全局寻优过程中是一个重要的可调整参数[13]．传统粒子群改进算法中惯性权重因子的计算通常采用线性递减的方式，具体计算公式为

(5)

式中：ωmax和ωmin分别表示权重最大值和最小值，k表示当前迭代次数，kmax表示迭代次数的最大值．

对于一些复杂的问题，采用线性递减的惯性权重计算方式不能如实反映粒子的实际搜索过程，并且当粒子位于局部极值点邻近区域时，由于ω线性递减，容易造成粒子陷入局部最优解，使算法无法达到理想的寻优能力．相关学者的研究表明，惯性权重采用凹函数的递减方式时计算结果较为精确[14]．因此，为了更好地平衡粒子局部和全局的搜索能力，本文采用动态调整的方式对惯性权重进行改进，即采用非线性递减策略．改进后的惯性权重计算公式如式(6)所示．在粒子迭代过程前期惯性权重因子采用加速递减的方式，能够使粒子跳出局部较差的区域，逐渐向最优解方向移动；而在迭代过程后期，粒子运动速度的减小逐渐放缓，并趋于最终权重，有利于粒子在最优解邻近区域内进行局部寻优．

(6)

根据以往的研究结果[15]，ω的取值区间通常为[0.4，0.9]．

为了验证IPSO算法的寻优能力，本文利用Sphere和Rosenbrock标准函数对惯性权重采用线性递减方式的PSO算法和本文的IPSO算法进行仿真验证测试．各个测试函数的表达式、维数、搜索空间以及目标解如表1所示．

表1 两个标准测试函数Tab.1 Two standard test functions

为了有效验证IPSO算法的改进情况，将PSO和IPSO的相关参数取相同值，具体参数设置如下：种群数量n′=30，最大迭代次数为1 000，维数为30，c1=c2=2，ωmax=0.9，ωmin=0.3．分别用上述两种算法对各个测试函数训练30次．图2、3为各函数的图像和适应度变化过程．表2为两种算法最优解的均值和方差．

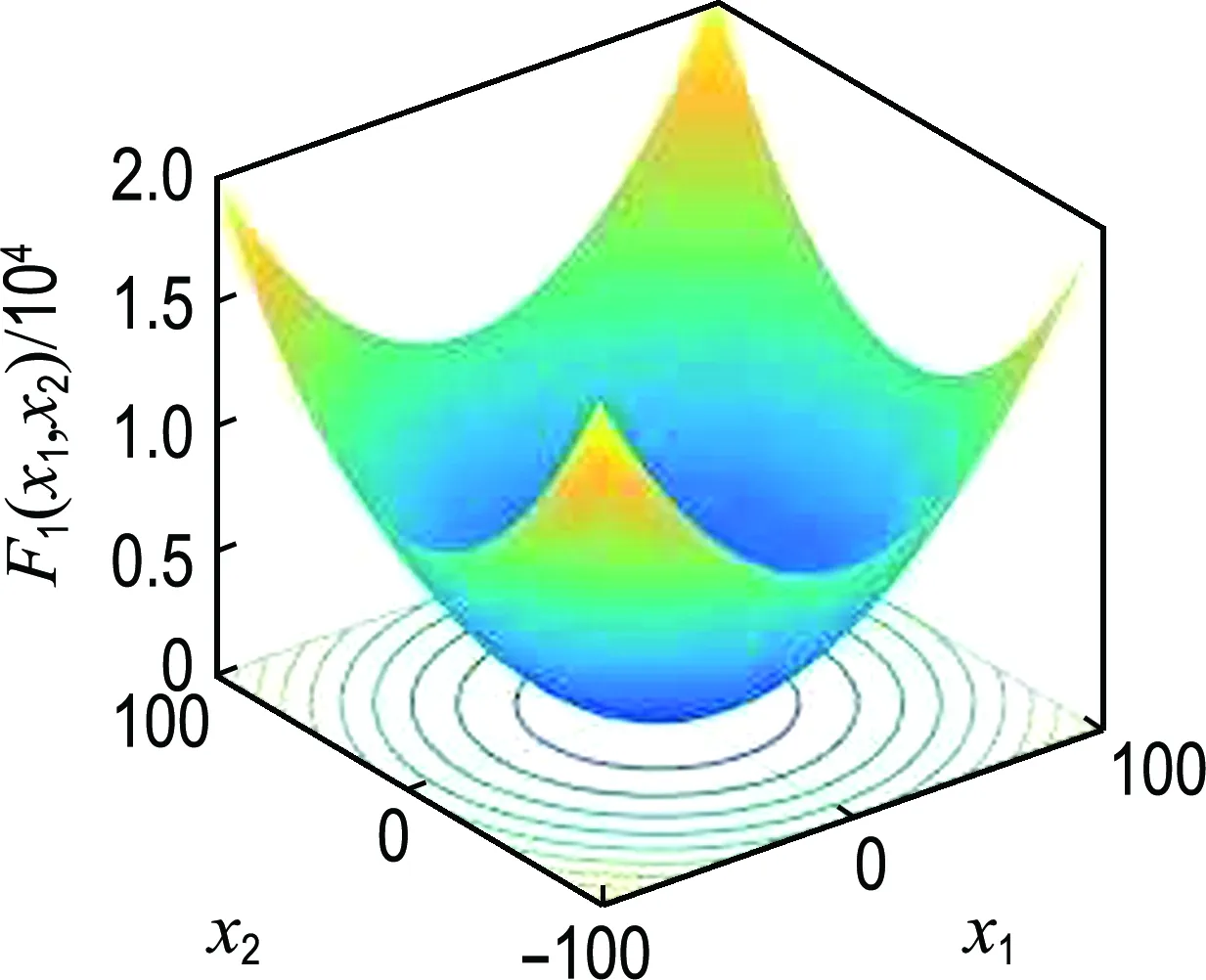
(a)函数图像

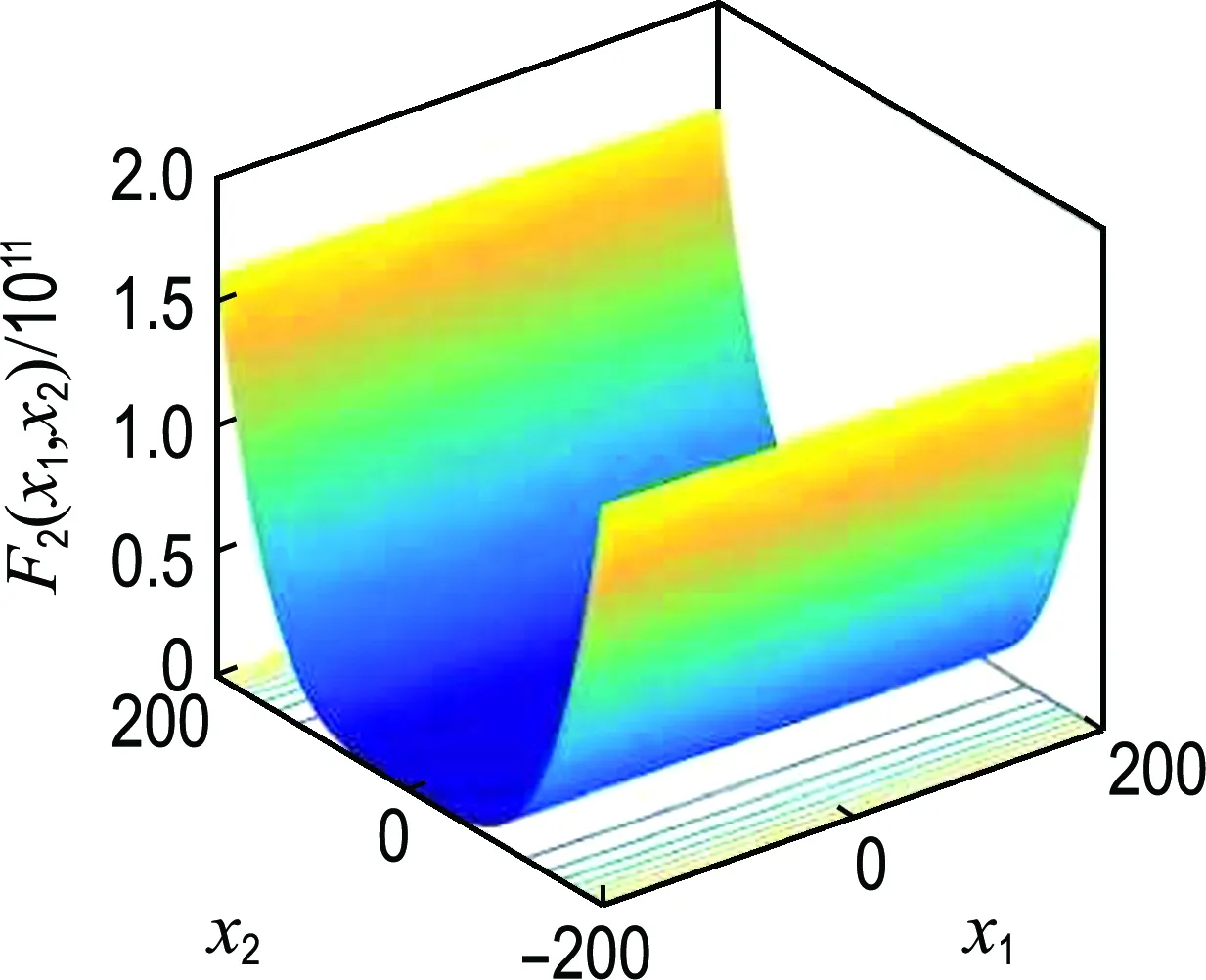
(a)函数图像

从图2、3可以看出，通过IPSO算法计算两种函数最优解的寻优速度明显优于PSO算法．从表2可以看出，IPSO算法最优解均值更接近函数理想解，并且方差也均小于PSO算法．说明改进惯性权重因子的粒子群优化算法相比于惯性权重线性递减的粒子群优化算法无论从精度还是收敛速度方面均表现出了更好的寻优能力．

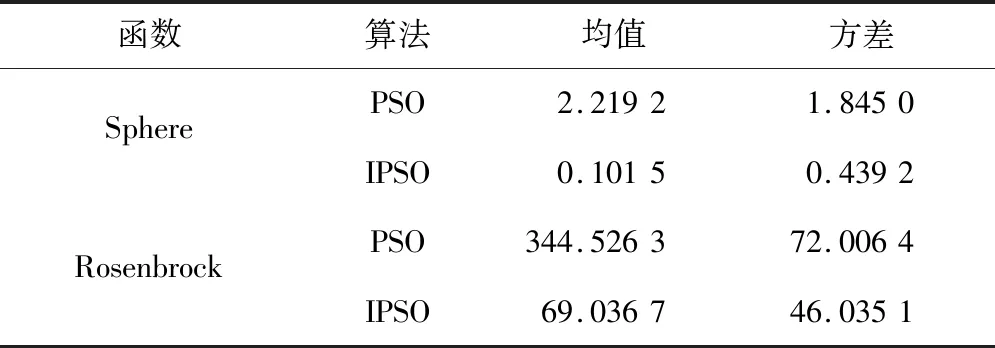
表2 标准函数的计算结果对比Tab.2 Comparison of calculation results of standard functions

2.2 RBF隐含层节点个数的计算

由式(3)可知，在RBF神经网络中隐含层基函数中心、宽度以及隐含层输出权重均为待优化参数，本研究通过PSO算法对上述3个参数进行优化．另一方面，隐含层节点个数对RBF预测结果也有十分重要的影响．研究表明，当隐含层节点太少时，RBF神经网络欠缺学习能力和信息处理能力，无法有效逼近最优结果，导致预测结果与实际偏差过大；反之，当隐含层节点太多时，网络结构将变得复杂和耗时，网络的泛化能力减弱，导致神经网络过度学习，容错能力下降[16]．因此，本研究通过试错法确定隐含层节点个数[17]．

首先根据式(7)得到RBF神经网络隐含层节点个数的初始可行区间[e，f]，通过逐一计算比较区间内的各点，在不断缩小区间的过程中确定最佳的隐含层节点个数．

(7)

式中：nr、nc和ny分别表示RBF神经网络的输入层、输出层和隐含层节点个数．

2.3 IPSO-RBF算法模型

根据上述分析，建立基于IPSO-RBF的沥青路面损坏状况预测模型，具体预测流程如图4所示．

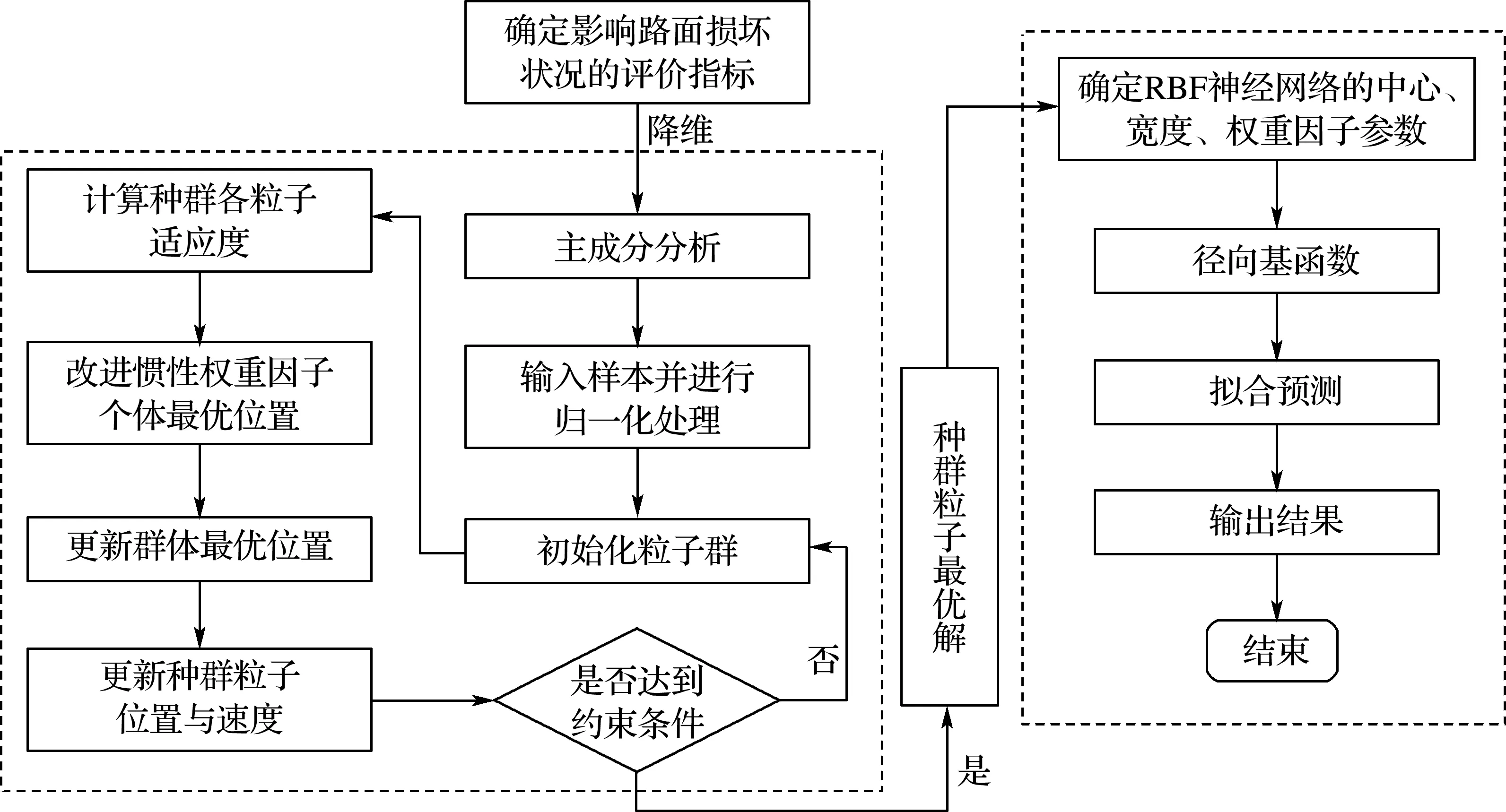
图4 基于IPSO-RBF的沥青路面损坏状况预测流程Fig.4 Prediction process of asphalt pavement damage condition based on IPSO-RBF

具体预测步骤如下：

(1)样本数据归一化．为了去除指标间不同量纲的影响，按照式(8)对样本数据进行归一化处理，使得样本数据介于0、1之间．

(8)

式中：η为样本容量，xi为样本数据，xmin、xmax分别表示样本数据中的最小值、最大值．

(2)筛选路面破损状况主要影响指标．考虑沥青路面损坏状况指数受到多种因素影响，为筛选出主要影响因素，对各影响指标进行灰色关联度分析，通过式(9)计算各影响因素与路面损坏状况指数之间的灰色关联系数，并选取灰色关联系数βij(k)>0.5的各相关指标．

(9)

式中：βij(k)表示x′i(k)与x′j(k)的关联系数；Δmin、Δmax分别表示数据中不同指标间绝对差的最小值与最大值；μ为分辨系数，一般令μ=0.5[18]．

(3)利用主成分分析对主要影响因素进行降维处理，以减少输入层节点个数，实现降维的目的．

(4)确定RBF神经网络结构参数．RBF神经网络的输入层节点个数与主成分个数一致，隐含层节点个数通过式(7)试错法确定．输出层为路面损坏状况指数(Ipc)，节点个数设置为1．

(5)优化RBF神经网络中的3个参数．将RBF神经网络中的参数隐含层中心ci、宽度σi和隐含层输出权重ω以向量(ciσiωi)形式表示粒子群优化算法中的粒子，然后设置IPSO算法中粒子群的种群规模m和最大迭代次数kmax．同时初始化各粒子的飞行速度v和位置x．根据式(6)计算惯性权重因子．

(6)根据式(10)计算粒子适应度．将RBF神经网络的均方误差作为粒子群优化算法的适应度函数计算公式，通过判断粒子当前位置适应度，决定是否更新当前粒子的最优位置和整个粒子群的最优位置．

(10)

式中：y′i表示粒子预测值，yi表示粒子实际值．

(7)根据式(1)、(2)更新粒子的速度和位置．若输出结果满足限制条件或者迭代次数超出限定值，则进行步骤(8)；若输出结果不满足限制条件，则返回步骤(6)，重复迭代过程．

(8)将IPSO模型训练的最终结果作为RBF神经网络的相关参数，建立IPSO-RBF神经网络模型，得到沥青路面破损状况的预测结果．

2.4 预测精度评价

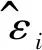
(11)

(12)

(13)

式中：p′i为模型预测值，pi为实际值．

3 实例预测及分析

3.1 原始数据

本研究选取G30连霍高速公路甘肃省内某路段作为研究对象．根据西部地区高海拔的地域特点和寒冷干旱的特殊气候条件，路面性能状况、路面使用状况和路面环境状况对沥青路面破损状况均有一定影响．根据相关公路养护管理部门调查，常见的路面病害主要以车辙、裂缝、龟裂和坑槽为主，占路面全部破损量的89%以上，因此，裂缝率、修补率、龟裂面积率和坑槽率可以在一定程度上反映路面性能状况．路面使用时间的延长、交通量的增加和养护资金不充足，将会对路面破损造成影响，因此，采用路龄、交通量和养护资金作为路面使用状况的评价指标．同时，针对甘肃省日照时间长、降雨量少的特殊气候条件，将降雨量和日照时间作为路面环境评价指标．本研究调查和搜集了该路段近11年来的路面损坏状况指数(Ipc)x1、路龄x2、交通量x3、裂缝率(rc)x4、修补率(rp)x5、龟裂面积率(rm)x6、坑槽率(rt)x7、降雨量x8、日照时间x9和养护资金x10，调查结果如表3所示．

3.2 影响因素关联度分析

运用Matlab 2016a软件对原始数据计算各个影响因素与路面损坏状况指数间的灰色关联度，对表3中Ipc指标与初选的10个相关指标做灰色关联分析，灰色关联度计算结果如表4所示．结果显示，路面损坏状况指数与各影响因素间的灰色关联度排序为x6>x2>x5>x7>x8>x4>x10>x9>x3．本次研究中选取与Ipc关联度大于0.5的7个评价指标作为主要影响因素．

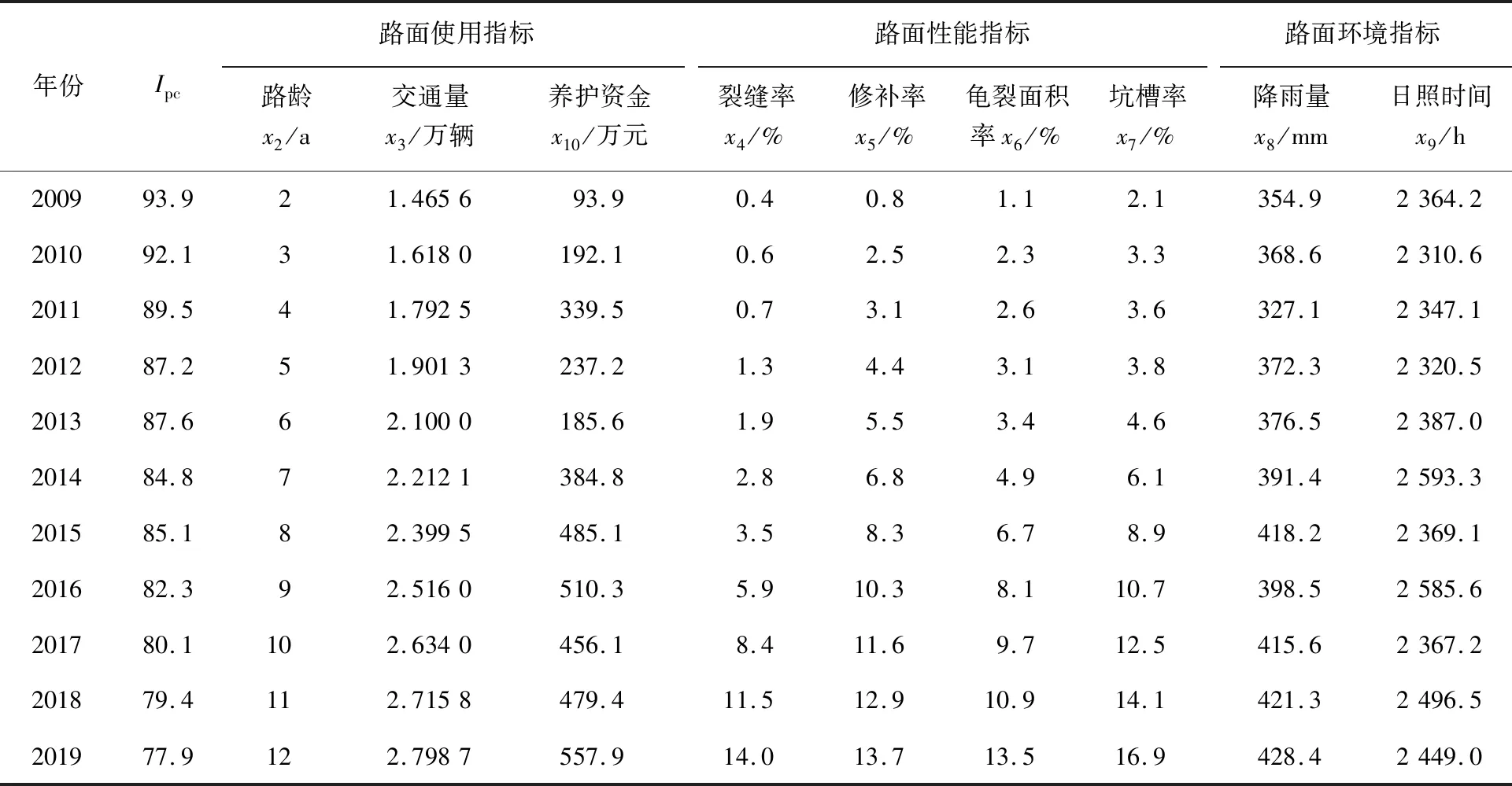
表3 路面损坏状况指数与各影响因素的调查结果Tab.3 Investigation results of road surface pavement condition index and its influencing factors

3.3 主成分分析建模

应用SPSS26软件中的因子分析功能对选取的7个影响因素进行主成分分析．最终选取方差累计贡献率达99.87%的4个主成分，既能够达到降维的目的，又能较为完整地包含影响因素的信息，从而准确反映Ipc与各影响因素之间的关系．根据表4，分别记为p1、p2、p3和p4，则各主成分表达式为

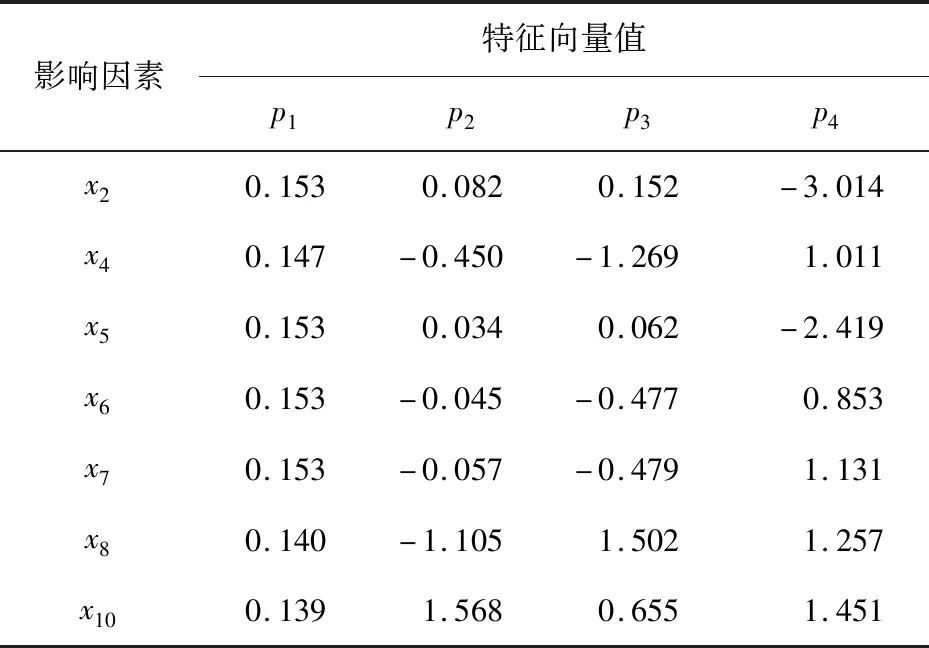
表4 各影响因素的方差贡献率及特征向量Tab.4 Variance contribution rate and corresponding eigenvector of each influencing factor

xIpc=fr1gr1+fr2gr2+…+frngrn

(14)

式中：r为评价要素的个数，frn为各主成分的特征向量值，grn为各主成分的评价要素．

3.4 训练模型

选取2009～2018年归一化后的综合指标数据作为训练样本，2019年的为测试样本．针对本文的研究问题，将IPSO算法具体参数设置如下：粒子种群数n′=100，迭代次数为500，c1=c2=1.7，ωmax=0.9，ωmin=0.4．IPSO-RBF神经网络模型输入层以提取4个主成分值作为输入样本，输入层节点个数为4；以路面损坏状况指数作为输出样本，输出层节点个数为1．经过反复实验可得，当隐含层节点个数为8时，模型预测结果较为精确，逼近效果最优．

3.5 预测结果与分析

IPSO-RBF神经网络模型的均方误差曲线如图5所示，将该模型的预测结果与传统PSO-RBF神经网络和RBF神经网络的预测结果进行比较，如表5所示．

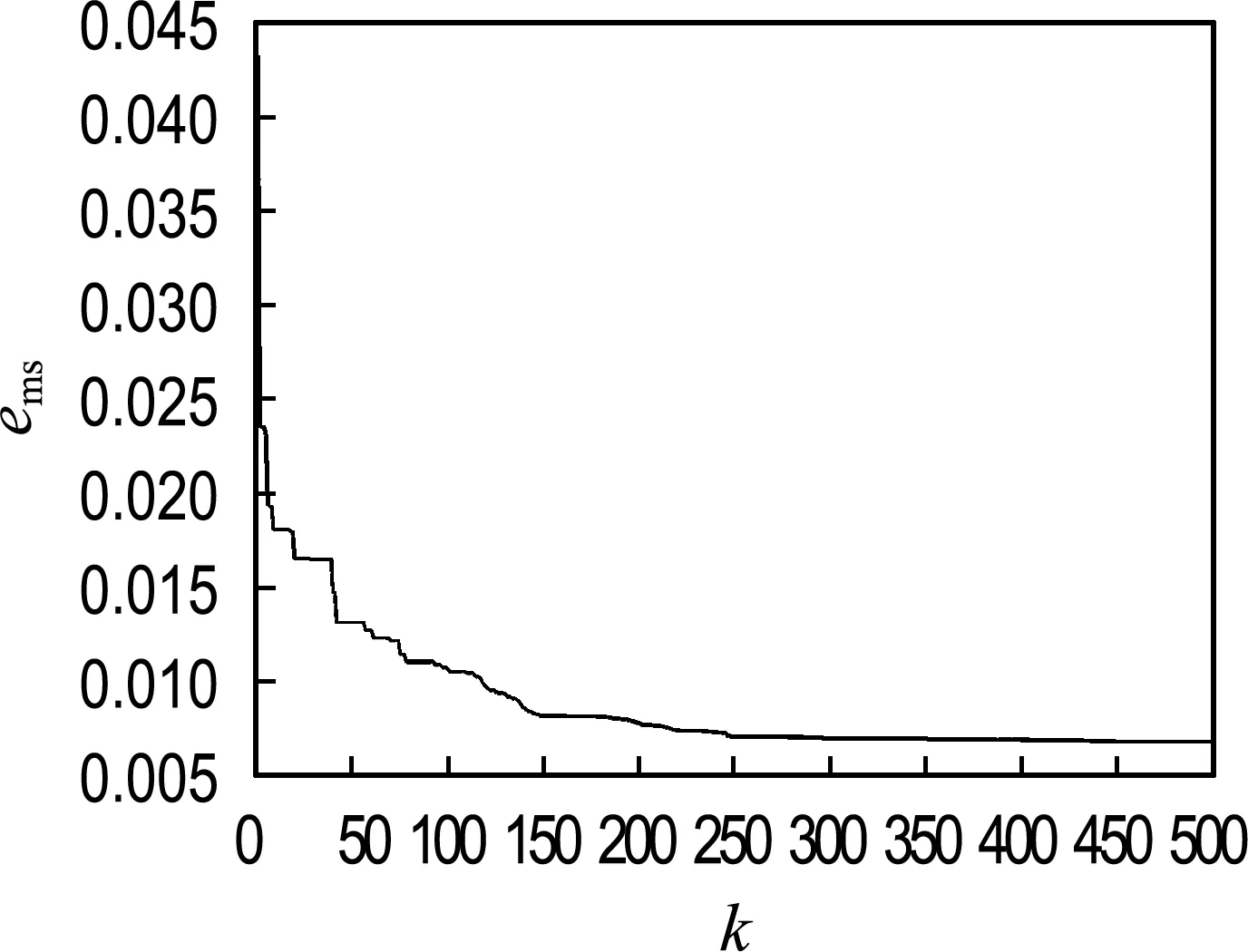
图5 IPSO-RBF预测模型均方误差学习曲线Fig.5 The mean square error learning curve of IPSO-RBF prediction model

综合表5数据可知，IPSO-RBF模型的平均绝对误差为0.841 6，低于PSO-RBF模型的平均绝对误差(1.386 0)，也远低于RBF模型的平均绝对误差(2.271 1)．在相对误差方面，IPSO-RBF模型的相对误差低于2%的有10个，占总样本的90.9%；PSO-RBF模型的相对误差低于2%的有5个，占总样本的45.5%；RBF模型的相对误差低于2%的有4个，占总样本的36.4%．

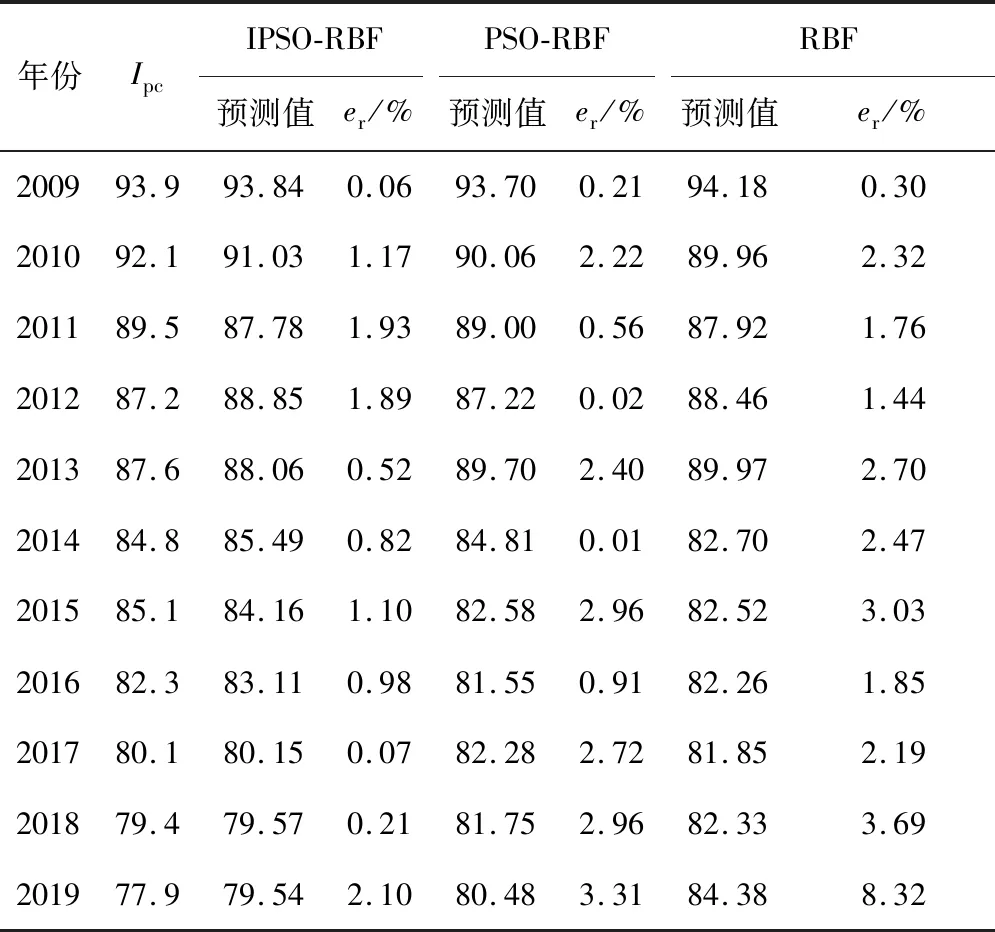
表5 模型预测结果与分析Tab.5 Model prediction results and analysis

图6为3种模型Ipc预测值与实际值变化趋势图．从中可以看出，IPSO-RBF神经网络模型预测曲线与实际值曲线最为接近，且IPSO-RBF神经网络预测模型预测精度波动较小，而PSO-RBF和RBF模型预测精度随着预测时间的增加波动范围变大，因此，IPSO-RBF神经网络预测模型是一种有效的路面破损状况预测方法．

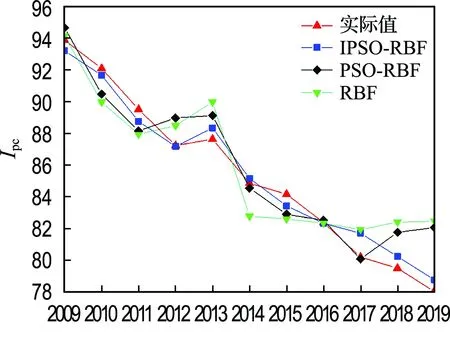
图6 不同模型路面损坏状况指标预测值与实际值变化趋势图Fig.6 Pavement condition index predicted value and actual value change trend chart of different models

4 结 论

(1)利用主成分分析法建立了多维非线性的沥青路面破损状况预测模型．以往学者对路面破损状况预测的研究只针对单一指数，没有充分考虑相关评价指标对路面破损状况的影响．因此，本研究从路面性能、路面使用状况和路面环境状况3个方面，综合考虑路面损坏状况指数、路龄、交通量、裂缝率、修补率、龟裂面积率、坑槽率、降雨量、日照时间和养护资金等对路面损坏状况指数的影响，使路面破损状况的预测模型更加准确．

(2)通过对粒子群优化算法中惯性权重因子进行改进，将IPSO-RBF神经网络预测模型运用在沥青路面破损状况预测中，所得预测结果的平均绝对误差相较PSO-RBF和RBF预测模型分别降低了40.28%和62.94%；预测精度顺序为IPSO-RBF>PSO-RBF>RBF，说明IPSO-RBF神经网络模型是路面破损状况预测的有效方法之一，预测精度更高．

(3)通过实例对优化模型进行验证．IPSO-RBF神经网络模型在沥青路面使用性能预测中获得了较为满意的结果．然而本实例中样本数量不够充足，且路面损坏状况指数变动幅度不是很大，因此，在对个别指标发生较大突变的路段进行路面破损状况预测时，该模型预测结果的精确度还有待进一步探讨．