2021年中考数学文化试题赏析
2022-03-25罗伟
罗 伟
(江苏省徐州市第二十四中学 221000)
南开大学顾沛教授指出,数学文化,从狭义方面说,指数学的思想、精神、方法、观点、语言,以及它们的形成和发展,从广义上说,还包含数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系等.在2021年各地中考中,出现了一些数学文化试题,这些试题能培养学生的方法技能、基本思想、人文素养与科学精神,现从中精选部分试题与读者共赏.
1 基本数学思想
例1
(山西)在勾股定理的学习过程中,我们已经学会了运用如图1和图2的图形验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际 上它也可用于验证数与代数、图形与几何等领域中的许多数学公式和规律,它体现的数学思想是( ).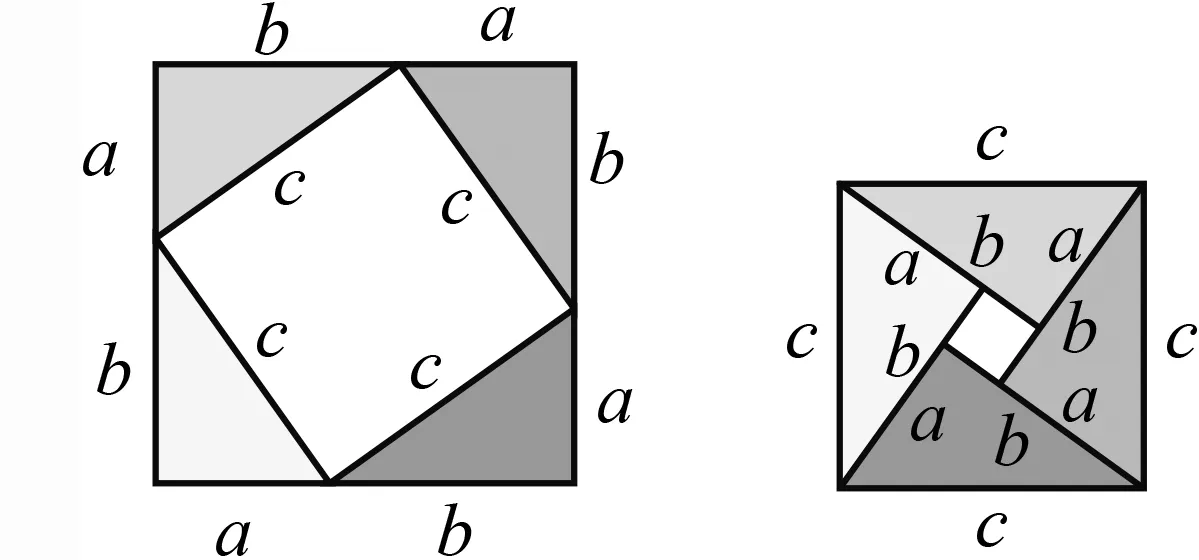
图1 图2
A.统计思想 B.分类思想
C.数形结合思想 D.函数思想
解析 分别弄清两个图中各部分与整体面积之间的关系.
根据图1可得化简得a
+2ab
+b
=2ab
+c
,进而a
+b
=c
.根据图2可得化简得c
= 2ab
+b
-2ab
+a
,进而a
+b
=c
.这两种方法都验证了“直角三角形两直角边的平方和等于斜边的平方”,即勾股定理.因为只有图,省略了解题过程,所以被称为“无字证明”.体现的就是一种数形结合的思想,故选C.赏析
我国著名数学家华罗庚说过:“数缺形时少直观,形少数时难入微.”数形结合是解决数学问题的重要思想方法,而勾股定理被称为“千古第一定理”,是数形结合的典范.我们在平时的教学中也要经常向学生渗透基本数学思想,这是四基之一.去片UCVA≤0.8组验配前具有较高的球镜度(P<0.001)、柱镜度(P<0.001)、较长的可视虹膜直径(P<0.001)和眼轴(P<0.001),2组间年龄、眼压、角膜曲率等参数差异无统计学意义。2组儿童的眼部基本特征数据见表1。
2 中国古代名著
例2
(浙江宁波)我国古代数学名著《张邱建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗.今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清、醑酒各几斗?如果设清酒x
斗,醑酒y
斗,那么可列方程组为( ).
解析 根据题意分别从谷子和酒的斗数找两个相等关系是列二元一次方程组的关键.
设两个未知数之后,要找出两个相等关系:清酒斗数+醑酒斗数=5斗,可得方程x
+y
=5;清酒可换的谷子斗数+醑酒可换的谷子斗数=30斗,可得方程10x
+3y
=30,故选A.赏析
本题考查用二元一次方程组解决中国古算问题.《张邱建算经》系北魏张邱建所著,全书共三卷.现传本保存92个问题,大部分为当时社会生活中的实际问题,如有关测量、纺织、交换、纳税、冶炼、土木工程和利息等.就数学内容而言,包括分数乘除、直角三角形、一次方程(组)、二次方程、等差级数、等比级数和不定方程等,问题的创设和解法均超出《九章算术》,为《九章算术》之后有突出成就的数学著作.据统计,在2021年中考中,考查频数最多的是《九章算术》,有广西、湖北恩施、湖北宜昌、湖南邵阳、江苏宿迁、浙江衢州等地的试卷,这说明它的地位非常高,是中国乃至东方第一部自成体系的数学专著,几乎可以和西方的《几何原本》齐名.其余还有湖北荆门、甘肃白银等地的试卷有题源自《孙子算经》,浙江绍兴卷有题源自《算法统宗》,湖北江汉油田卷有题源自《算学启蒙》等著作.考虑到学生的语文水平,绝大多数先给出文言文,再给出现代汉语翻译.从题的形式看,最多的为用二元一次方程组解决问题的选择题,难度相对较低,另外,还有填空题,涉及列一元一次方程、一元二次方程解决问题,难度略有增大.
3 经典成语故事
例3
(浙江嘉兴)看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上中下三个等级的三匹马记分如表1,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为.
表1
姓名马匹下等马中等马上等马齐王6810田忌579
分析 可通过画树状图或列表把所有可能都排列出来,再求概率.
解
由于田忌的上、中等马分别比齐王的中、下等马强,当齐王的三匹马出场顺序为10,8,6时,田忌的马按5,9,7的顺序出场,田忌才能赢得比赛,当田忌的三匹马随机出场时,双方的对阵情况如表2所示.表2
齐王的马上中下上中下上中下上中下上中下上中下田忌的马上中下上下中中上下中下上下上中下中上
双方的对阵中,只有一种对阵情况田忌能赢,故田忌能赢得比赛的概率为
赏析
“田忌赛马”是中国古代经典的成语故事,是中国历史上有名的揭示如何善用自己的长处去对付对手的短处,从而在竞技中获胜的事例.有时候看似不可能成功的事情,如果换一个角度,换一种方法,或许就会有柳暗花明的效果.就中学阶段来说,这里运用了数学中的统计与概率知识,通常情况下田忌能赢得比赛的概率只有在实际比赛中,田忌打听到齐王的上中下出马顺序,以下上中对决,通过三次对决,田忌三局两胜,从而赢得比赛.到了大学阶段,可看作运筹学知识,基本思想是不强求一局的得失,而争取全盘的胜利,体现了整体思想.在2021年中考中,福建卷也有“田忌赛马”的题目,它的两个问题如下:
(1)如果田忌事先只打探到齐王首局将出“上马”,他首局应出哪种马才可能获得整场比赛的胜利?并求其获胜的概率.
(2)如果田忌事先无法打探到齐王各局的出马情况,他是否必败无疑?若是,请说明理由;若不是,请列出田忌获得整场比赛胜利的所有对阵情况,并求其获胜的概率.
福建卷考查的情形更细致,更能看出概率在实际生活中的价值及重要性.中国的成语故事很多,有的确实可以构造数学情境,增加数学韵味,如2020年中考中的新“龟兔赛跑”.将一些引人入胜的成语故事编成令人称奇的数学趣题,这也是下一步教师和学生的新目标.
4 趣味数学拼图
例4
(四川乐山)七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板(图3).19世纪七巧板传到国外,被称为“唐图”(意为“来自中国的拼图”),图4是由边长为4的正方形分割制作的七巧板拼摆成的“叶问蹬”图,则图中抬起的“腿”(即阴影部分)的面积为( ).
图3 图4
解析 找出阴影中直角三角形与平行四边形的边与大正方形的边的关系是关键,再求出面积.
由边长为4的正方形分割制作的七巧板,共有五种不同的图形(图5~9).其中图5~7均为等腰直角三角形,腰长分别为图8为正方形,边长为图9为平行四边形,边长分别是2和两角分别是45°和135°.根据图4可知,图中抬起的“腿”是图7和图9拼接而成,腰长是的等腰直角三角形的面积是根据平行四边形的性质可知,两角分别是45°和135°的平行四边形ABCD
(图10)的高是DB
,且平行四边形的面积为因此“腿”的面积为1+2=3,故选A.
图5 图6 图7

图8 图9 图10
赏析
本题考查了七巧板中的图形的构成和面积计算,熟悉七巧板中图形的分类是解题的关键.七巧板可拼成一千多种图形,充分显示了我国古代劳动人民的智慧,“叶问蹬”图就非常形象生动.在2021年中考中,还有江西卷考查了七巧板拼成轴对称图形,浙江金华卷考查了七巧板拼图后相关顶点的坐标,浙江丽水卷考查了七巧板拼图后两平行线的距离等,这些问题的本质是弄清五个基本图形的边、角、面积、周长等数量关系.5 著名文化遗产
例5
(浙江宁波)抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图11,AC
,BD
分别与⊙O
相切于点C
,D
,延长AC
,BD
交于点P
.若∠P
=120°,⊙O
的半径为6 cm,则图中的长为cm.(结果保留π)

图11
解析的半径是已知条件,关键是求出所对的圆心角,所以要先作辅助线.
连结OC
,OD
(图12),因为点C
,D
均是切点,所以OC
⊥AC
,OD
⊥BD
,故∠OCP
=∠ODP
=90°.根据四边形内角和等于360°可得,∠O
=360°-∠OCP
-∠ODP
-∠P
=360°-90°-90°-120°=60°,所以的长为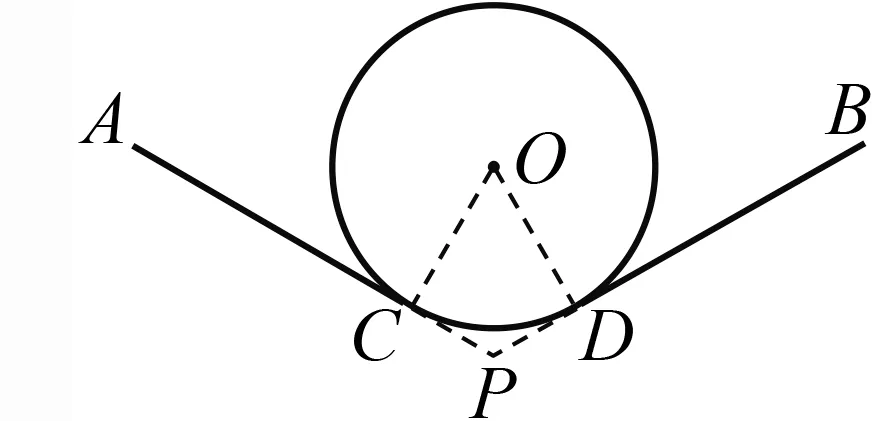
图12
赏析
本题通过作辅助线,先求弧对应的圆心角的度数,再根据弧长公式求解.对于抖空竹这一富有技巧性的健身运动,很多学生都见过.实际上,这里面也蕴含着直线与圆相切的数学知识,丰富了我们的思维.文化遗产是我们宝贵的财富,在2021年中考中,有关我们熟悉的非物质文化遗产太极拳,湖南张家界卷考查了太极图的面积问题,河南卷则考查了世界文化遗产龙门石窟与三角函数的计算,彰显了传统文化中的数学魅力以及数学的应用价值.
6 国际数学视野
例6
(浙江温州)图13是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图14所示的四边形OABC
.若AB
=BC
=1,∠AOB
=α
,则OC
的值为( ).
图13 图14
解析 要先运用三角函数将OB
表示出来,再运用勾股定理即可求得结果.因为AB
=BC
=1,在Rt△OAB
中,故在Rt△OBC
中,根据勾股定理得故选A.赏析
本题主要运用三角函数与勾股定理求解.我们可以看出第七届国际数学教育大会的会徽非常漂亮,一个三角形不断向外“扩张”,形如“迭代”的效果.在2021年中考中,还有甘肃武威卷根据古希腊数学家阿基米德提出的有关圆的一个引理,让学生作图,湖北宜昌卷考查了“莱洛三角形”的面积计算问题,四川成都卷考查了菲尔兹奖获得者年龄的统计问题等,数学无国界,这些题目让我们开阔了视野,增长了见识.
中考试卷中数学文化试题不断涌现,显示了命题者的聪明与智慧,这也是学科育人的一种途径.学生在做题过程中巩固了知识与技能,培养了思维能力,感受传统文化的熏陶.在日常教学中,教师可以精选蕴含传统数学文化的问题让学生阅读、欣赏和解答,品味数学文化的精髓,引导学生发现这类问题所需要的知识、思想和方法.另外,教师可以推荐学生课余时间阅读《九章算术》《孙子算经》《几何原本》等名著,写些心得体会,体会数学文化之美,领略中外数学精神,进而提升自己的数学文化素养,力争做到“文化搭台,学生唱戏,教师喝彩”!
