折角、画角与作角:渐次展开并平滑“转场”
——苏科版七上“角(2)”教学设计与解读
2022-03-25许小燕
许小燕
(江苏省泰州市姜堰区实验初级中学 225599)
最近在线收看了某地教研直播活动,一位青年教师执教苏科版七上“角(2)”,教师的教学基本功很好,教学预设了一些数学实验和情境活动,教学过程中师生有较多互动,课堂氛围比较热烈.然而由于该教师是“严格”根据教材内容的顺序开展教学,使得前后教学环节之间的过渡不够“平滑”.笔者认真研读了该课时的教材内容后进行了再设计,并给出教学立意的阐释,抛砖引玉,供研讨.
1 “角(2)”教学设计概述
教学活动1
透明纸“折角”引入情境 出示一张画有∠AOB
(图1)的透明纸,让学生回顾角的定义,接着从角的定义出发,安排学生用符号表示这个角,然后将透明纸上的这个角对折,使角的两边重合,再展开透明纸,折痕把这个角分成两个相等的角(图2).
图1 图2
如图2,把透明纸上的折痕记为射线OC
,射线OC
把∠AOB
分成两个相等的角,射线OC
叫做这个角的角平分线.追问 图2中共有几个角?它们有怎样的数量关系?(预设:学生能说出很多,教师梳理成角平分线的符号语言,板书如下)
因为OC
是∠AOB
的角平分线,所以或∠AOB
=2∠AOC
=2∠BOC
.变式练习1 如图3,OD
平分∠BOC
,∠AOC
=2∠BOD
,图中OC
是∠AOB
的角平分线吗?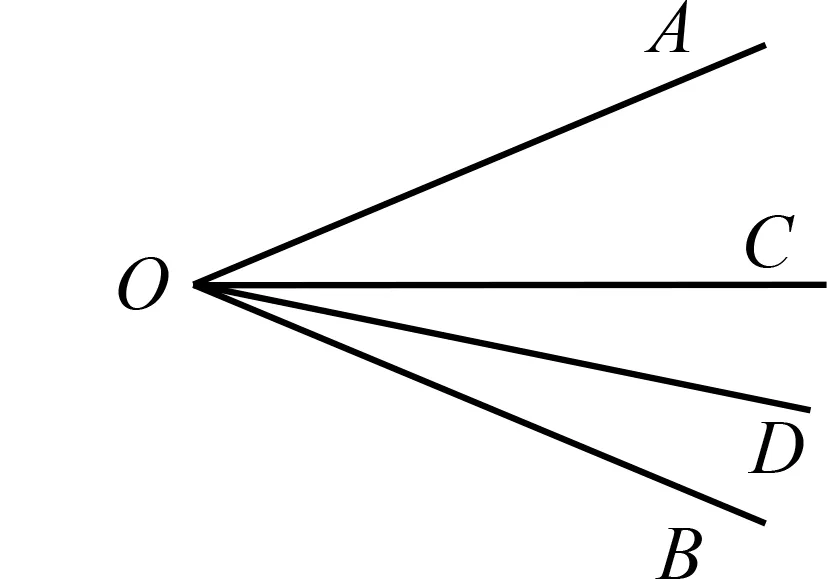
图3
设计意图
反馈学生对角平分线定义是否理解,以及能否初步运用符号语言说明理由.变式练习2 如图4,打台球时,球的反射角等于入射角.中间的“虚射线”(不妨称它为“基准线”或“法线”)可看成是图5中∠AOB
的角平分线.怎样画出OA
,OB
之间的“基准线”?
图4 图5
设计意图
这是一种不同的设问方式,要求学生画出“基准线”,本质上就是追问学生这种设问的等价问题“画出∠AOB
的平分线”.学生可能会继续使用“折角”的方法,但这里不再是透明纸,可能画在一个作业本上不方便折叠,这就引出量角器这种度量工具.学生可以先使用量角器度量出∠AOB
的度数,然后算出它的一半,进而再用量角器以OA
为一边,在∠AOB
内部画出一条射线OC
,使∠AOC
等于∠AOB
的一半,则射线OC
就是符合要求的“基准线”(即OC
是∠AOB
的角平分线).通过以上分析,可以看出吴钧陶在翻译文化负载词时,充分把“归化”和“异化”两种翻译方法结合。通过他的译本,也对音译、音译加注释、直译、直译加注释、和意译加注释翻译文化负载词的一些方法有了深入的了解。虽然部分词语的翻译对儿童读者产生了一定的阅读困难,但是由于保留了源语言的文化色彩,也能够使读者更多地了解接触异国文化。因此,译者应当从目标读者的角度出发,在实践的基础上不断探索,以寻求更好的文化负载词的译法。
教学活动2
量角器“画角”过渡 “由上面使用量角器画出角平分线的画法可以知道同学们已学会了使用量角器画一个角的方法.其实,当我们量出图5中∠AOB
等于60°,算出它的一半是30°时,还可借助常用的三角板来画图,一个含30°角的三角板可以帮助我们直接画出30°角.同学们想想,借助一副三角板还可以画出哪些角度?可以先在小组内交流.”教学组织 待学生小组内交流之后,安排学生使用一副三角板到讲台前演示.如果说得不全,可以安排其他同学上台继续演示、补充,直到最后总结出一副三角板可以画出15°角的任意倍数的角.
练习 先画一个角∠AOB
=30°,在此图形的基础上,再画一个角∠AOD
=80°.教学组织 学生画30°角时可能使用量角器或三角板,再画80°角时就只能使用量角器了,但是这个画图需要分两种情形画出射线OD
的可能位置(图6,图7),教学时可展示不同的图形,培养学生严谨的解题习惯.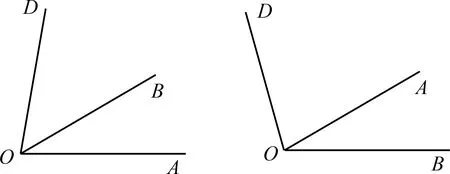
图6 图7
追问 以图6为例,在∠BOD
内部,再画一条射线OC
(如图8),使OB
是∠AOC
的平分线.同学们能求图8中哪些角的角度?
图8
设计意图
这个“追问”对应着苏科版七上第156页的例题.过渡 “同学们已学会了使用一副三角板、量角器画角的方法,现在我们来类比前面尺规作线段的方法,如果仅允许使用没有刻度的直尺和圆规来作角,从‘画角’到‘作角’,一字之差,充满了挑战.那么同学们思考一下,如何用尺规作一个角等于已知角?”(给学生几分钟时间独立探究后再分小组交流,教师巡视各小组的进展,如果在小组内探究出来就安排他们派代表上台演示、讲解,但笔者执教该课时,基本上没有学生能在5分钟之内独立探究出作法.)
教学组织 教师在学生独立探究5分钟左右仍然得不出作法后,可以进行示范式讲解,并使用PPT渐次呈现相应的操作步骤(几何语言).提醒学生在一张透明纸上作图(便于稍后利用透明纸对所作出的角进行叠合、验证),学生边听讲解边模仿作图.值得提醒的是,如果教师“一气呵成”作出一个角等于已知角(图9,图10)后再动手,至少有一大半的学生无法辨别其中一些步骤的先后顺序,导致作图出错或无从下手.等学生作图成功后,安排他们将作出来的角(透明纸上的图10)与图9中的角进行叠合验证,确认它们能完全重合后,说明这种尺规作角的方法是可行的.

图9 图10
练习 再来看“打台球”问题,在图11中黑色球能否被击入右下角的袋中?先估测,再用直尺和圆规作出反射角加以检验.

图11
教学组织 这是安排尺规作角的巩固训练,由于图形位置与情境的干扰,有些学生可能会出现困难,这时可以让作图顺利的学生上台展示、讲解,分享他们成功的经验.
教学活动4
课堂小结,练习巩固结合板书(图12),提了两个小结问题.

图12
小结问题1 本课从角的定义出发,利用透明纸折出一个角的平分线,结合图形说说你对角平分线的理解;
小结问题2 从“画图”到“作图”,你是如何辨别这里“画”和“作”的一字之差的?
布置作业 课本上第157页第6,7,8题.
2 教学立意的进一步解读
2.1 分析教材内容,重组教学顺序
由于本课时学习内容是角的第2课时,教材内容主要是从画图到作图,再利用透明纸折出角平分线,然后进行角平分线相关例习题训练.教学目标是掌握角平分线、量角器画角,学会用直尺和圆规作一个角等于已知角.教学重点是角平分线的符号语言及初步解题运用,教学难点是尺规作角,特别是如何向学生“说清道明”尺规作图的理由(我们采用的方法是让学生将尺规作出的角画在透明纸上,然后小组内进行叠合验证,本质上是验证了三角形全等的条件“边边边”).基于由易到难、渐次展开的设想,我们重组教材内容的呈现顺序,本课的教学流程依次是“折角”“画角”“作角”,在每个教学活动下面跟进一些练习或变式(或追问),力求不同教学环节之间能平滑“转场”(转场更多的是用在影视、戏剧艺术中,在两个场景之间采用一定的技巧,实现场景或情节之间的平滑过渡,或达到丰富画面吸引观众的效果).
2.2 明辨新知特点,启发示范并行
通过恰当的情境创设促进学生能独立探究、归纳出数学新知或性质,是我们共同的教学追求.然而,几何起始阶段,有些几何新知(定义、符号语言或作图方法)在短时间内不易掌握,为了平衡自主探究的教学时间成本,还是应该有(或预设)必要的示范讲授.比如,本课教学内容中角平分线的定义及符号语言是需要教师讲授的,另外尺规作角的步骤也需要教师示范讲授,这些内容难以让学生独立探究出来(或者说更准确、简练地表达出来).而使用三角尺、量角器画图则是学生在小学阶段就有所接触且可以顺利完成的,教师只要稍加引导、启发即可.在一些画图或作图之后安排了练习或变式练习,也需要让学生先经过独立思考、解题,再安排小组内交流讨论,最后再进行全班展示、分享或纠错(比如漏解).笔者以为,一般来说,对于数学对象的定义,经过简短的情境铺垫、归纳概括之后,教师可以直接给出教材上定义的内容并板书,然后组织学生理解教材为什么这样定义,包括对定义中有些限制条件、范围表述的辨析;此外对于短时间内很难想到的思路(比如证明勾股定理时的拼图或构图,本质上是奇妙的辅助线添加),也可直接给出或向学生推介这种思路,然后带领学生理解思路或证明方法,这也是弗赖登塔尔所提出的“有指导的再创造”.
2.3 基于变式教学,加强前后关联
本课教学设计充分体现了变式教学的运用.具体来说,比如角平分线的定义,透明纸折出角平分线,到定义的文字表述和符号语言,体现了角平分线定义的变式呈现、多元表征,有利于学生从不同角度理解和掌握.再比如,本课中的练习题的选编都是以变式题组的方式呈现,而且不同环节的习题背景还做到前后关联,“打台球”的问题情境在两个教学环节中都得到体现.还有,透明纸在开课引出角平分线时使用过,在后来尺规作角时又让学生使用,以验证作出的角是否能完全重合,这体现了透明纸在前后不同环节中的关联呼应.
