基于MATLAB在砂芯夹持器系统中的稳定性分析

林显新 叶城保

摘 要：发动机铸件生产过程中，砂芯模型采用工业机器人转配，受机械振动，夹持压力，加减速等外部干扰因素导致砂芯出现裂痕，影响后续铸铁质量，本文通过构建夹持器系统的数学模型，通过串联夹持压力测量环节，形成闭环反馈系统，进而分析系统的输出响应，最终获得较优控制系统。

关键词：MATLAB 夹持器 稳定性 工业机器人

1 引言

随着智能制造产业的转型升级，“机器换人”已成为未来发展主攻方向。发动机生产车间铸造工段的废气、粉尘、噪声和振动严重影响着现场生产人员的身心健康，采用工业机器人进行物料搬运、组装有利于提高生产效率[1]。由于发动机铸铁采用砂芯模型进行铁水浇铸，砂芯模型的质量对发动机质量起着至关重要的作用。砂芯采用树脂与三乙胺凝固而成，硬度不高，使用工业机器人进行搬运、装配等会出现夹不稳或者夹裂等问题。本文以工业机器人夹持器系统为研究对象，分析其输出响应的稳定性。

2 夹持系统现状分析

2.1 搭建夹持系统的数学模型

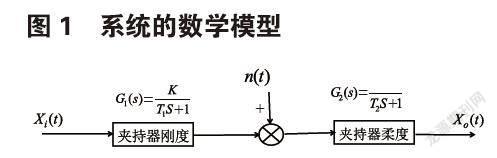
装配砂芯的工业机器人夹持系统采用柔度与硬度对半的夹持器，夹持器背面采用铝合金板保证夹持的刚度，夹持器接触面采用软性较好的橡胶，保证砂芯的夹持柔度。系统受夹持压力、机械振动和加减速运动等因素干扰。根据系统各环节因素，构建夹持器系统，如图1所示。

计算刚度环节系数K受结构压力与形变相关（K=P/），砂型重量约为6Kg，夹持面形变约0.5mm，即K为120N/mm，柔度环节λ受夹持器长度、接触面和压杆系数影响（λ=μl/i），其中μ为压杆长度系数0.7，l为夹持器长度12cm，i为接触面长度1.5cm，因此λ=5.6，当外界干扰信号为单位脉冲函数N（t）=δ（t）时，对函数Laplace反变换得N（s）=1[1]。

夹持器中刚度环节传递函数为G1（s）。

式（1）中，T1为惯性环节的时间常数（T1≥0）。

夹持器柔度环节的传递函数为G2（s）。

式（2）中，T2为惯性环节的时间常数T2≥0。

式（1）、（2）作为一阶惯性环节，当T1=T2=1s时，系统前向通道的开环传递函数为Gk（s）=G1*G2，求出Gk（s）。

2.2 开环夹持系统的响应

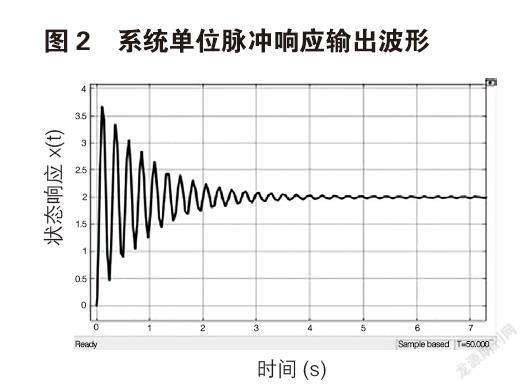
若系统输入信号与干扰信号均为单位脉冲时，将Gk（s）通过Matlab/Simulink对系统模型进行仿真分析，系统在干扰冲击作用下，系统响应输出波形如图2所示。

由仿真结果可知，系统在受到外界干扰的情况下，出现振荡，超调量为σ=85%，系统受外界干扰冲击影响较大，而正是由于系统振荡导致镂空砂芯受力不均匀而出现裂痕，给后面铸铁浇铸带来很大的废品率。因此需要通过增加夹持器压力检测反馈环节，减少干扰导致的振荡，降低系统超调量σ。

3 系统优化控制

3.1 增加压力测量反馈环节

在原来夹持系统的基础上，增加气压测量反馈环节，形成闭环控制，如图3所示。

假设外界干扰因素为单位脉冲函数N（t）=δ（t）时，对应函数Laplace反变换得N（s）=1，测量反馈环节为单位负反馈，H（s）=1，则闭环系统的传递函数为GB（s）。

3.2 闭环夹持系统的响应

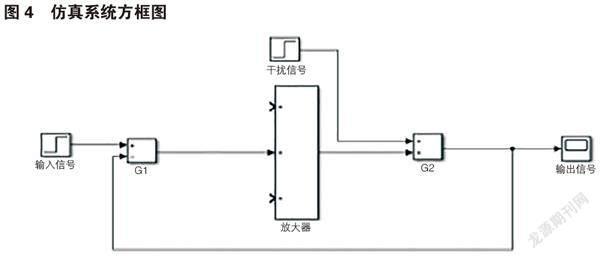
根据铸造中心工业机器人夹持器的工作原理、机械结构，考虑机械振动等干扰冲击因素，在夹持器末端串联一个气压检测环节，将检测信号反馈给工业机器人控制系统。在Matlab/Simulink中搭建一个闭环负反馈控制系统的数学模型[2-3]，如图4所示。

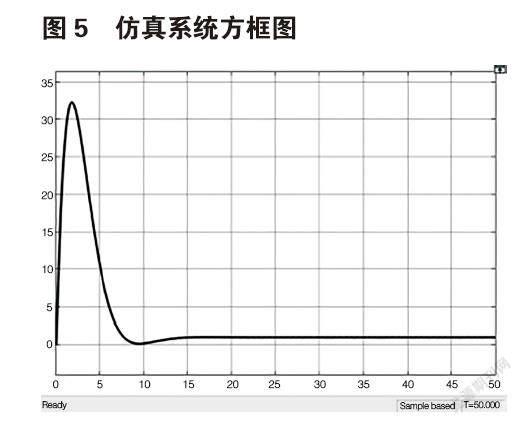
运行仿真，运行完毕后，双击示波器“Scope”，查看系统的响应输出，得到如图5所示的波形。

由仿真结果可知，系统只经历过一次振荡就趋于稳定，且输出较为平缓，输出响应明显好于开环系统。

4 结论

通过增加夹持系统的气压测量反馈环节，在夹持器执行末端串联一个电子气压表，用于检测夹持气压，当气压达到设定气压值时，输出一个脉冲信号给机器人，机器人通过实时检测该气压信号，用于控制氣路的接通与断开，进而较好的控制夹持器夹紧压力，保证砂芯的不被夹裂或者夹不稳等现象出现，进而保证了后续铸铁的质量，为制芯段采用工业机器人装配起到一定参考作用。

基金项目：2021年度广西高校中青年教师科研基础能力提升项目（2021KY1080）：“铸造中心装配机器人柔性夹持器的研究与应用”。

参考文献：

[1]林显新，李国进，周世凯.基于Matlab的制芯机器人夹持器稳定性研究与分析[J].制造技术与机床，2020，（03）：109-113.

[2]董言敏.工业机器人在智能制造中的应用分析[J].时代汽车，2021，No.363（15）：14-15.

[3]于亚平.智能制造与机器人应用关键技术研究[J].时代汽车，2020，No.340（16）：8-9.

[4]林显新，林德智，李玺. 关于铸造制芯段工业机器人稳定性的探讨[J]. 中国机械，2021（14）.

[5]侯晓楠，杨尊熙.谈工业机器人在汽车制造领域的应用[J].时代汽车，2018，No.293（02）：69-70.

[6]林显新. 铸造制芯段工业机器人夹具的应用设计[J]. 轻工科技，2017（2）.

[7]李小伟.基于MATLAB的工业机器人运动学分析与仿真[J].内燃机与配件，2022（02）：233-237.