颗粒形状在稳定堆积中的等效滚动阻力参数研究

孙卉竹，高政国，王 丹

(1.中国矿业大学(北京)力学与建筑工程学院，北京 100083；2.北京航空航天大学 交通科学与工程学院，北京 100191)

颗粒材料在日常生活、工业工程及土木工程应用中十分常见，其力学行为在各工程领域备受关注。颗粒介质材料的宏观力学性质与颗粒的细观结构特征有着紧密的联系，颗粒间的接触特性、颗粒的形状和尺寸等都对颗粒介质的力学特性产生显著影响，如工业过程中颗粒原料的存储及管道输运性能，土木工程中的边坡稳定及泥石流灾害等。

大量研究表明，颗粒堆积休止角随滑动摩擦系数的增大而增大[1-4]。王家全等[5]采用离散元方法模拟颗粒堆积试验发现当滑动摩擦系数小于0.5时，休止角随摩擦系数的增大而增大；当摩擦系数大于0.5时，休止角的大小基本不受摩擦系数的影响。然而颗粒堆积体的休止角不仅受颗粒间的接触特性的影响，还与颗粒自身的形状、粒径等性质有关。刘军等[6]利用自开发的离散元程序模拟了二维砂堆的形成过程，发现休止角随颗粒尺寸的减小而减小并逐渐趋于某一常值。但Li等[7]通过颗粒桩数值试验发现颗粒尺寸越大，休止角越小。张成功等[8]通过模拟分析粒状材料圆柱试样的塌落破坏机制，发现不规则形状的颗粒试样可降低颗粒角速度，并可得到较大的最后塌落高度和跑出距离。陈国强等[9]用玉米颗粒进行了颗粒堆积离散元模拟，发现在颗粒干燥条件下，楔形颗粒的堆积角与3D扫描的真实颗粒的堆积角相近。

Oda等[10]通过数值模拟和试验研究，发现颗粒形状对颗粒介质的强度有一定控制作用。刘源等[11]也通过试验得到类似结论。随后一些学者[4，12-13]通过大量模拟试验进一步发现，颗粒形状越不规则，材料的抗剪强度越高。然而龚健等[14]在模拟直剪试验中发现，峰值强度与残余强度受颗粒的球形度的影响很小。王蕴嘉等[15]通过等向固结和常规三轴试验，发现当颗粒球度比较高且级配均匀时，球度主要会影响试样残余摩擦角的大小，而对于峰值摩擦角的影响不明显，同时颗粒的形状也主要通过影响试样内部的接触和接触力的各向异性程度来影响试样的宏观表现。Al-Hussaini[16]经由试验研究发现，碎石颗粒的内摩擦角会随颗粒平均粒径的增加而增加。Han等[17]通过对10种不同粒径的砂粒进行界面直剪试验发现，当沿同一界面剪切时，颗粒粒径越小界面摩擦角越大。李存柱等[18]在研究粗粒料宏观力学性质时发现，颗粒的形状系数与材料内摩擦角近似呈线性负相关，同时材料的峰值强度和残余强度均随颗粒形状系数的增加而减小。戴北冰等[19]采用玻璃珠进行室内直剪试验，发现颗粒材料的剪胀性随颗粒粒径的增大而增强。任树林等[20]在研究断层破碎带颗粒形状对断层摩擦强度的影响时发现，异形颗粒的咬合自锁作用提高了其填充的断层破碎带摩擦强度。康馨等[21]则揭示了颗粒形状影响临界状态摩擦角的主要原因。邹宇雄等[22]通过模拟椭球形颗粒以及具有抗转动能力的圆球颗粒的三轴剪切试验，发现颗粒形状对峰值内摩擦角和剪胀性的影响呈现明显收敛性。王怡舒等[23]在研究颗粒接触摩擦对颗粒体宏细观力学特性和能量演变的影响规律时，发现了滚动摩擦系数对宏观应力应变影响规律在不同滑动摩擦系数下的差异性。

由此可见，在现有的研究中，不同研究者对于颗粒介质力学特性的研究结果并不一致，而且研究内容主要集中在颗粒自身性质和粒间接触特性对颗粒材料强度的影响，关于颗粒形状和粒间摩擦力对颗粒材料宏观构型稳定性作用机理以及二者之间关系的研究尚有不足，需要进一步研究。

为研究颗粒形状对颗粒材料堆积稳定性的影响，选用亚克力有机材料建立颗粒数值模型。亚克力颗粒是工业生产中常见的一种生产原料，颗粒的宏观力学行为影响着生产的加工工艺及过程。为此选用亚克力材料物理力学参数建立数值模型，通过有限元模型多边形颗粒和离散元模型考虑滚动摩擦阻力的圆形颗粒的堆积过程模拟，研究了颗粒形状与颗粒间摩擦特性对颗粒堆积稳定性的影响。建立了4种多边形颗粒形状变化的等效滚动摩擦系数表征，为颗粒材料堆积稳定特性的离散元算法研究提供依据。

1 多边形颗粒堆积过程有限元模拟

1.1 多边形颗粒的生成及模型的构建

为研究颗粒形状对颗粒体系稳定性的影响，采用二维颗粒模型，选取正三角形、正五边形、正六边形和正八边形四种形状的颗粒进行堆积过程的模拟，为有效表征颗粒不规则形状与滚动摩擦阻力之间的关系，引入形状系数s[24]：

(1)

式中：A为正多边形颗粒的面积，P为正多边形颗粒的周长。由式(1)可知，形状系数s越大，颗粒形状越接近于圆形，当形状系数s等于1时，颗粒为圆形。控制四种形状颗粒的面积完全相同，生成的颗粒示意图如图1所示。

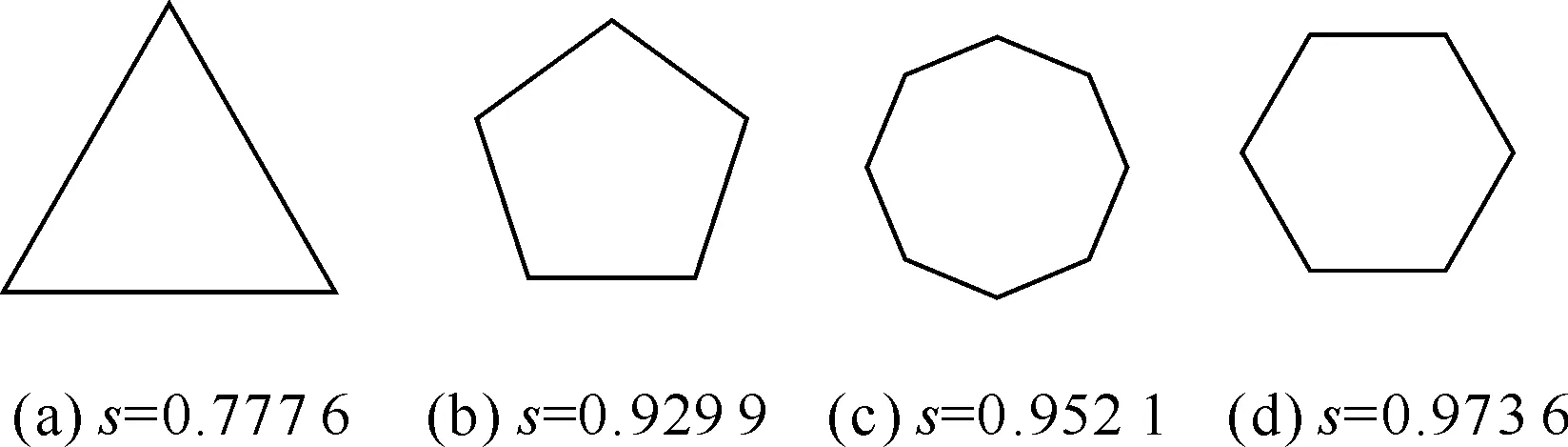
图1 多边形颗粒示意图

多边形颗粒在重力作用下形成自然堆积体，在此过程中可以通过测量分析堆积体的堆积角、堆积高度或堆积层数等宏观数据来研究颗粒形状不规则程度和颗粒间接触特性在颗粒材料堆积过程中的影响。建立的颗粒堆积有限元模型如图2所示(以正五边形颗粒为例)，该模型由两条固定长边界和两条可移动短边界组成，颗粒数量为81，将81个颗粒投放于四条边界所围成的正方形区域内进行堆积过程的模拟。为避免边界与颗粒间的摩擦作用影响模拟结果，设置边界与颗粒之间的滑动摩擦系数和颗粒与颗粒之间的滑动摩擦系数相同。

图2 多边形颗粒堆积有限元模型

1.2 有限元模拟过程

多边形颗粒堆积过程模拟的初始条件为限制模型z方向上的所有位移，水平短边界可以在x方向上运动，多边形颗粒可以在x、y两个方向上运动，对颗粒施加重力荷载。堆积过程分为两个阶段：

(1)颗粒投放下落过程。将多边形颗粒投放到四条边界围成的正方形区域内，颗粒在重力作用下自由下落并达到初始稳定状态。

(2)颗粒运动堆积过程。左右两侧短边界以一定速度匀速向两边移动，颗粒随边界向两边扩散直至与边界失去接触并达到最终稳定状态。

堆积过程如图3所示。

图3 多边形颗粒堆积过程示意图

计算时，颗粒材料的密度ρ为1 200 kg/m3，泊松比ν为0.2，弹性模量E为2×109Pa，与常晓林等[13]、龚健等[14]、康馨等[21]和杜欣等[25]的取值在同一数量级。滑动摩擦系数μs取值范围为0～1，设置16种工况进行模拟。采用颗粒最终稳定堆积高度h来表征堆积稳定性，堆积高度越高表明堆积稳定性越好。

2 等效滚动阻力的离散元模拟

2.1 接触模型

采用的接触模型是Iwashita等[26]提出的MDEM模型，如图4所示。该模型包括三部分：法向接触模型、切向接触模型和抗转动接触模型，该模型利用弹簧和阻尼来表征颗粒间各方向的接触力。商昆麒等[27]研究认为，基于滚动阻力模型建立的球形单元在计算时与复杂形态离散单元和颗粒簇单元相比，计算成本更具优势。

图4 MDEM模型

2.2 等效滚动阻力的建立

在古典摩擦定律中，滑动摩擦系数定义为滑动摩擦力与法向荷载的比值，是一个无量纲参数，取值范围一般在0～1之间，滚动摩擦系数与之不同，滚动摩擦阻力是一种阻碍物体发生滚动的力矩，滚动摩擦系数的物理意义为偏心距，是有长度量纲的。经典的滚动摩擦系数[28]定义如下：

(2)

其中：F为切向力；R为滚动圆盘的半径；N为法向荷载。根据力的平衡，滚动阻力矩M=F·R，滚动摩擦系数k就是法向荷载N的偏心距。

为便于分析，在进行离散元模拟时将滚动摩擦系数进行无量纲化处理，定义滚动摩擦阻力参数amur如下：

(3)

其中：Δ为颗粒间接触法向重叠深度，Δ=ra+rb-ds；ra、rb为圆形颗粒的半径；ds为两接触颗粒圆心间的距离。Δ、ra、rb、ds单位均是m。

最大滚动阻力矩定义如下：

fr max=amur·N·Δ

(4)

当总阻力矩超过最大滚动力矩fr max时，圆形颗粒发生滚动，反之，则不发生滚动。在进行模拟结果分析时，需将定义的滚动阻力参数amur转化成滚动摩擦系数μr，即μr=amur·Δ。通过程序计算输出的颗粒间法向接触力fn和切向接触力ft可以对颗粒间接触法向重叠深度Δ进行确定，经计算Δ=3×10-5m。

2.3 离散元模拟过程

基于软球模型，利用Fortran语言编写程序，建立颗粒离散元堆积模型，模拟圆形颗粒的堆积过程。颗粒材料的参数选取与有限元模型一致。

采用控制变量法模拟不同滑动摩擦系数μs和滚动摩擦系数μr下的颗粒堆积过程，研究等效滚动摩擦阻力与颗粒不规则形状之间的关系。离散元模拟过程与有限元模拟大致相同，主要分为两个阶段，如图5所示，模拟结果可直接输出堆积高度h，l为堆积塌落宽度。

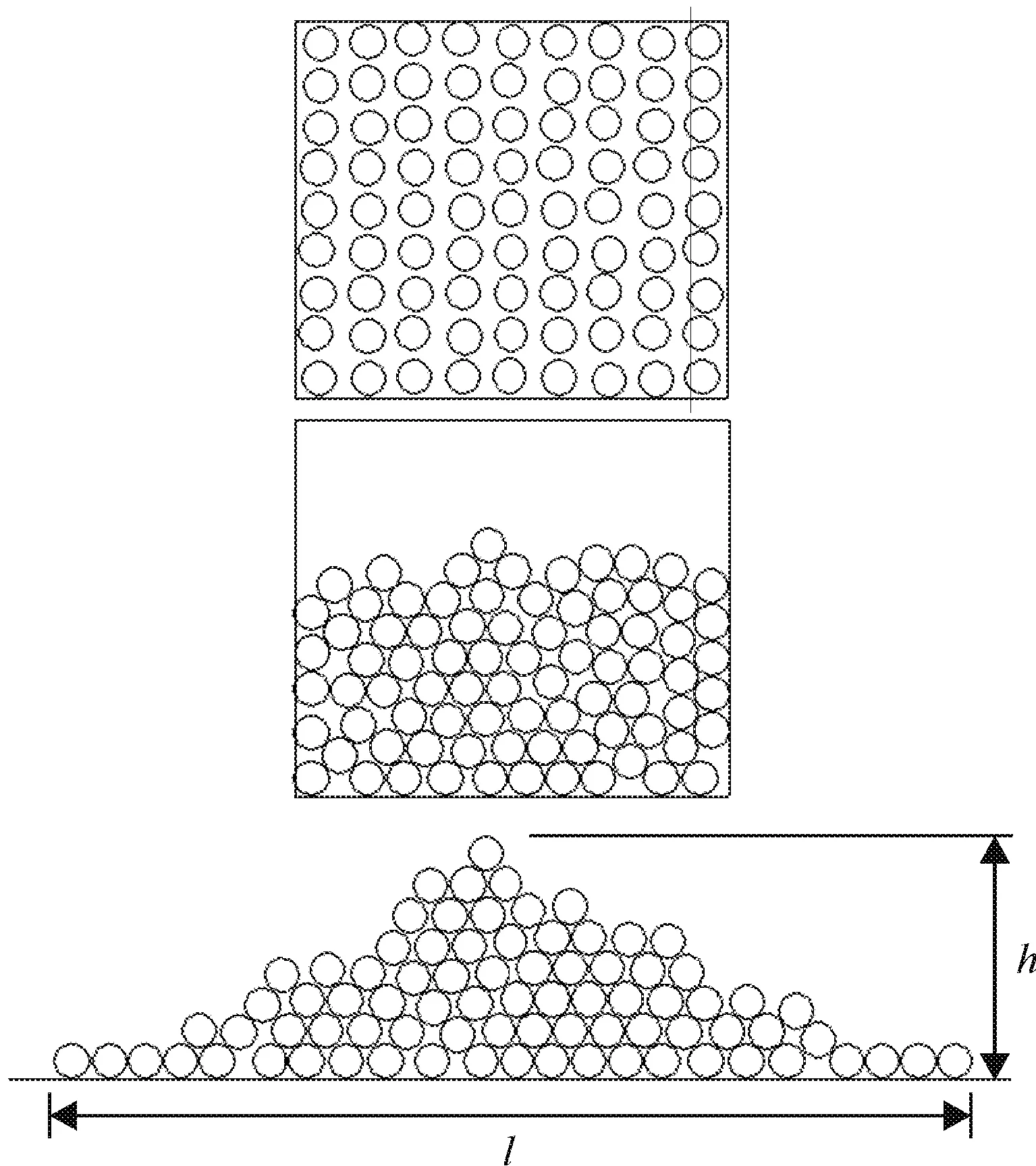
图5 离散元圆形颗粒堆积过程示意图

3 模拟结果分析

3.1 颗粒数量对堆积稳定性的影响

为探究颗粒数量对堆积稳定性是否存在影响，选取颗粒数量为81个、400个和1 024个共三种数量级，采用控制变量法，模拟滚动摩擦系数μr=0.15和滑动摩擦系数μs=0.5时，不同数量颗粒体系的堆积过程，三种数量颗粒堆积体的总体积相同。图6为μr=0.15时不同数量颗粒体系堆积状态随滑动摩擦系数改变的变化趋势，图7为μs=0.1时，不同数量颗粒体系的堆积状态对比。

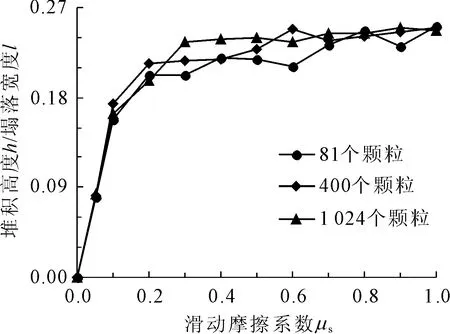
图6 μr=0.15时，三种数量颗粒体系堆积状态随滑动摩擦系数的变化趋势

图7 μr=0.15，μs=0.1时，三种数量颗粒体系堆积状态对比

将同一工况下，三种数量颗粒堆积体高宽比的最大值和最小值作差除以最小值，算出在滚动摩擦系数一定时，滑动摩擦系数对不同数量颗粒体系的影响程度，如表1所示。

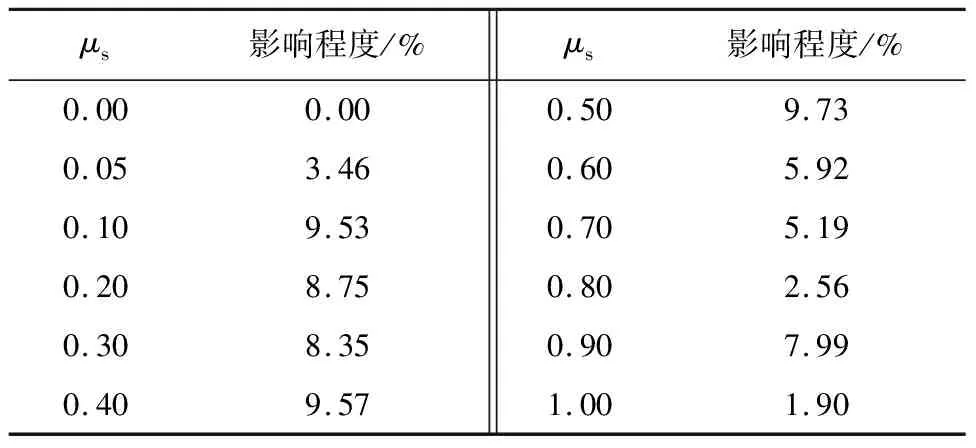
表1 变滑动摩擦下，颗粒数量对堆积状态影响程度

由表1可知，滚动摩擦系数为定值时，随着滑动摩擦系数的变化，颗粒数量对堆积状态的影响程度在10%内。

图8为μs=0.5时不同数量颗粒体系堆积状态随滚动摩擦系数改变的变化趋势，图9为μr=0.000 3时，不同数量颗粒体系的堆积状态对比。表2为滑动摩擦系数一定时，滚动摩擦系数对不同数量颗粒体系的影响程度。

图8 μs=0.5时，三种数量颗粒体系堆积状态随滚动摩擦系数的变化趋势

图9 μs=0.5，μr=0.000 3时，三种数量颗粒体系堆积状态对比

由表2可知，滑动摩擦系数为一定值时，随着滚动摩擦系数的变化，颗粒数量对堆积状态的影响程度在10%以内。综上，当颗粒体系总体积一定时，颗粒间摩擦特性对堆积稳定性的作用规律受颗粒数量变化的影响较小，因此为提高计算效率，在颗后续研究中，颗粒数量设定为81个。

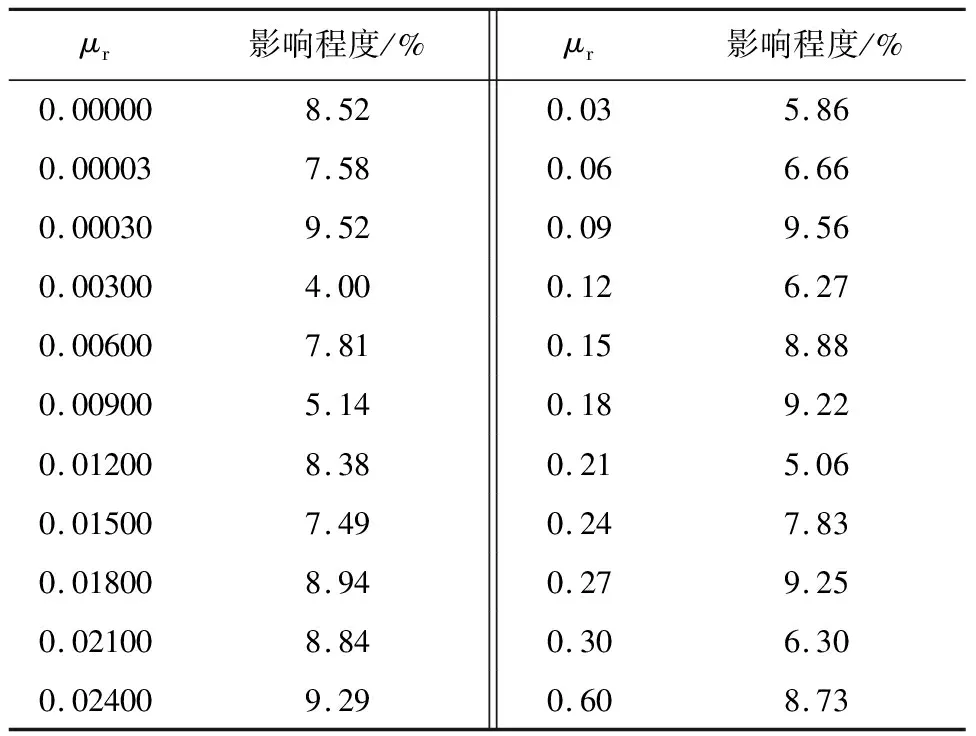
表2 变滚动摩擦下，颗粒数量对堆积状态影响程度

3.2 颗粒不规则形状对堆积稳定性的影响

有限元模拟中，颗粒在重力作用下自由运动，达到稳定状态后，形成颗粒堆，测量此时的堆积高度h，通过颗粒稳定堆积高度h表征颗粒堆积稳定特性。将四种形状的多边形颗粒在16组滑动摩擦系数μs下的堆积高度绘成滑动摩擦系数μs-堆积高度h变化曲线，如图10所示。

图10 多边形颗粒的滑动摩擦系数μs-堆积高度h曲线

从图10曲线可以看出，四种形状颗粒的堆积高度随滑动摩擦系数μs的增大整体呈增长趋势，且增长率在μs取值为0.0～0.3时较大，在μs取值为0.3～1.0时较小。滑动摩擦系数μs较小时，相同滑动摩擦系数μs下,形状系数s=0.777 6的颗粒的堆积高度h最高，其次是形状系数s=0.929 9的颗粒和形状系数s=0.952 1的颗粒，形状系数s=0.973 6的颗粒的堆积高度h最小，即颗粒形状棱角度越高，颗粒间的咬合互锁作用越强，越易形成稳定堆积体，且在滑动摩擦系数μs较小时，颗粒形状的不规则程度对堆积体稳定性的作用较明显,当滑动摩擦系数μs取值较大时，颗粒形状对堆积稳定性的影响较弱。

在图10中也可以看出，形状系数s=0.777 6的颗粒的堆积高度h受滑动摩擦系数μs影响的范围在0.0～0.2，形状系数s=0.929 9的颗粒的堆积高度h受滑动摩擦系数μs影响的范围在0.0～0.3，形状系数s=0.952 1的颗粒的堆积高度h受滑动摩擦系数μs影响的范围在0.0～0.4，而形状系数s=0.973 6的颗粒的堆积高度h受滑动摩擦系数μs影响的范围在0.0～0.7，即颗粒棱角度越高，滑动摩擦系数μs对其堆积稳定性产生影响的取值范围越小。分析原因，认为是颗粒的不规则形状使得颗粒在发生滚动时需要较大的切向力，当切向力增大到等于接触面的临界滑动摩擦力时，颗粒的运动形式就从滚动转化为滑动，因此滑动摩擦系数μs的改变对形状不规则程度较大的颗粒的作用不再明显，这一现象在孙珊珊等的研究[29]中也有所证实。

3.3 滚动阻力对堆积稳定性的影响

在离散元模拟中，滚动摩擦系数取值范围为0.0～1.0，设置47组滚动摩擦系数μr，模拟不同滚动摩擦系数μr下的颗粒堆积情况。选取滑动摩擦系数μs为0.1,0.4和0.9三组试验数据进行对照分析绘成曲线，如图11所示。

图11 滚动摩擦系数μr-堆积高度h曲线

从图11可以看出，随着滚动摩擦系数μr的增大，三条曲线整体呈增长趋势，且滑动摩擦系数μs曲线在滚动摩擦系数μr较小时增长率较大，随着滚动摩擦系数μr的继续增大，三条曲线的曲率逐渐减小，并有逐渐趋于0.0的趋势，由此说明，滚动摩擦系数μr仅在一定取值范围内对颗粒材料堆积稳定性产生显著影响；颗粒材料的滑动摩擦系数μs不同，滚动摩擦系数μr对其堆积稳定性产生影响的参数取值范围也有差别，而且可以看出滑动摩擦系数μs=0.1的颗粒稳定堆积高度随滚动摩擦系数μr的增加呈阶梯式增长，分析原因，认为是粒间滑动摩擦系数μs较小的颗粒在堆积过程中的运动以滑动为主，对滚动阻力不敏感，当滚动摩擦系数μr有明显增加时才会提高其堆积稳定性，从而形成了阶梯式的堆积高度增长曲线。

为研究颗粒形状不规则程度与等效滚动阻力间的关系，设置滚动摩擦系数μr=0.000，0.027，0.060和0.300四组工况进行离散元模拟，将模拟结果进行拟合绘成曲线如图12所示。

图12 四种滚动摩擦系数下，滑动摩擦系数μs-堆积高度h曲线

从图12中可以看出，滑动摩擦系数μs为0.0时，堆积高度为0.22 m，与颗粒直径相同，说明此时颗粒只堆一层，无法形成稳定堆积体；滚动摩擦系数μr为0.0时，滑动摩擦对颗粒材料的堆积稳定性几乎不起作用，滚动摩擦系数不为0.0时，颗粒稳定堆积高度随滑动摩擦系数μs的增大而增大，说明颗粒材料的堆积稳定性受滑动摩擦和滚动摩擦共同影响。

同时，滚动摩擦系数μr=0.3的曲线在滑动摩擦系数μs在0.0～0.2范围内曲率较大，滚动摩擦系数μr=0.06的曲线在滑动摩擦系数μs在0.0～0.3范围内曲率较大，当滑动摩擦系数μs继续增加超过此范围时，曲线的曲率迅速减小并趋于0.0；而滚动摩擦系数μr=0.027的曲线在滑动摩擦系数μs在0～1范围内一直呈现明显增长趋势。由此说明，当滚动摩擦系数μr不为0.0时，滑动摩擦对颗粒堆积稳定性的影响随滚动摩擦系数μr的增大而减小。这一结论与有限元中多边形颗粒堆积过程模拟得到的规律相类似，Oda等[10]也认为滚动阻力不仅与颗粒间的接触有关，还与颗粒形状密切相关，由此说明，颗粒形状的不规则程度可用等效滚动阻力进行表达。

3.4 等效滚动阻力与颗粒不规则形状相关关系

将有限元模型中多边形颗粒的稳定堆积结果和离散元模型中不同滚动摩擦系数μr下的圆形颗粒的稳定堆积结果进行对比。通过调整滚动摩擦系数μr的参数值，确定与四种形状颗粒对应的等效滚动摩擦系数，将与四种形状颗粒的模拟结果较为近似的工况数据用指数函数进行拟合，绘制成滑动摩擦系数μs-堆积高度h曲线，见图13。

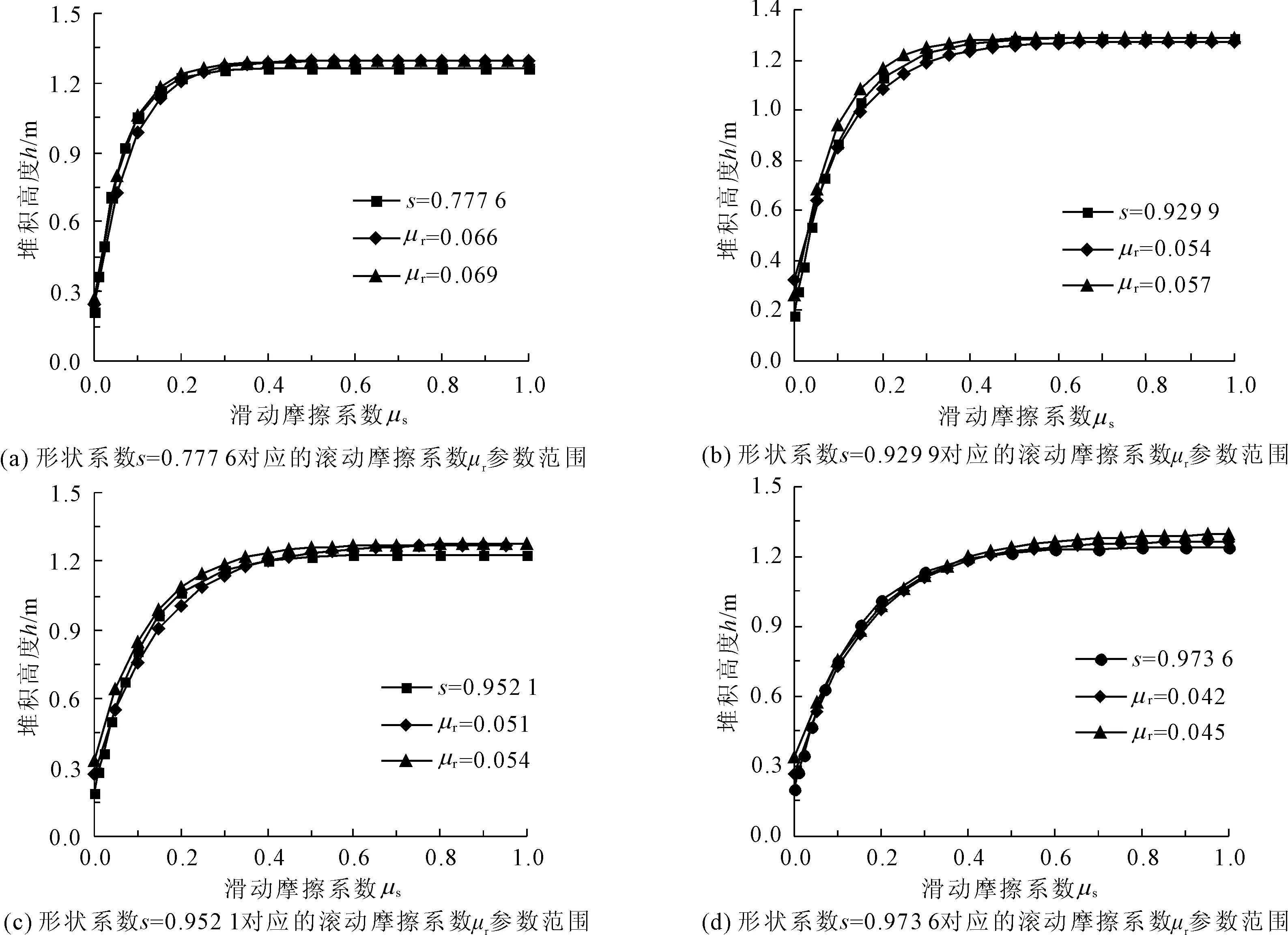
图13 四种颗粒形状对应的等效滚动阻力

由此可确定，与形状系数s=0.777 6对应的滚动摩擦系数范围是μr=0.066～0.069，与形状系数s=0.929 9对应的滚动摩擦系数范围是μr=0.054～0.057，与形状系数s=0.952 1对应的滚动摩擦系数范围是μr=0.051～0.054，与形状系数s=0.973 6对应的滚动摩擦系数范围是μr=0.042～0.045。因此，颗粒形状的不规则特性可在一定范围内通过滚动摩擦系数μr来表征。

4 结 论

(1)颗粒形状的不规则特性在滑动摩擦系数取值为0.0～0.3范围内对颗粒堆积稳定性影响显著，在此范围内，相同滑动摩擦系数下，颗粒形状越不规则，稳定堆积高度越高；滑动摩擦系数取值超过0.3时，不同形状颗粒的稳定堆积高度无明显差异。

(2)滑动摩擦系数对颗粒堆积稳定的敏感性受颗粒形状影响，即颗粒形状越饱满，对稳定堆积高度影响显著的滑动摩擦系数取值影响范围越大：正三角形颗粒对稳定堆积高度敏感的滑动摩擦系数范围是0.0～0.2，正五边形颗粒的范围是0.0～0.3，正六边形颗粒的范围是0.0～0.4，正八边形颗粒的范围是0.0～0.7。

(3)颗粒形状的不规则特性可在一定范围内通过滚动摩擦系数来表征。正三角形颗粒对应的滚动摩擦系数可取值范围0.066～0.069，正五边形颗粒的可取值范围0.054～0.057，正六边形颗粒的可取值范围0.051～0.054，正八边形颗粒的可取值范围0.042～0.045。