河道堤防物理力学参数反演计算模型的改进及应用

陆占杰

(盘山县农业水利事务服务中心，辽宁 盘锦 124010)

河道堤防物理学参数是其治理工程稳定设计的重要参数和依据，参数确定的精准度直接影响河道治理工程的稳定性[1]。传统河道堤防物理学参数主要通过现场试验进行确定，这种方式的优点在于可以真实有效地反映河道堤防的实际情况，但缺点在于很难对整个河段物理力学参数进行确定，且对于裂隙较大的河道堤防天然岩石而言，这种方式确定的堤防物理学参数具有较为明显的误差[2]。当前，结合原位现场观测，通过力学反演模型对其河道堤防力学参数进行全面反演计算的方法在国内许多河道治理工程设计中得到应用[3- 9]，这种方法可实现河道整个治理段力学参数的全要素反演，通过设定反演模型参数，对其进行反演，并结合现场观测数据，对模型反演精度进行分析，从而确定合理的模型力学参数反演区间。但该方式的缺点在于很难实现河道力学参数的反演目标优化，需要进行大量的试错计算，才能得到较为合理的河道力学参数反演区间。为提高河道堤防力学参数的反演精度，本文结合目前在目标优化求解应用较好的自适应函数[10- 15]，对传统反演模型进行目标函数的优化求解，从而对模型进行改进，考虑改进后模型的反演精度，以盘锦地区某河道治理工程为实例，结合现场观测数据，对比分析改进前后反演模型的精度。研究成果对于河道堤防治理工程设计具有重要参考价值。

1 模型反演及改进原理

模型的反演原理在于通过现场观测数据，建立样本数据系列，结合小波分析原理对样本序列进行训练结合，并将训练后的样本数据系列，最大程度地与目标函数进行拟合，对于河道堤防物理学参数而言，其地质参数是主要的物理训练样本，而其目标函数主要为坝顶下沉和位移量，其样本训练方程为：

(1)

式中，τ、α—纵向、横向变量状态值；t—时段步长。采用小波变换函数对方程进行变换求解：

Ψ(t)=cos(1.75t)e(-t2/2)

(2)

模型控制节点计算方程为：

(3)

式中，φ(j)—各控制节点的函数值；aj—反演模型函数初始状态值；i—控制节点单元个数；wij—不同权重变量值；τj—控制节点计算步长。模型目标函数为：

(4)

式中，k—反演的目标参数的数目。

本文引入自适应函数对反演模型目标函数进行优化求解，其函数优化方程为：

(5)

(6)

(7)

(8)

式中，E—采用自适应函数后的优化目标函数值。

2 实例应用

2.1 堤防工程概况

以盘锦地区某河道治理工程为具体实例，探讨改进前后模型在河道堤防力学参数的反演精度，该治理河道堤防全长及宽度分别为5.5km和35m，河道底部高程在2.5～3.5m之间。堤顶高程现状条件下为11.5m，迎水面堤防坡比约为1∶2.5，堤防地层主要以混合岩和大理岩为主，局部为安山岩及松散堆积层组成。结合现场观测试验对河道堤防位移和沉降进行观测，其对应位移和沉降点力学参数测定值见表1。

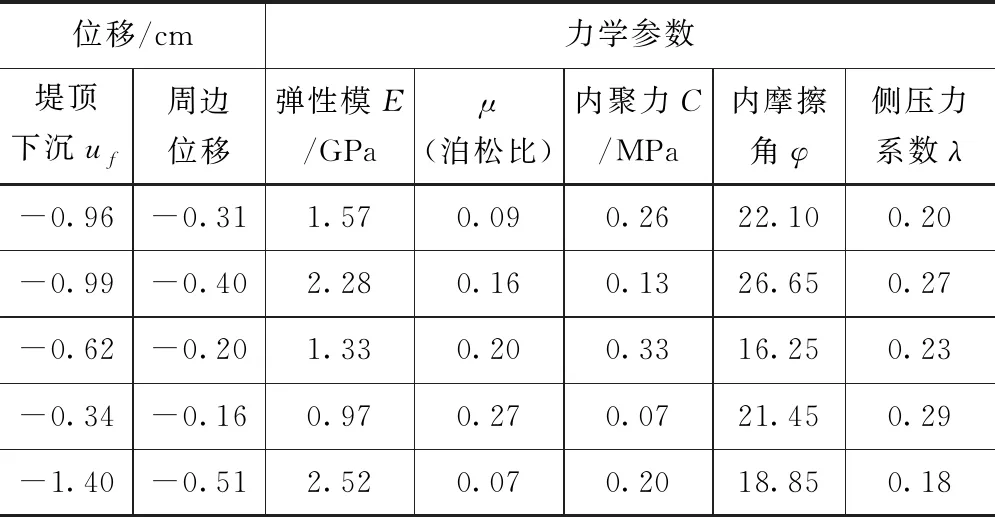
表1 各点位位移及沉降对应的力学参数

2.2 模型反演参数及取值范围的确定

结合原位观测试验对模型参数取值范围进行分析，各力学参数反演区间见表2。

表2 河道堤防力学反演参数取值区间

采用原位现场观测试验方式，对各监测点位位移和沉降下的弹性模量、泊松比、内聚力、内摩擦角及侧压力系数进行分析，从分析结果可看出，不同取值水平下弹性模量总体呈现递增变化，变化最高弹性模量为3.3GPa，沉降和位移最低点位其弹性模量为1.1GPa。各监测点位的泊松比在0.1～1.0之间，高监测点位可达到泊松比的最高值。内聚力和内摩擦角对于河道堤防稳定性至关重要，从各取值水平可看出，其内聚力变幅总体较低，而内摩擦角变幅较高。侧压力系数在各取值水平下总体变化较为稳定。

2.3 不同模型参数计算方案反演精度分析

采用自适应函数对模型目标函数进行优化后，采用正交试验方式对模型参数进行优化，各组优化试验结果见表3。

表3 正交试验下不同组序下模型反演精度

通过正交试验对不同试验组序下的参数反演精度可看出，随着试验训练组序的增加，模型反演计算的堤防沉降和边波位移总体呈现递减变化，这主要是因为引入自适应函数对模型目标进行优化求解后，随着训练样本系列的增加，其逐步趋于最优目标求解值。在初始样本训练组序下，模型对于河道堤防力学参数反演误差较大，而随着训练样本组序的增加，模型优化求解收敛度逐步增加，模型误差分布降低，当训练试验组序达到最高值时，其模型目标函数具有最优解。

2.4 改进前后模型反演精度对比

结合5组现场观测位移和沉降数据，分别采用改进前后模型对研究河道堤防的参数进行反演计算，确定反演参数值，并将参数代入到反演模型，对目标函数进行求解计算，对比5组观测试验下的反演精度，模型参数值见表4，改进前后模型反演精度如见表5—6。

表4 不同试验组序下模型参数值

表5 改进模型目标函数反演精度

在各组监测点位观测数据可看出，改进模型后在各组反演参数下其沉降值和边坡位移和观测点之间的边坡位移和沉降之间误差总体可控制在20%以内，具有较好拟合度，通过各组训练样本分析其拟合度可达到0.5以上，通过对反演模型的目标函数进行优化求解后，加速和优化了模型的收敛精度，从而改善模型求解的精度。改进前反演模型在河段堤防各点位目标求解值和现场点位观测之间的误差都明显高于改进后的反演模型，且部分点位误差值高于30%。通过以上分析采用改进后的模型，由于引入自适应函数对目标进行优化求解，总体好于改进后模型。

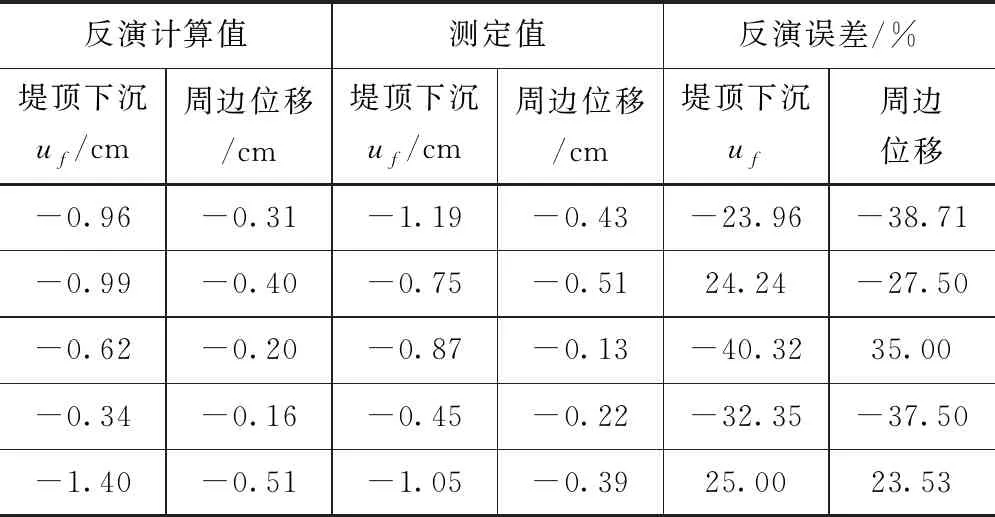
表6 改进前模型目标函数反演精度

3 结论

(1)在采用自适应函数进行目标优化求解时，需要确定河道堤防力学反演参数的取值区间，一般建议以原位观测试验时河道堤防最高和最低观测点位的试验参数作为其取值区间。

(2)在进行模型样本训练时，随着训练组数的增加其目标拟合度将逐步提高，一般建议在进行河道堤防力学参数反演模型构建时，试验组数不低于20组，从而可提高参数反演模型的收敛度；

(3)本次试验的河段属于中小型河道，且地质类型相对较为简单，对于地质较为复杂的大型河道改进模型的适用性还需要进一步探讨。