A review on SRAM-based computing in-memory: Circuits,functions, and applications

Zhiting Lin, Zhongzhen Tong, Jin Zhang, Fangming Wang, Tian Xu, Yue Zhao, Xiulong Wu, Chunyu Peng,Wenjuan Lu, Qiang Zhao, and Junning Chen

School of Integrated Circuits, Anhui University, Hefei 230601, China

Abstract: Artificial intelligence (AI) processes data-centric applications with minimal effort. However, it poses new challenges to system design in terms of computational speed and energy efficiency. The traditional von Neumann architecture cannot meet the requirements of heavily data-centric applications due to the separation of computation and storage. The emergence of computing in-memory (CIM) is significant in circumventing the von Neumann bottleneck. A commercialized memory architecture, static random-access memory (SRAM), is fast and robust, consumes less power, and is compatible with state-of-the-art technology. This study investigates the research progress of SRAM-based CIM technology in three levels: circuit, function, and application. It also outlines the problems, challenges, and prospects of SRAM-based CIM macros.

Key words: static random-access memory (SRAM); artificial intelligence (AI); von Neumann bottleneck; computing in-memory(CIM); convolutional neural network (CNN)

1.Introduction

Recently, with the breakthrough of key technologies such as big data and artificial intelligence (AI), emerging intelligent applications represented by edge computing and intelligent life have emerged in the trend of the era of rapid development[1,2]. These emerging intelligent applications often need to access the memory frequently when dealing with events. However, von Neumann architecture is the most commonly used architecture for data processing, which is implemented by separating memory banks and computing elements. Massive volumes of data are exchanged between the memory and processing units, which consume large amounts of energy. Furthermore, the memory bandwidth limits the computing throughput. The resulting memory limitation increases energy wastage and latency and decreases efficiency.This limitation is more severe in resource-constrained devices. Therefore, it is important to explore solutions to overcome the issue of the “memory wall.”

As a computing paradigm that may address the von Neumann bottleneck, researchers have proposed the computing in-memory (CIM) technology. The so-called CIM is a new architecture and technology for computing directly in memory. It breaks through the limitation of traditional architecture, optimizes the structure of storage unit and logic unit, realizes the integration of storage unit and logic unit, and avoids the cumbersome process of transmitting data to processor register for calculation and then back to memory, thus significantly reducing the delay and energy consumption of the chip[3]. Research on static random-access memory (SRAM) has become an active topic in CIM for the robustness and access speed of its cells.

To improve the performance of the SRAM-based CIM, the SRAM bitcell structure has been modified and auxiliary peripheral circuits have been developed. For example, read–write isolation 8T[4,5], 9T[6−8], and 10T[9−11]cells were proposed to prevent the storage damage caused by multirow reading and calculation. Transposable cells were proposed to overcome the limitations of storage arrangement[12−14]. Peripheral circuits, such as word[15,16], bit[10], line digital-to-analog conversion (DAC), redundant reference columns[1,5], and multiplexed analog-to-digital conversion (ADC)[17], were proposed to convert between analog and digital signals. With these modified bitcells and additional peripheral circuits for SRAM CIM,researchers have achieved various computational operations,including in-memory Boolean logic[5,7,18−27], content-addressable memory (CAM)[5,19,20,28,29], Hamming distance[8], multiplication and accumulation (MAC)[1,2,9,10,15,17,30−34], and the sum of absolute difference (SAD)[35,36]. These in-memory operations can expedite the AI algorithms. For example, Sinangilet al. implemented a multibit MAC based on a 7-nm FinFET technique to accelerate the CNN algorithm, which achieved a recognition accuracy of 98.3%[37,38]. Agrawalet al. proposed a novel “read–compute–store” scheme, wherein the XOR calculation results were used to accelerate the AES algorithm without having to latch data and perform subsequent write operations[18].

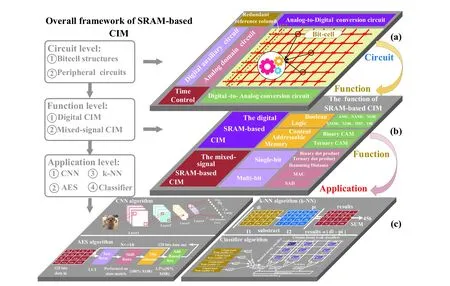
Fig. 1. (Color online) Overall framework of static random-access memory (SRAM)-based computing in-memory (CIM) for the review: (a) various functions implemented in CIM, (b) operation functions realizable with CIM, and (c) application scenarios of CIM.

As illustrated in Fig. 1, we reviewed three levels of SRAMbased CIM: circuit, function, and application. The circuit level is reviewed from two aspects: 1) bitcell structures, which include read–write separation structures, transposable structures, and compact coupling structures, and 2) peripheral auxiliary circuits, which include analog-to-digital conversion circuits, digital-to-analog conversion circuits, redundant reference columns, digital auxiliary circuits, and analog auxiliary circuits (Fig. 1(a)). The second level is reviewed from two aspects: 1) pure digital CIM, which includes Boolean logic and CAM, and 2) mixed-signal CIM functions, which include MAC,Hamming distance, and SAD (Fig. 1(b)). The third level is mainly reviewed from the aspects of the application of the accelerating CNN, classifier, k-NN, and AES algorithms (Fig. 1(c)).Finally, the challenges and future development prospects of SRAM-based CIM are discussed from these three levels.

2.Memory cell in static random-access memory(SRAM)-based computing in-memory (CIM)

In the core module of the SRAM, the memory cell occupies most of the SRAM area. Irrespective of the complexity of operations implemented in the memory unit, the primary challenge is to fully leverage the memory cells. In this section,we analyze and summarize the cell structures in the SRAMbased CIM. Additionally, we compare the performances of the reconstructed SRAM cell and the traditional structure and discuss the possible research direction of CIM in terms of the cell structure.

2.1.Structure of the 6T cell

2.1.1. Standard 6T-SRAM structure

Standard 6T structures have been adopted in most system-on-chips (SoCs) for their high robustness and access speed. Previous studies on CIM, including Refs. [15, 16, 19, 20,24−26, 29, 33, 35, 39−53] and Ref. [34], used standard 6T cells considering the area overhead. Fig. 2(a) illustrates a schematic of the standard 6T SRAM cell. The 6T storage cell is composed of two P-channel metal–oxide–semiconductors(PMOSs) and four N-channel metal–oxide–semiconductors(NMOSs), in which P1, N1, P2, and N2 constitute two crosscoupled inverters to store data stably. To perform CIM with the conventional 6T SRAM cell, the operands are commonly represented by the word line (WL) voltage and storage node data. The processing results are often reflected by the voltage difference between BL and BLB.

2.1.2. Dual-split 6T cell

Khwaet al.[1,2]designed a 6T cell with double separation(WL separation and ground line separation), as shown in Fig.2(b), which is in contrast to the standard 6T structure. When the dual-split 6T cell performs basic SRAM read and write functions, it connects the left WL (WLL) and right WL (WLR), as well as ground, CVSS1, and CVSS2. The read and write operations are consistent with those of the standard 6T cells.However, this structure can achieve more sophisticated functions owing to the separated WL and GND. The structure allows the use of different voltages to represent various types of information.

2.1.3. 4+2T SRAM cell

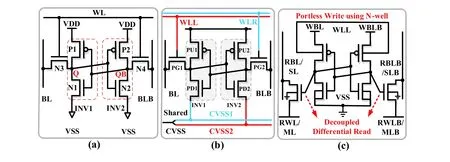
Fig. 2. (Color online) (a) Standard 6T SRAM cell, (b) dual-Split 6T SRAM cell, and (c) 4+2T SRAM cell.

Fig. 3. (Color online) SRAM cells with separated read and write: (a) standard 8T SRAM bit-cell, (b) 7T SRAM cell, (c) 9T SRAM cell, and (d) 10T SRAM cell.

Donget al.[20]proposed a 4+2T SRAM cell (Fig. 2(c)). The 4+2T memory cells were used to decouple data from the read path. The read operation was similar to that of the standard 6T SRAM, but the write operation was different as it adopted the N-well as the write word line (WWL), and the source ends of two pull-up PMOS were used as the write bit line(WBL) and write bit line bar (WBLB). The design was implemented in the deep-decomposed channel process, where the bulk effect of the circuit was more significant. To write data,the threshold voltage of the PMOS can be significantly altered by changing the N-well and PMOS source voltages.During the application of CIM, different voltages on the WL and storage node represent the different operands.

2.2.Cell structure with additional devices for SRAMbased CIM

The simple 6T structure cannot realize complex computing operations and does not fully meet the requirements of CIM. Therefore, studies on CIM have modified the traditional 6T structure, which can be roughly divided into the following four categories.

2.2.1. SRAM cells with separated read and write paths

Compared with the 6T cell, SRAM cells with separated read and write do not suffer from reading–writing disturbances; hence, within the memory array, it can simultaneously activate multiple read WLs to complete the operation. These cells contain a standard 6T cell and an additional read port composed of extra transistors to separate read and write. The write operation is similar to that of a traditional 6T cell. For the read operation, these cells can read data through a read bit line (RBL) discharge or charge.

Fig. 3(a) presents a schematic of a standard 8T cell,where M2 and M1 form an additional read port. A large number of pioneering works have used standard 8T cells to complete CIM operations, including a multibit dot-product engine for computing acceleration[3], X-SRAM[18], and double WLs SRAM[5]for Boolean logic operations, a 7-nm CIM SRAM macro for multibit multiply multibit[37,38], and a computational SRAM (C-SRAM) for vector processing[54]. To reduce the area cost, Jiang Hongwuet al.[55]proposed a 7T cell to complete the dot product operation, as shown in Fig. 3(b). To achieve better performance and execute more complex operations, Srinivasaet al. utilized 9T SRAM cells to perform CAM operations[6]. Fig. 3(c) presents a schematic of the 9T SRAM cell. In Ref. [8], Aliet al. completed the Hamming distance based on a 9T SRAM cell. In Refs. [9, 10, 56, 57] and Ref. [17],10T SRAM cells were used to perform CIM of the dot product and XONR, as shown in Fig. 3(d). These studies demonstrated the advantages of the read–write separation structure in CIM, but the additional transistors also reduced the storage density.

2.2.2. SRAM cells based on capacitive coupling

SRAM cells based on capacitive coupling add additional capacitances inside the cell to perform the operations. Jianget al.[31,58]proposed a C3SRAM (capacitive-coupling computing)cell, which is composed of a standard 6T cell, a pair of transmission transistors controlled by the storage data from the gate,and a capacitor, as shown in Fig. 4(a). In contrast to C3SRAM,Jia[59,60]and Valaviet al.[61]proposed a multiplying bitcell (MBC) circuit, where the transmission transistors were controlled by the storage data from the drain or the source, as shown in Fig. 4(b). These cells can execute a dot-product operation between the input vectors and the stored weight. The calculation result is represented by the number of capacitors storing charge. Therefore, cells based on capacitive coupling are less prone to process variations. However, the introduction of capacitance into the memory cell increases the overall power consumption and area overhead.

Fig. 4. (Color online) SRAM cells based on capacitive coupling: (a) C3SRAM bitcell and (b) M-BC bitcell.

Fig. 5. (Color online) (a) Transposable bitcell contains two pairs of access transistors and (b) separated read–write transposable bit cell. (c) Schematic of the transposable 10T bit bitcell.

In Refs. [31, 58], the capacitance in the cell can be directly coupled and shared through the MBL. However, in Refs. [59, 60 ], the capacitors inside the unit need to be coupled with each other through additional switches. Therefore, in the latter work, additional transistors need to be introduced, which increases the area of the cell. In the selection of capacitance type, Refs. [31, 58] selected MOSCAP which constitutes 27% of the bitcell area. However, Refs. [59, 60] selected MOMCAP that is formed using metal-fringing structures.MOMCAP can be placed on the top of the cell, so there is no additional area overhead. However, compared with MOSCAP,MOMCAP has a lower capacitance density and is not suitable for large capacitances.

2.2.3. Transposable SRAM cell

Fig. 5 presents three different forms of transposable bitcells: 1) Wanget al.[12,13]proposed a transposable bitcell containing two pairs of access transistors, as shown in Fig. 5(a).There are two types of writing and reading in the basic SRAM functions of this structure: the one used by columns and the other by rows. When performing CIM operations, the structure can achieve two-directional computing. 2) Similarly, Jianget al.[14,55]proposed a separated read–write transposable bitcell, as shown in Fig. 5(b). This structure can choose to read data by rows or columns. In addition, this structure can perform CIM operations on both row and column dimensions simultaneously using a row bit line (R_BL) or column bit line (C_BL). 3) Linet al. proposed a 10T bitcell to avoid vertical data storage and improve the stability of CIM, as shown in Fig. 5(c)[11]. In this study, vector logic operations can be performed with multirow or multicolumn parallel activation, and CAM can be achieved in two directions. Because of the row–column symmetry, these cells break the limitations of conventional SRAM storage arrangements. Thus, the algorithm of forward and backward propagations can be flexibly applied to them.

2.2.4. Compact coupling structure

The basic reading and writing operations of the compact-coupling structure are consistent with traditional SRAM.However, exclusive and independent structures have been developed for CIM operations. Yinet al.[17]proposed a 12T cell,as shown in Fig. 6(a), where T1–T6 constitute a 6T SRAM circuit, T7–T10 perform XNOR functions, and T11 and T12 decide the execution of the XNOR function. Suet al.[43,62]proposed a two-way transpose multibit cell structure (Fig. 6(b))that contains a common functional operation unit used by 16 6T cells to execute multiplication in the vertical or horizontal direction.

Both structures are based on traditional 6T cells, which perform operations by adding compact-coupled computing units. This strategy can maintain the basic read and write capabilities of SRAM while allowing it to perform complex operations. However, the compact-coupling module also increases the area overhead and complexity of the peripheral control circuit.

Fig. 6. (Color online) Compact coupling structure: (a) 12T cell and (b) two-way transpose multibitcell.

Table 1. Static random-access memory (SRAM) bitcells in CIM.

Table 1 summarizes various types of SRAM-based CIM bitcell. It was found that the area efficiency of the previous study was related to the structure of the basic cells. In CIM,two main approaches are used to design the bitcell: 1) maintaining the standard 6T and 2) reconstructing basic units by adding additional transistors or capacitors. Currently, the main purpose of cell design in CIM is to realize novel operations, and the automatic restoration of operation results is not realized. In the future, the unit design will focus on the processing of operation results.

3.Peripheral auxiliary circuits of the SRAM-based CIM

Depending on the basic cells in the array, only limited digital computing functions can be achieved. Peripheral circuits, such as high-precision ADC, weight processing, generation of reference voltage, pulse modulation, and near memory multiplication, must be used with the SRAM system to achieve high-performance memory operations or analog domain computation.

3.1.Analog-to-digital conversion (ADC) circuit

An ADC circuit is indispensable in processing computational results in an array (mostly analog value represented by the BL voltage). It has two main roles: 1) quantifying the BL voltage and 2) weighting the BL voltage.

3.1.1. Quantifying BL voltage

As shown in Fig. 7(a), it is an asymmetrically sized sense amplifier (SA)[18]. This circuit is different from the traditional SA, which is only used to read data. If the MBL in the circuit is set to be larger than MBLB, the BL will discharge faster than the BLB under the same conditions. This difference in the discharging speed distinguishes the two cases of input ‘01’ and‘10’ in the Boolean logic. Thus, in a single memory read cycle,a class of bitwise Boolean operations can be obtained by reading directly from the asymmetrically sized SA outputs.

Sinangilet al.[24,37]proposed a 4-bit flash ADC. This ADC uses SA to save the area and reduce the power consumption.Each 4-bit flash ADC uses 15 SAs simultaneously and quantizes the analog voltage of the RBL by setting 15 different reference voltage levels (Fig. 7(b)).

In Ref. [32], Siet al. used several capacitors with different values to generate different reference voltages to quantify the analog voltage of the RBL. RBL shares its charge with the capacitor array after multicycle operations (Fig. 7(c)). In this design, capacitors with different values are sequentially connected to one of the two ends of the SA through a switch;that is, a stepwise comparison is performed through multiple operation stages to quantify the analog voltage of the RBL.

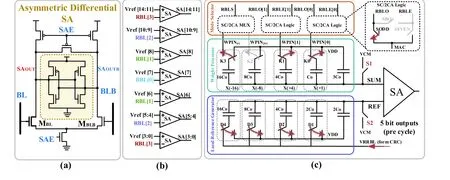
Fig. 7. (Color online) (a) Asymmetric differential sense amplifier (SA), (b) flash ADC, and (c) successive approximation ADC.

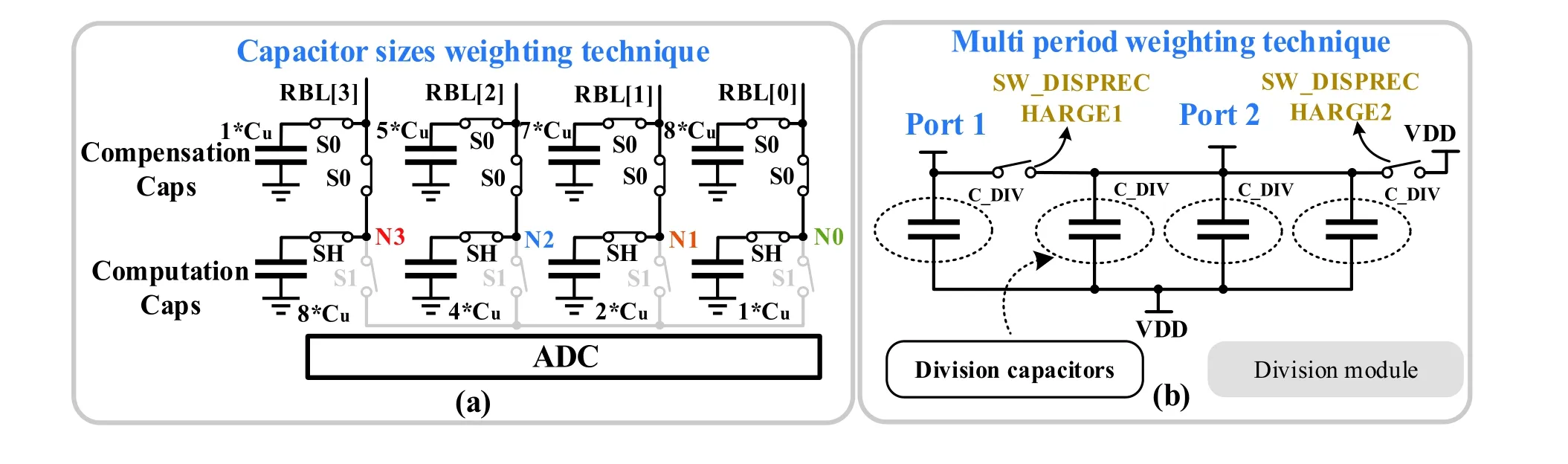
Fig. 8. (Color online) (a) Weighted array with different capacitor sizes and (b) multi-period weighting technique using capacitors of the same size.

The quantifying circuits process the final calculation result, which is especially important for the calculation accuracy of the entire system. Most researchers choose flash ADC[14,37,38,55]or successive approximation ADC[44,51,52,60,63]to quantify the BL voltage. Flash ADCs usually require multiple comparators and reference voltages; thus, under the same bit-accuracy, the area and power consumption of flash ADC is relatively larger than SAR ADC. Sometimes a high-accuracy flash ADC may be larger than the whole array. SAR ADC only needs one comparator to complete the quantization operation. However, it needs multiple cycles for comparison. Consequently, its speed is far lower than that of flash ADC. To select the type of ADC in CIM, the tradeoff between quantization accuracy and the overhead of area power consumption is considered first. For example, the C3SRAM used flash ADC with multiple comparators and voltage references achieving a relatively high 1638 GOPS throughput[58]. The ADC consumed 15.28% of the area and 22% power of the whole chip.In this work, the 256-row can be activated for dot-product calculation; thus, the full resolution of partial convolution results was 8-bit. However, considering the area, power, and latency, a lower flash ADC was used with 5-bit accuracy design that was still able to maintain the final accuracy. In contrast, the authors in Ref. [57] used SAR ADC achieving a throughput of 8.5 GOPS, which consumed 43.1% of the area and 24.1% of the power of the entire chip. From the presented data, this SAR ADC seems to have larger area and power than the above-mentioned flash ADC. However, in this work,it had 8-bit accuracy to increase the inference accuracy. To reduce the interference of PVT, the SRAM-based CIM architecture needs to be integrated with ADC. Therefore, it is significantly important for the design of ADC in CIM works.

3.1.2. Weighting BL voltage circuits

One of the weighting BL voltage circuits is the capacitor array weighting circuits. It has a higher linearity, which is often used when high-precision operations are required. Capacitor array weighting techniques are broadly grouped into two categories:

2) Weighting by sharing charge across multiperiod operations, as shown in Fig. 8(b). In Ref. [64], the parasitic capacitance on the BL was the same as that of C_DIV in the capacitor array, so that the charge was shared equally among the capacitors. When 1/8 weighting was required, in the first period, the BL was connected to port 2 achieving the charge sharing with three C_DIVs. Thus, the voltage decreased to 1/4. In the second period, the BL was connected to port 1, and the shared charge was divided equally. Therefore, the original charge was ultimately divided into 1/8 of the original charge.Charge can be shared in multiperiod operations in a similar manner to achieve other weights.

Fig. 9. (Color online) Schematic of the column-wise GBL_DAC circuit: (a) Circuit of the constant current source, (b) two-stage MUX, and (c) waveform of the column-wise GBL_DAC circuit. (d) Schematic and waveform of the pulse height modulation circuit.

The two types of weighting techniques have their demerits. In the first technique, the capacitance increases exponentially with the number of input bits, which increases the area overhead exponentially. However, in that work its unit of computation capacitance is formed by the inherent cap of the sense amplifier (SA) inside the 4-bit Flash ADC, which saves area and minimizes the kick-back effect. Moreover, it is difficult to realize in the manufacturing process. In the second technique, the capacitance of the circuit remains unchanged.However, multiple operation periods are required to complete the weighting, which decreases the computation speed. In general, whether it is the equivalent capacitance of SA, MOMCAP or MOSCAP, if there has a large capacitance in the CIM system, the robustness of the operations will have a certain impact.

3.2.Digital-to-analog (DAC) conversion circuit

The purpose of the DAC circuit is to convert a digital input into the corresponding analog quantity as the pulse width or pulse height. The BL voltage can be decreased or increased proportionately by controlling the pulse width or pulse height in proportion to the digital input. The precise generation of these widths or heights is crucial to multibit calculation.

For example, for an input of 6 bits, the circuit design requires 64 different pulse widths. Generating such a variety of pulse widths in the memory consumes an immense area and power. Therefore, the solution to this problem requires a delicate circuit. Biswaset al.[10]proposed a global read bitline(GBL) DAC circuit consisting of a cascade PMOS stack biased in the saturation region to act as a constant current source(Fig. 9(a)) and a two-level data selector (Fig. 9(b)). The circuit controls the opening time of the transmission gates according to the input data so that the bitline is charged to the corresponding voltage value. With the traditional scheme, it required 64 types of signals and 64 : 1 MUX if the input is 6-bit(XIN [5:0]). However, in Ref. [10], a two-level data selector was proposed to solve the problem. The first level had three 2 : 1 MUX, and the second level an 8 : 1 MUX. The first stage TS56 chooses XIN [5:3] as the input, and the second stage XIN[2:0]. The two stages have pulse widths of 56t0 and 7t0, respectively. Finally, 64 proportional time-series signals are generated by combining eight different widths of the 8 : 1 MUX input. The operation waveform is illustrated in Fig. 9(c). The 64 different pulse widths can act on the charging time of the BL through the constant current source such that the BL has 64 types of precharging voltage corresponding to the input. Finally, this circuit can achieve up to six bits of DAC input.

Fig. 10. (Color online) Redundant reference column technology.

As shown in Fig. 9(d), the DAC circuit, used for pulse height modulation, is composed of a binary weight current source and a copy unit[15,16]. In a current source circuit, a fixed voltageVBISis applied to the gate of transistors with different width-length ratios. It produces different proportions of current according to the input data and then passes it through the diode-connected MA,R, generating a weighted voltage at the WL to realize BL discharge proportionally. Similarly,Ref. [65] used a current-type DAC to realize different pulse heights and applied it to the BL, thereby realizing multibit input.

The DAC precisely controls the proportional discharge of transistors. However, the transistor itself is a nonlinear device,so the discharge rate cannot be controlled proportionally.Thus, both techniques encounter the problem of nonlinear calculation results. Solving this is particularly important for the SRAM-based CIM.

3.3.Redundant reference column circuit

The in-memory Boolean logic, CAM operation, and MAC require multiple reference voltages. In practice, multiple reference voltages cannot be simultaneously connected due to the limited external pins of the chip. To address this, multiple reference voltages must be implemented in an array. A common technique for generating the required reference voltages in an array is by the redundant reference column circuit.

As shown in the orange rectangle in Fig. 10[5], the BL and BLB of the redundant reference column are shorted together.Therefore, the parasitic capacitance of the redundant reference column is twice that of the main array. The BL voltage of the redundant reference column is reduced by half relative to the BL voltage of the main array, generating the desired reference voltage. The redundant column with buffers generates the required reference voltages, as well as tracks the PVT variations in the memory array, thereby increasing the sensing margin. Siet al.[1,2]proposed a dynamic inputaware reference generation scheme to generate an appropriate reference for the binary dot-product accumulation mode.Two redundant columns were used as the reference column.The BLs of the reference columns were selectively connected through switches to generate different reference voltages. Generating multiple reference voltages in a memory array increased the functionality and enhanced the accuracy of the entire system.

3.4.Digital auxiliary computing circuit

Although most of the repeated operation functions are completed in the analog domain, the accumulation of the analog results is technically difficult. Digital domain accumulation is a good choice, and digital auxiliary circuits can significantly improve the computational accuracy of the system.

Fig. 11(a) illustrates a digital-aided technique for 2- and 3-bit multiplication. The Boolean logic “AND” and “NOR” functions are realized by an SA sensing the voltage of column CBL or CBLB[12,13]. Then, the addition operation is implemented by the Boolean logic. Finally, the trigger and data selector are used to accumulate the results of the addition operation to execute multiplication.

The digital circuit not only assists in the execution of multiplication but also the MAC, as shown in Fig. 11(b)[22,31,58].The bit-tree adder is used to obtain the cumulative sum of the BL quantization results. For an array withNnumbers to be accumulated, a log(N)-layer full adder is required to perform population count.

Digital calculations are highly precise. However, this method requires multiple cycles and has a relatively large area overhead and power consumption. The efficient use of digital circuits is a research direction in in-memory computing.

3.5.Analog auxiliary computing circuit

The analog domain auxiliary circuit has a lower calculation accuracy than its digital counterpart; however, it can achieve a higher computing ability with limited area and energy consumption. Kangetal.[35,36,45,50,66]proposed a signed multiplier in the analog domain. The timing diagram is illustrated in Fig. 12(a), and a schematic of the same is depicted in Fig. 12(b). First, the analog voltage corresponding to the 8-bit weighted data are shared with five capacitors of equal size throughϕdumpconnected to the multiplier. Then,ϕ2,0–ϕ2,3is activated by a 4-bit digital input XLSB. If the corresponding input data is 0, it is deactivated; otherwise, it will be activated. Finally,ϕ3,0–ϕ3,3is, in turn, activated to redistribute the charge, and the final voltage is proportional to the multiplication of the input XLSB and weight. The 8-bit input is realized through two operation cycles, and one cycle processes 4-bit data. The array is not used to complete the multiplication; hence, it does not require reconstruction, preserving its storage density and robustness.

4.Computational functions of the SRAM-based CIM

Because the internal cells of an SRAM array are repetitive,the operation in memory must be simple and repeatable. The existing SRAM-based CIM can be classified into two: pure digital CIM and mixed-signal CIM. The pure digital CIM mainly includes Boolean operation and CAM, and the mixed-signal CIM the processing of the Hamming distance, MAC, and SAD.

4.1.Digital SRAM-based CIM

4.1.1. Boolean logic (AND, OR, NAND, NOR, XNOR, XOR,and IMP)

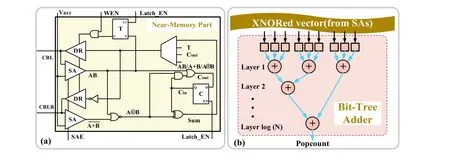
Fig. 11. (Color online) (a) In-/near-memory computing peripherals and (b) a bit-tree adder.

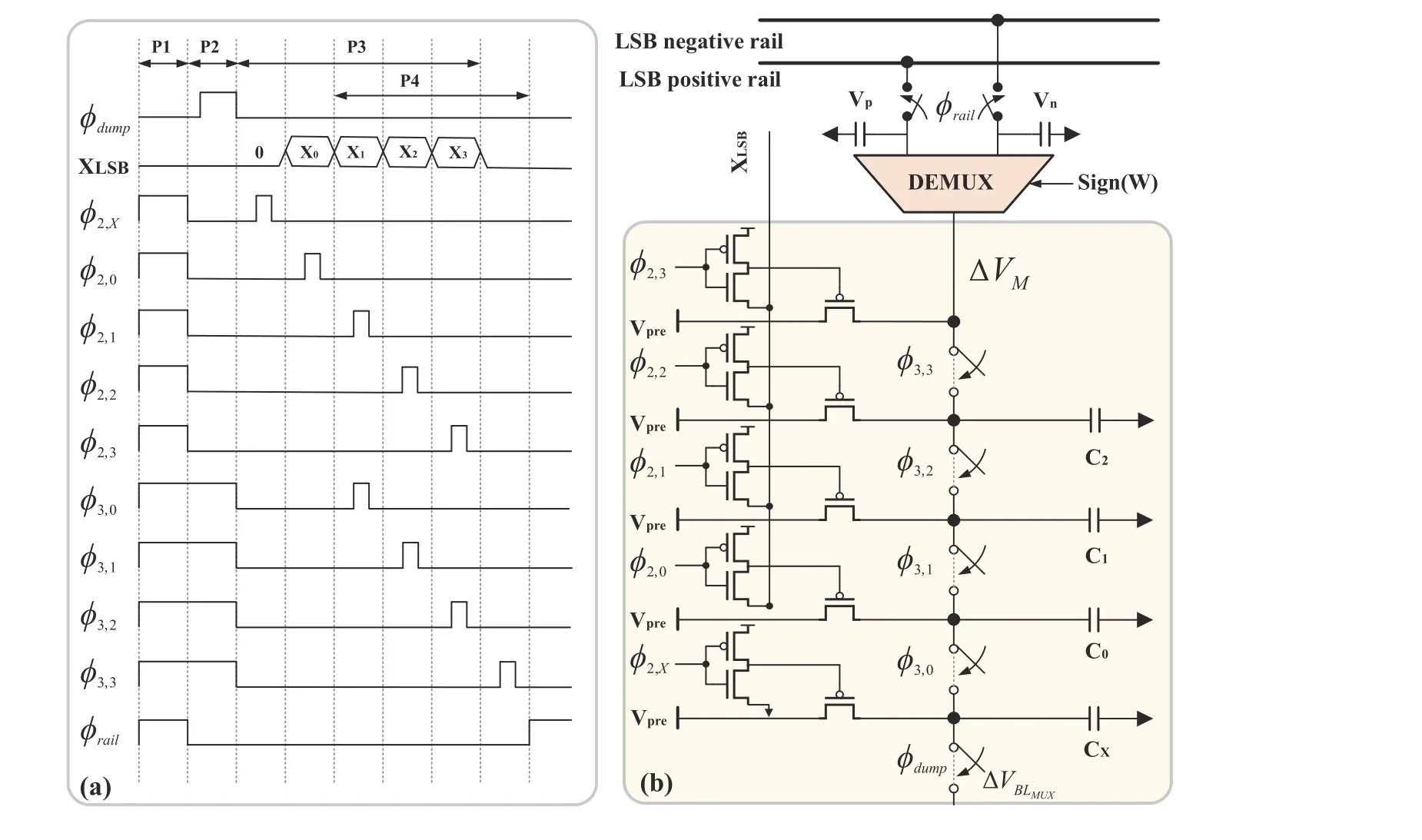
Fig. 12. (Color online) Signed 4-b × 8-b least significant bit (LSB) multiplier: (a) timing diagram and (b) circuit schematic.

Implementing the Boolean logic in memory is relatively simple and accurate because its operation is completed in the digital domain. Fig. 13(a) illustrates a basic construct for performing in-place bitwise logical operations using SRAM[19,20,22,24]. To realize the logic operations of A and B,the BL and BLB are first precharged to VDD. Then, the WL of the corresponding cell is turned on, and the two BLs are discharged according to the data stored. If AB = 11, BL will not discharge; if AB = 01/10, BL will discharge to a certain level; if AB = 00, BL will discharge to the maximum, as shown in Fig.13(b). The SA can realize different logic functions, such as AND and NOR, by setting different VREF values. Finally, XNOR can be realized by combining ‘AND’ and ‘NOR’ through the OR gate to implement the full Boolean logic. Fig. 13(c) shows the implication logic (IMP) and XOR logic[18]. In the CIM mode, SL1 is connected to the VDD supply, while SL2 is grounded, forming a voltage divider. RWL1 and RWL2 are initially grounded, and RDBL is precharged to Vpre (at 400 mV). The voltages of RWL1/ RWL2 represent the input data. If Q1 and Q2 store data ‘1’ and the input is ‘00/11’ (RWL1 = 0, RWL2 =0; RWL1 = 1, RWL2 = 1), RDBL remains Vpre; if the input is ‘01’(RWL1 = 0, RWL2 = 1), RDBL discharges to ground; and if the input is ‘10’ (RWL1 = 1, RWL2 = 0), RDBL charges to VDD. Finally, the results of IMP and XOR can be realized by using two skewed inverters to sense the RDBL voltage.

Most of the existing Boolean logics are realized by opening two rows of cells and sensing the BL voltage by setting the SA reference voltage[5,7,21,23−27]. Implementing multiple input logic operations in a single cycle and XNOR without additional combinational logic gates is challenging. Suranaet al.proposed a 12T dual port dual interlocked storage cell SRAM to implement the essential Boolean logic in a single cycle[23].Linet al. leveraged the three types of BLs of a traditional 8TSRAM to simultaneously realize four input logic operations[5].Zhanget al. proposed an 8T-SRAM with dual complementary access transistors[64]. It utilizes the threshold voltage of NMOS and PMOS, precharges the BL voltage to 0.5 VDD, and finally configures different reference voltages to realize the Boolean logic. In addition, a composite logic operation can be realized without additional combinational logic. The existing methods add additional cycles to store results in other cells[18];however, it decreases the speed and storage density of the system. The future direction of in-memory Boolean logic is to effectively store the calculated results.

4.1.2. Content addressable memory (CAM)

Fig. 13. (Color online) Boolean operation: (a) Boolean logical operations using an SRAM array, (b) histogram of AND and NOR operation voltages,and (c) schematic of the 8T-SRAM for implementing the IMP and XOR operations.

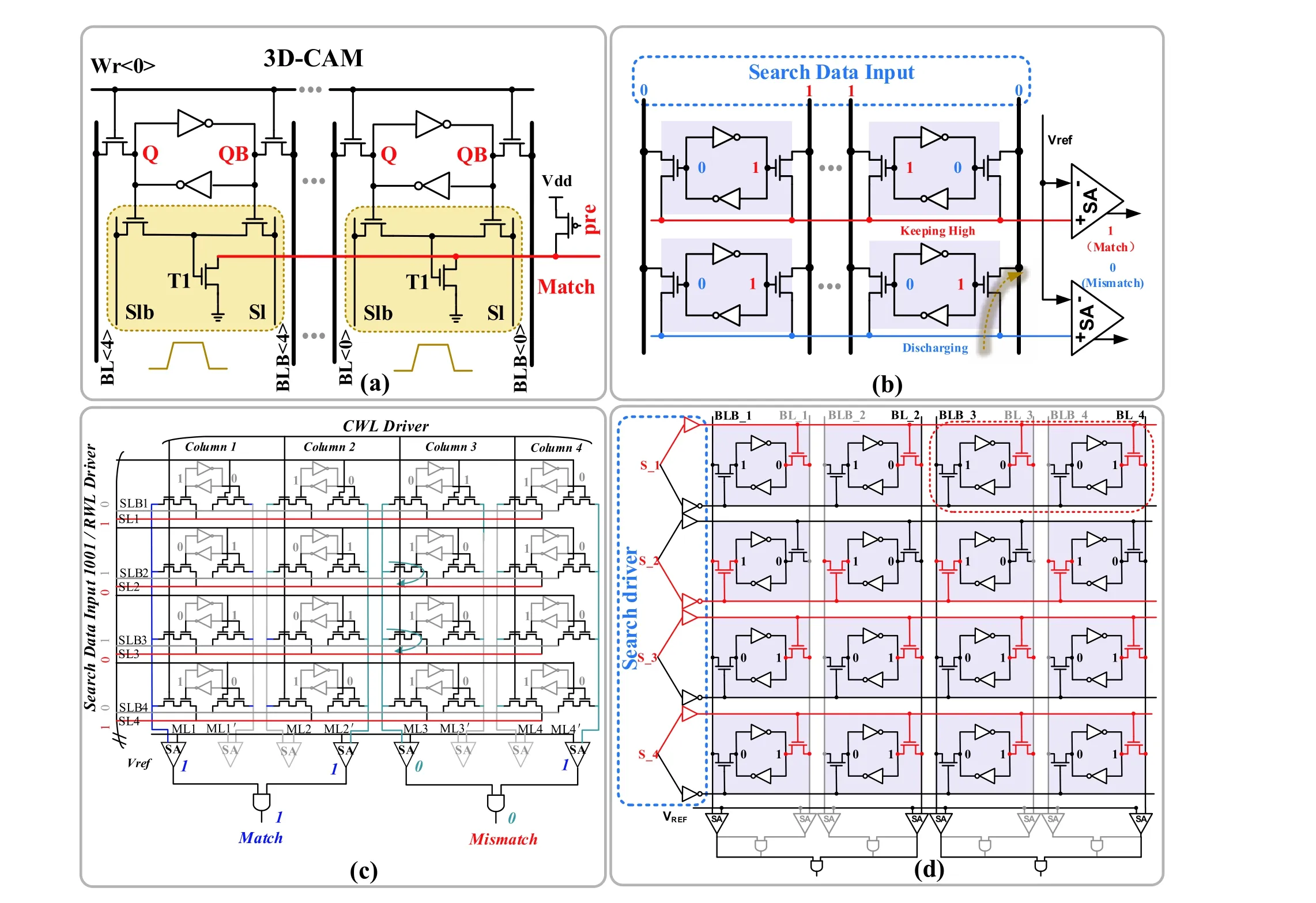
Fig. 14. (Color online) Column-wise BCAM: (a) search example in 3D-CAM and (b) 4+2T. Row-wise TCAM: (c) organization based on 10T and (d) organization based on 6T.

The CAM is a special type of memory that can automatically compare input data with all the data stored in the array simultaneously to determine whether the input data matches the data in the array. The realization of CAM in SRAM can reduce data transmission and avoid a large amount of energy consumption. The CAM operation can be divided into binary CAM (BCAM) and fault-tolerant ternary CAM (TCAM). In addition, there are two different search modes, including rowwise search and column-wise search. The row-wise search is defined as the cases where the input searching data are represented by lines connected by rows. Similarly, the column-wise search is defined as the cases where the input searching data are represented by lines connected by columns. In Figs. 14,(a) and (b) are the column-wise BCAM operations, and (c) and(d) are the row-wise TCAM operations. Srinivasaet al.[6]used the array structure shown in Fig. 14(a) to execute a columnwise BCAM operation. In the CAM operation, the data to be searched are stored in an array, and the search data are represented by the voltage values of the source line (Sl) and Slb. If the data to be searched matches the search data, the precharged match line is considered not-discharged and vice versa. To save area during CAM operations, Donget al.[20]pro-posed a 4 + 2TSRAM. The data to be searched is also stored in an array, and the search data is represented by the BL voltage. The SA is used to capture the voltage value of the matching line to obtain the result, as shown in Fig. 14(b). Because the two studies represent the search data by the BL voltage, all the memory units are column-wise addressable.

Table 2. Summary of chip parameters and performance of in-memory Boolean logic and CAM

The difference between TCAM and BCAM is that the former has a do-not-care state. Two cells are used to represent one data point owing to the presence of three states in the TCAM. The three states, 0/1/X (where X is an independent state, a do-not-care state), are represented by 00/11/01, respectively, whose implementation for column-wise search is shown in Fig. 14(c). The data to be searched is represented by two adjacent cells in a row, and the search data by the SL/SLB voltage. The intermediate ML1’/ML2 of two adjacent columns are shielded, and the matching result is determined by whether the other two MLs are discharged[11]. In addition,to match the characteristics of the data stored in rows in an SRAM, this work used 10T-SRAM to simultaneously implement CAM in the row and column dimensions. In order to save area, Jelokaet al. used standard 6T cell achieving TCAM operations, as shown in Fig. 14(d)[19], where the search data are represented by WLs voltage and the nodes in two adjacent cells in a row represent the searched data. Similarly, the search results are obtained by SA sensing the BLs voltage.However, unlike Refs. [11, 19 ], Ref. [29] used the virtual ground wire technique as the sensing mechanism. The virtual and actual grounds are connected via a diode, and the SA detects the voltage of the virtual ground, obtaining the ternary addressing result.

Linet al.[5]and Chenet al.[28]utilized the 8T unit to complete the CAM operation. The difference between the two studies is that the former used the BL as the data search line,whereas the latter used the WL. Ref. [67] used the CAM auxiliary circuit techniques to improve the operational speed of the system under ultra-low voltage. In Ref. [68], the CAM function was realized by combining two 6T cells with two additional control transistors.

In Table 2, the performances of several CIM Boolean logics and CAM are compared and the different search modes are presented. Most studies have implemented both Boolean operations and CAM by modifying standard cells, indicating the compatibility of these two functions. However, few have achieved CAM function in two directions simultaneously. Currently, in-memory Boolean logic is realized at the cost of reduced parallelism as opposed to its analog counterpart. Therefore, improving the parallelism for Boolean logic and using it to achieve sophisticated calculations in memory will be a direction for research.

4.2.Mixed-signal SRAM-based CIM

The mixed-signal SRAM-based CIM is primarily categorized into two types: 1) single-bit operation, including binary and ternary dot products, and Hamming distance, and 2) multibit operation, including multibit multiplication and SAD.

4.2.1. Single-bit operation0

A. Binary dot product

The multiplication operation of a single bit is also a dotproduct operation. As mentioned previously, there are two subtypes of this operation: binary and ternary dot products.Chiuet al. executed (1,0) × (1,0) and (1,0) × (+1, -1) dotproduct operations with standard 6T cells[33]. The input is represented by the WL voltage. The weight is represented by 6T storage data. The truth table is used to summarize the combinations of different inputs and weights, as shown in Fig. 15(a).The binary dot product results are represented by the voltage difference between BL and BLB. The BL voltage changes according to the result of the multiplication of the input and weight. Sunet al. proposed a dedicated 8T-SRAM cell for the parallel computing of a binary dot product[30,69](Fig. 15(b)). There are two complementary WLs (i.e., WL and WLB) and two pairs of pass gates (PGs) to achieve the operation function. The first pair of PGs is controlled by the WL and connects Q and QB to BLB and BL, respectively, while the second pair of PGs is controlled by WLB and connects Q and QB to BL and BLB, respectively. The proposed 8T-SRAM always contains a non-zero voltage difference between BL and BLB, which represents the results of the binary-weight multiplication operations. The truth table in Fig. 15(b) reveals the combination of different inputs and weights, and the corresponding changes in the BL discharge current (Δi) and voltage(Δv) caused. In addition, according to the input neuron vector, a WL switch matrix is used to simultaneously activate multiple WLs. The discharge current from several bitcells in the same column decreases the voltage of the BL (BL or BLB).Thus, the voltage difference between BL and BLB can be used to determine the weighted sum.

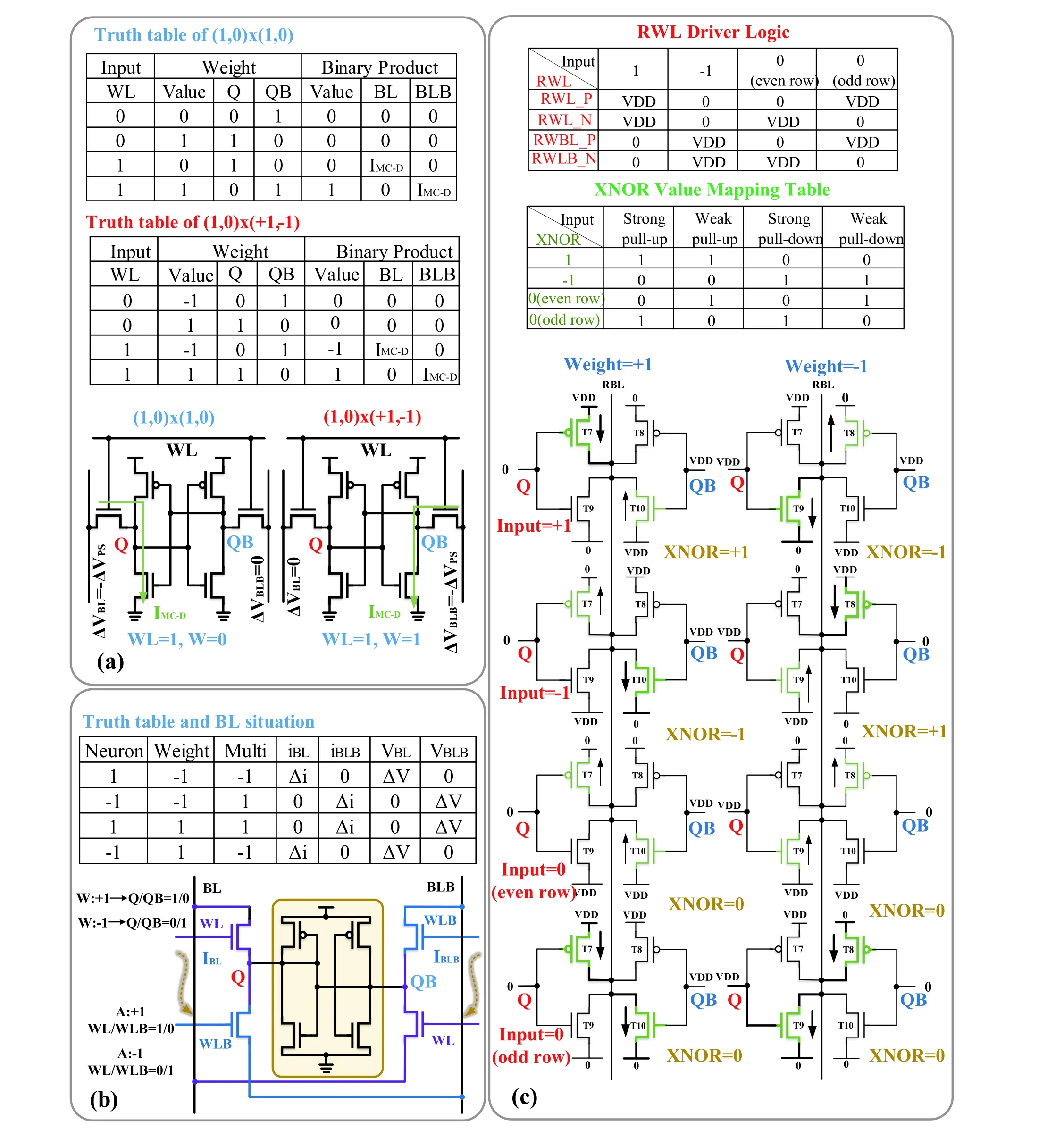
Fig. 15. (Color online) Schematic and truth table of the binary dot product: (a) 6T-SRAM binary dot product and (b) 8T-SRAM binary dot product.(c) Ternary dot product: operation of ternary multiplication and XNOR value mapping table.

The cumulative result of the above study is on the BL;therefore, the operation should be performed by columns.However, in the traditional SRAM storage mode, data are stored row-wise. The CIM mode conflicts with the storage mode, which reduces the operation efficiency. To address this problem, Agrawalet al. used a 10T SRAM to perform a binary line dot product, and the results were reflected on the horizontal source lines[9], conforming to the traditional SRAM storage mode. However, the storage density is reduced by the introduction of additional transistors in the basic cell.

Fig. 16. (Color online) Row of 9T SRAM cells for calculating the Hamming distance.

B. Ternary dot product

Yinet al. achieved a ternary dot product[17](Fig. 15(c)).For the XNOR operation if the result is +1, PMOS provides a strong pull-up, and NMOS a weak pull-up on the RBL. If the result equals –1, then NMOS provides a strong pull-down and PMOS a weak pull-down. A resistor divider is formed for cells on the same column, with the RBL as the output. The voltage on the RBL represents the accumulation of the XNOR results in that column. For XNOR with ternary activations input (+1,0, or –1) and binary weights, an additional case of ‘0’ input must be considered. As shown in Fig. 15(c), if ‘0’ input is in the even row, the PMOS provides a weak pull-down and NMOS a weak pull-up on the RBL. If ‘0’ input is in the odd row, the PMOS provides a strong pull-up and NMOS a strong pull-down on the RBL. Assuming there is a sufficiently large number of inputs, half of the inputs will be in the even row and the other half in the odd row. Thus, the cumulative increase and decrease in the RBL voltage are 0. The result of the ternary multiplication is summarized in the truth table in Fig. 15(c).

As the input and weight of the dot-product operation are in single bits, no additional auxiliary circuits are required to process the weight, and the quantization of the operation results is simplified. The dot-product operation can be applied to the binary neural network (BNN) algorithm, where the inputs can be restricted to either +1/–1 or 0/1. When the inputs are restricted to 0 or 1, it has a 0.03% loss of accuracy compared with +1/–1 input, which is tested in the MNIST dataset[1]. However, because these studies used the analog voltage of BLs to reflect the operation results, they could not obtain results that are as accurate as the digital CIM.

C. Hamming distance

The Hamming distance algorithm is widely used in signal processing and pattern recognition. The Hamming distance between any two vectors of the same length is defined as the number of corresponding bits with different values.The principle of Hamming distance is that two bytes of the same length are bitwise XNOR and these XNOR results are then accumulated. For example, the Hamming distance from 1101 to 0111 is 2. Because this algorithm also requires high data access, it consumes a significant amount of energy when used in the traditional architecture.

Aliet al. proposed a 9T SRAM to calculate the Hamming distance[8], as illustrated in Fig. 16. One of the vectors is stored in the memory array, while the other vector is used to drive the RBL/RBLB. For example, if the input vector is ‘1’, the RBL is connected to VDD, and the RBLB to GND. If the data in one cell match the input, SL is connected to VDD through M1,n.If it mismatches the input, the SL is connected to GND through M2,n. Hence, this circuit forms a voltage divider at the SL. Finally, the results of the Hamming distance accumulate on the SL.

Unlike the row-wise Hamming distance operations, Kanget al. proposed a column-wise Hamming-distance macro based on a 6T SRAM array[70]. In this design, two inputs are stored in two different rows in the same column. Then, the logic operation between the two inputs is executed by the SA.The final Hamming distance value is obtained by combining and accumulating the outputs of the SA. Because the result of the study is represented by BLs connected by columns, the Hamming distance is calculated column-wise.

In CIM, most of the results are reflected on BLs of column-wise connection. Therefore, vertical data storage is generally required, increasing the implementation complexity for the SRAM writing mode. For example, Jelokaet al. proposed a strategy of column-wise write[19]. It writes 1 in the first cycle and 0 in the latter cycle, which decreases the written data throughput and writing speed. In addition, as a basic and important operation, matrix transposition is generally realized by data reading, moving, and writing back in a complicated operation with high power consumption. Thus, it will be a research direction to realize Hamming distance operation in both the row and column directions.

4.2.2. Multibit operation

Unlike single-bit operations wherein the operands are limited to only 0, –1, and 1, multibit operations can obtain more precise in-memory computations, which meets the requirements of various AI algorithms. There are two main categories of multibit operations: 1) multibit multiplication and 2)SAD.

A. Multibit multiplication

The key to multibit multiplication is the weighting strategy. The weighting strategies include pulse width[10,35,36,39,40,45,50,56,64,66,71], pulse height[10,15,16,44,56], number of pulses[37,38], width-to-length ratio of transistors[3,32,42,43,62], capacitor array weighting[37,38,62,63,72,73], and precharge time weighting[44]. The specific implementation strategy of the capacitor array weighting technology is introduced in Section 3. The multibit multiplication is reviewed from the following five aspects:

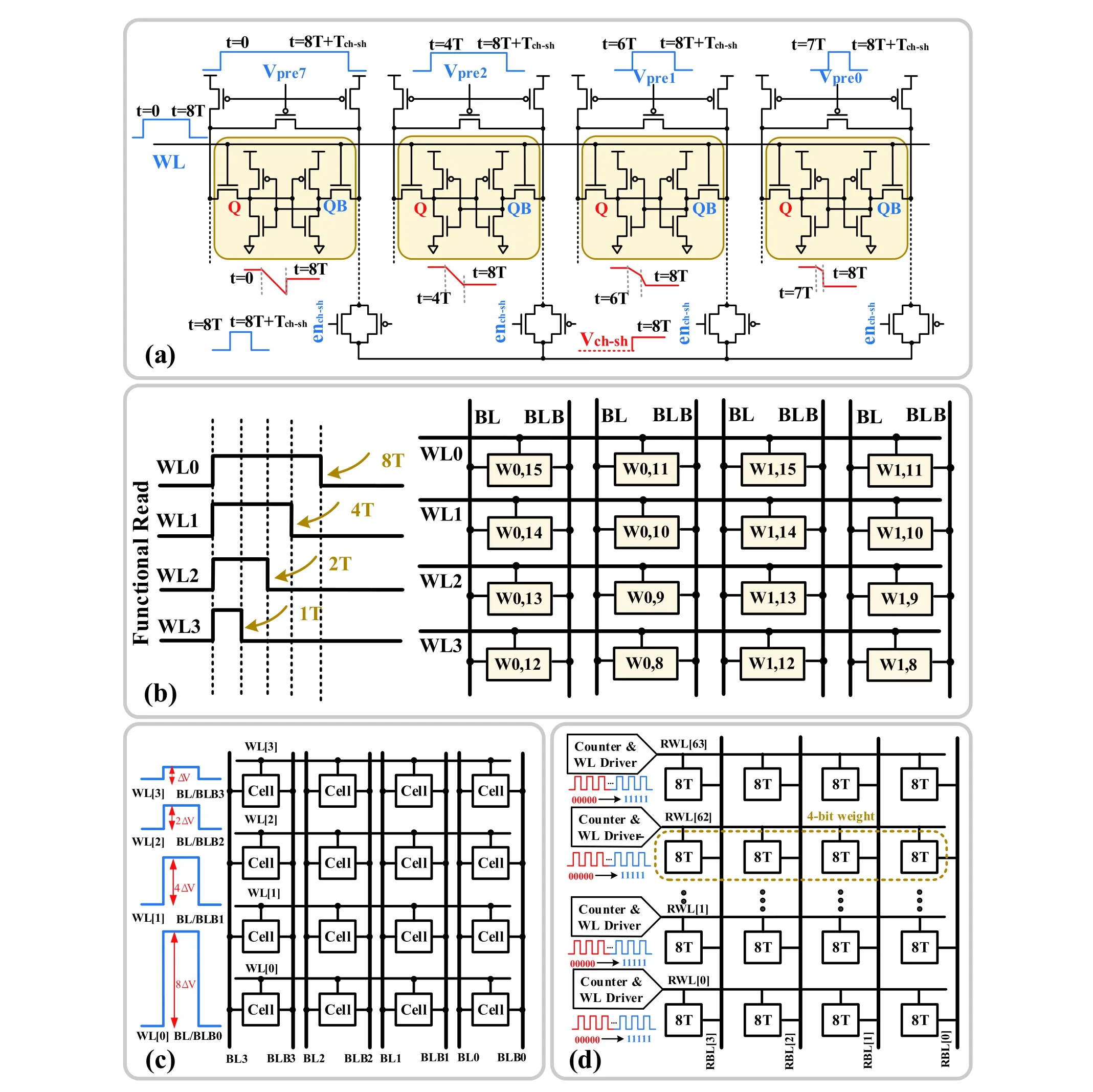
Fig. 17. (Color online) (a) Precharge weighting technology, (b) pulse width weighting, (c) pulse height weighting, and (d) pulse number weighting.

1) Precharge time weighting

Fig. 17 illustrates various pulse-based weighting techniques. Aliet al.[44]used the standard 6T and controlled the BL precharge time to achieve multibit multiplication operations (Fig. 17(a)). In Aliet al. study, the 4-bit weight is stored within the adjacent 6T SRAM cells in a row. The 4-bit input is reflected in the WL. When performing a 4-bit multiplication operation, the pulse width of the WL is 8T and its amplitude is dependent on the input. The closing times of the precharge circuit from the first to last columns are [0, 8T+Tch-sh], [4T,8T+Tch-sh], [6T, 8T+Tch-sh], and [7T, 8T+Tch-sh], respectively,where Tch-sh is the merging period. Because the opening time of the WL is 8T, the discharge times of the BL from the first to last columns are approximately 8T, 4T, 2T, and T, respectively.

2) Pulse-width-weighting

During the SRAM read operation, when the BL voltage is maintained within a certain range, its discharge voltage is proportional to the WL turn-on time; that is, the decrease of the BL voltage can be controlled by controlling the opening time of the WL. Therefore, by doubling the opening width of each WL, a proportional increase in the BL voltage change can be obtained. Sujanet al.[45,66]proposed a functional read technology based on pulse-width modulation strategy for 4b weighting (Fig. 17(b)). In this work, the turn-on time of WL0-WL3 can be modulated to 8 : 4 : 2 : 1 to execute the 4b-weighted multiplication operation.

3) Pulse height weighting

Fig. 18. (Color online) (a) 8T-SRAM memory array for computing dot products with 4-bit weight precision and (b) Twin-8T cell.

As shown in Fig. 17(c), different pulse heights can be applied to the WL or BL. Zhanget al.[15,16]used the WL ADC technology to implement a machine learning (ML) classifier. Different voltages applied to the WL represent different weights,and the access transistor is considered to have discharged approximately linearly according to the WL voltage, thereby realizing multibit multiplication. Biswaset al.[10,56]realized the weighting of the dot-product sum based on a 10T SRAM array. They executed the multibit multiplication by charging the BL to different voltage values with different pulse heights.

4) Weighting strategy based on the number of pulses

Donget al.[37,38]designed a 7-nm FinFET CIM chip for ML that uses a pulse number modulation circuit (Fig. 17(d)). The 4-bit input is represented by the number of read word-line(RWL) pulses. These pulses are generated by a counter according to the value of the input data and are applied to the RWL to turn on the corresponding cells. The discharge amount of the BL is proportional to the number of times the RWL is turned on, thereby executing multibit multiplication.

5) Weighting strategy based on the transistor width–length ratio

As depicted in Fig. 18(a), in the 8T array, the sizes of the read access transistors in different columns are adjusted in proportion to the weights of the input data[3]. The width–length ratios of M1 and M2 in the first, second, third, and fourth columns are 8 (W/LM1,2 = 8) and 4 : 2 : 1, respectively. Therefore, the sum of the multiple bits multiplied by one bit can be obtained. The study combines the BL discharge currents of the four columns and converts the current value into a voltage value through an operational amplifier, which is ultimately quantified by the ADC. Similarly, Siet al. proposed a twin-8T structure based on the traditional 8T[32]and adjusted the width–length ratio of one group of reading transistors to twice that of the other group to achieve 2b input weighting(Fig. 18(b)). Suetal.[43,62]proposed a transposable arithmetic cell structure and quantified its internal weighting by the width–length ratio of the transistors, achieving simultaneous bidirectional calculations.

Different designs have tradeoffs among time cost, implementation difficulty, linearity, area cost, and process. 1) Precharge time weighting: When the precharge and the word line are turned on simultaneously, there will be a relatively large current which will increase power consumption. 2)Pulse-width-weighting: Its operation is relatively simple.However, when the input bits increase, the corresponding pulse width will increase proportionally; thus, the time increases exponentially, resulting in a significant decrease in calculation speed. Moreover, when the bit line voltage is relatively low, linearity will also be a problem. 3) Pulse height weighting: TheV–Icharacteristic of metal–oxide–semiconductor (MOS) devices is that the current between the source and drain increases proportionally to the square of the gate voltage. Therefore, unlike 2), the pulse height cannot be increased proportionally to ensure proportional discharge of the bit line, so it is difficult to set the pulse height. In addition, the linearity is relatively poor compared with 2). 4) Pulse number weighting: As this design controls the discharge numbers of the access transistor, it is basically consistent with 2);thus, there will be similar problems. 5) Weighting based /on transistor width–length ratio: The proportional discharge of bit line can be realized by adjusting the width–length ratio of transistors. However, increasing the size of the transistor will also increase the area overhead, bring difficulties to the layout process and cause mismatch due to the oversized array ratio. The above weighting design methods are all a tradeoff between the octagonal rules of circuit design.

B. Sum of absolute difference (SAD)

Kanget al. executed a SAD operation based on a 6T SRAM array without sacrificing storage density[35,50]. In the SAD, the template patternPis stored with a polarity opposite to that ofD. BothPandDare stored in four adjacent cells in a column, as shown in Fig. 19(a). The decimal data can be read out on the BL through multirow read technology with WL pulse modulation. For example, if the data stored in four consecutive cells in a column ared= ‘1111’, the decimal number isD= 15. When reading the data with four weighted pulse WLs (WL0–WL3), the BL voltage decreases by 15Δv, as shown in Fig. 19(b). BecausePandDare stored in the array in the opposite manner, the AD operation results can be obtained by comparing the voltages of the two BLs. These outputs are summed via a capacitive network using a chargetransfer mechanism to generate the SAD.

Table 3 summarizes the performances of existing single and multibit operations. The number of input and output bits reflect the performance of the operation. However, the difficulty lies in improving the effective number of bits (ENOB) of the final output result without using a high ENOB ADC. This is because the overhead of a high ENOB ADC is unacceptable as it deviates from the original intention of low-overhead in-memory computing.

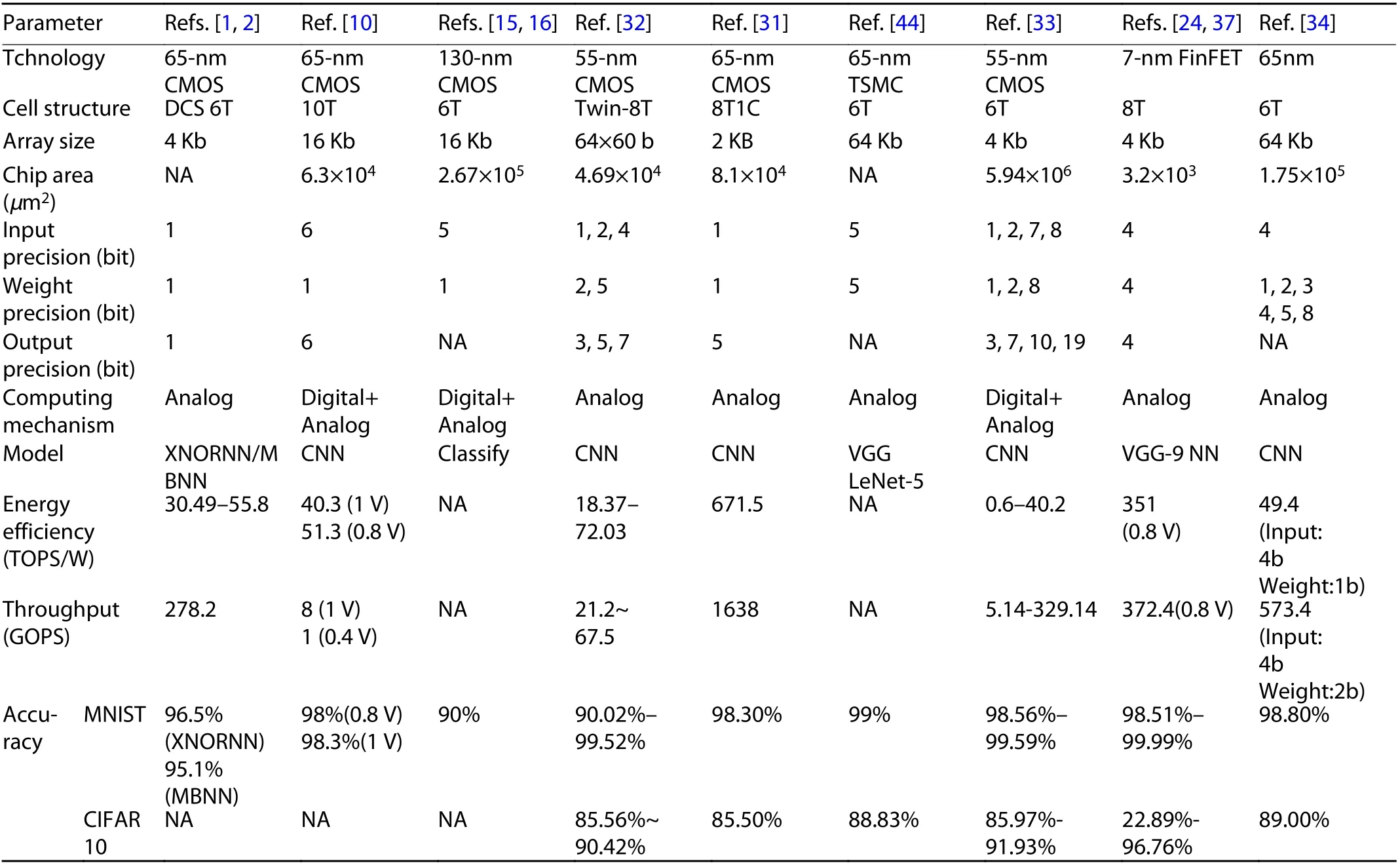
Table 3. Summary of chip parameters and performance of single- and multibit operations.

Fig. 19. (Color online) (a) Schematic of SAD circuit and (b) sequence diagram.

5.Application scenarios for CIM

The computing functions realizable by CIM have been widely used in various fields, including image and voice recognition, which require data exchange between encryption and decryption algorithms for data security. In this section, the application scenarios of CIM, including CNN, AES, k-NN, and classifier algorithms, are introduced.

5.1.Application in CNNs

Inspired by biological neural networks, artificial neural networks are used in image processing and speech recognition.A deep neural network (DNN) contains at least two layers of nonlinear neural units connected via adjustable synaptic weights. These weights can be updated according to the input data to optimize the output. In 1990, a dedicated hybrid chip was developed for multilayer neural networks[74].However, owing to its lack of flexibility, it was eventually abandoned and replaced by general-purpose programmable chips, such as field programmable gate arrays and general-purpose graphics processors. The implementation of the DNN algorithm requires the transmission of massive volumes of data between the memory and the CPU, and the resulting delay and power consumption limit the further development of DNNs.

CNN algorithms evolved from DNN algorithms are fully applied in image processing. A CNN algorithm can be mapped onto multiple intercommunicating SRAM arrays, as illustrated in Fig. 20(a). Each layer of the CNN contains several repetitive MAC operations, and implementing these MACs in the traditional von Neumann architecture results in a large overhead. In CIM, the weights of the layer are stored in SRAM cells, and the input is represented by WLs or BLs. A large amount of data flowing between the processor and the memory is eliminated. The final accumulation results are often reflected in the BL voltage. Quantifying the analog voltage of the BL is key to the entire operation.

Fig. 20. (Color online) Implementation of (a) CNN and (b) AES on multiple SRAM arrays.

The weights and inputs of the CNN are usually multibit.However, to realize multibit operation in memory, it is necessary to change the cell structure or add auxiliary circuits.A twin-8T structure was proposed to realize 1b, 2b, and 4b inputs and 1b, 2b, and 5b weights, with an output of up to 7b[32]. The test accuracy of the system using the MNIST dataset was as high as 99.52%. To simplify circuit design, researchers have developed the BNN, with binary inputs and weights,i.e., “+1” or “–1.” In simple application scenarios, it has nearly the same accuracy as the traditional CNN algorithm[1,2]. Chihet al.[75]proposed another solution that uses all-digital CIM to execute MAC operations and has high energy efficiency and throughput. In order to reduce computational costs, Sieet al.[76]proposed a software and hardware co-design approach to design MARS. In this study, a SRAM-based CIM CNN accelerator that can utilize multiple SRAM CIM macros as processing units and support a sparse CNN was also proposed.With the proposed hardware-software codesigned method,MARS can reach over 700 and 400 FPS for CIFAR-10 and CIFAR-100, respectively. Although these studies have realized in-memory MAC, they could not execute the entire CNN process in memory. Therefore, the execution of the entire process in memory can be a possible research direction.

5.2.Application in encryption algorithms

With the development of AI, the amount of data that requires processing has surged and concerns about data security have increased. For example, the convolution kernels in the CNN algorithm and convolution step are obtained by training with a large volume of data. However, the entire weight is stored in the array and, therefore, can be easily read, causing data leakage. Encryption is crucial to big data. However,the power consumption and delay in implementing a set of encryption algorithms in the digital domain will limit the overall performance of the system; hence, researchers have proposed to implement these algorithms in memory.

Fig. 20(b) illustrates the process of the AES algorithm in four steps: byte replacement, row shift, column mixing, and round key addition. Byte replacement is used to replace the input plaintext with a look-up table and implement the first round of encryption. The row-shift operation shifts the transformed matrix by a certain rule. Column mixing is the XOR operation of the target and fixed matrices. Round key addition performs an iterative XOR between the data and the key matrix.

Fig. 21. (Color online) Application in the k-NN algorithm.

To implement the AES algorithm in an SRAM array, first,the plaintext matrix that needs to be encrypted is stored in the array. Then, the plaintext and key matrices are encrypted using a peripheral auxiliary circuit. The most repeated operation in the AES algorithm is the XOR operation; hence, implementing XOR in memory, storing the result, and continuing to perform the XOR operation with the input are key steps in the execution of the AES algorithm. Agrawalet al.[18]proposed a “read-calculation and storage” strategy based on the 8T SRAM, in which the obtained XOR result was stored in another row through a data selector at the end of each column,which implemented part of the iterative XOR operation for the AES. However, this strategy increases the area overhead of the storage array and consequently requires an additional empty row in the array to store the calculation results. Jaiswalet al. proposed interleaving WL (i-SRAM)[22]as the basic structure for embedding bitwise XOR computations in the SRAM arrays, which improved the throughput of AES algorithms by a factor of three. Huanget al. modified the 6T SRAM bitcell with dual WLs to implement XOR without compromising the parallel computation efficiency[46], which can protect the DNN model in CIM. These studies realized part of the operations in encryption, and the realization of the AES of the entire process in memory is a research direction.

5.3.Application in k-nearest neighbor (k-NN)algorithms

The k-NN algorithm is one of the simplest, most basic ML algorithms that can be used for both classification and regression. The concept of the algorithm is as follows: if most of the k-most similar samples in the feature space belong to a category, the sample also belongs to that category. There are two methods to measure the distance of two samples: the Euclidean distance and Manhattan distance.

In Fig. 21, I1 and I2 are the pixel values of the target and test images, respectively. First, the pixel values of the same position of the test and training images were subtracted, followed by calculating the absolute values and summing them. The sum represents the similarity between the test and target images. The smaller the value, the higher the similarity. The k-NN algorithm finds the first k images that are most similar to the target image. Kanget al. executed the SAD for application in the k-NN algorithm[35,50]. They used hand-written number recognition to test the accuracy of the algorithm on the MNIST dataset. The results showed that the CIM-based k-NN algorithm has a high recognition accuracy of 92%.

5.4.Application in classifier algorithms

Classification is a significantly important method of data mining. The concept of classification is to learn a classification function or construct a classification model (that is, what we usually call a classifier) on the basis of existing data.However, it is challenging to implement an energy-efficient classifier algorithm in resource-constrained devices. If the classifier algorithm can be realized with methods of CIM, the frequent data access will be greatly reduced.

As depicted in Fig. 22, high-precision boosted strong classifier can be realized by combining column-based weak classifier C1-M. However, there is a typical characteristic for calculations by column in CIM, which can be perfectly mapped into a column-based weak classifier. Zhanget al.[15,16]achieved an ML classifier based on the 6T cell. Because of the nonlinearity in column-wise CIM, the result of each column can only form a weak classifier. In memory, the boosted strong classifier can be obtained through adder or subtractor circuits that process the column-wise results which reduces the non-ideal characteristic of analog CIM. In addition, this design reduces the energy consumption by 113 times when using a standard training algorithm. Similarly, a random forest (RF) machine learning classifier can be enabled by a standard 6T SRAM in Ref. [40]. It achieved massively parallel processing thereby minimizing the memory fetches and reducing energy-delay product (EDP).

6.Challenges and prospects

With the rapid development of AI, requirements for computing power have become stringent. The CIM architecture has ushered in unprecedented development opportunities.All CIM strategies make a compromise among bandwidth,delay, area overhead, energy consumption, and accuracy. The following is an analysis of several typical problems in the CIM architecture.

6.1.Read-disturb issue

In CIM, it is often necessary to access multiple rows for simultaneous computation to increase the throughput of data processing. However, turning on multiple rows synchronously connects the storage node directly to the BL, which will cause data to be flipped during the reading process. Therefore, this strategy resulted in an error in the final calculation result; even worse, it destroys the stored data. As shown in Fig. 23, when the BL voltage drops decreases significantly and reaches the write margin, the cell storing ‘1’ will be mistakenly written to ‘0’. To address this issue, Kanget al.[35]reduced the discharge speed of a BL by reducing the turn-on voltage of the WL. When the WL voltage is reduced to a certain extent, the full swing BL voltage can be achieved when multiple rows are opened simultaneously. Researchers have suggested using read–write decoupling cells to achieve CIM operations, such as 8T[3,5,18,28,37,38,65,77,78]and 10T[9−11,56,57],which can also obtain the full RBL voltage swing (from VDD to ground). However, the bitcell adds transistors at the expense of the storage density of the array.

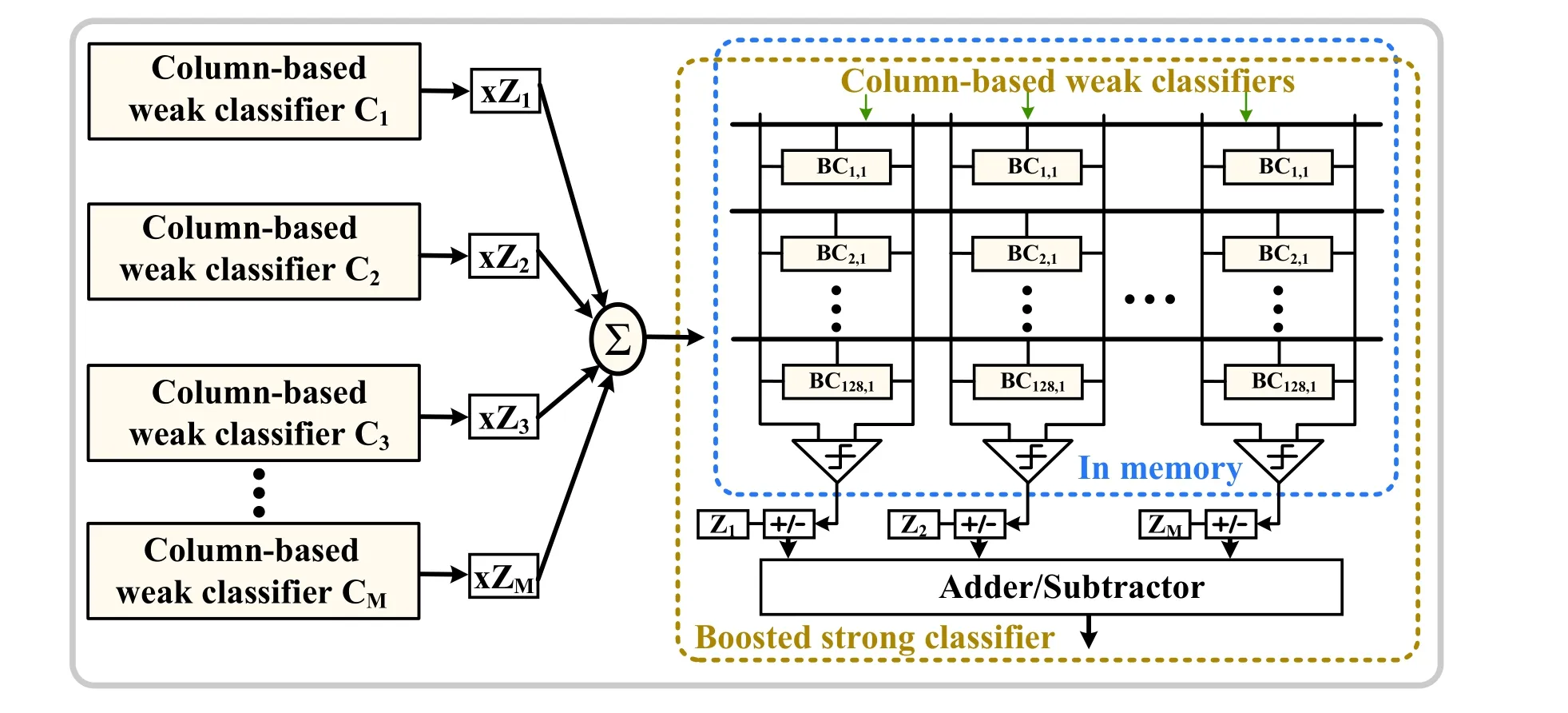
Fig. 22. (Color online) Application in classifier algorithms.

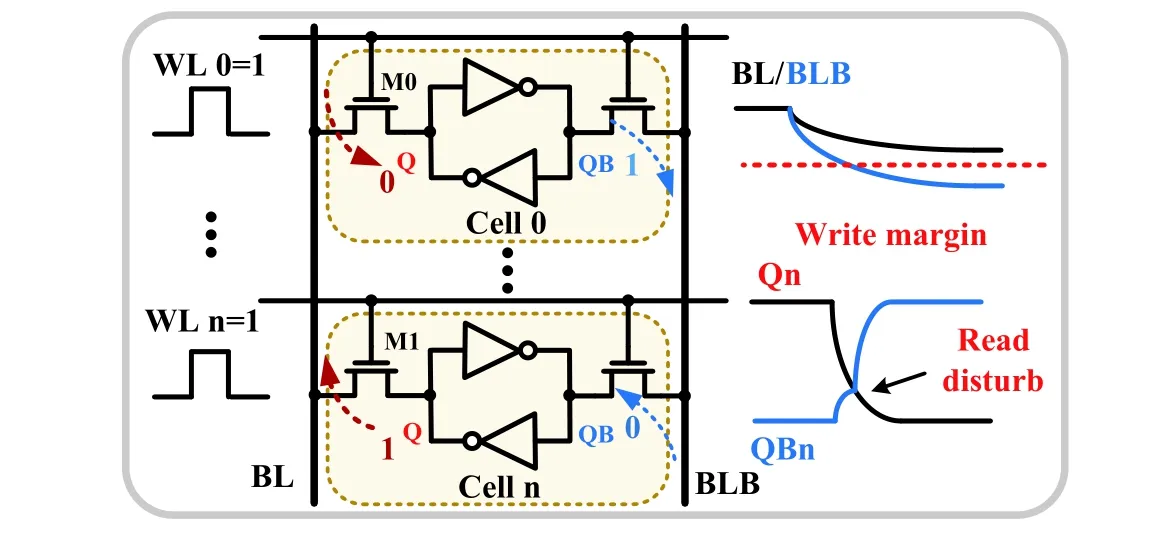
Fig. 23. (Color online) Read disturb issue.

6.2.Linearity and consistency problems in the SRAMbased CIM

The demerit of the SRAM-based CIM is the problem of preserving linearity and consistency, which directly determines the final calculation accuracy. In Fig. 24(a), only one row is activated at a time under the basic SRAM read operation, and the voltage difference between BL and BLB is detected by the SA to achieve a full swing output. In contrast, in Fig. 24(b), four rows of WLs are activated simultaneously to realize the calculation function, and the pulse widths of the WLs are 8T, 4T, 2T, and 1T. For example, if the input on the WL is‘1000’, the WL with an 8T width is activated. Ideally, the BL should reduce by 8∆v; however, in practice, it may only reduce by 5∆v, leading to erroneous calculations. Moreover,the asynchronization of the pulse width caused by latency and the imbalance of pulse width on each WL can cause a nonlinear BL discharge. In Fig. 24(c), the SRAM array is assumed to store identical data in each column, and the discharge is assumed to be 6∆vin the column closest to the pulse-width generator. Given the pulse-width distortion, the farther the column from the pulse-width generator, the smaller the discharge. For instance, the last column may only be discharged by 2∆v. Therefore, the linearity and consistency problems will affect the calculation results in a multiline read structure[35,45,66].

To address these problems, Linet al.[79,80]proposed a cascode current mirror (CCM) peripheral circuit and applied it to the bottom of each BL. The CCM clamps the BL voltage and proportionally duplicates the BL current in the additional capacitor, increasing the calculation linearity. In addition,they also proposed a double WL structure to reduce the pulse-width delay on the WL and increase the consistency of circuit calculations. They demonstrated the ability of the CCM circuit to reduce the integer nonlinearity by approximately 70% at 0.8 V supply and improve the computational consistency by 56.84% at 0.9 V supply.

6.3.Challenge of the array size under the CIM architecture

To increase the data throughput, the array size of the storage is often expanded; however, a series of factors limit the expansion. For example, to achieve specific functions, researchers introduced capacitors in each storage unit[31,58,60,61]. Although the introduction of capacitors increases the linearity of calculations, it also increases the power consumption and latency of the system.

Researchers including Jiang have proposed the C3SRAM(capacitive-coupling computing) structure to execute singlebit multiplication[31,58]. Because the cell uses a capacitor, the calculation result is ideally linear. However, each C3SRAM cell has a capacitor coupled with an RBL. Thus, 256 cells in a column are equivalent to 256 internal capacitors in that column, leading to a capacitance surge in the RBL.

The storage and computing architecture based on the 8T1C structure proposed by Jiaet al. also uses capacitors inside cells[60,61]. The BL capacitance has a similar cumulative effect as C3SRAM’s array; therefore, the overall array size is limited. Surplus capacitors in the array increase the precharge time and reduce the computational speed of the entire system.

Yinet al. designed an XNOR-SRAM cell for ternary multiplication[17], and the result is represented by the activation of the transistor. If the transistor is turned on, the result is equivalent to a resistor Ron. This design has 256 XNOR-SRAM cells in one column. During operation, 512 transistors are turned on,which is equivalent to 512 Ron connected in parallel on the BL, which causes the resistance on the BL to be insignificant,producing a large current and increasing the system’s power consumption.

Fig. 24. (Color online) (a) Single row activation during normal SRAM read operation, (b) multirow read and nonlinearity during CIM, and (c) inconsistent CIM calculation.

6.4.Area overhead and energy efficiency challenges of peripheral circuits

The architecture based on CIM requires several peripheral auxiliary circuits to perform additional computing functions. For example, when implementing logic operations in digital functions, two SAs are required on each BL to distinguish different inputs. When performing multiplication and accumulation in analog operations, the calculation results are reflected on the BL with an analog voltage. Therefore, peripheral auxiliary circuits are also needed to quantify these voltage values. The use of multiple high-precision ADCs for the quantification greatly increases the proportion of peripheral circuits.In addition, multibit input modules, such as multi-pulse width or pulse-height-generation circuits, occupy a large part of the area.

Yinet al.[17]designed a shared ADC with 64 columns,quantized it 64 times through a data selector, and added a fault-tolerant algorithm to further reduce the requirement of quantization and the overhead of the peripheral circuits. Kimet al.[81]used low-bit ADCs to achieve ResNet-style BNN algorithms via aggressive partial sum quantization and inputsplitting combined with retraining. The area overhead is reduced due to the use of low-bit ADC. Maintaining the proportion of peripheral circuits within an acceptable range comes with the loss of the accuracy of the final output digits. Interestingly, the complexity of the auxiliary circuit to achieve more complex calculations cannot be dismissed in the CIM systemlevel design.

In the future, peripheral circuits may be stacked in 3D to form a pool of peripheral circuit resources shared by CIM arrays. In addition, the use of peripheral circuits can be greatly reduced by time-division multiplexing, which further reduces the area of the SRAM-based CIM architecture.

6.5.Research prospect

6.5.1. More efficient mapping from common operators set to actual circuits set

In CIM, it is necessary to design various circuits to realize operations of the algorithm. The same operator can be realized by several circuits. In contrast, one circuit can also be used by multiple operators. Therefore, the problem of selection of the circuits set and effectively mapping the common operator set to it must be studied. As shown in Fig. 25, this problem can be studied from three aspects.

1) Refining and merging common operator sets. First, an initial set of common operatorsϕ(such as multiplication,SAD, addition and subtraction, and MAC) is extracted according to multiple factors, including requirements of AI algorithms, and computational complexity and efficiency. Then,part of the operators must be split based on the initial setϕ,which will facilitate the further integration of some operators and circuit implementation. For example, the SAD can be split into difference, absolute values, and addition operators.

2) Exploring the appropriate circuit sets. The design process of the circuit set must consider, for example, the coverage of the circuit set, its redundancy, the accuracy of the calculation, the cost of the circuit area, and circuit latency and power consumption. The circuits set can be subdivided by the computational complexity and data requirements. On this basis, a unified interface is designed for the circuit module, which is convenient for the upper architecture to organize and implement.

3) Designing word-column/row-block hierarchical sharing architecture. Flexible and configurable hierarchical architecture is key to realizing mapping from a common operator set to a circuit set. The memory array can be divided into a word-column/row-block three-tier system. The lowest layer is the word-level memory computing layer, which has the tightest memory computing coupling and requires the lowest area cost and power among all the layers. It can directly read and write the data of a single word, transmit it rapidly, and perform lightweight operations. The implementation of simple operators in word-level memory computing can improve energy efficiency. The middle layer is a column/row level memory-computing layer and has column- or row-shared operation units, such as a linearity compensation module, and a consistency compensation module that improve the performance of multibyte operations. This layer, in which more complex operators can be implemented, balances the energy efficiency, area cost, and power consumption. The uppermost layer is the block-level memory computing layer. Although memory and computing in this layer are loosely coupled, the layer has the highest tolerance for area, power consumption,and delay cost, and it suffers latency and demands a large amount of power in performing operations, data caching,and quantization. The implementation of complex operators in the block-level memory-computing layer can enrich the functions of the CIM system and provide a smooth transition between the CIM system and the traditional von Neumann architecture.

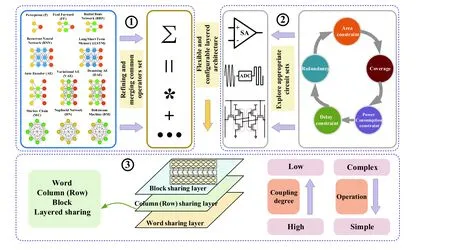
Fig. 25. (Color online) Approach of mapping from the common operator set to the actual circuits.

6.5.2. Optimize the CIM process

The primary steps of CIM include reading and computing, along with a series of processes of writing, quantization,and writeback. The optimization of the entire process, which is key to realizing energy-efficient, high-throughput, and lowarea-overhead CIM, can be performed from the following three aspects, as shown in Fig. 26.

1) A horizontal computing channel can be introduced to implement a bidirectional memory computing system. The intent of SRAM is to introduce computing units into the storage array, reduce data movement, and break through the storage wall. However, in-memory calculations mainly rely on vertical accumulative paths and can only be performed after storage rearrangement, which complicates the calculation process, changing from write → read → calculation → writeback in the von Neumann architecture to write → read → storage rearrangement → write → read–calculation integration→ quantification → writeback. The entire process consumed significantly more energy than the original consumption with von Neumann architecture. Therefore, as shown in Fig. 25, horizontal computational channels can be used to enable CIM without storage rearrangement. Simultaneously, the vertical cumulative path is preserved to make it compatible with the vertical parallel reading techniques; thus, the bidirectional CIM architecture can be implemented with a small area cost.

2) A low-powered fast-migration channel is introduced,and efficient data-storage patterns are designed to reduce the power consumed by migration. It was found that the data used by two adjacent calculations overlapped significantly in the CNN. To improve data utilization and reduce the volume of reloaded data, it is necessary to study the discontinuous data-storage mode to meet the requirements of the algorithm and improve the coupling between computing and storage. Additionally, a fast data-migration channel can perform multiple calculations continuously without reloading data.

3) Memory circuits can be designed based on the reuse/reconstruction/transformation strategy. First, the existing modules of the SRAM memory are fully harnessed. The reusable modules include sensitive amplifiers, BLs, WLs, redundant columns, and decoding circuits. Second, the existing module structure is subtly modified to induce new functions into existing SRAM modules at a markedly low area cost. With the SA as an example, an appropriate configuration transistor can be included to not only induce the amplification and comparison functions into the SA but also generate the SIGMOID function and reconstruct it as part of the ADC (Fig. 25). With the redundant column of a duplicate BL as an example, a small number of switches can be included to transform the redundant column into a pulse-width-generation module that can track the process voltage and temperature variations. The same circuit can be used as part of the operators with different functions through a time-division multiplexing strategy, which greatly reduces the area cost incurred by CIM. Third, the calculation mode is changed from analog domain calculation to digital–analog hybrid calculation, which not only preserves the advantages of analog calculation but also remarkably reduces the difficulty of circuit implementation.

Fig. 26. (Color online) Architecture of the bidirectional CIM system, including a reusable and reconfigurable module.

Fig. 27. (Color online) Multithreaded CIM macro based on a pipeline processor.

6.5.3. Realize the programmability of the SRAM-based CIM architecture

Although traditional computing architectures (such as CPUs and GPUs) are limited in terms of energy efficiency and memory bandwidth, their appeal lies in their general-purpose functions and programmability and their ability to perform various arithmetic operations and execute different algorithms. The existing in-memory technology can achieve several computing functions. However, a few of these CIM macros have poor compatibility with software and limited bitwidth accuracy. Therefore, they cannot execute complex programmable functions and are limited to specific applications.

Interestingly, research on the development of programmable CIMs is underway. For example, Wanget al. proposed a general hybrid memory/near memory computing structure[12], which supports the development of neural networks and software algorithms and offers flexibility and programmability. Jiaet al. proposed a programmable heterogeneous microprocessor[60]and a programmable neural-network reasoning accelerator[59], which can realize a scalable bit width and programmable functions.

The functions that can be realized by existing CIM are relatively simple, and multiple complex operations cannot be performed simultaneously. However, the novelty of CIM is that it solves the problem of storage walls. Therefore, studies have proposed more stringent requirements for the universality and programmability of the CIM architecture. As shown in Fig. 27, to leverage all its advantages, the CIM architecture must be able to implement a multithreaded CIM macro combined with a pipeline processor.

7.Conclusion

CIM technology addresses the limitation of the traditional architecture (i.e., separate storage and computation) and effectively implements AI algorithms. To allow CIM to perform complex operations, the basic cells in the circuit may be modified, and peripheral circuits must be added. This paper detailed the different basic cell structures and peripheral auxiliary circuits of CIM. It also investigated various computing functions that can be realized by the existing CIM framework and their applications. Finally, the challenges encountered by current CIM macros based on SRAM and the future scope of CIM were analyzed. To improve the computational accuracy and capability of the CIM architecture, we recommend efficient mapping the common operators set to a circuit set and optimizing the CIM process under spatiotemporal constraints. Enhancing the programmability of the CIM architecture will enhance its compatibility with general CPUs and enable its wide usage across industries.

Acknowledgements

This work was supported by the National Key Research and Development Program of China (2018YFB2202602), The State Key Program of the National Natural Science Foundation of China (NO.61934005), The National Natural Science Foundation of China (NO.62074001), and Joint Funds of the National Natural Science Foundation of China under Grant U19A2074.