基于数据驱动的园区综合能源系统优化调控方法
2022-03-24陈忠华陈贤卿
陈忠华,徐 强,黄 帅,陈贤卿
(1.杭州市电力设计院有限公司,杭州 310014;2.国网浙江省电力有限公司 杭州供电公司,杭州 310000;3.浙江大学 电气工程学院,杭州 310027)
0 引言
随着风、光等清洁能源的分布式电源技术的快速发展,为了优化能源结构,提高能源效率,许多国家将注意力转向了综合能源系统[1]。由于新能源、信息通信、互联网技术的高速发展,能源系统的供需结构发生了巨大变化,用户不仅是用能主体,还可以作为供能主体或者综合服务商来参与需求响应、电力市场交易等活动。在综合能源系统能量产生和利用的过程中,综合能源系统的优化调度成为基本问题[2]。然而目前的园区存在多种能源使用相互割裂、用能模式不合理、综合能效系统协调互补潜力未能得到充分挖掘等问题,综合能效水平偏低,用能成本偏高,综合能源业务亟需进一步拓展及提升。因此,为充分利用自备可再生能源,减小与大电网功率波动,降低购电成本,在园区包含源、储、荷的综合用能系统中发展先进的能量调度模型具有重要科学意义与工程价值。
在未来园区智慧综合用能系统中,有效的优化调度方法在本地可再生能源接入、降低用能成本、与大电网友好交互等方面起着关键作用。文献[3]针对建筑楼宇优化调度问题,构建了建筑级综合能源系统,并采用基于云模型改进的粒子群算法进行求解。文献[4]构建了计及风电、光伏发电系统出力不确定性和负荷随机性的常规电源和储能装置随机优化日前调度模型。文献[5]分析了园区农业能源互联网发展现状、关键问题和发展趋势,提出了园区农业能源互联网的关键技术和运营模式,并结合不同案例进行分析,为园区农业能源互联网的框架落地和实践提供了参考。为了解决园区综合能源系统日前优化调度中非线性、非凸优化时计算量过大的问题,文献[6]提出了一种“导体和声搜索”算法,来解决日前优化调度问题中的时间序列约束问题。文献[7]提出了一种考虑综合需求响应的综合能源系统容量配置和优化运行方法,并利用差分进化算法和CPLEX求解双层规划模型,最后通过算例分析验证了所提模型的有效性。文献[8]利用双层协调控制框架,在日前调度层完成预调度后,通过拉格朗日公式,考虑储能系统的放电机会成本和边际充电成本,在实时控制层实现调度轨迹的校正。
目前,随着园区各类设备及相关信息系统的不断增加和完善,用能环节产生的数据显示出大数据特征[9]。本文针对园区综合能源系统,提出一种基于数据驱动同时兼顾可解释性的能量调度模型。利用分布式发电与负荷的大量历史监测数据,对多种用能模式进行挖掘,再依据多种时间序列特征提取指标,通过聚类算法得到不同代表性模式。进一步引入参数化的模糊逻辑推理系统,结合启发式算法自趋优地设计涵盖不同模式的模糊推理规则,使得能量调度模型具备广泛的适应性,同时在计算复杂度上满足实时推断需求。本文针对园区能源系统运行优化问题,创造性地提出了数据驱动的混合调度模型,所提方法可以自动地挖掘分析用能特性与自适应设计决策逻辑,以完成在多种运行不确定条件下的系统实时优化控制;同时聚类后所得模式分布与推理规则具有可解释性,可以指导改进并验证算法的有效性。
1 园区综合能源系统
在园区综合能源系统中,包含不可控微型电源(即光伏发电、风力发电等可再生能源系统,其功率输出受自然环境影响,为不可控),可控储能系统与小型热力机组(如热备用的柴油发电机)以及本地负荷,如图1所示。在实时运行调度中,能量管理器需要保证综合用能系统的负荷需求,并尽可能消纳本地自备可再生能源[10]。所提智能混合模型通过对储能系统与小型热力机组的调度控制来实现综合用能系统的最优化运行。

图1 园区综合能源系统结构Fig.1 Regional integrated energy system structure
在图1 所示典型园区综合能源系统中,各个组成部分的功率平衡关系如下

式中:Pres为总的可再生能源(可用的风力发电Pwind和光伏发电PPV);PTUs为小型热力机组单元;Pbalance为负荷Pload和Pres之间的功率剩余或不足,它主要通过储能系统充电或放电,即Pess来匹配功率的剩余或不足,同时小型热力机组也可在功率不足时提供一定支持,Pbalance也对应于没有储能系统及热力机组参与调节时的功率曲线;Pgrid为剩余的功率被吸收或注入到电网。
荷电状态(state of charge,SOC)表示储能系统在当前电量占全部电量的百分比,使用中通常限制在20%至80%。储能系统能量Eess变化由式(4)计算
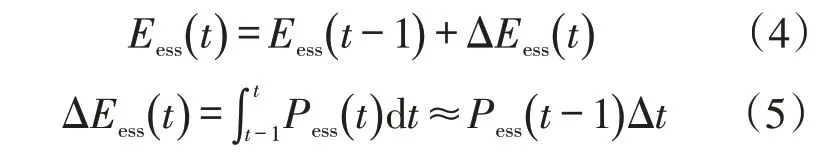
在满足上述功率平衡及控制约束前提下,通过调度策略实现综合用能系统购电及运行成本最小化的经济目标。主要考虑两个方面,一是在考虑实时电价的情况下,微电网从公共电网购买电量的成本,这些花费可以通过向公共电网输出电能抵消,即考虑微电网与主电网之间的潮流是双向的。这里认为公共电网容量远远大于微电网,从而允许微电网的功率反馈至主网。二是考虑小型热力机组的燃料成本。其目标函数如下

式中:Cgrid、CTUs分别为各个时段电网购电与热力机组运行成本;Nint为总的运行时段数;EP为不同时段的电价;a、b、c为热力机组综合花费系数。式(8)中Csum为全时段总的经济目标函数。
系统运行调控过程中要满足如下约束条件

式中:SOCmin、SOCmax分别为储能系统荷电状态最小、最大值;Pess,min、Pess,max分别为储能装置最小、最大充放电功率;PTUs,min、PTUs,max分别为热电机组最小、最大出力值。
2 智能混合调度模型
本文提出一种数据驱动的智能混合模型,引入模糊逻辑处理在不确定性环境下能量调度决策问题。该混合模型包含两个主要模块,其一是根据时间序列提取特征,对大量用能数据进行聚类挖掘,得出园区综合能源系统中的代表性模式。进一步引入模糊逻辑的调度决策方法,利用代表性用能模式自趋优地构建推理规则,得出涵盖广泛模式特性的模糊推理控制器,从而实现对未来新的用能情况进行实时推断决策。其中,模糊推理规则的确定将采用数据驱动方式,在对推理规则集进行编码后,结合第2 节所述用能系统经济目标与用能数据,通过启发式优化算法迭代求解最优的推理规则集。具体模块如下。
2.1 基于时间序列特征的用能模式聚类分析
原始的本地可再生能源发电和负荷数据中包含有海量的运行场景,数据规模极为庞大,而且由于风电、光伏等出力的不确定性和用户负荷数据的周期性,原始的运行场景和用能模式中包含有大量的冗余场景、重复场景和极端场景,这一方面会在很大程度上影响综合能源系统实时调度的精确性,难以实现对综合能源系统的优化调控;另一方面也极大地增加了计算的难度,使得求解效率较为低下。因此,根据时间序列特征对原始的用能数据进行聚类可以有效地去除大量无效的数据,聚类后的各数据场景的属性和特征具有较为明显的差异,这对后续模糊逻辑的引入和实时调控策略的制定具有很大的帮助。
K-means算法是无监督的聚类算法,聚类完成后,作为该类的“类中心场景”,它与该类别内的其他场景具有相似的属性和特征。聚类后每个场景的概率为类别中的场景数除以总的场景数,这既保证了聚类之后场景的概率之和为1,又使得每个场景的概率最大化。
为从大量不同种类时间序列(包括本地可再生能源发电与负荷)中挖掘出有效的用能模式,首先要提取关键特征以反映时间序列曲线的复杂度和波动性等特性,本文从时间序列数据挖掘角度引入以下4个时间序列模式特征。
(1)分箱熵(binned entropy,BE)
把负荷序列X的取值进行分箱操作,可以把[min(X),max(X)]这个区间等分为k个小区间,那么负荷序列的取值将分散在这k个箱中。根据这个等距分箱的情况,就可以计算出这个概率分布的熵
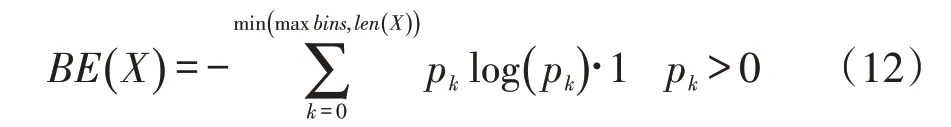
(2)时间序列复杂度不变距离(complexityinvariant distance,CID)
CID值可以衡量负荷曲线数据的复杂度,CID值越大说明该负荷曲线越复杂,波动性越大,具有更多的峰谷

式中:xi为第i个时刻用户负荷数据;n为1天中负荷采样点数;lag为滞后阶数。
(3)时间序列的非线性度量(nonlinear metrics,NM)

式中:xi为第i个时刻用户负荷数据;n为1天中负荷采样点数;lag为滞后阶数。
(4)平均绝对值变化(meanabsolutechange,MAC)

式中:xi为第i个时刻用户负荷数据;n为1天中负荷采样点数。平均绝对值变化是指后一时刻的负荷值和前一时刻的负值绝对值之差的算术平均值,可以反映负荷曲线的波动性。
在构建反映用能模式的特征变量后,所提混合模型以K-means聚类算法[11]为基础对用能系统典型模式曲线进行聚类分析,得出具有相似运行工况的模式类簇。K-means聚类算法是一种基于划分的硬聚类算法。以误差的平方和(sum of squared errors,SSE)作为衡量聚类效果的目标函数。K-means具体算法步骤如下。
步骤1:将m个用户的一天96 点典型负荷曲线M={X1,X2,…,Xm} 提取负荷曲线特征后,M={T1,T2,…,Tm},从原来m×96 维下降为m×10 维,聚类为k个曲线簇S={S1,S2,…,Sk},并任意选择k个初始簇中心μ(ii=1,2,…,k)。
步骤2:计算每条负荷曲线特征Tj(j=1,2,…,m)与簇中心μi的欧式距离d=‖Tj-μi‖,并根据最小距离划分负荷曲线,形成类簇Si(i=1,2,…,k)。
步骤3:以每个类簇中日负荷曲线的均值作为更新后的新聚类中心,即
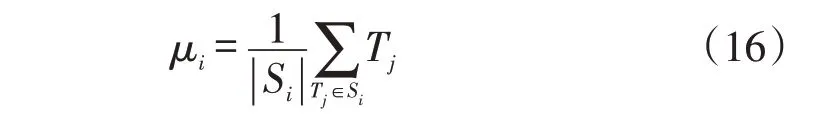
步骤4:重复以上步骤,直到簇中心不再变化。
本文采用“手肘法”[12]来确定K-means的最佳聚类数目k。该方法通过计算SSE,并绘制k-SSE 曲线图,观察图中的拐点来确定聚类数目k。
2.2 自适应模糊推理系统
由于模糊逻辑适合处理不精确信息并具有优良的容错性与鲁棒性,所提模型引入模糊推理系统实现同一类簇用能模式下的最优能量调度。模糊逻辑系统是模拟大脑左半球逻辑思维形式和模糊逻辑推理功能的一种符号计算模型。“它通过‘若—则(IF-THEN)’等规则形式表现人的经验、知识,在符号水平上实现智能地分析输入输出内在的因果关系”。这种符号的最基本形式就是描述模糊概念的模糊集合,因此模型具有一定的可解释性。模糊控制是一种不依赖被控对象的精确数学模型的非线性的智能控制,可以处理不精确或模糊的信息。模糊推理系统具体过程如下:
(1)模糊化是使用隶属函数将清晰输入或实际输入映射到模糊输入的过程。一般用到的输入隶属函数形式为三角锯齿线型或高斯曲线型,输入隶属函数将环境输入(通常先将输入量归一化到适用于隶属函数的某个值),则为隶属函数中的每个模糊集合产生一定程度的隶属度。该值通常由符号μ指定[13]。
(2)模糊推理过程接收上述模糊集合隶属关系,确定相应推理规则来评估输出集的隶属度。当所有输入的隶属度值不为0 时,这些与输入集关联的推理规则将被选择。在对应具体推理规则(以及满足这些标准的其他任何一个)后,推理机根据隶属函数的输入值,可以计算出输出隶属函数的输出度,如式(17)所示
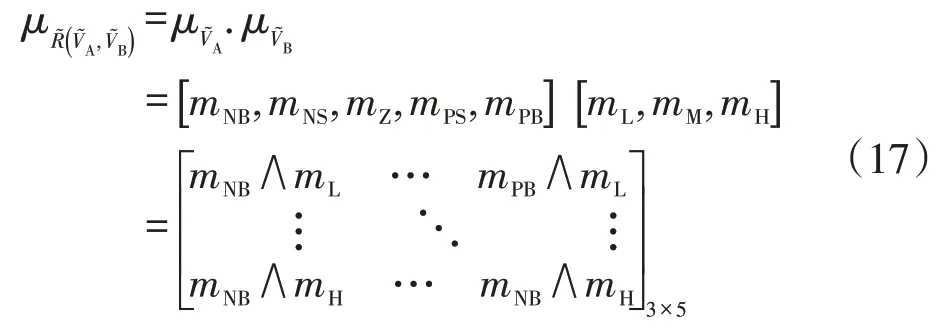
(3)在推理机确定了各输出模糊集的隶属度后,解模糊化过程将这些值转换为输出调度信号。这完全类似模糊化,却是一个相反的过程。通常,会有多个规则被推理机选中(因此输出对应多个隶属度),总的输出值由各个输出集依隶属度加权的质心确定,如式(18)。最后通过尺度变换返回到真实世界输出的水平,如式(19)

在第1 节所代表的典型园区综合能源系统中,模糊推理系统作为调度控制器,其为多输入多输出控制模型。输入部分感知当前运行环境实时状态,输出部分为可控元件(储能系统、热力机组)下一时刻动作的控制信号。感知输入量包括实时电价EP(根据电力市场预测或直接给出)、负荷与可再生能源的差异Pbalance、储能装置当前荷电状态SOC。输出量为储能系统充放电功率Pess(正数代表充电,负数代表放电)和小型热力机组的出力PTUs。在模糊推理系统框架中,首先经过尺度变换将输入量归一化,并由对应的隶属函数分别得出各个模糊集的隶属度。模糊化隶属度函数如图2 所示,负荷与可再生能源的差异Pbalance的隶属函数为锯齿三角形,划分为5 个粗糙集实时电价EP和当前荷电状态SOC的隶属函数均为高斯曲线形。通过模糊推理与解模糊过程可得各个输出量。

图2 输入量模糊隶属度函数Fig.2 Input variable fuzzy membership function
一般情况,模糊推理系统的规则设计要依据不同的控制系统而建立相应的性能指标,其模糊集的选取依据输入输出量的性质,模糊集的数量将决定推理规则的维度。模糊推理系统本质是一种非线性模型,而隶属函数以及目标函数的形式可能进一步增加其非线性程度。因此模糊规则的设计是一个复杂的高维非线性问题。
本文所提模型对推理规则集进行参数化编码,结合具体调控对象将规则设计难题转化为自适应优化求解问题。在模糊化过程中,锯齿三角形隶属函数划分5 个模糊集,高斯曲线形隶属函数划分3个模糊集。
因此,在该模糊推理系统中,模糊推理过程的输入一共有5×3×3=45 种情况,即推断每个输出量需要45个推理规则,因此总的规则集合编码将有90 个优化参数。对于规则中不同模糊语义采用实数编码,即将参数值分段表示不同的语言集合。如式(20)、式(21)所示

因此,在数据驱动方式下求解模糊推理系统时,问题将归结为解维度为104的非凸优化问题,该优化问题的优化目标为所选代表模式下总用电成本最小,每个代表天成本为第2节所述综合用能系统的经济化目标,即式(8),其约束条件满足系统中各功率平衡及运行调控范围约束,即式(9)—式(11)。
在所构建的模糊推理系统自适应参数优化问题中,为有效求解这种复杂的高维非线性优化问题,所提混合模型使用启发式算法进行迭代求解。在启发式算法中最具代表性的为粒子群优化算法(particle swarm optimization,PSO),具有形式简洁、适应性广泛的特点。
在PSO算法中,每个粒子都可以识别并更新其局部最优解(Pbest),并且还可以共同搜索群中的全局最优解(Gbest)[14]。PSO中的位置和速度函数可表示为

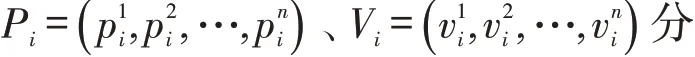
3 算例分析
本文采用图1所示的园区综合用能系统作为算例,园区中自备分布式电源,包括2 000 kW 风力机组、2 000 kW光伏发电、4 500 kW本地负荷、500 kW可控热力机组以及15 000 kWh储能系统,储能装置最大充放电功率为1 500 kW。园区中所涉及时间序列数据来自Open Energy Information[15],对2014年夏季5月至7月数据进行挖掘分析。采用“手肘法”来确定K-means 的最佳聚类数目,令k值从小到大逐渐增大,观察SSE的变化,并绘制k-SSE折线图[16],如图3 所示。观察图3k-SSE折线图可知,选择聚类数k=4 较为合适。

图3 k-SSE 折线图Fig.3 k-SSE line chart
依据聚类所得代表性模式数据对模糊推理系统参数自动求解,从而得出具有可解释性的推理规则集。图4(a)、图4(b)展示了数据驱动方式下所得的调度决策模糊推理规则。依据代表性模式确定了模糊逻辑调度策略后,混合调度模型可以用于未来情况的实时调控。在测试月(8月)选取某一天的工况数据,应用所提混合模型对用能系统进行实时调度,所得储能系统及热力机组出力曲线如图5所示。

图4 模糊推理规则可视化Fig.4 Visualization of fuzzy inference rules
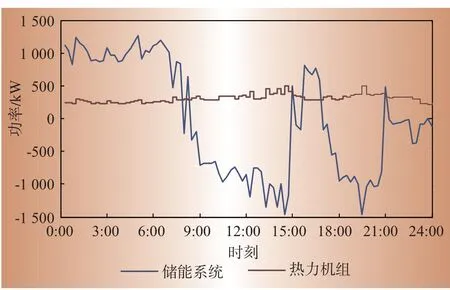
图5 实时调度曲线Fig.5 Real-time dispatching curves
为进一步验证所提混合模型对园区综合能源系统所提升的经济效益,本节将对比基于逻辑规则的控制策略(rule based control,RBC)。RBC 是通过判断输入量的不同情况,根据所属规则自动地决定输出结果。每种输入情况仅对应一种确定的规则。规则是根据所考虑的收益指标要求确定的,即最大程度利用可再生能源;考虑电价波动的购电成本最小;减少储能装置充放电范围。其控制流程如图6所示。
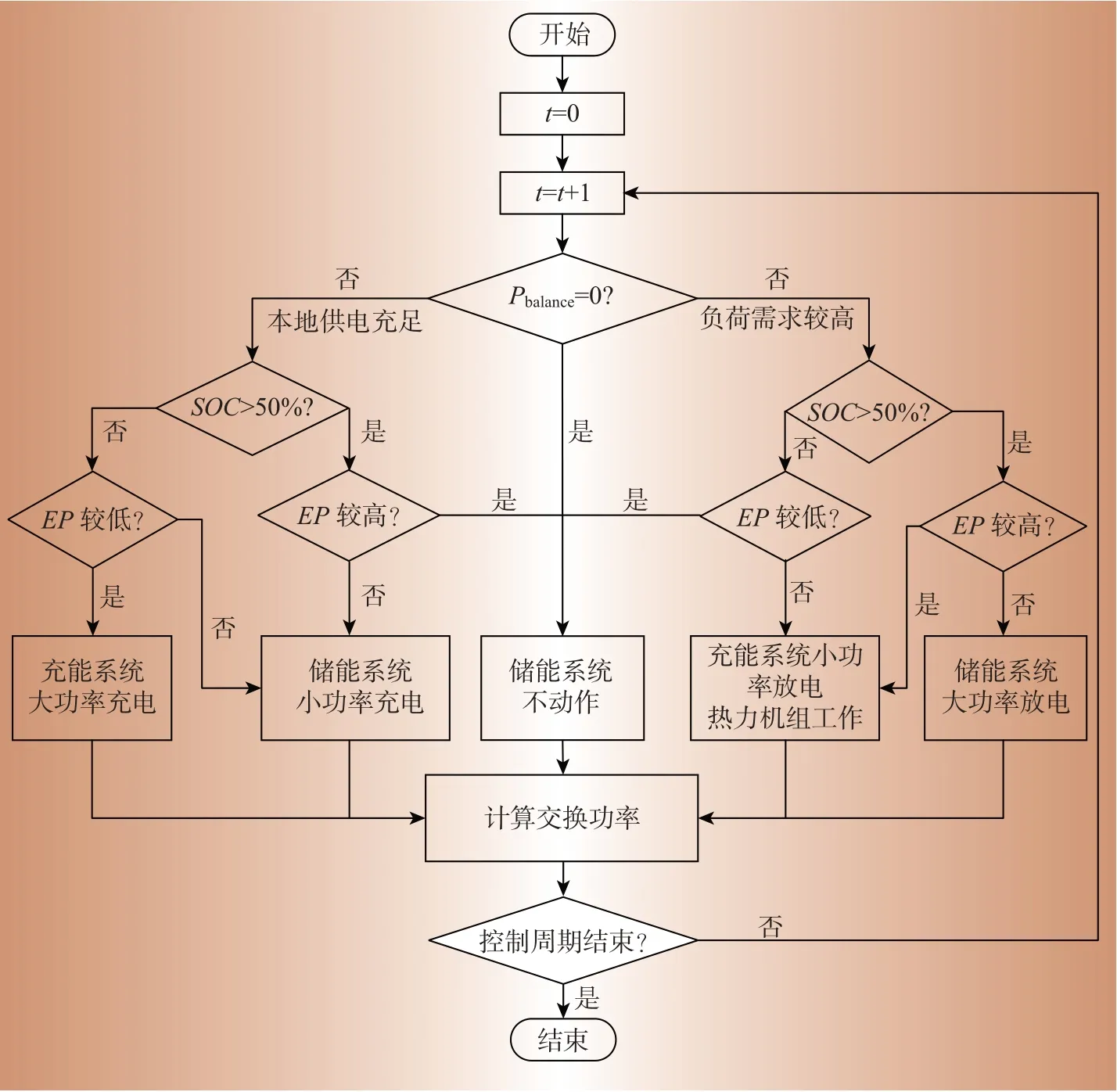
图6 基于规则控制流程图Fig.6 Rule based control flowchart
表1展示了两种调度策略在充分消纳园区本地自备可再生电源后产生的购电成本及运行成本,结果表明所提基于模糊逻辑的调度策略可以明显地降低园区用能系统各项成本。图7展示了两种策略对电网交互功率曲线的“削峰填谷”效果,由图中曲线可知所提策略起到了明显的平缓作用,使得园区综合用能系统对外交换功率更为稳定,可以更友好地接入公共电网。

表1 经济目标对比Table 1 Comparison of economic objectives

图7 对外交换功率比较Fig.7 External exchange power comparison
4 结束语
本文结合用户侧园区综合能源系统多种时间变量的特性指标特征和时间序列特征,基于K-means 聚类算法对不同用能模式进行聚类分析,在得出代表性模式后,通过数据驱动的方式自趋优地设计了基于模糊逻辑的能量调度策略。所提混合能量调度模型可以有效地提升用户侧综合用能系统的经济效益,包括最大化利用本地分布式可再生能源、降低购电及运行成本、对外功率交换平滑等。算例表明在实时控制环境下,本文所提出的模型较对比方法在各项指标上有显著的提升,验证了模型的可行性与有效性。D
