楔形板式相变单元蓄热过程的数值模拟及试验验证
2022-03-24方桂花连小刚
方桂花,吕 程,连小刚,谭 心
(内蒙古科技大学 机械工程学院,内蒙古包头 014010)
0 引言
太阳能等新能源因具有资源丰富、绿色环保等优点受到越来越多的关注[1-2]。但是,太阳能在时空上分布不均匀的特点使其在能量利用方面受到了极大的限制[3],而储能技术[4]的应用就显得非常重要,其中,相变储能技术[5-6]在很大程度上解决了这一方面的问题。
相变储能技术中利用的相变材料(PCM)具有体积小、潜热量大、蓄热过程温度变化小等优点,被广泛应用于太阳能供暖、电子设备散热[7]、余热回收[8]等方面,如谢玲[9]就针对高原地区设计了符合当地的相变蓄热水箱供暖系统,大大提高了太阳能的利用率。但相变材料普遍存在导热系数较低[10]的情况,为了提高其蓄热效率,各种蓄热单元的研究不断展开,其中,板式单元具有面积大,易加工,厚度方向导热性好,易组装的特点,应用较为广泛。KAMKARI等[11]针对局部翅片对矩形相变单元蓄热过程的影响进行了试验研究,证明了通过增加肋片数量可提高单元的蓄热速率,减少PCM熔化的时间。刘孟然[12]用数值模拟的方法研究了附有表面纹理的矩形单元的储热过程,结果表明,有凹槽等纹理的单元可以通过增强对流传热来提高相变材料的蓄热效率。卢一杭等[13]改变了矩形腔体的倾角来观察其内相变材料的融化情况,得出了适当增大单元倾角可以提升相变材料熔化速度的结论。
上述内容中在单元表面添加纹理的方式不易加工,而倾斜单元体会对之后装配的灵活性产生影响,增加翅片是通过增强单元体局部区域的导热性来提升材料的蓄热效率,从整体结构上来提高板状相变单元的研究较少。因而从经济性和易加工性的角度出发,在矩形单元的基础上考虑到相变材料的一些熔化特性,改变整体结构设计了一种楔形板式相变单元。通过数值模拟和试验发现,与同体积的矩形板式相变单元相比,该单元结构在蓄热装置蓄热效率的提升上具有很大的优势,为相变蓄热装置的整体优化设计和工程应用提供了理论基础。
1 蓄热装置模型
1.1 物理模型
研究过程中,将蓄热单元放入蓄热水箱中,蓄热水箱简化模型如图1所示,长为490 mm,宽为447 mm,高为510 mm,进水口在下,出水口在上,两者内径均为25 mm,其中,2种单元均匀分布在水箱里,底部有托板支撑。矩形单元长为300 mm,宽为 40 mm,高为 300 mm,体积为 3 600 000 mm3,表面积为228 000 mm2;楔形单元可以看作一个倾倒的三棱柱,其体积与矩形单元相同,均为3 600 000 mm3,表面积 229 593 mm2,高 300 mm,底面为一个300 mm×80 mm的矩形,除此之外,2种单元所在的水箱模型一致。

图1 矩形单元蓄热水箱和楔形单元蓄热水箱简化模型Fig.1 Simplified models of hot water storage tank for rectangular unit and hot water storage tank for wedge-shaped unit
HTF由下至上经过水箱,在进水口附近放置均流板,以保证相变单元能够与HTF均匀换热。2种单元内都装有有机相变材料石蜡,石蜡的热物性参数见表1。

表1 石蜡的热物性参数Tab.1 Thermal properties of paraffin wax
1.2 模型优化的可行性分析
楔形单元在矩形单元的基础上结合PCM的熔化特性,依照HTF与PCM的换热规律做出如下优化:
(1)PCM由于固液密度有差别,在固相和液相状态同时存在情况下会有固体块沉积底部的现象。在蓄热前期,PCM的接触式熔化占据主导地位,材料液化后的对流换热影响很小,在蓄热单元中PCM由于受重力的作用使得其与受热壁面紧密接触,熔化后的液体材料受到挤压沿壁面排出形成一层极薄的液体层从而获得较高的加热率。而在研究的蓄热装置中,温度较高的换热流体由下至上经过蓄热单元,2种单元的底面是最早受热、温度最高的壁面,也是长时间与PCM接触的壁面。材料熔化的理想示意如图2所示,熔化过程中的固体材料下沉,底部发生接触式熔化,由于楔形单元底面面积两倍于矩形单元,因而具有较大的优势。

图2 两种单元内PCM熔化的理想示意Fig.2 Schematic diagram of ideal PCM melting in the two units
(2)在蓄热过程中HTF与PCM的温差越大,传热效果越好,而流体由下至上经过相变单元时一部分热量被吸收温度逐渐降低,基于这一点,楔形单元合理调整了纵向的体积分布,下部分体积较大,充分利用了这一传热特性,有利于蓄热效率的提高。
(3)经过结构的调整之后,楔形单元在一定程度上增大了与换热流体的接触面积,在两者体积相等的条件下,有利于传热。
1.3 数学模型
对于上述物理模型,PCM的控制方程必须满足如下假设条件:
(1)换热流体为牛顿流体,不可压缩;(2)蓄热装置绝热,忽略热量损失;(3)PCM的热物性参数不会随温度变化而改变;(4)PCM为均质且具有各向同性;(5)忽略相变单元的壁厚;(6)壁面为无滑移边界条件。
基于以上假设,连续性方程为:

式中 ρ ——相变材料密度;
u,v ——PCM沿x,y方向液相速度矢量;
S ——源项;
p ——压强;
Su,Sv——S 在 u,v 上的分量;
Sh——能量方程源项;
H ——相变潜热;
k ——导热系数;
Cp——定压比热容。
2 数值模拟及分析
2.1 数值计算方法
针对相变蓄热问题,借助FLUENT软件,对两种蓄热模型的网格文件进行处理,为了提高仿真的准确性,2种蓄热模型的网格质量一致。在运行程序时,激活能量方程(Energy Equation)和湍流物理模型(k-e),调用Solidification/Melting模型进行蓄热过程的仿真,引入液相率(liquid fraction)的量来表示液化材料占总体容积的比例。通过液相率云图来观测蓄热过程中固液相变材料的分布,利用液相率随时间变化的曲线图来分析整个蓄热过程。
在参数及边界条件的设置上,采用速度进口和压力出口,相变材料以及水箱中流体的初始温度设为30 ℃,不同工况下的入口温度和入口流速参数见表2,通过多组工作条件的仿真模拟,在相同条件下比较2种蓄热单元所在蓄热装置的蓄热性能。

表2 蓄热试验工况设置Tab.2 Setting of thermal storage experiment conditions
2.2 模拟结果及分析
PCM的初始温度为30 ℃,若要满足其相变条件,单元外流体的温度至少要达到57 ℃。在研究的模型中,以蓄热水箱为主体的蓄热装置决定了流体温度的变化是一个循序渐进的过程,整个流体的温度场分布从上至下由低到高出现分层,而两种单元都具有一定的高度,这必然导致即便是在同一种单元表面,不同的高度也会存在温差。图3,4分别示出2种单元中的PCM在工况3条件下3 300 s时的液相率云图,随着高温流体的进入单元下方的水温逐渐升高,单元底部最先达到相变条件,从图中可以看出,由于楔形单元较之矩形单元底面面积更大,会有更多的PCM开始熔化。PCM熔化后密度变小,其上方的固体部分会出现沉降,近乎与底面接触,同样,楔形蓄热单元由于底部空间更大,会有更多的固体材料发生相变,较之矩形单元增大了PCM的熔化速率。

图3 矩形单元内PCM的液相率分布云图Fig.3 Distribution nephogram of liquid phase ratios of PCM in rectangular unit

图4 楔形单元内PCM的液相率分布云图Fig.4 Distribution nephogram of liquid phase ratios of PCM in wedge-shaped unit
在生成的数据文件中,每隔200 s取一点,绘成如下的液相率分布曲线,以此能更清晰直观地表达整个相变过程。图5示出在工况1~3工作条件下的液相率曲线,入口温度均为75 ℃,改变入口流速,液相率大于零时意味着PCM开始相变,液相率达到1时说明相变完成。从图中可以看出在一定范围内,流速越大,蓄热装置完成蓄热过程所用时间越少。同时,每种工况下楔形单元中PCM完成相变过程的时间明显少于矩形单元,这也证实了楔形单元对于整个蓄热装置结构优化的可行性。

图5 不同入口流速下蓄热过程的液相率曲线Fig.5 Liquid phase ratio curves of heat storage process at different inlet flow speeds
此外,从图中还可以看出,前期PCM的相变速率很小,中期开始不断增大,在邻近相变完成时又开始变小,最后逐渐趋于零。这是因为蓄热前期换热流体的温度刚刚超出PCM的相变温度,温差较小,且只有单元底部开始相变。随着蓄热过程的进行,单元内与壁面接触的PCM都开始熔化且换热流体温度大大超过相变温度,整体相变速率提高,直至固体材料所剩极少时速率变小。
图6示出在工况3~5工作条件下,液相率随时间变化的曲线,入口流速均为0.16 m/s,变量为入口温度。从图中可以看到,在一定范围内,流速恒定的情况下,入口温度越高,同一种蓄热装置的蓄热时间越短,同样,每种工况下楔形单元蓄热水箱完成蓄热过程的时间要少于矩形单元。
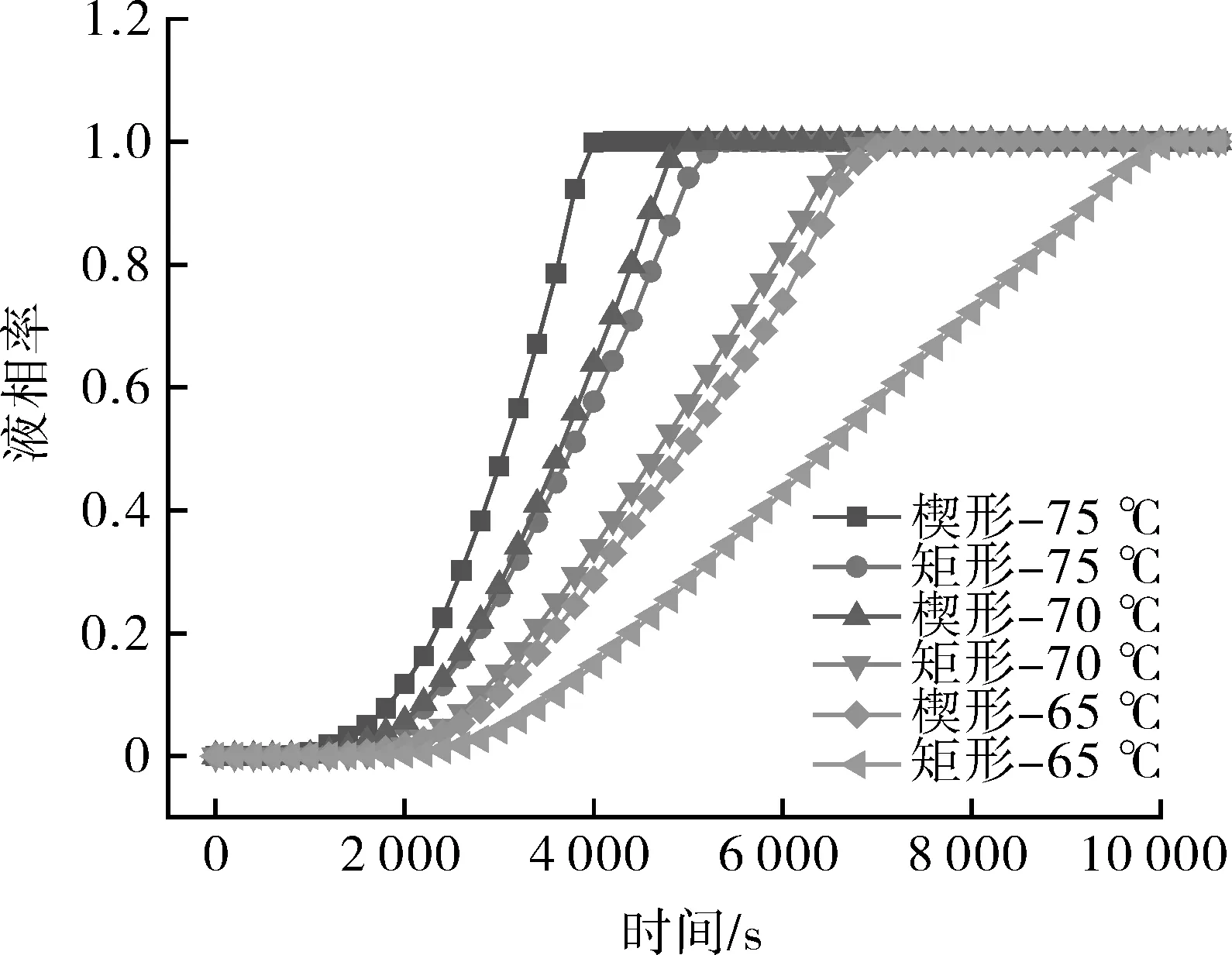
图6 不同入口温度下蓄热过程的液相率曲线Fig.6 Liquid phase ratio curves of heat storage process at different inlet temperatures
3 试验研究
3.1 试验系统
2种蓄热单元外壳所用材料均为304不锈钢如图7所示,在每种单元的上中下3个部位都接有热电阻用来测量其所在部位PCM的温度。2种单元体积相同,将固体PCM熔化之后灌入单元腔体内,然后进行密封。

图7 矩形单元和楔形单元实物Fig.7 The physical pictures of rectangular unit and wedge-shaped unit
完成上述密封操作后,将其进行组装。整个装配体主要由相变蓄热单元、支架、均流板、托板和固定板组成,进行试验时,将所有部件连同支架一同放置在蓄热水箱内。其中,高温流体从水箱下方进水口流入后,先经过均流板,然后依次通过托板、蓄热单元和固定板,最后从上方的出水口流出。
在图8示出的试验流程中可以看到,蓄热试验系统主要由恒温水箱、蓄热水箱(包含蓄热单元)、变频泵、管路、温度巡检仪和显示器构成。
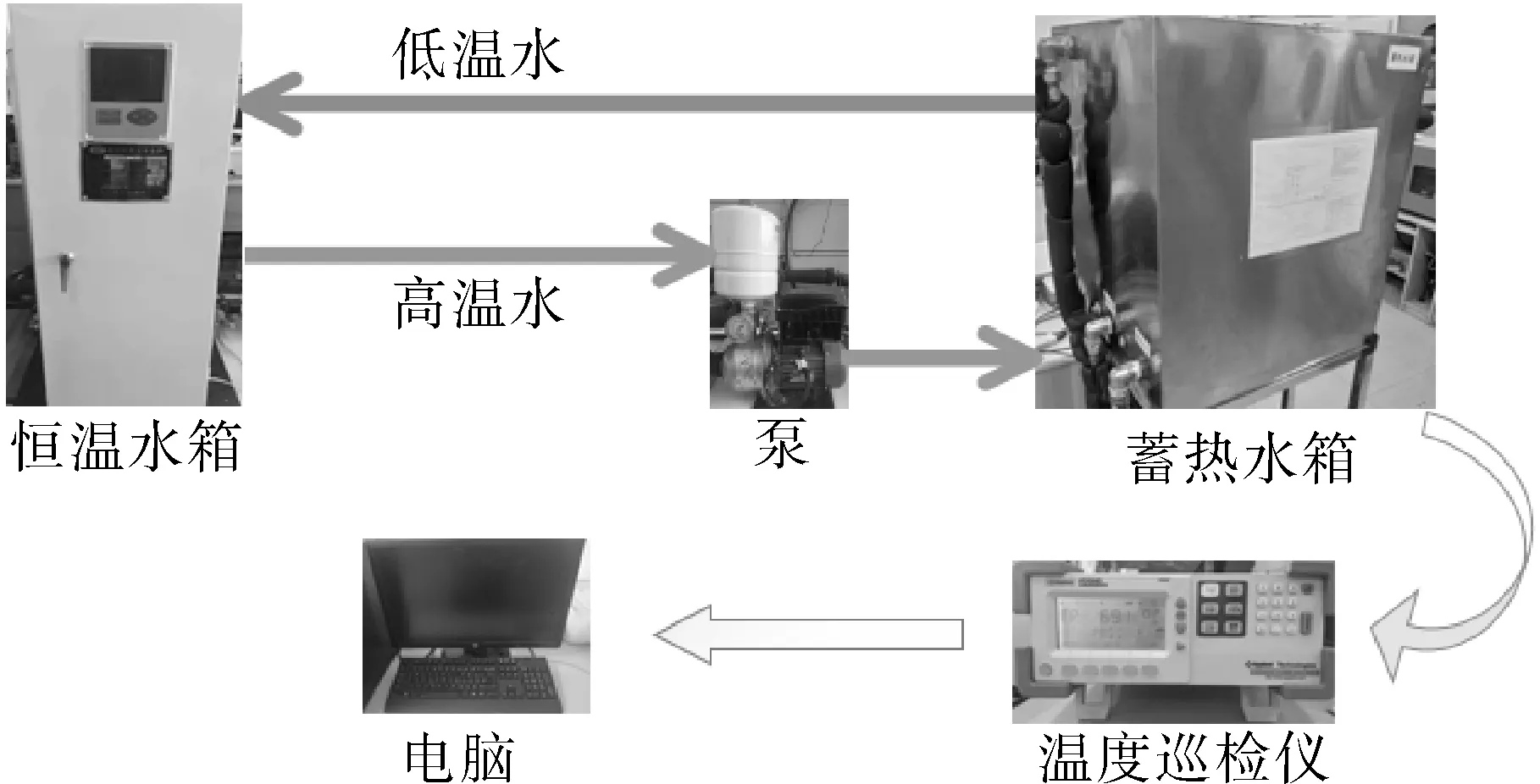
图8 试验流程Fig.8 Experimental flow chart
在试验准备前期,利用恒温水箱将蓄热水箱整体温度调至试验要求的初始温度;试验开始时,将恒温水箱中水的温度稳定至试验所需的入口温度,通过开启变频泵和调节节流阀来控制高温流体流经蓄热水箱,从显示器上监测由温度巡检仪采集的不同测点的温度数据,直至所有测点的温度逐渐趋于平稳时,试验结束。
3.2 PCM的熔化特性分析
图9示出矩形单元蓄热水箱在工况2中不同测点温度随时间变化的曲线。3条曲线的总体变化趋势基本一致,包括显热—潜热—显热蓄热3个阶段。

图9 矩形单元不同测点的温度曲线Fig.9 Temperature curves of different measuring points of rectangular unit
在最开始的显热蓄热阶段,单元下部温度最高,其次是上部,中部温度最低。这是因为高温流体最先经过单元底部,使得下部PCM的温度最先上升,而中部的测点在整个单元的最中心,由于有机相变材料导热性较低使得中部的材料较难受热因而温度低于上部。在潜热蓄热阶段,3个测点温度趋于平缓,单元上部温度最先完成这一过程开始进入显热蓄热阶段,下部温度最后完成潜热蓄热,证明了PCM熔化过程中固体部分发生了沉降,致使液化后的材料被挤压到上部,因而上部升温最快。在下部温度曲线中由潜热阶段过渡到显热阶段对应的时间点可近似视作所有PCM完全熔化的时间,在此工况中,装置内材料完全相变的时间为6 200 s。
3.3 不同工况下的蓄热性能分析
由同一蓄热装置不同测点的温度曲线可以画出其在每种工况下的平均温度曲线,且根据上述方法可以得到2种蓄热装置内PCM平均温度曲线中潜热蓄热完成的时间点,如图10,11所示。在图10中示出的是在入口温度为75 ℃时,入口流速的变化对整个装置蓄热过程性能的影响。从图中可以看到,在这3种工况下楔形单元蓄热水箱完成潜热蓄热的时间明显少于矩形单元,这也印证了模拟结果的准确性,且随着流速的不断增大,同种装置的蓄热时间不断减少。当入口流速分别为0.08,0.12,0.16 m/s时,楔形单元蓄热水箱蓄热时间为 6 650,4 550,4 000 s;矩形单元蓄热水箱蓄热时间为 8 400,6 200,5 200 s。其中,PCM显热阶段温度的增长速率随着流速的增大而增大,这是因为流速的提高增强了自然对流,相应的减小了流体与PCM之间的对流换热热阻,其次,流速的增大使得水箱内升温加快,故显热蓄热升温速率增大。

图10 不同入口流速下蓄热过程的平均温度曲线Fig.10 The average temperature curves of the heat storage process under different inlet flow speeds
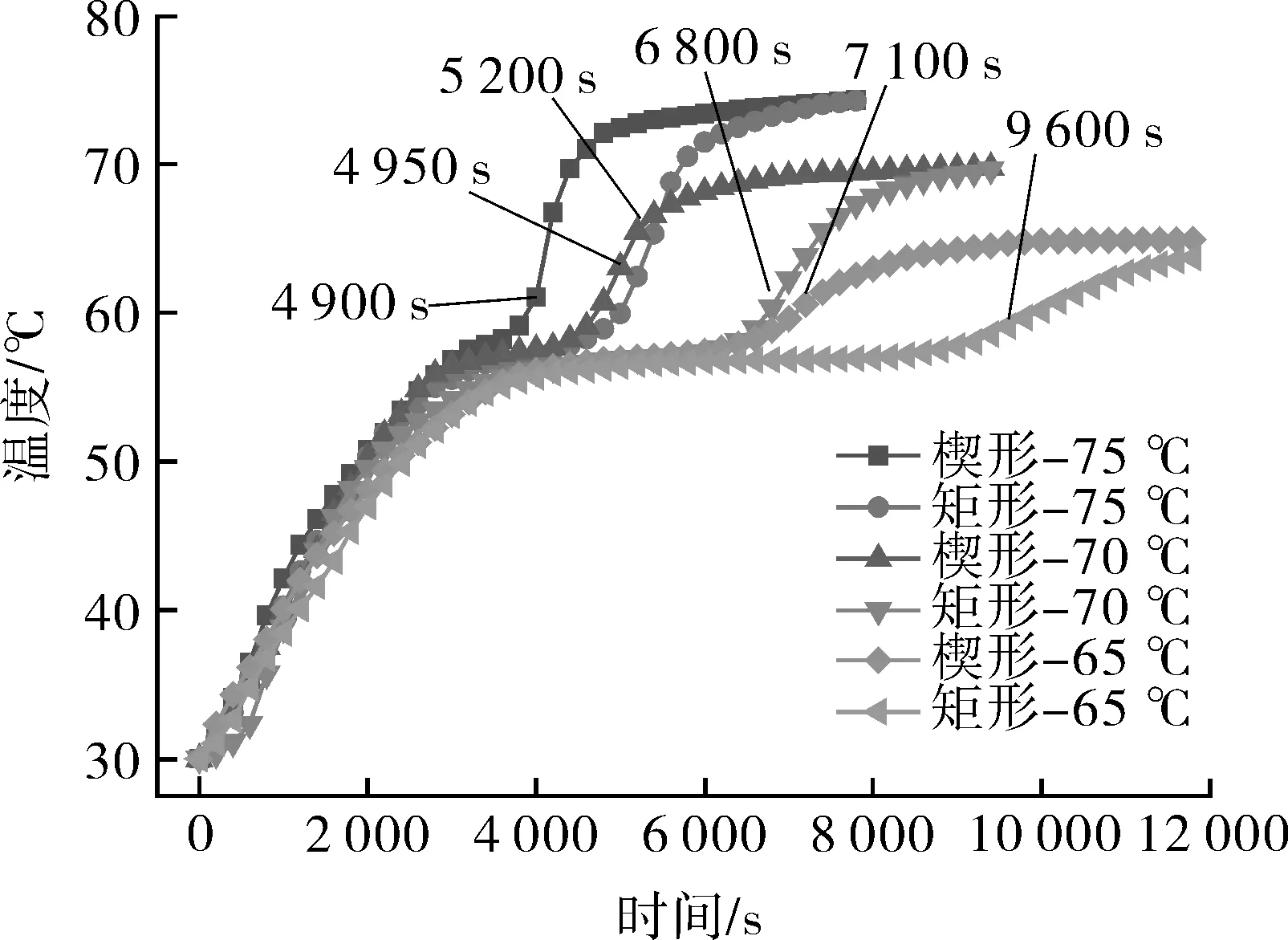
图11 不同入口温度下蓄热过程的平均温度曲线Fig.11 The average temperature curves of the heat storage process at different inlet temperatures
图11示出在入口流速为0.16 m/s时,入口温度的变化对整个装置蓄热性能的影响。从图中可以看到,在这3种工况下楔形单元蓄热水箱的蓄热时间少于矩形单元,当入口温度逐渐增加时,同种蓄热水箱的蓄热时间不断减少。当入口温度分别为65,70,75 ℃时,楔形单元蓄热水箱蓄热时间为 7 100,4 950,4 000 s;矩形单元蓄热水箱蓄热时间为9 600,6 800,5 200 s。其中PCM显热阶段的温度增长速率随着入口温度的增大而增大,由R(导热热阻)=Δt(温差)/Q(热流量)可知,在导热热阻一定的情况下,提高HTF的温度就相应地增大了HTF与PCM之间的温差,使得热流量增大,增强了PCM的吸热速率,故显热蓄热升温速率增大。此外,在不同工况下楔形单元蓄热水箱比之矩形单元蓄热水箱有不同的效率提升,见表3。
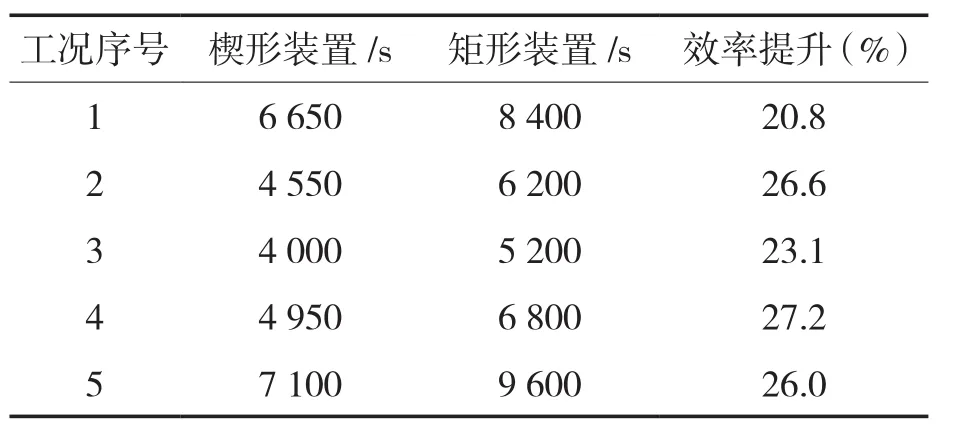
表3 不同工况下的蓄热时间表Tab.3 Heat storage schedule under different working conditions
从表中工况1~3可以看出,在入口温度均为75 ℃时,随着流速的增大,楔形装置对比矩形装置蓄热效率提升分别为20.8%,26.6%,23.1%,流速为0.12 m/s时,楔形装置优势最大;在工况3~5中,流速均为0.16 m/s,入口温度减小时,楔形装置比之矩形装置蓄热效率提升分别为23.1%,27.2%,26%,入口温度为70℃时优势最大。
4 结论
(1)在相同条件下的蓄热过程中,楔形单元内的PCM完全熔化的时间要少于矩形单元,在工程应用中可以根据需要设计合适尺寸的楔形蓄热单元。
(2)入口温度不变,在一定范围内,入口流速越大,两种蓄热装置的蓄热时间越少;入口流速不变,在一定范围内,入口温度越高,两种蓄热装置的蓄热时间越少。
(3)入口温度恒定为75 ℃时,随着入口流速的增大,楔形装置同比矩形装置蓄热效率提升先增大后减小,流速为0.12 m/s时最高,为26.6%;入口流速为0.16 m/s,随着入口温度的提高,楔形装置比之矩形装置效率提升先增大后减小,温度为70 ℃时最高,为27.2%。可见,在实际应用中,要使楔形蓄热装置利用效率最高,需合理地调整进水温度和流速。
