From wave-particle duality to wave-particlemixedness triality: an uncertainty approach

Shuangshuang Fu and Shunlong Luo

1 School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083,China

2 Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China

3 School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

Abstract The wave-particle duality,as a manifestation of Bohr’s complementarity,is usually quantified in terms of path predictability and interference visibility.Various characterizations of the wave-particle duality have been proposed from an operational perspective,most of them are in forms of inequalities,and some of them are expressed in forms of equalities by incorporating entanglement or coherence.In this work,we shed different insights into the nature of the wave-particle duality by casting it into a form of information conservation in a multi-path interferometer,with uncertainty as a unified theme.More specifically,by employing the simple yet fundamental concept of variance,we establish a resolution of unity,which can be interpreted as a complementarity relation among wave feature,particle feature,and mixedness of a quantum state.This refines or reinterprets some conventional approaches to wave-particle duality,and highlights informational aspects of the issue.The key idea of our approach lies in that a quantum state,as a Hermitian operator,can also be naturally regarded as an observable,with measurement uncertainty(in a state)and state uncertainty(in a measurement)being exploited to quantify particle feature and wave feature of a quantum state,respectively.These two kinds of uncertainties,although both are defined via variance,have fundamentally different properties and capture different features of a state.Together with the mixedness,which is a kind of uncertainty intrinsic to a quantum state,they add up to unity,and thus lead to a characterization of the waveparticle-mixedness complementarity.This triality relation is further illustrated by examples and compared with some popular wave-particle duality or triality relations.

Keywords: wave-particle duality, complementarity, mixedness, uncertainty, triality

1.Introduction

The wave-particle duality,ubiquitous in the microworld,is an old and recurring theme in quantum mechanics and is intrinsically related to Bohr’s complementarity principle and Heisenberg’s uncertainty principle [1, 2].The double-slit experiment, which is an archetypal demonstration of the wave-particle duality, is regarded by Feynman as a phenomenon‘which has in it the heart of quantum mechanics;in reality it contains the only mystery’ [3].

Traditionally, one often interprets the wave-particle duality as the statement of observing either the wave feature or the particle feature,but not both simultaneously.However,with the deep investigations of quantum foundations and the emergence of quantum information theory, quantitative studies of the wave-particle duality have attracted much attention for several decades,and considerable new insights have been gained concerning coexistence of partial particle feature and partial wave feature.Historically, Wootters and Zurek were the first to give a quantitative formulation of the wave-particle duality for Einstein’s version of double-slit experiment via an information-theoretic approach [4].Later, Greenberger and Yasin proposed a neat complementarity relation P2+W2=1 for any pure state in a neutron interferometer with P quantifying the particle feature (path predictability) and W quantifying the wave feature (interference) of the state in an interferometric setup[5].By including a path-detector into the interferometer, Englert derived an inequality D2+V2≤1 withD being the distinguishability of the possible detector states andV being a measure of the quality of the interference fringe[6].The equality holds if the particle state and the pathdetector state are pure.Investigations on quantitative measures of wave and particle properties in a multi-path interferometer were initiated by Dürr in [7], where criteria for generalized predictability and generalized visibility were brought up and later further pursued in [8–10].

Quantitative studies of the wave-particle duality have revealed close relationships and interplays between predictability, distinguishability, visibility [4–9], and some quantum informational concepts such as asymmetry [11], entropy[12–14],entanglement[15–20],coherence[21–33],and purity[34].In contrast to the wave-particle duality relations, some triality relations involving wave (as quantified by fringe visibility), particle (as quantified by predictability or distinguishability),entanglement(or coherence),were obtained in[15–20].For examples,Jakob and Bergou established[16],in a bipartite system, the following triality relation= 1,k=1, 2,where k refers to the two parties of the system,Vkis fringe visibility, Pkis predictability, and C is concurrence (a measurement of entanglement) [35, 36].Qureshi established another triality relation C + PQ+ EQ=1between predictabilityPQ, quantum coherenceC and entanglementEQin an n-path interferometer with a path-detector [20].Basso and Maziero obtained a triality(complete complementarity relation)for quantum uncertainty, classical uncertainty, and predictability in [33].Qian and Agarwal established a Pythagorean type relation between the wave feature, particle feature, and purity of a source state[34].

Quantum states and observables are two simple yet fundamental concepts in quantum mechanics [37, 38].Their coupling generates fruitful results in quantum information theory.Uncertainty, which is inevitable in quantum mechanics and actually underpins almost all fields in quantum information theory, relies on these two concepts.Recall that the conventional variance of measuring a quantum observable X in a quantum state ρ is

As a fundamental measure of uncertainty, variance plays an important role in both quantum foundations and quantum experiments.Usually,ρ is only regarded as a state.However,since a state is a priori a Hermitian operator, it can also be regarded as an observable, and consequently its variance under some other reference states may be exploited to reveal certain features of the state.This leads to the following variance of a state in a measurement

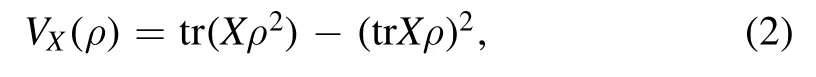
which is a dual version of the conventional variance defined by equation(1).Here X is regarded as a reference state(rather than an observable).Despite the innocuous appearance of the defining equation (2), the above two versions of variance are fundamentally different:Vρ(X)is concave in ρ,while VX(ρ)is convex in ρ.To distinguish them more explicitly, we introduce the following terminology when the observable X can also be regarded as a state:

There are significant consequences for the state uncertainty VX(ρ).For example, a quantifier of optical nonclassicality arises naturally when considering state uncertainty of ρ(regarded as an observable) in the family of Glauber coherent states [39], and coherence based on the Hilbert–Schmidt distance of ρ may be identified as state uncertainty of ρ (regarded as an observable) in the incoherent basis [40].

In this paper, we establish a complementarity relation in terms of uncertainty, and relate it to the wave-particle duality.Employing the two complementary versions of uncertainty based on variance, i.e.measurement uncertainty and state uncertainty, we construct reasonable measures of both predictability and visibility,which summarize the particle feature and wave feature, respectively.Furthermore, we give a neat yet intrinsic triality relation between the wave feature, particle feature, and mixedness of a state, all involving only uncertainty.We emphasize that although our triality is mathematically equivalent to those in [7, 15, 16, 34], the physical meanings are quite different,as will be elaborated in the remaining sections.A key feature of our triality is that all quantities are naturally expressed as uncertainty derived from variance,and thus is conceptually less complicated than other ones.

The remainder of the paper is arranged as follows.In section 2, we briefly review some existing quantifications of the wave feature, particle feature and the duality relations for both two-path and multi-path interferometers without detectors.In section 3, we discuss some basic and plausible requirements that should be satisfied for reasonable quantifiers of wave feature and particle feature.We introduce quantifiers of predictability and visibility based on measurement uncertainty and state uncertainty, respectively, and establish an intrinsic wave-particle-mixedness triality relation in section 4.In order to illustrate the effectiveness of the measures proposed, we analyze an n-path interferometer without a detector and make a comparative study in section 5.We conclude with a summary in section 6.For simplicity,we only work in finite dimensional systems.

2.Wave-particle duality

In this section, we briefly review some well-known waveparticle duality relations, which motivate our study.For simplicity, here we do not consider the situations involving detectors.We emphasize that whenever we talk about the wave-particle duality, we are always referring to the wave feature and particle feature of a quantum state with respect to a specific setup such as a computational basis (or the corresponding measurement) arising from the path configuration of an interferometer or similar apparatus.

Figure 1.State preparation of a two-path interferometer in Greenberger–Yasin’s investigation of the wave-particle duality: the wave feature and particle feature with respect to the computational basis{|0〉, |1〉} refer to those of the intermediate pure state |ψ〉 generated by passing the input state through the first beam splitter [5].

2.1.Greenberger and Yasin [5]

After Wootters and Zurek firstly gave a quantitative version of the wave-particle duality in the two-slit diffraction experiment[4],Greenberger and Yasin investigated the waveparticle duality in a neutron interferometer and obtained a nice characterization of the wave-particle duality[5].The relevant setup is depicted in figure 1,where the pure state after the first beam splitter is described as

and the wave-particle duality refers to the properties of |ψ〉with respect to the computational basis {|0〉, |1〉} (or equivalently, the corresponding von Neumann measurement Π={|0〉〈0|, |1〉〈1|}) determined by the two paths.Herea,b∈ C , ∣a∣2+ ∣b∣2=1.Greenberger and Yasin proposed the following quantifiers (up to suitable normalization)

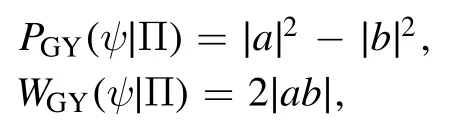
as a particle measure and a wave measure (contrast of the interference pattern) of the state, respectively.They further derived the following complementarity relation

for any pure state |ψ〉, which is mathematically equivalent to the normalization condition |a|2+|b|2=1 for the state|ψ〉=a|0〉+b|1〉.Since we will encounter several other different measures of particle feature and wave feature,we have to use the subscript to distinguish them.Consequently, we adopt notations different from Greenberger and Yasin [5].

2.2.Englert [6]

Englert studied the fringe visibility and predictability in a two-path interferometer, and established a wave-particle duality relation with/without a path detector.We only recall here the relevant result without a path detector, which is depicted in figure 2.

For the state(in general mixed,in contrast to that in figure 1)

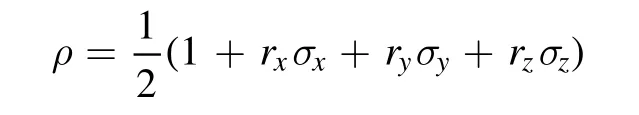
prepared by the frist beam splitter, whererx,ry,rz∈R,and σx, σy, σzare the Pauli matrices,Englert derived the following inequality [6]

Figure 2.State preparation of a two-path interferometer in Englert’s investigation of the wave-particle duality: the wave feature and particle feature with respect to the computational basis {|0〉, |1〉}refer to those of the intermediate mixed state ρ generated by passing the input state through the first beam splitter[6].Though the setup is completely similar to that in figure 1, we depict it in this figure to emphasize that mixedness of the state yields significant difference for the wave-particle duality.

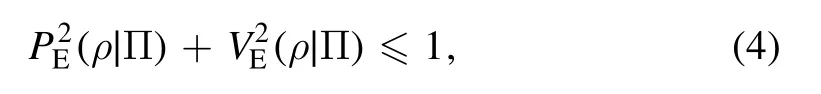
where Π={|0〉〈0|, |1〉〈1|} is the von Neumann measurement induced by the computational basis{|0〉, |1〉} (two paths), while

and

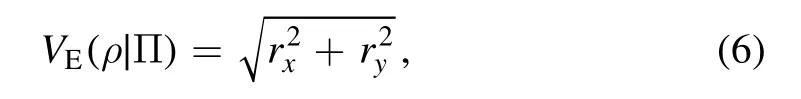
are the path predictability and prior fringe visibility,respectively,of ρ.Inequality (4) illustrates, in a two-path interferometer, a duality between the wave feature (fringe visibility) and particle feature(which-path information that is potentially stored).For any pure state, the result reduces to equation (3) of Greenberger and Yasin [5].

2.3.Qian and Agarwal [34]

Qian and Agarwal investigated the duality of a photon generated from genuine point sources and established a Pythagorean type duality relation in[34].They showed that the amount of information available for exchange between the photon’s wave feature and particle feature is related to the state purity.More explicitly, for a qubit state ρ=(1+rxσx+ryσy+rzσz)/2, they employed

and

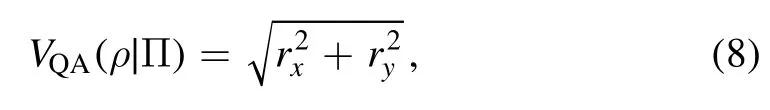
as quantifiers of particle feature and wave feature(the same as Englert’s equations (5) and (6)), respectively, and went further to establish the following duality relation

2.4.Dürr [7]

Dürr initiated the study of quantitative measures of wave and particle properties in a multi-path interferometer in [7].The preparation setup for a general n-path interferometer is sketched in figure 3.The n different paths are represented by the computational basis {|i〉:i=1, 2, …, n}, with the corresponding von Neumann measurement Π={|i〉〈i|:i=1, 2, …, n}.The quantum state ρ, which is obtained by passing the input state through the first beam splitter, can be expressed in the computational basis as

Figure 3.State preparation of an n-path interferometry in Dürr’s investigation of the wave-particle duality: the wave feature and particle feature with respect to the computational basis {|i〉:i=1, 2, …, n} refer to that of the intermediate mixed stateenerated by passing the input state through the first beam splitter [7].

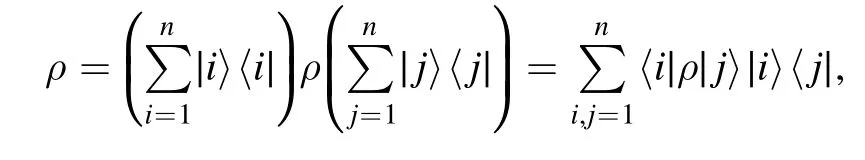
and one is interested in its particle feature and wave feature with respect to the computational basis (equivalently, the von Neumann measurement Π).The wave-particle duality established by Dürr can be expressed as [7]

with the predictability and visibility given by

respectively.Furthermore, based on equations (10) and(11), Dürr established the following complementarity relation

which can be regarded as a triality relation.After simple manipulation, this triality can be transformed into a form which is mathematically (but not physically)equivalent to our triality relation, as will be discussed in section 5.

2.5.Jacob and Bergou [15, 16]

Jacob and Bergou investigated the complementarity in a bipartite quantum system of arbitrary dimensions and established that generalized predictability and visibility can be attributed to single-partite properties, while these properties are exclusive to the genuine bipartite correlations of the system [15, 16].Employing the expectations of a group of generators, they established the following complementarity relation [15]

with their measures of predictability and visibility defined as

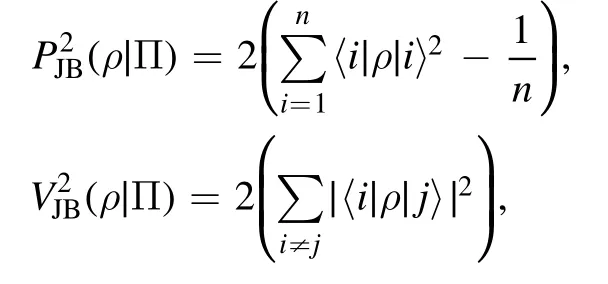
respectively.This triality relation is also mathematically equivalent to equation (12), but the physical meanings are different.

3.Wave versus particle: quantitative aspects

We review in this section some quantitative aspects of the wave-particle duality in a general n-path interferometer[7–10], as sketched in figure 3.The n different paths are denoted by the computational basis{|i〉:i=1,2, …, n}.The induced path observable is denoted by Π={|i〉〈i|:i=1, 2,…, n}.Any quantum state ρ, which is obtained by passing the input state through the first beam splitter,can be expressed in the computational basis as

A quantification of the wave feature (interference)involves two objects,a state ρ and a set of paths{|i〉:i=1,2,…, n} (or equivalently Π={|i〉〈i|:i=1, 2, …, n}).In this paper,we denote it asW(ρ∣ Π ).Following[7–9],we postulate that it satisfies the following plausible requirements:

(a)W(ρ∣Π ) reaches its global minimum if the state ρ is classical (i.e.diagonal in the computational basis).

(b)W(ρ∣Π ) reaches its global maximum if ρ is pure and a uniform superposition of the states in the computational basis, i.e.〈i|ρ|i〉=1/n for all i.

(c)W(ρ∣Π )is invariant under permutations of the diagonal elements 〈i|ρ|i〉 of ρ.

(d)W(ρ∣Π ) is convex in ρ.

In a dual fashion, a quantification of the particle feature(predictability)measures the path information of a state ρ with respect to a path measurement Π,and is denoted asP(ρ∣Π ).It should have the following properties [7, 9]:

(a)P(ρ∣Π ) reaches its global maximum if 〈i|ρ|i〉=1 for some i.

(b)P(ρ∣Π ) reaches its global minimum if 〈i|ρ|i〉=1/n for all i.

(c)P(ρ∣Π ) is invariant under permutations of the diagonal elements 〈i|ρ|i〉 of ρ.

(d)P(ρ∣Π ) is convex in ρ.

All the above mathematical requirements are motivated by intuitive physical considerations [7–9], and are satisfied by the quantities reviewed in section 2.We remark thatW(ρ∣Π )will be quantified via state uncertainty,P(ρ∣Π ) will be quantified by path certainty (with the inverted quantity corresponding to the path uncertainty).

4.Wave-particle-mixedness triality

In this section,we introduce three figures of merit quantifying the wave feature, particle feature and mixedness, all in terms of uncertainty.We establish a quantitative wave-particlemixedness triality as a resolution of unity.This refines or reinterprets some conventional wave-particle relations on one hand,and provides a simple information conservation relation capturing Bohr’s complementarity on the other hand.Different from the conventional operational approach, all quantities in our approach are simply defined via variance in a unified fashion, thus shed different insights into the informational aspects of wave-particle complementarity.

4.1.Quantifying wave feature via state uncertainty

Following[39],by regarding the state ρ as an observable and considering uncertainty of ρ(in the paths)as quantified by the sum of variance of ρ in all path states |i〉, we introduce the state uncertainty

as a measure of the wave feature of ρ(in Π).It turns out that

Moreover, from equation (14), we obtain an equivalent expression ofW(ρ∣Π ) as

We argue thatW(ρ∣Π ) as defined above can be regarded as a measure of interference potential for the quantum state ρ in the basis {|i〉:i=1, 2, …, n}.Indeed,W(ρ∣Π ) has the following desirable properties,as required by such a quantity:

for a set of probabilities piand quantum states ρi.

All the above properties can be directly verified, and are consistent with the requirements postulated in section 3.

4.2.Quantifying particle feature via measurement(un)certainty

Given a quantum state ρ, the traditional measurement uncertainty of performing the path measurement Π={|i〉〈i|:i=1,2, …, n}is quantified by

which is the sum of variance of the measurement operators(effects)|i〉〈i|in the state ρ.It turns out that

This quantity captures uncertainty when one tries to detect the particle path,with the minimal uncertainty corresponding to the maximal path information,and thus is an inverted measure of path information.Consequently, the complementary quantity 1-U(ρ∣Π ) can be regarded as a measure of the degree of particle certainty, which reveals the path distinguishability information.We denote it asP(ρ∣ Π ),i.e.

It can be easily verified thatP(ρ∣Π ) meets the criteria for a reasonable quantification of the particle feature(predictability),as described in section 3.Indeed,P(ρ∣Π ) has the following properties.

(a)P(ρ∣Π ) depends explicitly only on the diagonal elements of the density matrix of ρ in the computational basis {|i〉:i=1, 2, …, n}, and is invariant under permutations of the diagonal elements.

(b)1/n≤ P(ρ∣Π )≤ 1.The minimal value is obtained if〈i|ρ|i〉=1/n for all i, while the maximal value is obtained if 〈i|ρ|i〉=1 for some i.

(c)P(ρ∣Π ) is convex in ρ.

Consequently,P(ρ∣Π ) is indeed a quantification of the path information of the state ρ when the n paths are represented by the measurement Π={|i〉〈i|:i=1, 2, …, n}.

4.3.Quantifying mixedness via Brukner-Zeilinger invariant uncertainty

For a general quantum state ρ in a d-dimensional system Hilbert space,a simple and basic measure for its mixedness is

which is precisely the widely used linear entropy (Tsallis 2-entropy) of ρ and is complementary to the puritytr2ρ.Brukner and Zeilinger presented a remarkable meaning of the above quantity by regarding it as the sum over all individual measurement uncertainties for a complete set of mutually complementary experiments, which can be cast as a measure of uncertainty derived from variance[41–43].For this reason,M(ρ) is also called the Brukner–Zeilinger invariant uncertainty, and is closely related to the Brukner–Zeilinger invariant information [41, 42].Of course, there are many other measures of mixedness,andM(ρ)stands out by its simplicity and informational significance.

The mixednessM(ρ)has the following basic properties:

In our information-theoretic approach to the wave-particle duality, the key idea is to distinguish the measurement uncertainty of Π (in the state ρ) and the state uncertainty of ρ(in the measurement Π).We list these fundamentally different yet complementary quantities together with the mixedness in table 1 for a clear comparison.

Table 1.Various uncertainties.

4.4.Wave-particle-mixedness triality

Recall that we have introduced three quantities,W(ρ∣Π ),P(ρ∣Π )andM(ρ),all based on uncertainty in a unifeid fashion and defined independently with respect to each other.Now combining equations (14)–(16), we immediately obtain

which is an identity,and thus signifies information conservation.This is our triality relation.We emphasize that the three quantities appearing in the left hand side of equation (17) are all measures of uncertainty with different attributes.More explicitly,

(a)W(ρ∣Π )summarizes the state uncertainty of ρ(in the von Neumann measurement Π induced by the paths),and can be regarded as a quantifier of interference potential.Large state uncertainty means large coherence,or equivalently,large potential for interference(fringe visibility).

(b)P(ρ∣Π ) quantifiers the measurement (un)certainty of Π induced by the paths (in the state ρ), and can be interpreted as a quantifier of path-detecting capability.Small measurement certainty (large uncertainty) means little information about the path.

(c)M(ρ)measures the uncertainty intrinsic to the state itself,as such,it can also be regarded as the capability of establishing correlations(entanglement)with other systems.

The fact that the above three uncertainties add up to unity,which constitutes our triality (in contrast to the conventional duality), is a manifestation of the complementarity between the particle feature, wave feature, and mixedness of the quantum state ρ.This triality (complementarity) is depicted,under the unified theme of uncertainty, in figure 4.

Figure 4.Wave-particle-mixedness triality as a resolution of unity:W(ρ ∣Π )quantifies the uncertainty of state ρ in the paths described by Π and is interpreted as indicating the wave feature of the state,P(ρ ∣Π ) quantifies the measurement certainty of Π in the state ρ and is interpreted as indicating the particle feature of the state,M(ρ )quantifies the intrinsic mixedness of the state ρ.These three kinds of uncertainties add up to unity.This constitutes our wave-particlemixedness complementarity in a form of information conservation.

We consider some extreme cases of the triality relation (17):

We summarize the above intuitive observations in table 2.

Table 2.Some extreme cases for the triality relation W( ρ ∣Π ) + P( ρ ∣Π ) + M(ρ ) =1.

5.Illustration and comparison

In the above section, we have introduced measures of predictability and visibility in a general n-path interferometer in terms of uncertainty quantified by the ubiquitous variance.As has been demonstrated, both these measures (measurement uncertainty and state uncertainty) are nicely captured by variance.A triality relation for the wave feature, particle feature and mixedness is established as a resolution of unity.

In this section, we illustrate the triality relation in an n-path interferometer and compare our results with those of Englert [6], Qian and Agarwal [34], Dürr [7],Jacob and Bergou [16].Consider the state ρ=(1+rxσx+ryσy+rzσz)/2 after the first beam splitter, as illustrated in figure 2.The path information can be quantified byP(ρ∣Π ) and the wave information can be quantified by W(ρ∣ Π ) with Π={|0〉〈0|, |1〉〈1|}.From equations (14) and(15), it can be readily evaluated that

We also calculate the corresponding quantities reviewed in section 2.In this context, Englert’s equations (5) and (6),Qiang-Agarwal’s equations (7) and (8), as well as Dürr’s equations (10) and (11), coincide.

In table 3, we make a comparison of our result with Englert’s result in [6] and Qian–Agarwal’s result in [34].Furthermore, we compare our result with Dürr’s and Jacob–Bergou’s results in table 4.We notice that the relation given by Dürr in equation(12)can be more succinctly expressed as

Table 3.Comparisons between our result, Englert’s duality,Qian–Agarwal’s duality, for a qubit state.Here ρ=(1+rxσx+ryσy+rzσz)/2,Π={|0〉〈0|, |1〉〈1|}.

Table 4.Comparisons between our result, Dürr’s result and Jacob–Bergou’s result.Here Π={|i〉〈i|:i=1, 2, …, n}, ρij=〈i|ρ|j〉.

which is clearly a kind of triality relation.It can be readily seen that our quantities are simply connected with Dürr’s and Jacob–Bergou’s from the mathematical viewpoint.The expressions of the wave, particle and mixedness differ only by dimensiondependent scaling factors and constant shifts.Physically,equations with different coefficients and shifts can not be regarded as the same one.Thus the three triality relations are different.Indeed,the quantities involved in these three triality relations have quite different physical meanings.All the three quantities in our approach are defined via uncertainty in a unified fashion.It is remarkable that these physically different approaches lead to mathematically similar relations.These are more transparently illustrated in table 4.

6.Summary

In this work,for a given quantum state ρ and a computational basis induced by the path configuration,we have analyzed the uncertainty of the state ρ in the path configuration from different perspectives by putting either the state or the measurement in an active place, with the other in an inactive place (as a background).The key idea lies in that ρ, although is often only regarded as a quantum state, can also be regarded as an observable.Thus here the state plays a dual role as both a state and an observable.This leads us to distinguish two versions of variance: measurement uncertainty and state uncertainty.We have demonstrated that suitable measures of predictability(particle feature)and visibility(wave feature)can be built from them.Furthermore,a triality relation is established between the wave,particle and mixedness of the quantum state.

We have illustrated the triality relation in an n-path interferometer,and have compared it with previous characterizations.Our quantification, on one hand, is consistent with previous results, on the other hand, can be easily calculated and has an informational interpretation as uncertainty.

Most quantitative studies of wave-particle duality adopt an operational approach based on various path-distinguishability measures and fringe visibility quantities.We emphasize that our approach, employing the single concept of uncertainty, is information-theoretic and is quite different from previous methods, though the mathematical results are closely related.The reduction of wave-particle duality to uncertainty decomposition, as symbolized by the triality relation, equation (17), provides alternative insights into the nature of the wave-particle duality and may be helpful in revealing information-theoretic aspects of the wave-particle duality.

Our triality involves state uncertainty and measurement uncertainty, while the conventional Heisenberg uncertainty relation involves measurement uncertainties of incompatible observables.Although it is widely recognized that waveparticle duality and the Heisenberg uncertainty relation are intrinsically related,quantitative and precise characterizations of relations between them are relatively less studied.It is an interesting issue to further clarify the links between the duality (triality) relation and the Heisenberg uncertainty relation,which will be a future project.

The quantities we proposed from the theoretic point of view can be associated with measurable quantities since all are defined via variance.We have considered only the situation when there is no detectors involved.The measures we proposed are characterizations of the wave feature and particle feature of a quantum state itself in a multi-path configuration.In many practical situations, the detectors are attached to obtain path information of the quantum state.It would be interesting to investigate the corresponding waveparticle-mixedness relations and associated information exchange in this more general setup.

Acknowledgments

This work was supported by the National Key R&D Program of China, Grant No.2020YFA0712700, the Fundamental Research Funds for the Central Universities, Grant No.FRFTP-19-012A3, and the National Natural Science Foundation of China, Grant Nos.11 875 317 and 61 833 010.