Representation of the coherent state for a beam splitter operator and its applications
2022-03-23MingxiaZhanFangJiaJialiHuangHuanZhangandLiyunHu
Mingxia Zhan, Fang Jia,*, Jiali Huang, Huan Zhang and Liyun Hu,2,*
1 Center for Quantum Science and Technology, Jiangxi Normal University, Nanchang 330022, China
2 Institute for Military-civilian integration of Jiangxi province, Nanchang 330029, China
Abstract A beam splitter operator is a very important linear device in the field of quantum optics and quantum information.It can not only be used to prepare complete representations of quantum mechanics, entangled state representation, but it can also be used to simulate the dissipative environment of quantum systems.In this paper,by combining the transform relation of the beam splitter operator and the technique of integration within the product of the operator, we present the coherent state representation of the operator and the corresponding normal ordering form.Based on this, we consider the applications of the coherent state representation of the beam splitter operator, such as deriving some operator identities and entangled state representation preparation with continuous-discrete variables.Furthermore,we extend our investigation to two single and two-mode cascaded beam splitter operators, giving the corresponding coherent state representation and its normal ordering form.In addition, the application of a beam splitter to prepare entangled states in quantum teleportation is further investigated, and the fidelity is discussed.The above results provide good theoretical value in the fields of quantum optics and quantum information.
Keywords: beam splitter operator, coherent state representation, the technique of integration within product of operator, quantum teleportation
1.Introduction
A beam splitter(BS)has many applications in quantum optics and quantum information.For example,a beam splitter can be used to prepare non-classical quantum states, prepare complete representations of quantum mechanics,and simulate the loss process of quantum states, including photon loss(amplitude attenuation), thermal environment, etc.Specially speaking, when an ideal coordinate state and a momentum state are input into a BS, an ideal entangled state representation can be obtained [1].By using two asymmetric BSs and conditional measurement of single photon, Liu et al prepared a class of non-classical quantum states, and discussed its related properties [2].Based on the Knill–Laflamme–Milburn interferometer composed of three asymmetric BSs,Xu et al realized a kind of non-Gaussian state and discussed non-classical properties [3].In addition, if the vacuum is input to one port of the BS, and the output port is free (i.e., trace the mode), then the process can simulate the amplitude attenuation, where the transmittance of the BS is related to the attenuation.
On the other hand,quantum entanglement is an important resource for realizing quantum information tasks.Facing the real situation where the entanglement degree of the prepared entanglement source is low,lots of researchers have proposed methods that use non-Gaussian operations [4–22], such as photon addition, photon subtraction, photon catalysis, etc, to further increase the degree of entanglement.Using these proposed states as entangled sources, quantum tasks can be better implemented,such as quantum teleportation.In fact,in order to achieve the above operations, the BS plays an important role.For instance, when one port of the optical BS inputs the vacuum state and the other end performs the photon number detection operation, the photon subtraction operation can be realized;when one port inputs the number state and the other port performs the vacuum state detection, the photon addition operation can be achieved.In addition, the combination of BS and conditional measurement can also realize the scissors of quantum state dimensions and prepare new nonclassical quantum states [23–29].
Actually, these above are about the applications of a BS.In these applications, the transformation relation of a BS is only used.But,the common transformation relationship cannot effectively lead to the normal ordering form for some complex combined operators.In order to realize this purpose, it is possible to appeal to different representation of operator.For instance,Jia et al gave the expression of the BS operator in the coordinate and momentum representations, which reveals many kinds of decomposition for a BS operator[30],enriching the theory of the BS operator and deepening the understanding of the operator.Moreover, the combination between the BS operator (Gaussian operator) and annihilation operator (non-Gaussian operator) is often encountered in many researches.Usually, it will be convenient for further investigation by obtaining the normal ordering form.Note that the coherent state is the eigenstate of the photon annihilation operator,and it is also a kind of intermediary state between classical and quantum states.We propose the coherent state representation of the BS operator, and examine applications of the BS operator in the coherent state representation.Using the technique of integration within product of operator (IWOP), the representation of the BS operator is derived in the coherent state representation, which is further extended to two types of cascaded BS operators.Then considering the entangled state prepared by the coherent state and the coherent superposition state as the entanglement source, the quantum teleportation of the coherent state is discussed.
This paper is arranged as follows.Firstly, the coherent state representation and the normal ordering of the BS operator is introduced.The second part is some applications of the coherent state representation of the BS operator,mainly including finding the normal product of the mixed BS operator, and the BS operator is used to obtain a kind of quantum entangled state representation with a mixture of continuous variables and discrete variables.The third part introduces two kinds of models about cascade BSs: singlemode-shared and two-mode-shared cascade BSs, whose coherent state representations and normal ordering forms are derived.The forth part discusses the quantum teleportation of the coherent state using the output entangled resource when the coherent state and the superposition state are used as the input state of the BS.The last part is the conclusion.
2.Coherent state representation of a BS operator and its normal ordering form
Suppose that two input ports and two output ports of a BS correspond to photon annihilation operators a, b, c, d, satisfying relationship[a,a†]=[b,b†]=[c,c†]=[d,d†]=1,then the input–output relationship is given by
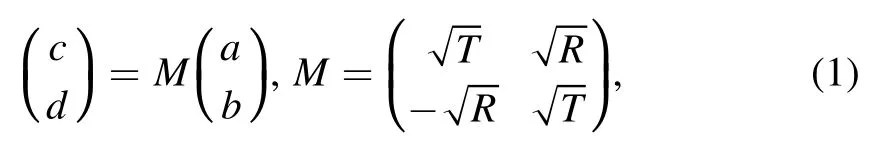
whereR= sin2θ,T=cos2θare the reflectance and transmission of the BS.
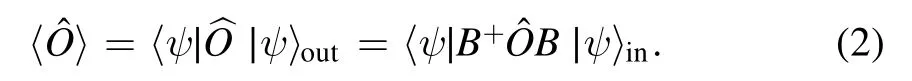
If considering the operatoras an input annihilation operator a, b, then in the Heisenberg picture, one can see

where : : is the normal ordering symbol, equation (7) can be derived as
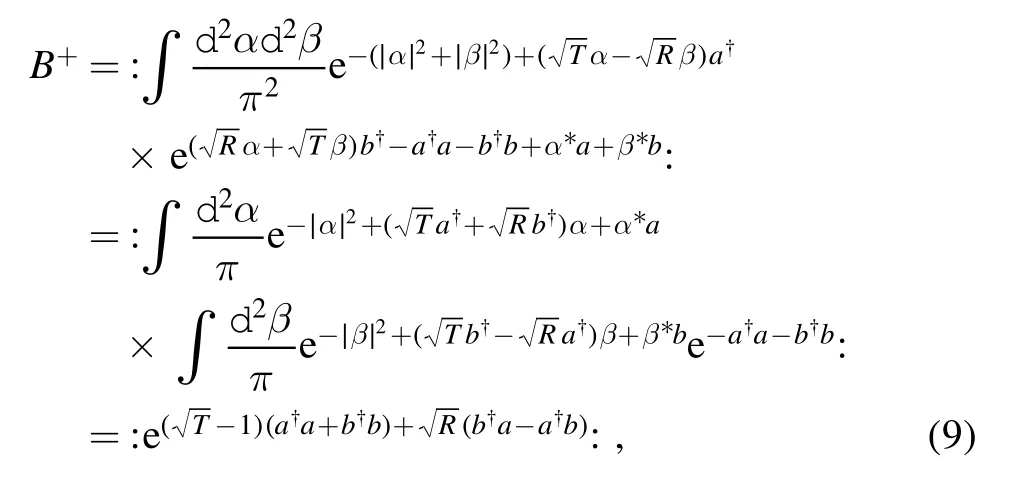
where the IWOP technique and the following integral formula

are used.Equation(9)is just the normal ordering form of the BS operator.It should be noted, when using the IWOP technique to integrate,the whole operator has to be within the normal ordering symbol.
Taking the Hermite conjugate of equation(9),we can get[30]
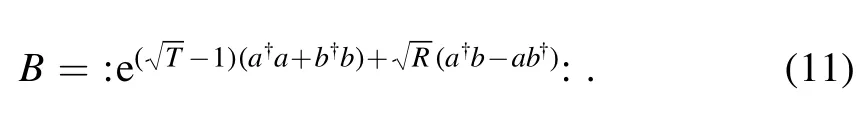
SubstitutingR= sin2θ,T=cos2θinto equation (11) and taking the derivative of the variable θ, we have
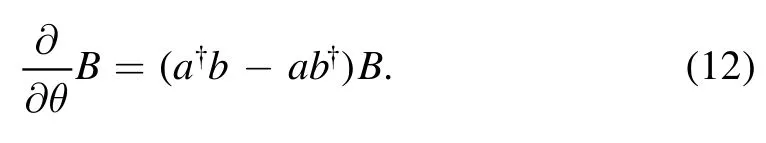
Thus, the exponential form of the BS operator is given by[30]

Here we present the coherent state representation of the BS operator.In this representation, it is direct to obtain the corresponding normal ordering form of the BS with the help of the IWOP technique.This is different from the conventional BS model only using the transformation relation.In addition, the method can be extended to derive the normal ordering form of other operators shown in next section.It is difficult for obtaining the normal ordering form via the conventional BS transformation relation.
3.Applications of a BS operator’s coherent state representation
Next, considering some applications of the coherent state representation of the BS operator, including the derivation of the normal ordering forms of both general operator and the mixed BS operator,and the application for the preparation of quantum mechanical representation.
3.1.Normal ordering forms of operators
Firstly, considering the normal ordering formof operator amBa†n.Using equation (7), we have
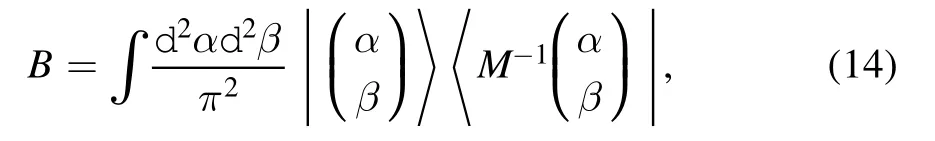
then, the operator amBa+ncan be directly expressed as

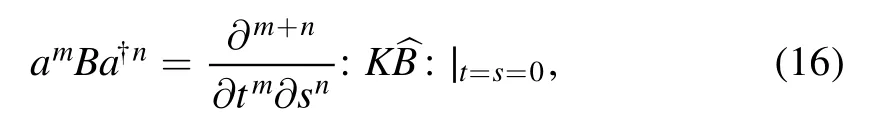
where

Using the differential definition formula of the bivariate Hermitian polynomial, i.e.,

then equation (16) becomes
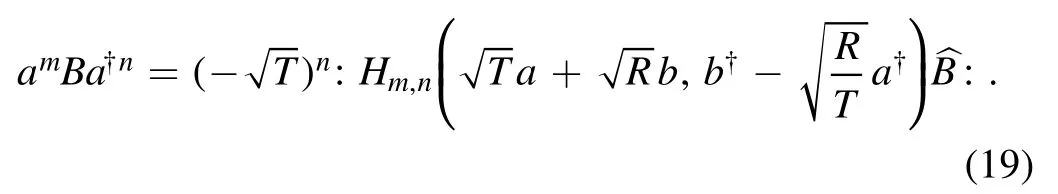
This is the normal ordering form of the operator amBa+n.It can be regarded as the product form of the bivariate Hermite polynomial and the BS operator within the normal ordering.Using equation(19),the matrix element〈m|B|n〉can be easily obtained



Noting the differential form of the bivariate Hermitian polynomial, we have

thus

as expected.
3.2.Preparation of entangled state representation
The BS can not only be used to prepare non-classical quantum states, such as the aforementioned Laguerre polynomial excited coherent states, but also to obtain quantum mechanical representations, such as entangled state representations.Here, the BS operator is going to be used to prepare a kind of quantum entangled state representation characteristic of mixing continuous variables and discrete variables.
Considering coherent state |z〉aand Fock state |n〉bas inputs of the BS.Using equation (11) and the coherent state representation in the Fock basis, i.e.,
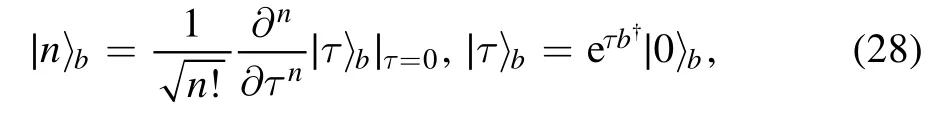
then the output entangled state can be obtained
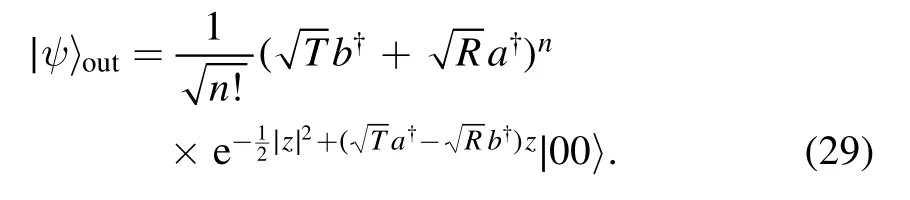
Equation (29) is just a kind of entangled state representation mixing continuous and discrete mixed variables.
In fact, using the IWOP technique, the completeness of∣ψ〉outcan be directly proved as

i.e.,

Here, in the derivation of equations (30), (8) and (10) are used.The completeness of equation(31)is just the reason that the entangled state∣ψ〉outis called the quantum mechanical representation.
On the other hand,using the representation equation(14)under the coherent state representation of the BS operator,the Schmidt decomposition of∣ψ〉out,i.e.,
Equation (31) is just an entangled state representation and equation (31) is the Schmidt decomposition showing the entanglement.
4.Coherent state representations and normal ordering form of two cascaded BS operators
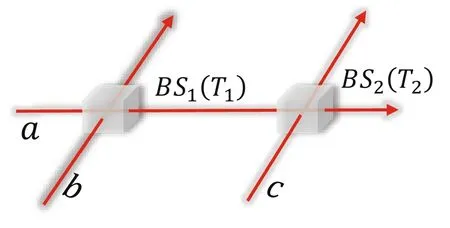
Figure 1.Single-mode-shared cascaded beam splitter (BS) model.
For two independent BSs, the normal ordering of their product can be given by equation (11), which is a direct generalization.Here, considering the case of two cascaded BSs,that is, the non-independent case.The action of two BSs has the characteristic of sequence, which is widely used in the construction of entangled states representation in multimode case and the preparation of non-classical quantum states as well as the measurement of quantum precision.
4.1.Single-mode-shared cascaded BS operator
First, considering the cascade of two optical BSs acting one after the other, as shown in figure 1.The two optical BS operators can be expressed as

the BSs acting on the input states, the total operator can be expressed as Babc=Bac(T2)Bab(T1).Using equation (33), we have

Using the IWOP technique and performing the integration over the variable α, we have

where we have set
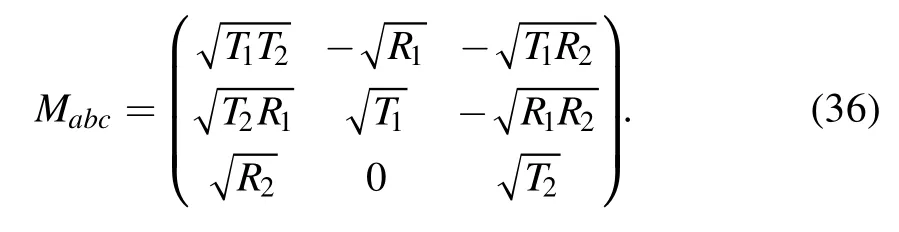
Equation (35) is the representation of the whole operator of the two single-mode-shared cascaded BSs (figure 1) in the coherent state representation.

Figure 2.Two-mode-shared cascaded beam splitter(BS)model.Top image: single phase shift case; Bottom image: two phase shift case.
Using the IWOP technique,integrating equation(35),the normal ordering form of the whole operator can be obtained
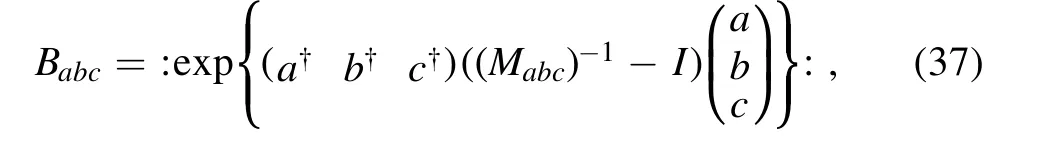
where (Mabc)-1is the inverse matrix of Mabc, i.e.,

Further using the operator identity formula [32, 33]

the exponential form of the cascaded BS operator in figure 1 is expressed as

4.2.Two-mode-shared cascaded BS operator (generalized Mach-Zehnder interferometer)
Next, considering the cascaded optical BS operator shown in figure 2, namely Mach–Zehnder interferometer.It is widely used in quantum precision measurement.Let the first and second BS transmittances be T1and T2, that is, considering the case of an asymmetric BS.The common Mach–Zehnder interferometer is a special case of the above example.
In figure 2, the up picture is the model of the interferometer undergoing a single-side phase rotation.The whole equivalent operator Bacan be expressed as
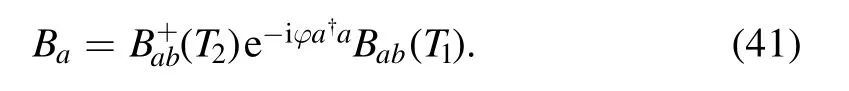
Using the coherent state representation of the BS operator,noticing that the normal ordering form of the phase operatoris

or

where|α〉is the coherent state,equation(41)can be rewritten as
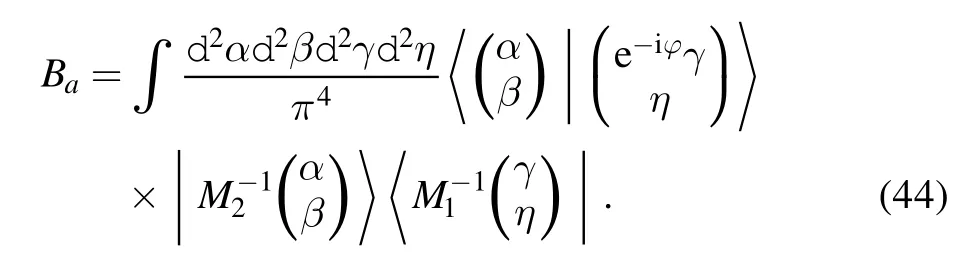
Using the IWOP technique, we have

In particular, when there is no phase shift inside the interferometer, namely, φ=0, T1=T2, then Ba=1, as expected.
Only when φ=0, for the two cascaded BSs with different transmittances, equation (45) becomes

where
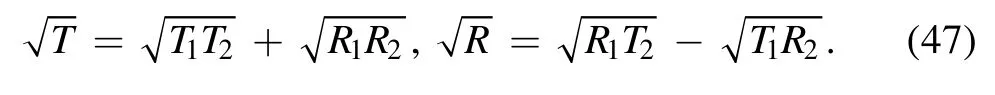
It can be seen from equation(46)that two BSs with different transmittances,cascaded in the manner shown in figure 2,are still equivalent to one BS,and its transmittance is determined by equation (47).
Only when T1=T2=1/2, equation (45) becomes
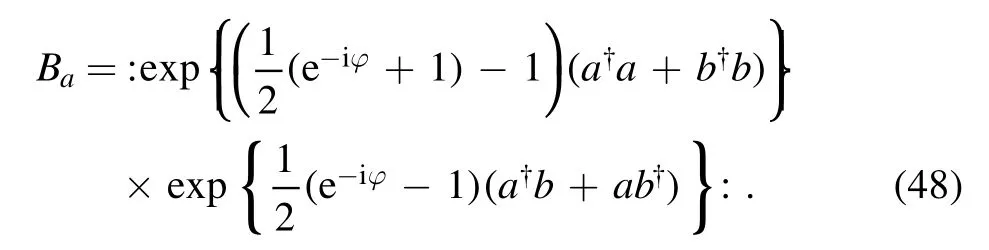
If the transmittance coefficient t and reflection coefficient r are taken as

satisfying |t|2+|r|2=1, then equation (48) can be shown as
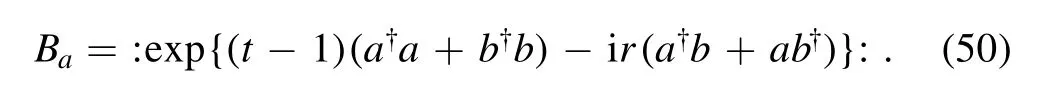
Equation (50) is a BS operator with complex transmittance parameter.At this time, the transmittance (complex number)of the BS is determined by the phase factor.
In figure 2, the down picture is the model of the interferometer undergoing two-side phase rotations.Similarly,the whole equivalent operator Ba+bcan be expressed as

i.e.,

When φ=0 or φ=0 and T1=T2,the above result is consistent with the previous result.Interestingly, only T1=T2=1/2,equation (52) becomes
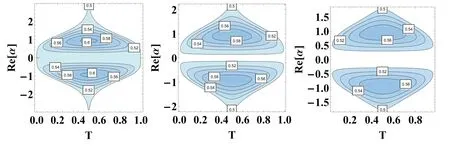
Figure 3.The difference function of two-dimensional contour map between the fidelity and the classical limit 1/2 as a function of coherence amplitude and transmittance.
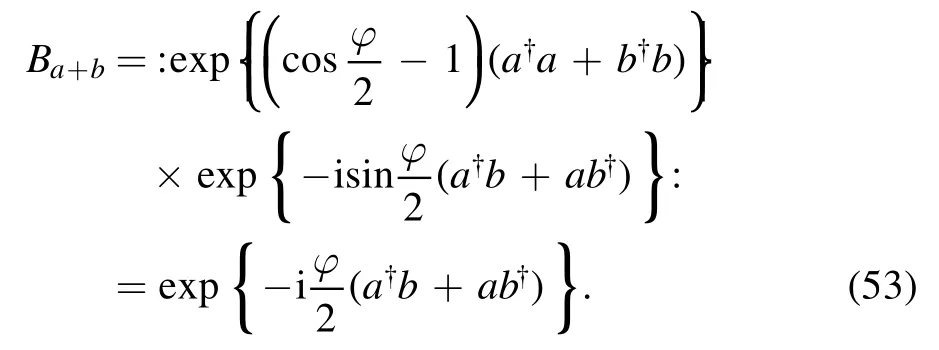
It can be seen that for the BS cascade model in figure 2, when T1=T2=1/2,the whole operator is still a BS operator.At this time,the transmittance(real number)of the BS is determined by the phase factor.
5.Application of the BS in quantum teleportation
In the last section, we consider a common application of an entangled state prepared by a BS.Although a BS can be used to prepare many entangled state representations characteristic of completeness relation, not all entangled state representations can be effectively used to achieve quantum teleportation.Here we only consider coherent state and superposition of coherent states as inputs to realize the preparation of entangled resource for realizing quantum teleportation of coherent state, and the ideal quantum teleportation scheme(Braunstein and Kimble (KB) scheme) [34].It is interesting that, in this scheme, when the coherent state is teleported the teleportation fidelity is independent of the coherent amplitude[35].Therefore, for the convenience of discussion, we only examine the teleportation of the vacuum state.
Using the anti-normal ordering form of the displaced operator and the completeness relationship of the coherent state representation,Jia et al derived a formula for calculating the teleportation fidelity [36], i.e.,
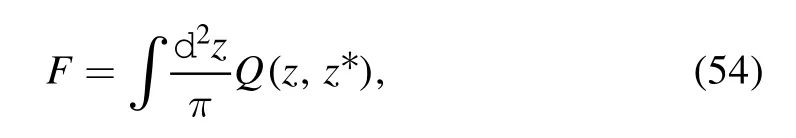
whereQ(z,z* ) = 〈z,z* ∣ρ12∣z,z* 〉is the Q function representation of the entanglement source ρ12.Therefore,when the Q-function of the entanglement source ρ12is known, then equation (54) can be used to calculate the teleportation fidelity.
Using the normal ordering equation (11) of the BS operator, we can get

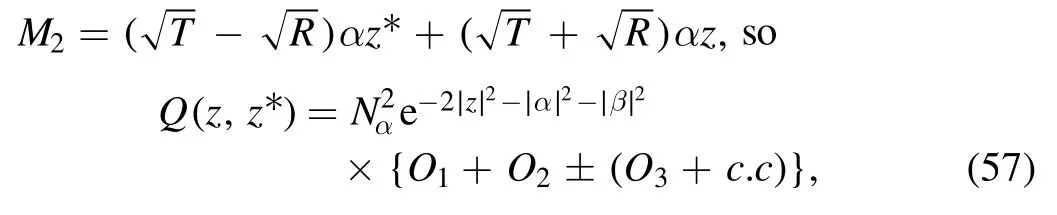
where

and
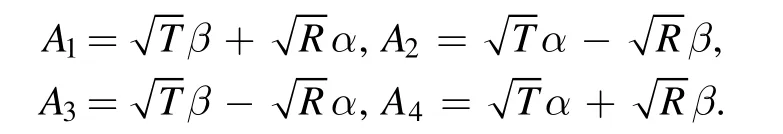
Substituting equations(57)into(54),and using equation(10),we can get

where

In order to clearly see the entanglement characteristics of the output state, that is, whether the teleportation fidelity exceeds the classical limit 1/2, figure 3 shows the difference function of two-dimensional contour map between the fidelity and the classical limit 1/2 as a function of coherence amplitude and transmittance.From left to right, β=0,0.1, 0.2.From figure 3, it can be seen that (i) when the coherent state and the cat state are input, there are two symmetric regions where the fidelity is greater than the classical limit; (ii) when the optical BS is symmetrical, the teleportation effect is the best; (iii) the amplitude of the coherent state increases so that the teleportation fidelity is lower, even lower than the classic limit case.
6.Conclusion
Using the input–output operator transformation relationship of the BS,the coherent state representation of the BS operator is introduced.Combining the IWOP technique,we derived its normal ordering form.Based on the coherent state representation of the BS operator,as applications,we derived some operator identities, and a class of quantum entangled state representations are obtained in which continuous variables and discrete variables are mixed.In addition, the normal ordering form of two kinds of cascaded BS operator and its tight exponent forms are further derived, including two single-mode-shared BSs and two two-mode-shared BSs.The latter is actually a kind of generalized Mach–Zehnder interferometer.This provides a direct and effective theoretical tool for the application of Mach–Zehnder interferometer in quantum precision measurement and other issues.
Finally, considering the coherent state and the superposition state as the inputs of the BS, and the output state as the entanglement source to realize the quantum teleportation of the coherent state.The effects of the BS transmittance and the coherent amplitude of the input state on the fidelity are discussed.The research method in this paper can be further extended to the nonlinear transformation process, and the related research results have good theoretical value in the fields of quantum optics and quantum information.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Grant Nos.11964013, 11664017), the Training Program for Academic and Technical Leaders of Major Disciplines in Jiangxi Province (20204BCJL22053).
ORCID iDs
杂志排行
Communications in Theoretical Physics的其它文章
- Dynamics of mixed lump-soliton for an extended (2+1)-dimensional asymmetric Nizhnik-Novikov-Veselov equation
- Entanglement witnesses of four-qubit tripartite separable quantum states*
- From wave-particle duality to wave-particlemixedness triality: an uncertainty approach
- Photon subtraction-based continuousvariable measurement-device-independent quantum key distribution with discrete modulation over a fiber-to-water channel
- Enhancement of feasibility of macroscopic quantum superposition state with the quantum Rabi-Stark model
- Precision measurements and tau neutrino physics in a future accelerator neutrino experiment
