Dynamics of mixed lump-soliton for an extended (2+1)-dimensional asymmetric Nizhnik-Novikov-Veselov equation
2022-03-23KaiZhongShiShouFengShenBoRenandWanLiWang
Kai-Zhong Shi, Shou-Feng Shen, Bo Ren and Wan-Li Wang
Department of Mathematics, Zhejiang University of Technology, Hangzhou 310014, China
Abstract A new (2+1)-dimensional higher-order extended asymmetric Nizhnik–Novikov–Veselov(eANNV)equation is proposed by introducing the additional bilinear terms to the usual ANNV equation.Based on the independent transformation,the bilinear form of the eANNV equation is constructed.The lump wave is guaranteed by introducing a positive constant term in the quadratic function.Meanwhile,different class solutions of the eANNV equation are obtained by mixing the quadratic function with the exponential functions.For the interaction between the lump wave and one-soliton, the energy of the lump wave and one-soliton can transfer to each other at different times.The interaction between a lump and two-soliton can be obtained only by eliminating the sixth-order bilinear term.The dynamics of these solutions are illustrated by selecting the specific parameters in three-dimensional, contour and density plots.
Keywords: Extended ANNV equation, Hirota bilinear method, lump solution
1.Introduction
In soliton theory, exact solutions of nonlinear partial differential equations(NPDEs)play an important role in predicting and understanding possible behaviors of physics phenomena.There are many powerful methods for solving soliton solutions of NPDEs, such as the inverse scattering transform method [1], the Darboux transformation [2, 3], the Hirota bilinear method [4, 5], the Lie group method [6] and so on[7–10].The dynamical characteristic of soliton solution is widely studied in fractional differential systems [11–13].
Recently, there has been a growing interest in a rational solution localized in all directions of spaces,which is called a lump wave.A lump wave can be widely applied to fluids[14, 15], nonlinear optics[16], plasma physics [17] and microwaves [18].Many methods are proposed for lump solutions, such as the Hirota bilinear method [19–26], the long wave limit method[27–29],the Darboux transformation[30] and the extended homoclinic test method [31].
The (2+1)-dimensional asymmetrical Nizhnik–Novikov–Veselov (ANNV) equation arises from a model for an incompressible fluid[32]where p and r are the components of the dimensionless velocity[33]in the ANNV equation.It was first proposed by using the weak Lax pair [34].Actually, the ANNV equation can also be obtained from the inner parameter-dependent symmetry constraint of the KP equation[35].The ANNV equation has important applications in incompressible fluids, including shallow-water waves with weakly nonlinear restoring forces, long internal waves in a densitystratified ocean and acoustic waves on a crystal lattice[36,37].
The rogue waves of the ANNV equation have grown in popularity as they represent surreptitious oversize sea waves[38–40].The phenomena of rogue waves can create huge water walls taller than 20-30 meters which cause extensive damage to ships, coastal oil platforms and marine industries [39].Sometimes these massive rogue waves will become Tsunamis, due to underwater disturbances such as earthquakes, volcanic eruptions, typically with the aid of a nuclear explosion or asteroids [41].The interaction between a lump wave and two soliton can be considered as a special rogue wave.The study of lump waves and the interaction between a lump and a soliton is a significant problem.In this paper, the lump solution and interaction between a lump and multi-kink soliton of the ANNV equation are studied by the Hirota bilinear method[36].
The ANNV equation reads as follows
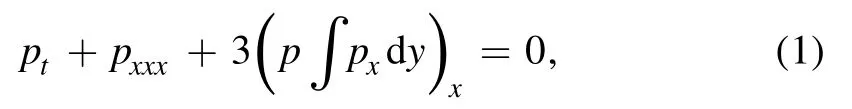
or

where p(x, y, t) is the evolution of wave surface function.Equation (1) or (2) could be considered as a model for an incompressible fluid.In fact, by the transformations r=uxand p=uy,the ANNV equation can transform to one variable ANNV equation

We can obtain the Hirota bilinear form of the ANNV equation(3)by using the transformationu= 2 (l nφ)xand the Hirota bilinear form reads as

In this paper, we focus on constructing a high-order NPDE by introducing the additional bilinear operators base on the ANNV equation.The lump solution and the interaction solutions of the ANNV equation are studied by using the Hirota bilinear method.The eANNV equation reads

where δi(i=1, 2, 3, 4) are arbitrary constants.While the arbitrary constants are δ1=δ2=δ3=δ4=0, (5) will become the usual ANNV equation (3).Rogue waves with higherorder terms are widely studied in [42–44].In contrast, lumps are rarely studied in the high-order nonlinear systems [45].This is the main motivation to extend the ANNV equation to a high-order nonlinear system and study the lumps and their interaction solutions of the eANNV equation.
This paper is organized as follows.In section 2, the Hirota bilinear form of the eANNV equation is obtained by using the dependent variable transformation.The lump solution is given by solving the Hirota bilinear form of the eANNV equation.In sections 3 and 4,the interaction between a lump and a soliton,and the interaction between a lump and two-soliton are obtained by adding an additional exponential or two exponential functions to a quadratic function.The last section contains the conclusion.
2.Lump solution of the eANNV equation
The eANNV equation (5) can be transformed to a Hirota bilinear equation

under the transformation

Equation (6) has the following bilinear form:

where Dx,Dtand Dyare the Hirota bilinear operators defined by

To search for a lump solution to the eANNV equation (5), we begin with a quadratic function solution as

where ai,(1 ≤i ≤9)are all real parameters to be determined.Substituting equation(10)into equation(6)and balancing the different powers of x,y and t yields the following constraining conditions on the parameters:

While φ is a class of positive quadratic function solution of equation (6), the constraint conditions should satisfy
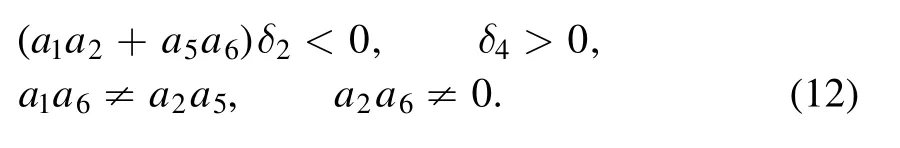
By substituting parameters (11) and equation (10) into transformation(7),we can obtain a class of lump solution for the eANNV equation (5)
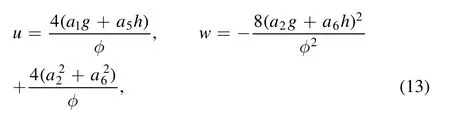
where

and a1, a2, a5, a6, δ2and δ4satisfying (12).The parameters are selected as
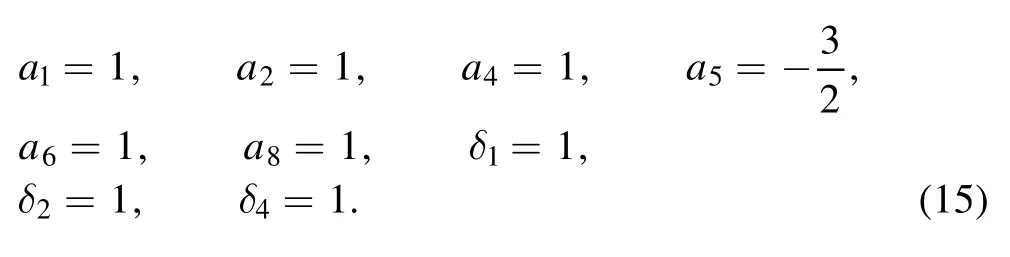
The solutions of u and w are shown in figure 1.The solutions of u and w are rationally localized in all directions of the spaces.The three-dimensional plots of the lump wave for u and w are presented in figures 1(a)and 1(c).We can explicitly see a localized characteristic of a lump solution with time t=0.It shows that the lump wave for u and w has one peak and one valley, one peak and two valleys, respectively.Figures 1(b) and 1(d) represent the density plot of the solutions u and w.

Figure 1.Profile of solutions u and w.Figures (a) and (c) are three-dimensional plots with time t=0, (b) and (d) are density plots with time t=0.
The critical points of the lump wave are solved

By solving the above condition(16),we find that the function u reaches the maximum and minimum values at

Explicitly,the above two critical points are symmetrical at the point

The function w reaches the maximum value at
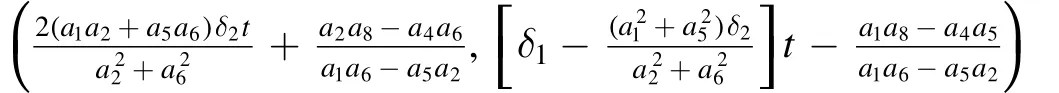
and the minimum values at two points
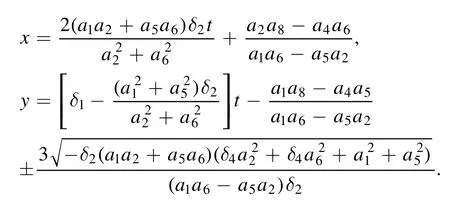
It can be found that two minimum points are symmetrical at the maximum point.The energy of the lump solution distributes in a small region (near these critical points).The parameters δ1, δ2and δ4can affect the location of critical points from the analysis above.
To catch the moving path of the lump wave in (13), the critical point of the lump wave is calculated by solving φx=φy=0.The exact moving path of the lump wave is written as

and the moving speed of the lump wave reads
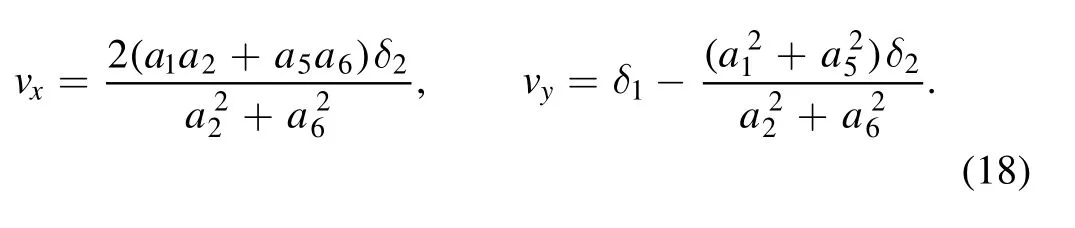
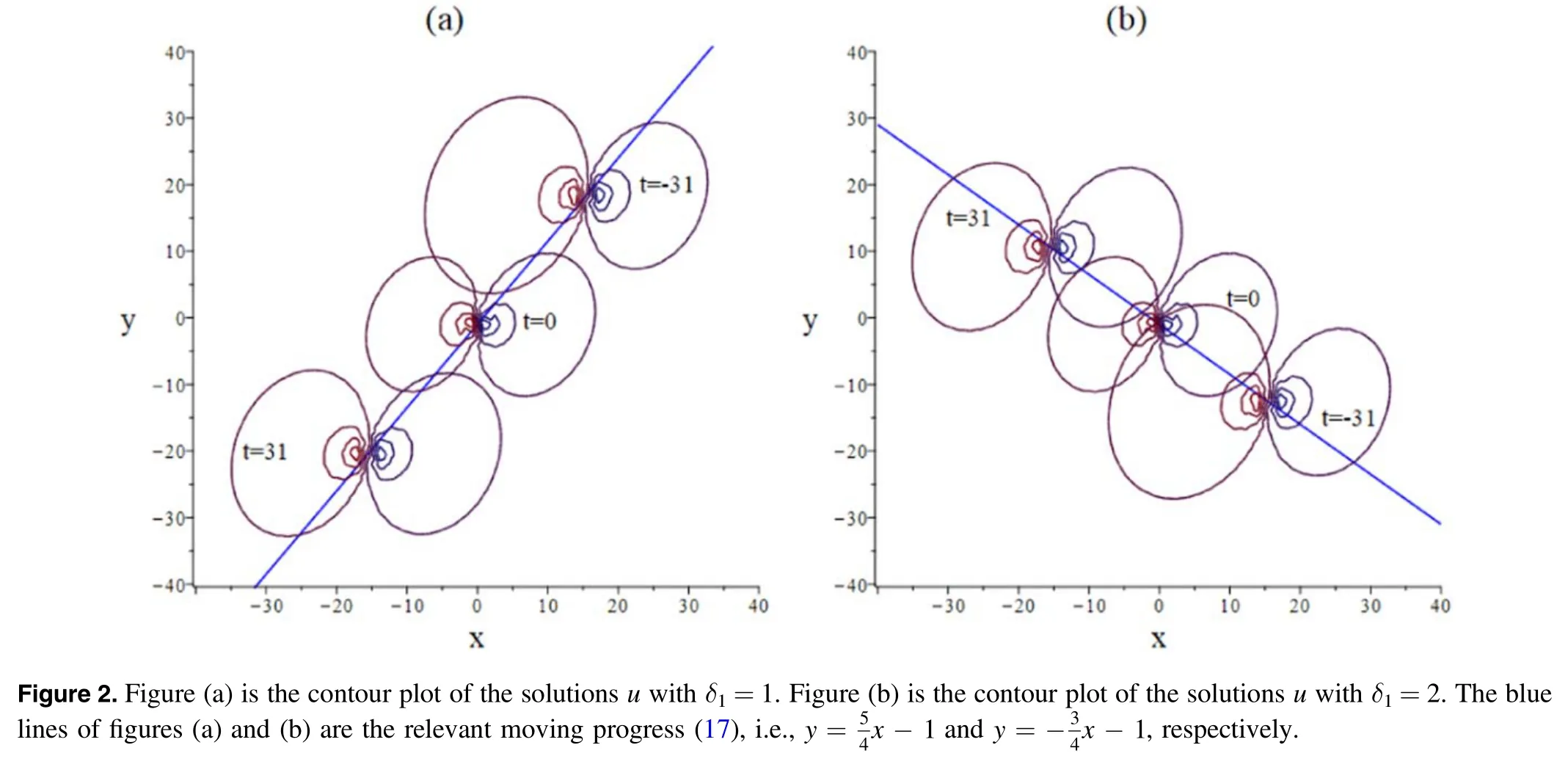
To explain the impact of new parameters on the lump wave,one must select δ1=1 and δ1=2 in figures 2(a)-(b), respectively.Other parameters are selected as (15).The contour plots of the lump wave are presented at t=-31,t=0,t=31.The blue lines of figures 2(a)and 2(b)are the relevant moving progress(17),i.e.,andrespectively.From figure 2, it can be found that the parameter δ1can control the moving path in(17) and the moving speed in (18) of the lump wave.
3.Interaction solution between a lump and a soliton
In order to obtain the interaction between a lump and a soliton of the eANNV equation (5), we need to rewrite the solution(10) as the following form:

where ki(1 ≤i ≤5) are five undetermined real parameters.Substituting equation (19) to equation (6) and balancing the different powers of x, y and t, we can obtain the following three cases of the parameters.
Case 1.
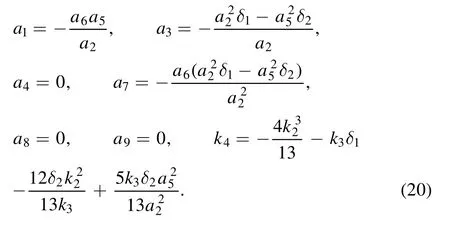
The parameters should satisfy the constraint conditions

and δ2, δ3and δ4are

In order to obtain the interaction solution of the eANNV equation(5),we substitute parameters (20)and equation(19)into transformation (7).The solution reads
where

The characteristics of the interaction solution with time t=-10,0,18 are shown in figure 3.The spatial structure of the interaction solution is described in figures 3(a) (c) (e).Figures 3(b)(d)(f)represent the corresponding density plot of the interaction solution.It is found that the lump wave and soliton wave are isolated at time t=-10.The effect of the kink-soliton becomes dominant status at time t=18.The interaction between the lump wave and soliton occurs around t=0.The amplitudes of the lump wave are equal at the maximum and minimum positions.The amplitude at the maximum point is larger than the minimum point for the kink-soliton.The amplitude of the lump wave in kink-soliton background is thus asymmetrical in figure 3(e).The energy of lump wave transforms to the kink-soliton with the time increase.
Case 2.
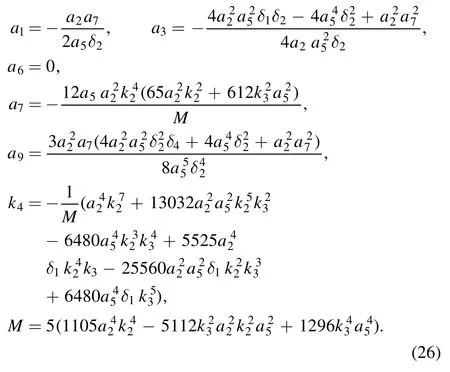
The parameters should satisfy the constraint conditions

and δ2, δ3and δ4are

By substituting the parameters (26) and equation (19) into transformation (7).The solution is


Figure 3.Profile of equation(25).Figures(a)(b)are three-dimensional and density plots with time t=-10,respectively.Figures(c)(d)are three-dimensional and density plots with time t=0, respectively.Figures (e) (f) are three-dimensional and density plots with time t=18,respectively.

Figure 4.Profile of equation (36).Figure (a) is three-dimensional plot with time t=0, (b) is the corresponding density plot.
where

Case 3.
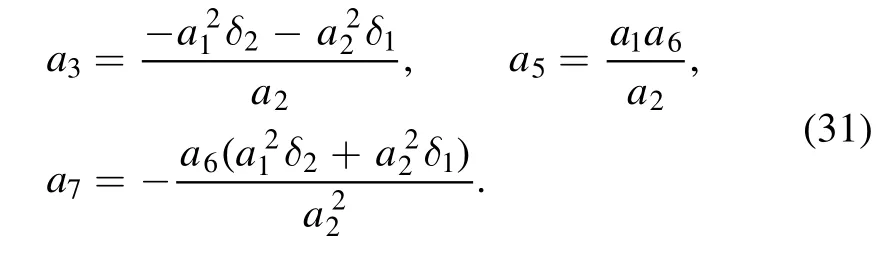
The parameters should satisfy the constraint conditions

and δ1, δ2, δ3and δ4are
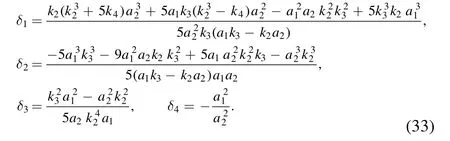
Similarly, we can get the interaction solution of the eANNV equation (5):
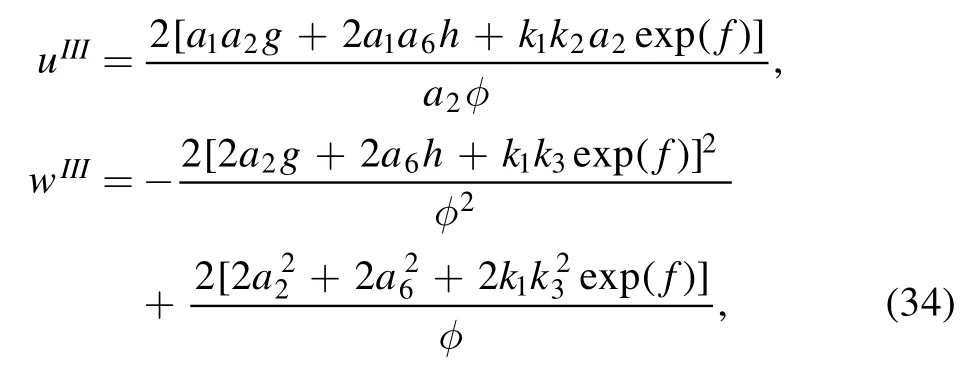
where

It is shown that the coefficients of x,y and t are the direct ratio for the square terms in (35).So it can not be given lump solution in case 3.
The selection of parameters are a1=1, a2=1, a3=1,a6=2, a8=2, a9=1, k1=1, k2=1, k3=2, k4=1 and k5=1.The rational solution reads

The spatial structure of the rational solution is described in figure 4(a).Figure 4(b) represents the corresponding density plot of the rational solution.
4.Interaction solution between a lump and two-Soliton
In this section, we will focus on the interaction between a lump and two-soliton.Similar to the interaction between a lump and a soliton, we introduce one additional exponential term, the new solution has the following form

where k6is a undetermined real parameter.By substituting equation (37) into equation (6) and vanishing the different powers of x, y and t, we can obtain the following set of constraining relations for the parameters

The parameters should satisfy the constraint conditions
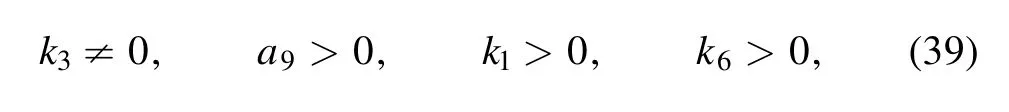
and δ2, δ3and δ4are
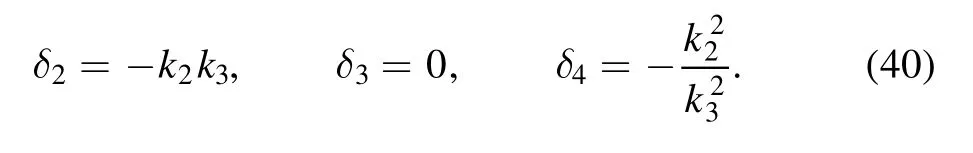
Through the analysis of constraint conditions,it shows we can obtain the interaction between a lump and two-soliton without the sixth-order bilinear term of equation (8).
By substituting parameters (38) into equation (37) and equation (7), a class of interaction solution reads

where

To illustrate the interaction solution, we select the following parameters
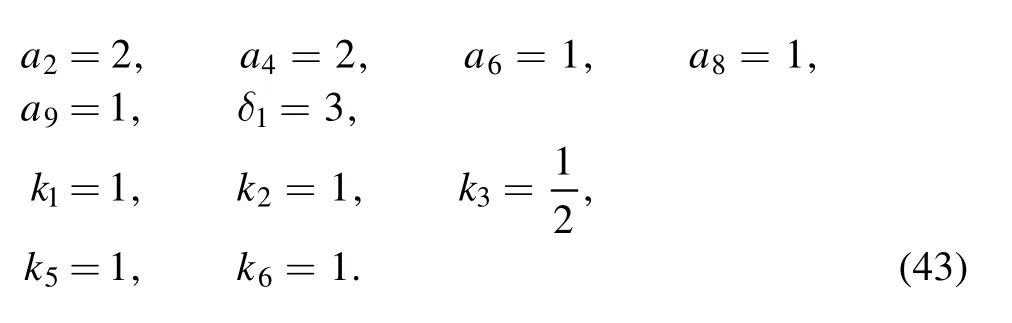
The interaction between a lump and two-soliton of u is presented in figures 5.Figures 5(a)-(d) present three-dimensional, density, contour and space-curved plots, respectively.The three-dimensional and density plots are presented with time t=0.From the contour plot, the moving path of the interaction wave is plotted explicitly with time t=-55, 0,55.The wave propagation pattern along the x-axis shows the different wave patterns by selecting time t=-20, t=0 and t=20.With time t ≈1.79 and the spatial coordinate x=0,y=0, a maximum value of u is around 5.22.The interaction solution w is plotted explicitly in figures 6(a) and 6(b).
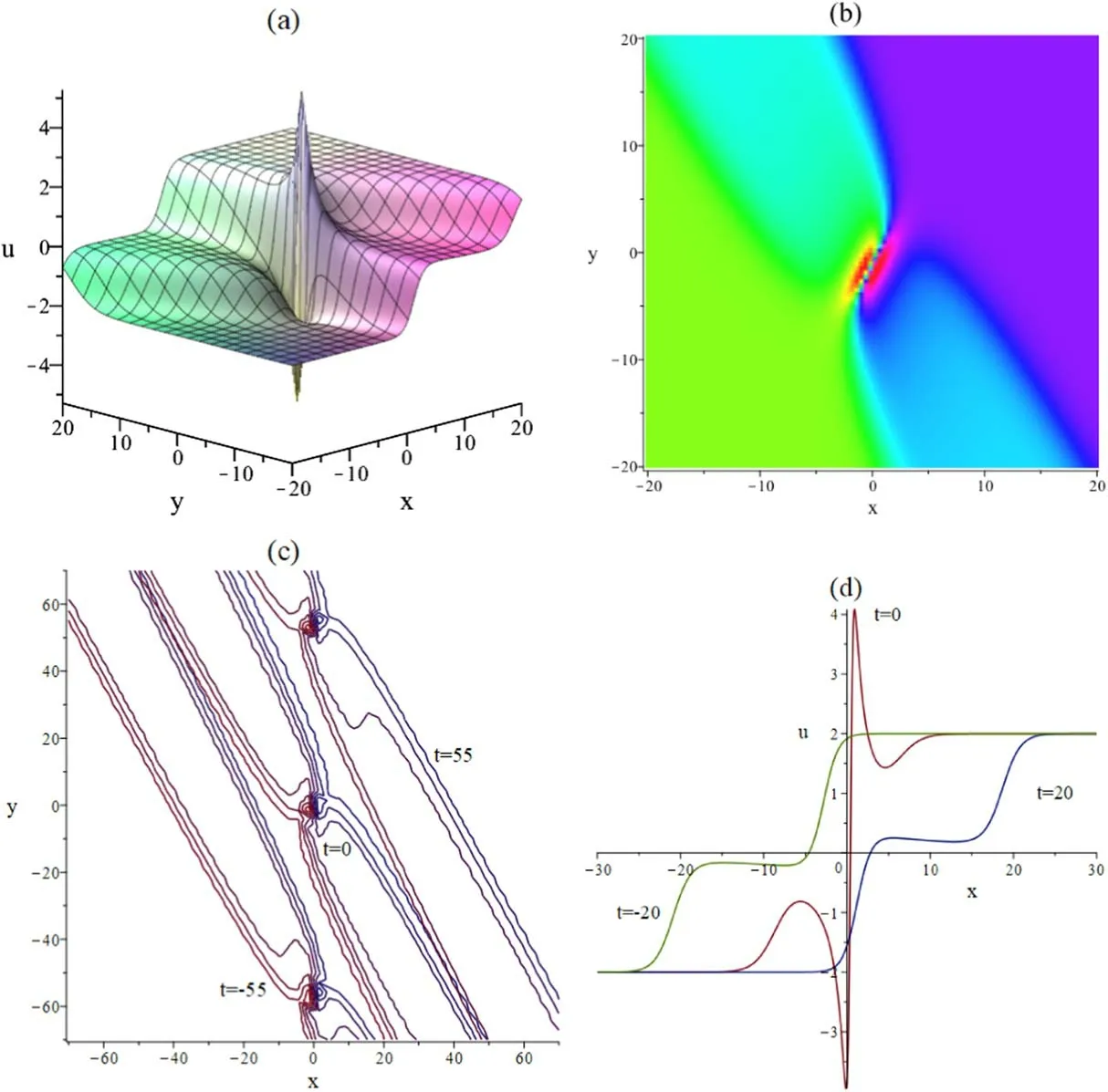
Figure 5.Profile of solutions u.Figure(a)is three-dimensional plot with time t=0,(b)is density plot with time t=0,(c)the contour plot shows the moving path with time t=-55, 0, 55, (d) the wave propagation pattern along the x-axis by selecting different times t=-20, 0, 20.
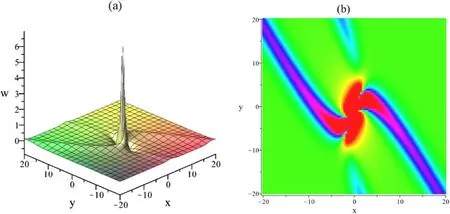
Figure 6.Profile of solutions w.Figure (a) is three-dimensional plot with time t=0, (b) is the corresponding density plot.
5.Conclusions
In this paper, we have presented a lump solution and interaction between a lump and multi-kink solitons of the(2+1)-dimensional eANNV equation by using the Maple symbolic computation.By introducing the additional bilinear terms,we obtain a new high-order nonlinear equation based on the ANNV equation.Through the Hirota bilinear method, we obtain a lump solution, two sets of interactions between a lump and a soliton, and an interaction between a lump and two-soliton solutions.By using graphical analysis, the lump wave is localized in all directions.In case I of the lumpsoliton solution,the effect of the lump wave is dominating at the negative time.The effect of the kink-soliton becomes large with the time increase.The energy of lump transforms to the kink-soliton in this process.By analyzing the constraint conditions of the interaction between a lump and two-soliton,this type of solution can only be obtained by eliminating the sixth-order bilinear term.These types of solutions for u an w are presented by three-dimensional, density, contour and space-curved plots.These results can explain some nonlinear physical phenomena and have the potential in incompressible fluid.The solutions outlined for equation (5) are worthy of further study.
Acknowledgments
This work is supported by the National Natural Science Foundation of China Nos.11775146 and 12105243 and the Natural Science Foundation of Zhejiang Province of China Grant No.LQ22A050002.
杂志排行
Communications in Theoretical Physics的其它文章
- Representation of the coherent state for a beam splitter operator and its applications
- Entanglement witnesses of four-qubit tripartite separable quantum states*
- From wave-particle duality to wave-particlemixedness triality: an uncertainty approach
- Photon subtraction-based continuousvariable measurement-device-independent quantum key distribution with discrete modulation over a fiber-to-water channel
- Enhancement of feasibility of macroscopic quantum superposition state with the quantum Rabi-Stark model
- Precision measurements and tau neutrino physics in a future accelerator neutrino experiment
