论数形结合法在经济学课堂中的应用

吴松彬 杨茹梦

（深圳职业技术学院，广东 深圳 518000）

一、引言

2019 年以来，教育部先后公布23 所本科层次职业教育试点学校和4 所独立学院转设的本科层次职业学校，形成涉及16 个专业大类的80 个试点专业，2020年又对职业教育专业目录进行一体化修（制）订。其中，以《西方经济学》为基础课程的金融科技应用专业、金融管理、等职业教育专业成为金融类高等职业教育本科教育重点培养专业。因此讲好《西方经济学》课程是完善金融类职业本科教育标准、保证本科教育层次职业教育顺利开展的基础性工作。在学生素质提升方面，《西方经济学》是经济学院大一新生第一学期的必修课、核心课和启蒙课，且该课程的经济学基本思想、基本规律以及基本理论贯彻整个经济学学科。另外，这门课不仅是专升本考试、经济学类入学考试的必考科目，同时西方经济学理论还在生活中扮演重要角色，这说明《西方经济学》在国民经济中具有广泛应用空间。综上，《西方经济学》课程的重要性不言而喻，该课对学生形成经济学思维、运用经济学技能解决生活实际问题发挥至关重要的作用。

西方经济学建立在严格前提条件和严密推导过程之上。由于大一新生经济学基础知识较为缺乏，数学工具掌握还不完善，学生充分理解西方经济学基础知识还比较吃力。因此如何通过通俗易懂的方法淡化推导过程，使学生清楚认识各个知识点的来龙去脉、进一步提升学生对经济学理论的理解力是教师提升西方经济学教学能力的重要环节。“数形结合”方法是数学领域运用几何方法解决代数问题的重要方法，著名数学家华罗庚用“数无形时少直觉，形少数时难入微，数形结合百般好，隔离分家万事休”这首诗评价该方法，充分彰显“数形结合”方法在数学领域的重要作用。在经济学教学过程中，若充分运用“数形结合”的方法阐述讨论经济学概念及理论，则能够使本来抽象的经济学理论更加通俗易懂，进而提高学生对经济学的兴趣，最终培养学生应用经济学理论分析现实经济问题的能力。基于此，论文尝试运用“数形结合”的方法重新演绎经济学经典消费者理论中三个重要推论（需求曲线为什么是直线，经济变量富有弹性临界值为什么为1 以及运用弹性理论分析“谷贱伤农”的适用性），以期帮助学生更好理解经济学理论和提升学生的经济学理论应用能力。

二、数形结合方法在经济学教学的案例分析

数形结合思想在解决中学题目、培养学生数学逻辑思维方面发挥重要作用，目前较少文献关注数形结合方法在经济中的应用。现有研究主要集中在两个方向。第一，数形结合在数学里面的应用。第二是数形结合在经济学中的应用。马宁和李尧(2009)运用图像法分析了经济现象，其本质就是一种“数形结合”方法。杨美兰(2012)将函数图像法用于《经济生活》教学，探讨了环境库兹尼茨曲线、拉弗曲线等经济学重要知识。邢展硕(2019)展示了图像法在《经济数学基础》教学中的简洁性、直观性和形象性等优势，该结论与樊福印(2005)保持一致。杨有平(2017)帮助学生从《经济生活》这门课寻找数形结合的数学思想。以往研究多从应试的解题方式讲解图像法的应用，无法真正体验数形结合方法在《西方经济学》的具体应用，我们尝试以数形结合方法为研究对象，探讨其在经济学教学实践中的应用，重新演绎经济学经典消费者理论中三个重要推论（需求曲线为什么是直线，经济变量富有弹性临界值为什么为1 以及运用弹性理论分析“谷贱伤农”的适用性），以期帮助学生重构经济学思考逻辑和培养运用经济学基础理论解决现实生活实际问题的能力。

案例一：需求曲线为什么是直线？

在教授需求曲线时，经常假设消费者需求曲线为直线。善于思考的学生就想，如果需求曲线为直线，那为什么学术界称之为需求“曲线”呢？需求曲线究竟在什么情况下会成为直线呢？或者说需求曲线的根源是什么？实际上需求曲线一般为曲线，但是价格越高需求量下降的基本规律保持不变。但为什么需求曲线是直线呢？需求曲线究竟是假设还是计算而来呢？虽然该知识点是高级西方经济学的内容，但是适当讲解需求曲线的由来不仅有助于学生构建完善经济学理论系统，还能帮助学生梳理经济学理论的内在关联。事实上，求解需求曲线是通过计算如下一个优化问题得到，其经济解释是最大化单个理性人的效用：

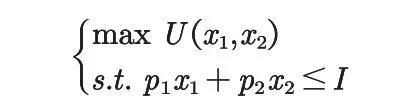
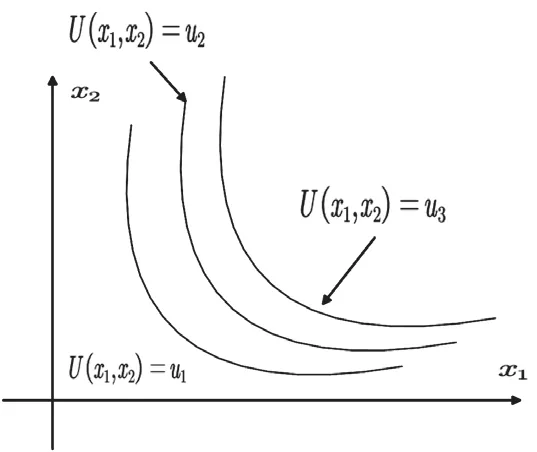
图1 无差异曲线图

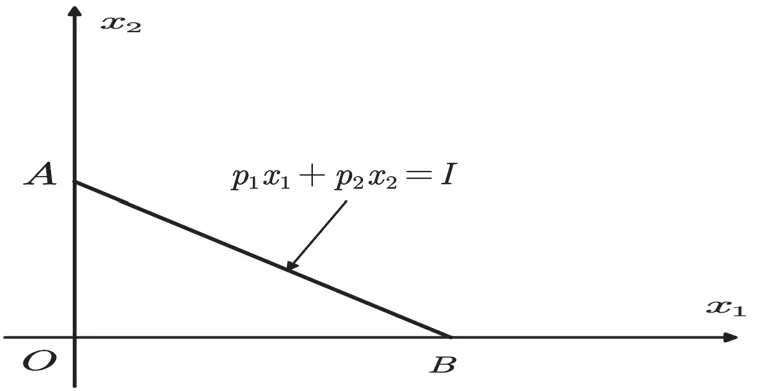
图2 消费者的预算约束曲线

图3 消费者需求曲线的由来

案例二：需求曲线倾斜度越高就越富有弹性吗？

弹性理论是消费者理论中的一个重要知识点。该概念由阿尔弗雷德·马歇尔提出，指一个变量相对于另一个变量发生一定比例的改变而改变的属性，简而言之可定义为一单位变量的变动带来另一个变量的变化量。其数学表达式如下：

很多学生初学弹性时，总会出现诸多不理解的地方，例如为什么要引入弹性。学生不理解弹性的根源在于学生未能准确明白弹性的经济意义及其应用。那么弹性这个概念究竟有何特殊之处呢？

1.弹性临界值为什么为1

弹性被定义为一个变量变动带来另一个变量的变动情况。该定义和弹簧的特性类似。弹簧弹性大，指的是用一个微小的力就可以带来较大的弹簧伸缩幅度，弹簧弹性小，指的是不管用多大的力，弹簧的伸缩幅度变化不大。借鉴上述含义，可以将弹性理解为一个变量与另一个变量变动的敏感程度。那么弹性又有哪些应用呢？以经典的需求价格弹性为例，需求价格弹性指的是价格带来需求量的变动情况，其定义为：

一旦提及弹性，学生均异口同声：如果需求价格弹性大于1，这意味着需求相较于价格而言富有弹性，若需求价格弹性小于1，这表明需求相较于价格而言缺乏弹性。一个被教师和学生忽略的问题是，为什么要以1 作为是否经济变量富有弹性的界限呢？现有教材并未有一致的答案。老师在上课的过程中也并未对其进行解释，只是灌输式的传授知识，如果弹性超过1，它的经济意义是指如果价格变化1%，需求量变化将会超过1%；如果弹性小于1，需求量的变化则小于1%。一个很关键的问题是，这个弹性临界值为什么是1，这个1 有什么特殊的经济意义吗？基于上述思考，论文将对该问题给予简要回答。回答上述问题不仅有利于帮助学生重新认识弹性的意义，同时还能通过弹性这个概念重新认识经济学理论中企业行为的本质——企业利润最大化。基于第一小节内容的分析，这里我们还是以需求价格弹性为例，假设消费者的需求价格曲线为直线，论文考虑如图4 中的消费者需求曲线，

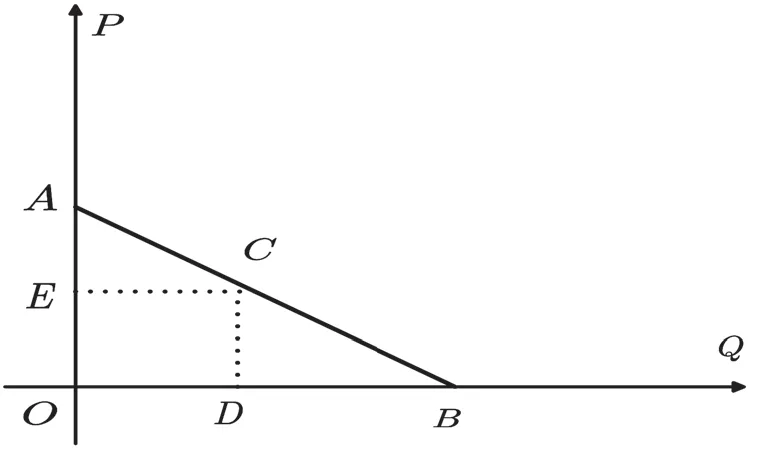
图4 消费者需求曲线的由来

值得注意的是，这里并没有将价格看成是产量的线性函数，也就是说在一般价格需求曲线下，上述推导结论也成立，即所得结论具有普适性。根据方程发现，如果要矩形EODC 面积最大，必然满足如下等式：

2.弹性的应用

经济学教材中常用需求价格弹性解释“谷贱伤农”。现有经济学老师对该现象的解释是，对于稻谷的消费者而言，其需求曲线较为陡峭，消费者对稻谷的需求价格弹性较高，由于稻农的整体收益由产量和价格共同决定。在此情况下，稻谷一单位的产量变化将会带来超过1 单位的价格变化，最终结局就是稻谷丰收反而会降低稻农整体收益，损害稻农的利益。上述解释存在两个问题，第一，需求价格弹性并不由需求曲线的陡峭程度单一决定，也就是说需求曲线陡峭并不能够直接说明需求价格弹性就越高。基于上述研究，任何需求曲线（只要与价格P 轴和产量Q 轴有交点）的需求价格弹性均在0 和正无穷之间，因此单从需求直线的陡峭程度并不能够直接判断弹性大小；第二，既然在同一条需求曲线上的需求价格弹性均在0 和正无穷之间，那么必然有某一个产量区间，在该区间内，需求价格弹性在0 和1 之间，即需求相对于价格而言缺乏弹性；而在其他区间，需求价格弹性在1 和正无穷之间，即需求相对于价格而言富有弹性。因此单纯从曲线的陡峭程度并不能够直接解释“谷贱伤农”这一现象。

现有学者主要从如下几个维度研究“谷贱伤农”现象。刘玲玲(2020)通过分析总产量和总产值之间的线性关系论证了我国不存在“谷贱伤农”现象。谷兰兰和苟强(2019)以2016 年高考真题为研究对象，探讨了不同坐标系下的需求曲线的倾斜程度并不能够说明谷贱伤农问题。孙小素(2006)从农产品缺乏弹性分析“谷贱伤农”的内在机理，并从经济学视角给出了促进农民增收路径。赵首军等(2011)基于“谷贱伤农”分析框架研究了内蒙古马铃薯滞销现象，并给出了建设性意见。综合现有文献，学者仅简单的画一条斜率较为陡峭的需求曲线，然后将其与供给曲线相交，通过平移供给曲线，主观认定斜率陡峭的需求曲线上，价格上升反而会带来生产者收益减少。

事实上，基于上述研究结论，“谷贱”不一定“伤农”，反而会“益农”。如图5 所示，稻谷产量整体在区间变动。当稻谷丰收时，此时若产量在范围内，随着产量Q 的提升，农民的收益的确会呈下降趋势，而当产量在OD 范围内，随着产量Q 的提升，农民的收益反而会呈上升趋势。因此基于弹性分析的视角并不能够解释“谷贱伤农”。那么“谷贱伤农”的根本原因到底是什么呢？回答上述问题必须全面考察观点提出者的经济思想及其所在的时代背景。

图5 需求价格弹性的变动图

“谷贱伤农，米贵伤民”出自《汉书·食货志上》，其作者为西汉的班固。在稻谷丰收时，土地所有者会故意压低稻谷价格，使价格处于较低水平，即图中的处于DB 之间，因而稻农的利润不增反降。土地所有者压价行为其实与经济学学家提倡的自由主义相违背。经济学领域强调稻谷产量上升，导致消费者的需求价格下降，只有当稻农的产量Q 处于图5 中DB 之间，稻农收益才会随着产量Q 的增加而下降，若稻农的产量Q在OD 之间，稻农的收益反而会随着产量Q 的增加而上升。因此用现阶段市场经济的需求价格弹性解释一千多年前“谷贱伤农”显然不合时宜。现如今中国水稻产量每年保持递增的趋势，但如果按照需求价格弹性理论，那现阶段中国水稻产量增长反而会伤害农民利益，农民种植水稻的积极性岂不是大打折扣？事实上，中国政府通过各种经济学手段（助农补贴、抬高收购价格等手段）保障稻农的利益，使得水稻的交易价格尽量在图中的C 点左右，即水稻增长反而会带来更多的收益。因此稻农种植水稻的积极性有增无减，当然稻农也会通过种植其他品种的农作物提升收入水平。

三、结论

大一学生学习理论性较强的西方经济学课程存在较大挑战。我们运用数形结合方法生动形象解释需求曲线的由来、为什么是直线以及弹性理论的应用。第一，对于解释需求曲线的由来，老师预设需求曲线为直线，忽视需求曲线存在的理论前提。运用数形结合的方法替代了拉格朗日求解最大化效用的方法，动态演绎需求曲线的由来及其为何为直线，使得学生更加清楚效用最大化、无差异曲线和需求曲线的内在联系，学生的经济学基础知识模块化、网络化、知识库化，学生的经济学思维以及逻辑思维能力进一步增强。第二，对于弹性理论的应用，运用数形结合的方法厘清运用弹性理论解释“谷贱伤农”的不合理性，并结合该观点的时代背景重新给出“谷贱伤农”的制度解释。第三，更为重要的是，基于弹性的定义，辨析了需求价格弹性并不是由曲线的斜率直接决定，还与某一点的位置相关，即并不是需求曲线越陡峭，弹性就越大。