基于高效遗传算法的电网需求侧调度优化研究及其收敛性分析

彭茜，王爱娟，李峻阳，刘万平

基于高效遗传算法的电网需求侧调度优化研究及其收敛性分析

彭茜，王爱娟，李峻阳，刘万平

(重庆理工大学计算机科学与工程学院，重庆 400054)

智能电网中大功率电器飙升及智能终端的普及，导致需求侧用电负荷增加所造成用电困难的问题。从分布式发电、市电以及居民用电三个角度考虑需求侧调度场景，并对其构建分时电价模型。随后，通过引入居民舒适度、用电经济度和负载方差三个衡量调度性能函数，构建出一种基于调度性能函数的加权优化目标模型。考虑到复杂多方的分时电价模型参与调度，提出了一种改进的遗传算法对需求侧进行用电调度来最小化目标函数。该算法通过加入精英选择策略和进化逆转操作，可有效地减少算法迭代次数，以取得目标函数最优值。然后，从理论上对所改进的遗传算法进行收敛性证明。最后，通过算例仿真验证了算法的有效性，并在满足居民用电舒适度的同时降低了31.29%的用电成本。

遗传算法；智能电网；分时电价模型；需求侧调度

0 引言

维持现代社会基础设施正常运行的底层是电力系统，从国防到交通、金融、日常生活都离不开电力系统的供应[1-2]。家用大功率电器数量的增加、智能终端和智能家电以及电动汽车的普及，导致居民用电比迅速增长[3]。为解决电力供应量需求过大问题，新能源发电和需求响应被提出[4]。为提高家庭能源利用效率，需求侧智能用电调度成为智能电网研究的热门[5]。用户侧进行主动用电调度优化对电网的运行和发展有重大意义[6]。为了便于更好地服务用户，提供更好的决策，以及针对不同用户的不同用电量需求问题进行了大量研究[7]。

为致力于电网更好地为用户服务，提出需求侧配合供给侧，可促使电网系统从垂直一体化向开放市场转变，实现更有效的供需平衡模式[8]。为了更好地解决需求侧调度问题，许多学者对此进行了研究。文献[9]考虑了较为简单的需求侧调度模型，仅考虑用户侧的用电器为可调度型和不可调度型，对可调度型用电器进行统一调度。在文献[9]的基础上，文献[10]考虑将储能设备加入到优化模型的需求侧调度中，但未对家用电器进行分类，并且也是对家用电器进行统一调度。随后，文献[11]将家用设备分为自动操作型与手动操作型，将自动操作型设备组合为能耗矩阵，但操作过于复杂。假设用户没有某一个用电器，则只能将能耗矩阵中用电器的对应元素进行删除，而用户多了某个用电器也只能在能耗矩阵中添加其对应元素；需要对每个用户进行不同的操作，考虑的模型不具有普适性。文献[9-11]只是将需求侧考虑为用户用电器类型的划分。为得到更加完善的用电模型，考虑在需求侧加入分布式发电模型，其中分布式发电模型可通过自主发电来供应用户的部分需求，可更好地利用资源。接着文献[12]考虑了分布式发电模型的接入，但未对家用电器进行分类，同样也仅对家用电器进行统一调度。在分布式发电加入后可能存在满足用户需求后还有剩余电量的情况，于是考虑市电模型接入。市电模型在满足用户需求后剩余电量可传入电网供应商以获取收益。在分布式发电模型、市电模型的基础上，文献[13]考虑到某些家用电器对用户影响程度较大，随意调度可能影响居民舒适度。于是将家用电器分为可调度用电器及不可调度用电器。在上述基础上，文献[14]提出需求侧用电器可中断负荷模型，更好地对家用电器进行调度，且增加了需求侧弹性。文献[12-14]考虑市电模型、分布式模型的接入以及对家用电器进行分类，降低了用户的用电费用，但是并没有考虑用户舒适度，而且会出现新的用电高峰及低谷的现象。

因此，依据上述讨论，本文将参考需求侧调度的多种分时电价模型(包含分布式发电模型、市电模型和居民用电负荷模型)，并引入三个指标函数衡量调度性能如下：

(1) 用户舒适度，调度后居民舒适度情况；

(2) 用电经济度，调度后节省的经济度值；

(3) 负载方差，为避免产生新的用电高峰。

根据以上背景可知，需求侧经济调度问题属于复杂优化问题，普通算法难以求解。进化算法中遗传算法[15](Genetic Algorithm, GA)是由教授John H. Holland提出的自适应全局搜索算法，可更好地解决复杂优化问题。文献[16]采用普通遗传算法对用电设备进行优化，但其调度性能不佳，其用电经济性和用户舒适性低。另外，普通遗传算法具有自身固有的缺陷：结果容易陷入局部最小值，收敛速度慢等。随后文献[17]提出一种改进遗传算法(G-DSM)对智能电网需求侧进行调度。与普通遗传算法相比，此算法基于锦标赛的选择和二元变异，在效率上有所提高。但是文献[16-18]对所改进的遗传算法并没有进行收敛性的理论证明，并且仅适用于简单模型的需求侧调度。

以上述研究工作为基础，结合分时电价背景，本文主要贡献如下：

(1) 从分布式发电、市电以及居民用电角度考虑需求侧调度问题，并对其构建分时电价模型。通过引入居民舒适度、用电经济度和负载方差三个衡量调度性能函数，构建出一种基于调度函数的加权优化目标模型。

(2) 基于轮盘赌选择、二元变异以及增加精英选择策略和进化逆转操作，提出了一种改进的遗传算法解决上述所构建的优化目标模型。相比于普通遗传算法，其算法时间效率高且求解结果更优。

(3) 从理论上对所提出算法进行了收敛性证明，通过实验仿真结果验证了所提算法的有效性，并通过与普通遗传算法对比，结果显示了此算法的高性能。

1 用户侧电力负荷建模

研究智能电网家庭负荷调度时，根据负荷特性划分为分布式电源模型、市电模型、居民用电负荷模型。

1.1 分布式发电模型

(1) 风能发电模型

风能发电机组的输出功率受到风速的影响，功率与风速关系的近似表达式为[19]

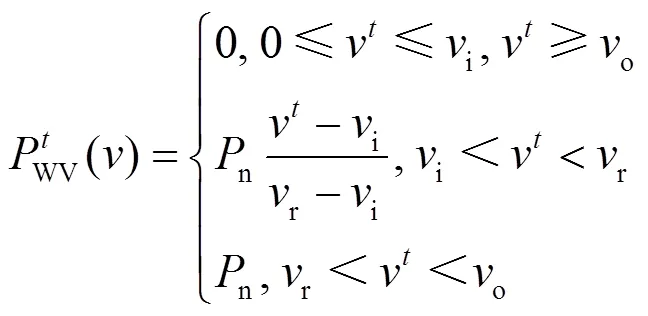
(2) 光伏发电模型

光伏发电由当时光照、外界温度及温度系数决定[19]。

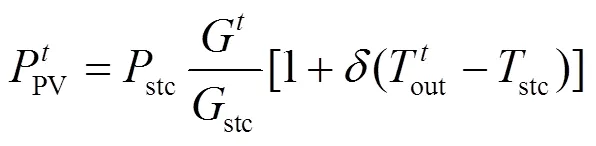
1.2 市电模型

考虑用户侧可与智能电网系统实现双向互动，当用户侧发电量在满足自身使用的同时还有富足时，将电量传给电网并获得相应收益，如式(3)所示。

当分布式发电量不足以满足使用时，向电网进行购买的公式为

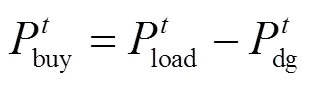
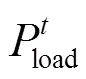
1.3 居民用电负荷模型

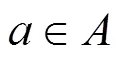
(1) 可中断型设备

需求侧调度时主要通过在负荷高时暂停可中断电器的使用数量，以达到减少负荷[16]。可中断负荷如式(5)。

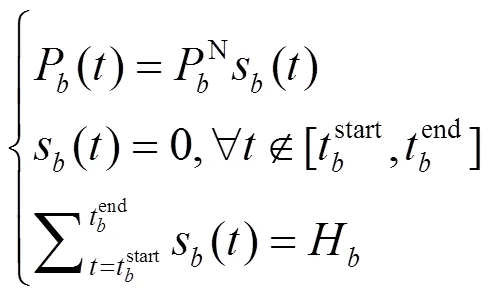
(2) 不可中断型设备

某些用电器中断影响用户使用，考虑不可中断负荷在开始运行直到完成才停止。

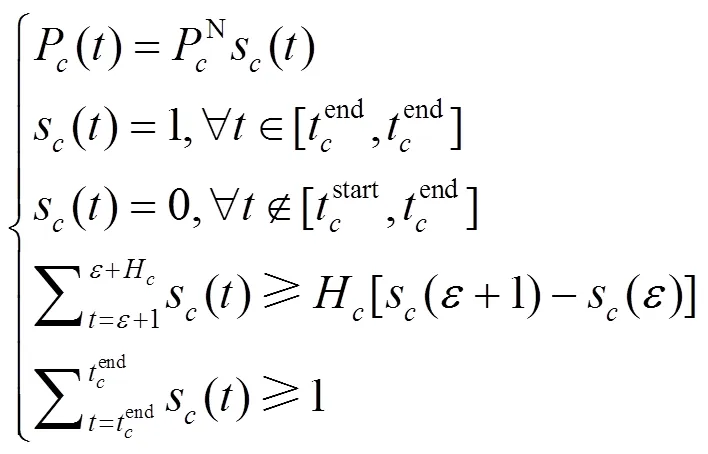
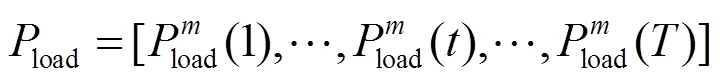
2 智能调度性能指标

为更好地降低用电费用，很多调度是将大量电器用电时间调到晚上，这样会影响用户的正常生活。为减少对电器的过度调度产生的影响，本文引入舒适度、经济度以及负载方差三个函数作为指标来评价调度结果，使优化后的负荷分布最优。

2.1 用户舒适度函数

对可调度型负荷调度时需要考虑用户的舒适度，即在分时电价下用户对改变后电器状态的接受程度。以下是对可调度电器的调度后舒适度值的描述。

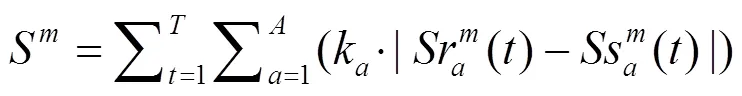
2.2 用电经济度函数

采用经济度函数是对用电成本进行评价，通过比较用电成本优化前后的差异[20]。采用经济度函数为

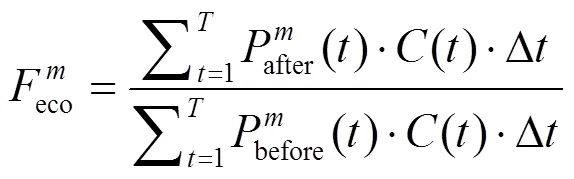
2.3 负载方差函数

在分时电价下，只考虑舒适度和经济性的优化方式会导致负荷转移到电价较低的时段运行，形成新的用电高峰[21]。所以为了降低用电高峰与用电低谷之间的差距，采用负载方差函数来进行约束，其函数为

2.4 目标函数

居民侧用电系统的优化目标是找出优化模型中全局最优解，使得用户的经济度和舒适度都得到满足，并降低电网负载的波动。然而不同用户对经济度和舒适度的偏好程度不同，本文利用加权的方式构建出用户用电的优化目标。

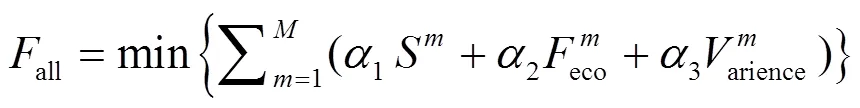
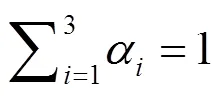
2.5 约束条件

(1) 功率限制约束

每种分布式电源输出功率处于一个最大值和最小值的约束区间，如式(14)、式(15)所示。

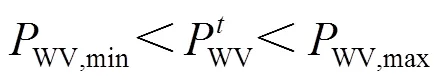
(2) 交互功率约束

电网在优化调度过程中，应该满足线性容量约束，销售和购买电力都必须满足式(16)、式(17)。

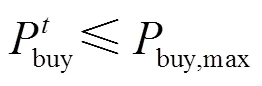
(3) 功率平衡约束

考虑电网买卖电量、风力发电电量、光伏发电电量之和满足用户当时的使用电量。

3 智能用电调度优化算法

优化算法主要是对居民用电模型进行调度。利用调度性能指标函数，评价调度的结果优劣。调度结果与分布式发电模型结合得出市电模型结果。

3.1 改进的遗传算法

遗传算法作为经典的优化算法，通常用于解决各类优化问题。针对本文优化目标模型，普通的遗传算法并不适用，并且普通遗传算法本身具有容易陷入局部最优，不一定能收敛到全局最优的缺点。基于以上的讨论，本文提出一种改进的高效能遗传算法。主要有以下改进。

(1) 选择操作，通过轮盘赌选择算法选择90%染色体。保留了优秀个体，也给差个体一部分生存空间避免陷入局部最优。

(2) 交叉操作，生成随机数与交叉概率比较。符合条件进行交叉操作。

(3) 变异操作，生成随机数与变异概率比较。符合条件进行变异操作。

(4) 进化逆转操作，具体操作过程为在之前进行交叉操作与变异操作的基础上，生成两个随机数，将两个随机数之间基因进行逆转(随机数相等则不做操作)，计算进化后各染色体的适应度，结果更优则更新染色体。

(5) 精英选择操作，对适应度排序，选取10%插入到种群。在迭代过程中保证种群数量与初始种群的染色体个数一样。

3.2 改进遗传算法的收敛性证明

对算法收敛性证明主要参考文献[22]，考虑遗传算法与马尔科夫链的相似性，遗传算法中每一次迭代仅与当前代染色体有关，与初始状态无关，可看出遗传算法与马尔科夫链定义类似，将遗传算法转换为马尔科夫链，进而对遗传算法收敛性进行证明。

假设将目标函数归纳为

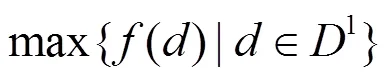
选择概率函数为

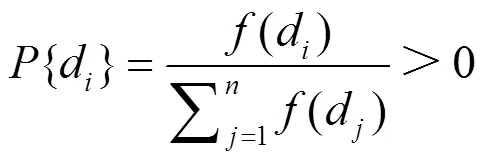
设变异概率函数为

为证明算法的收敛性，现引入以下引理。

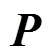
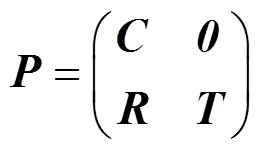
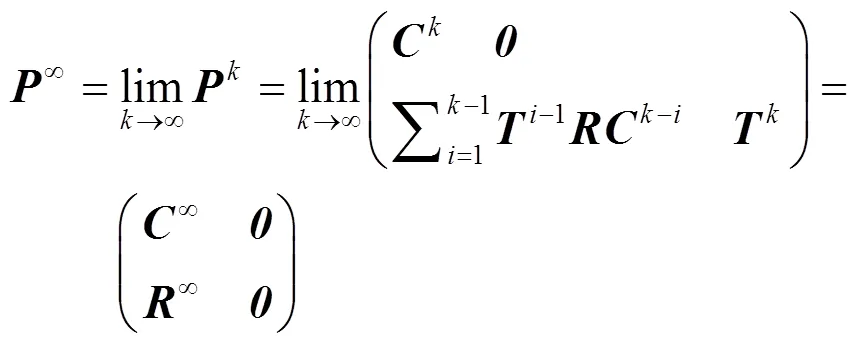
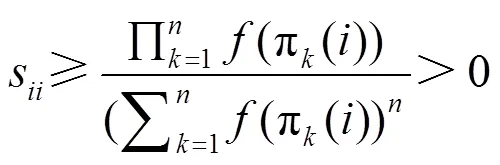
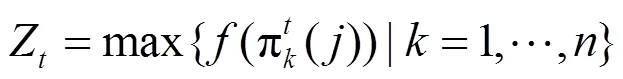
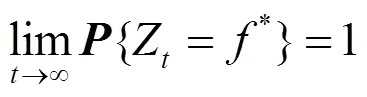
由以上定理及定义得出。

推论1：普通遗传算法不会收敛到全局最优。

定理 4：添加精英选择个体种群会保证每次保留更优值。

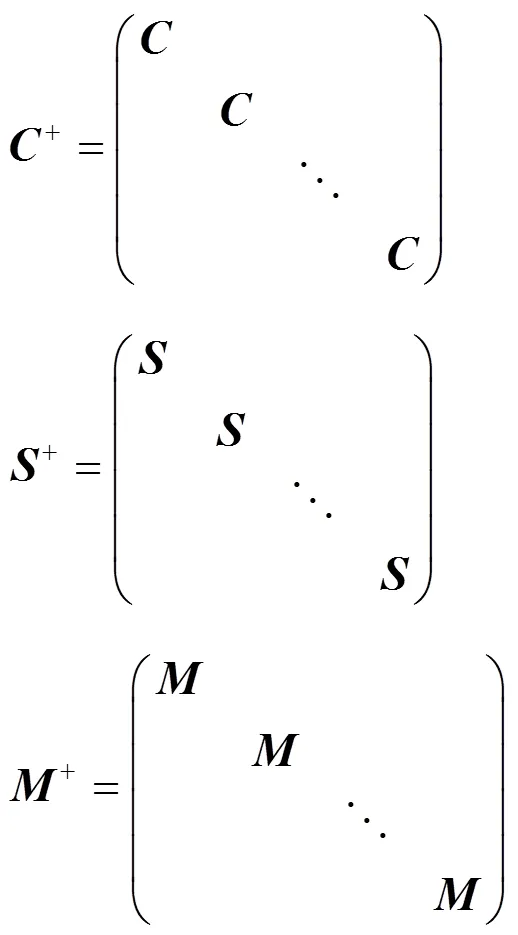
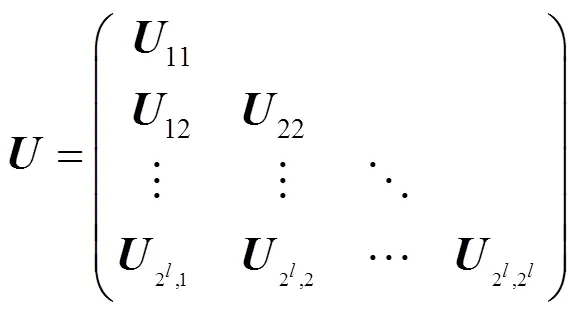
添加进化逆转操作选择种群个体进行进化逆转操作，计算适应度值，适应度值增加则保留个体，否则保留进化逆转操作前个体。可以保证种群每次保留更优个体。

推论2：提出的改进遗传算法，可收敛到优化目标(19)的全局最优解。

4 算例仿真

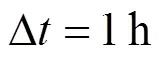
本仿真考虑日常13类用电器进行调度，其具体参数及可调用时间如表1所示。

根据表1中数据，计算每种电器在总功率中所占的比重，决定式(9)中参数的取值。计算单个电器所用功率占总用电器中的比值。依次确定算例仿真中值大小。具体得到的值如表2所示。

表1 家用电器参数表

表2 用电器权值参数表

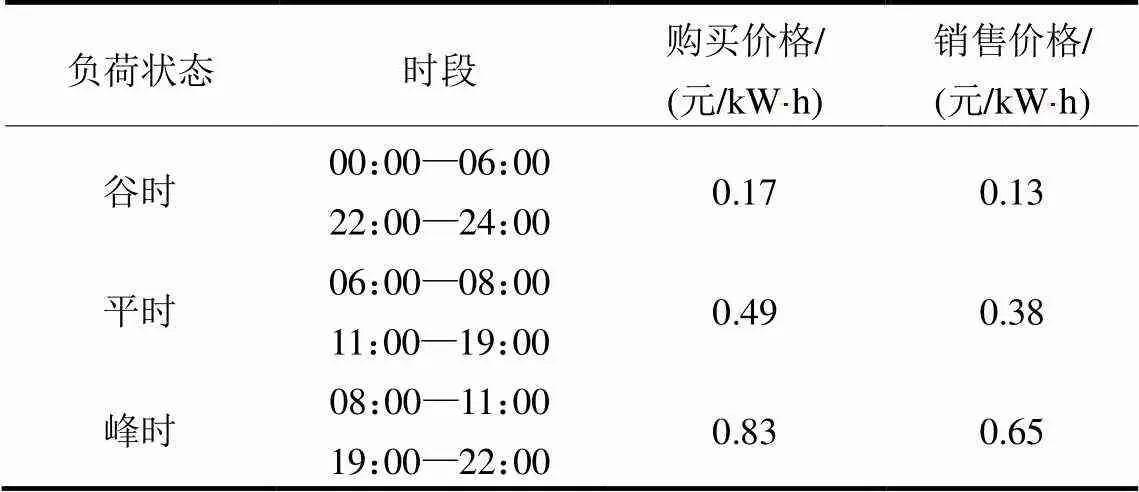
表3 分时电价参数表

分布式发电模型为光伏发电及风能发电，不消耗燃料且不会对环境造成污染，输出功率具有随机性及不可控性，分布式发电取每个时间段的最大输出功率发电。分布式发电量数据参考文献[25]，分布式发电每日发电功率见图1。

从图1可以看到，光伏发电时间集中于每天的中午，风力发电在一天时间中发电量较为平均。

居民负荷分为固定负荷及可调度负荷，固定负荷随意调度将影响用户日常的正常生活。因此对固定负荷不做调度，如图2。从图2中可看出可调度负荷比固定负荷使用量大很多，所以主要考虑对可调度的用电器进行调度，既可以减少用电成本，又能保证用户的舒适度。

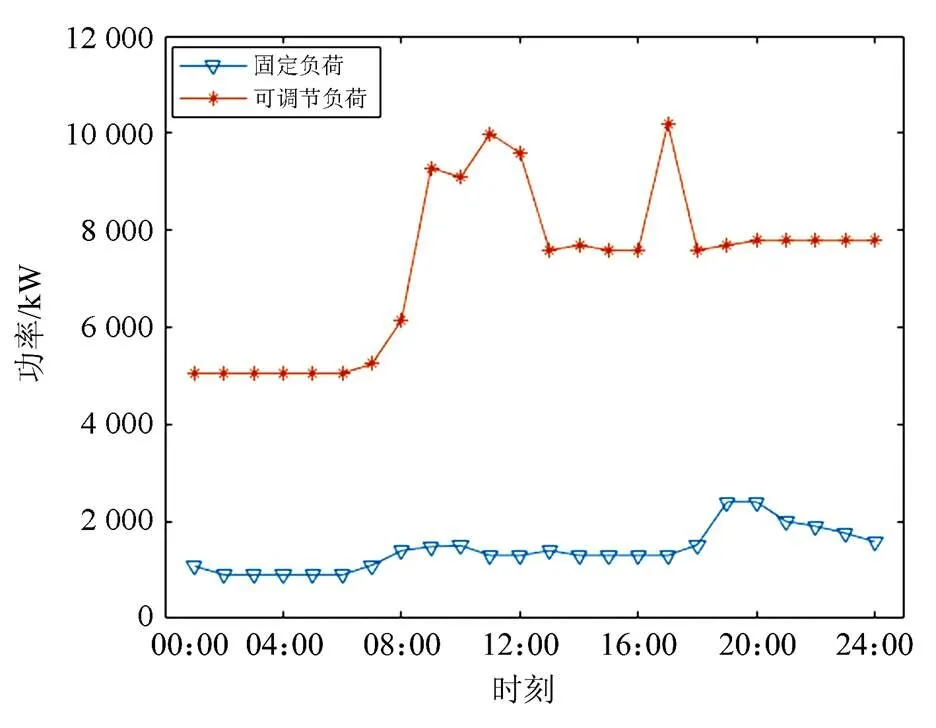
图2 可调度负荷与固定负荷

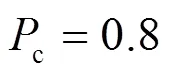
从图3可以看出，优化前家用电器使用时段主要为09：00—12：00和16：00，此时段为用电高峰。由于高峰期对电量的需求过大，对电网的要求也更高。普通遗传算法有效减少了高电价期间的用电量，但也导致出现新的用电高峰(如07：00—08：00)，用电低谷(如00：00—03：00、11：00—12：00、16：00、20：00)在调度时没有考虑用户舒适度及负载方差。改进后的遗传算法相对于普通遗传算法更加平稳，减少了用电量的同时也有效降低了峰谷差。

图3 优化前后对比电量使用对比图

同时，本文对两者的负载方差和用户经济度进行分析，负载方差是衡量用户用电量使用情况的聚集程度，主要为减少用电时段的峰谷差距。用户经济度是量化优化前后的用电成本对比，主要为减少用电成本。结果见表4。

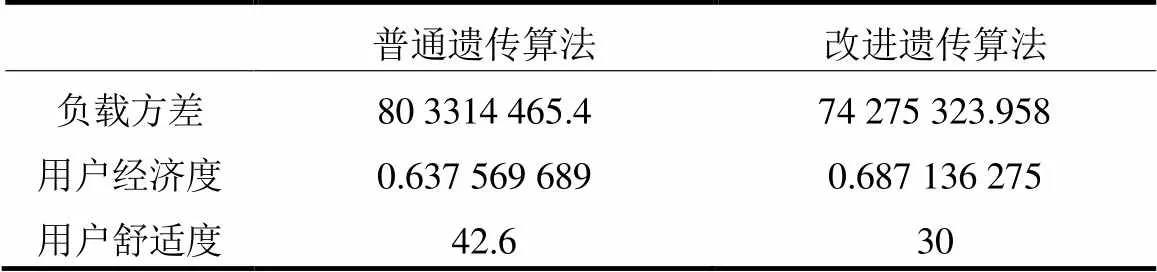
表4 算法效率对比

从上述结果可看出：

(1) 改进遗传算法可以更好地对用电器进行调度，黑色线走势相对平稳。且在用电高峰时段(08：00—13：00，16：00—19：00)都保持调度后用电量比之前更少，降低高峰用电问题。

(2) 在保证用户舒适度的同时，改进后的电价仅为调度前电价的68.71%。这在减少用户用电量的同时，也保证了用户的日常生活舒适度。

(3) 通过表4可看出，改进遗传算法的负载方差是普通遗传算法的0.092%。在用户经济度方面，普通遗传算法结果较好，但是普通算法存在很多不合理调度点，如11：00—12：00以及16：00应该是电量较多的时间，但是用电量却被调度到接近0，这显然是不合理的。

图4中纵坐标为每一次迭代过程中目标函数取值，改进遗传算法迭代速度较快，至40代左右基本收敛。但是普通遗传算法直到85代接近收敛。同时算法迭代结束得到各用电器在各时段的用电情况如图5所示。

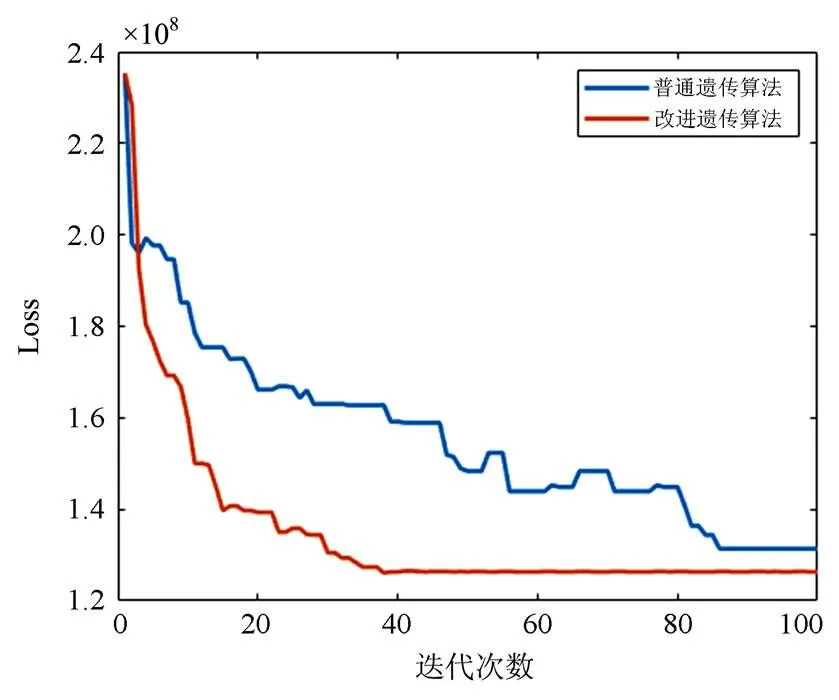
图4 收敛情况对比图

图5 各用电器的用电情况曲线

另外，考虑到市电模型的接入，本文对小区3 000住户进行仿真，考虑小区接入分布式发电模型后的用电过程，在用户用电时先使用分布式发电供应，当分布式发电供应不足以满足用户需求时，向电网购买电量进行补充。当分布式发电满足用户使用还有剩余时，可销售到电网获取利润。以下是市电模型仿真，图6为用户侧与智能电网能量流动情况，图7为最终交易价格曲线。

图6为用户侧与智能电网能量流动情况，其中负荷代表调度后小区用户的用电量。交换功率大于0，代表可以传输到电网的多余功率；交换功率小于0，则代表需要从电网得到的功率。

由图7可以看到，通过市电模型小区每日可得到收益为8 487.423元，可减少31.29%的支出。

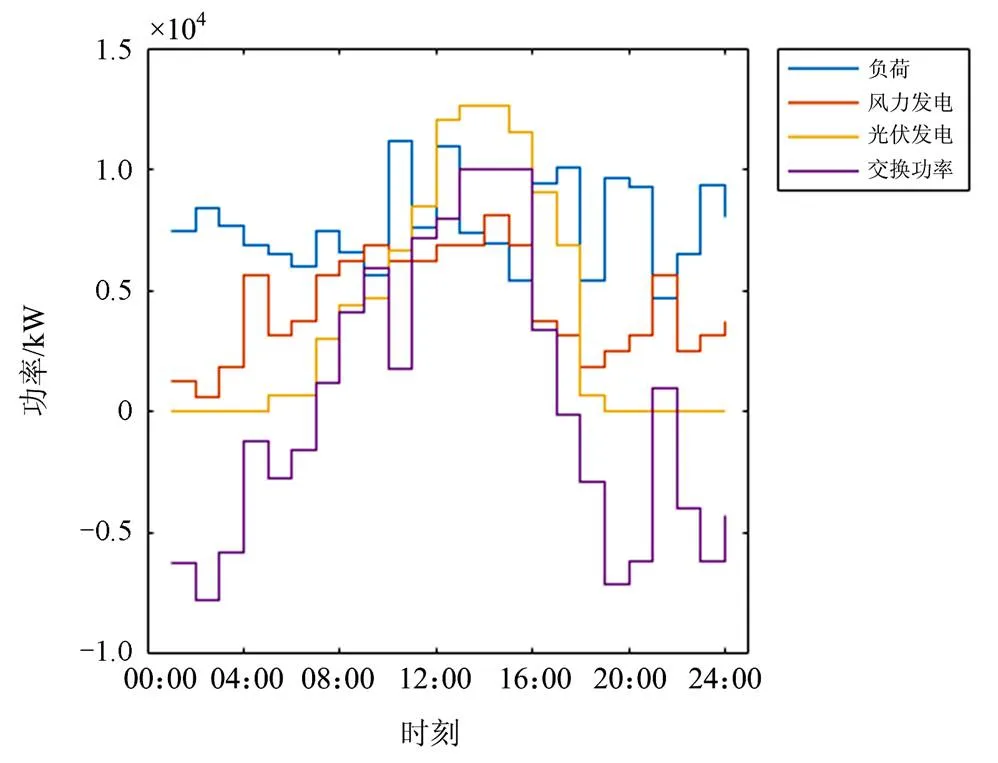
图6 用户侧与智能电网能量流动情况

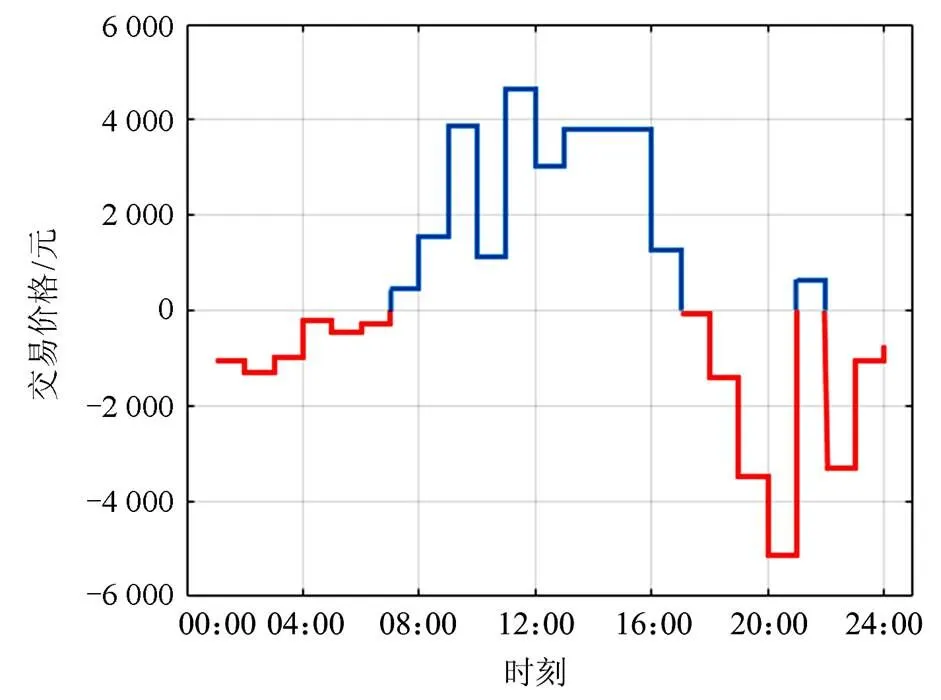
图7 交易价格曲线

5 结论

本文以用户负荷在分时电价下参与需求侧调度为背景，以家用电器类别为依据，考虑复杂多方的分时电价模型。随后通过引入用电经济度、用户舒适度和负载方差三个衡量调度性能函数，构建了一种基于调度性能函数的加权优化目标模型。最后提出一种改进的遗传算法来解决此优化问题，并对所提出的算法进行收敛性证明。通过研究得到如下结论：

(1) 本文提出的改进后的遗传算法与普通遗传算法相比，能够很好地避免陷入局部最优，造成新的用电高峰出现，找出更优解。

(2) 优化调度后在保证用电舒适度的情况下有效减少用电成本。某小区3 000户住宅经调度后一天的用电费用降低了31.29%。

(3) 降低电网的负荷波动，优化后的负载方差占优化前的0.092%，优化后的电网稳定性得到提高。

[1] YANG Xiaodong, ZHANG Youbing, HE Haibo, et al. Real-time demand side management for a microgrid considering uncertainties[J]. IEEE Transactions on Smart Grid, 2019, 10(3): 3401-3414.

[2] 杨晓东, 张有兵, 赵波, 等. 供需两侧协同优化的电动汽车充放电自动需求响应方法[J]. 中国电机工程学报, 2017, 37(1): 120-130.

YANG Xiaodong, ZHANG Youbing, ZHAO Bo, et al. Electric vehicle charging and discharging automatic demand response method based on collaborative optimization on both sides of supply and demand[J]. Proceedings of the CSEE, 2017, 37(1): 120-130.

[3] 杨波, 王琼, 杨仕博. 面向智能电网的文本分类研究综述[J]. 电子技术与软件工程, 2020(17): 198-200.

YANG Bo, WANG Qiong, YANG Shibo. A survey of research on text classification for smart grid[J]. Electronic Technology and Software Engineering, 2020(17): 198-200.

[4] 曹军威, 万宇鑫, 涂国煜, 等. 智能电网信息系统体系结构研究[J]. 计算机学报, 2013, 36(1): 143-167.

CAO Junwei, WAN Yuxin, TU Guoyu, et al. Research on smart grid information system architecture[J]. Chinese Journal of Computers, 2013, 36(1): 143-167.

[5] 杨博宇, 陈仕军. 电力负荷预测研究综述及预测分析[J]. 四川电力技术, 2018, 41(3): 56-60, 91.

YANG Boyu, CHEN Shijun. Overview and forecast analysis of power load forecasting research[J]. Sichuan Electric Power Technology, 2018, 41(3): 56-60, 91.

[6] 严道波, 文劲宇, 杜治, 等. 2021年得州大停电事故分析及其对电网规划管理的启示[J]. 电力系统保护与控制, 2021, 49(9): 121-128.

YAN Daobo, WEN Jinyu, DU Zhi, et al. Analysis of Texas blackout in 2021 and its enlightenment to power grid planning and management[J]. Power System Protection and Control, 2021, 49(9): 121-128.

[7] 白浩, 袁智勇, 周长城, 等. 计及新能源波动与相关性的配电网最大供电能力调度方法[J]. 电力系统保护与控制, 2021, 49(8): 66-73.

BAI Hao, YUAN Zhiyong, ZHOU Changcheng, et al. Dispatching method of maximum power supply capacity of distribution network considering new energy fluctuation and correlation[J]. Power System Protection and Control, 2021, 49(8): 66-73.

[8] 伍也凡, 刘浩田, 肖振锋, 等. 考虑源-网-荷不确定性的增量配电网规划研究综述[J]. 电力系统保护与控制, 2021, 49(8): 177-187.

WU Yefan, LIU Haotian, XIAO Zhenfeng, et al. Research review of incremental distribution network planning considering source-grid-load uncertainty[J]. Power System Protection and Control, 2021, 49(8): 177-187.

[9] 徐辉, 张会林, 叶玉凤, 等. 智能电网下用户用电系统多目标调度策略研究[J]. 电子测量技术, 2017, 40(7): 20-25.

XU Hui, ZHANG Huilin, YE Yufeng, et al. Research on multi-objective dispatching strategy of consumer power system in smart grid[J]. Electronic Measurement Technology, 2017, 40(7): 20-25.

[10]方逸波, 袁晓冬, 费骏韬, 等. 基于需求侧响应的配电网储能容量识别[J]. 电力工程技术, 2019, 38(6): 61-68.

FANG Yibo, YUAN Xiaodong, FEI Juntao, et al. Distribution network energy storage capacity identification based on demand-side response[J]. Electric Power Engineering Technology, 2019, 38(6): 61-68.

[11]秦超, 刘传清, 陈龙, 等. 基于价格博弈的需求侧管理智能控制系统研究[J]. 电气自动化, 2017, 39(3): 23-25, 29.

QIN Chao, LIU Chuanqing, CHEN Long, et al. Research on demand-side management intelligent control system based on price game[J]. Electrical Automation, 2017, 39(3): 23-25, 29.

[12]杨明, 王元超, 向东, 等. 智能电网中的家庭用电系统建模与优化分析[J]. 电力需求侧管理, 2017, 19(4): 6-10.

YANG Ming, WANG Yuanchao, XIANG Dong, et al. Modeling and optimization analysis of household power system in smart grid[J]. Power Demand Side Management, 2017, 19(4): 6-10.

[13]张延宇, 曾鹏, 臧传治. 智能电网环境下家庭能源管理系统优化调度算法[J]. 电力系统保护与控制, 2016, 44(2): 18-26.

ZHANG Yanyu, ZENG Peng, ZANG Chuanzhi. Optimal dispatching algorithm of household energy management system in smart grid environment[J]. Power System Protection and Control, 2016, 44(2): 18-26.

[14]朱兰, 周雪莹, 唐陇军, 等. 计及可中断负荷的微电网多目标优化运行[J]. 电网技术, 2017, 41(6): 1847-1854.

ZHU Lan, ZHOU Xueying, TANG Longjun, et al. Multi- objective optimization operation of microgrid considering interruptible load[J]. Power System Technology, 2017, 41(6): 1847-1854.

[15] HOLLAND J H. Genetic algorithms[J]. Scientific American, 1992, 267(1): 66-73.

[16]史林军, 史江峰, 杨启航, 等. 基于分时电价的家庭智能用电设备的运行优化[J]. 电力系统保护与控制, 2018, 46(24): 88-95.

SHI Linjun, SHI Jiangfeng, YANG Qihang, et al. Operation optimization of home smart electrical equipment based on time-of-use electricity price[J]. Power System Protection and Control, 2018, 46(24): 88-95.

[17]吴海伟, 王晓忠, 朱法顺. 一种基于遗传算法的智能电网调度方法[J]. 计算机与现代化, 2020(9): 122-126.

WU Haiwei, WANG Xiaozhong, ZHU Fashun. A smart grid dispatching method based on genetic algorithm[J]. Computer and Modernization, 2020(9): 122-126.

[18]陈刚, 区允杰, 孙景涛, 等. 基于改进遗传算法的含VSC-MTDC交直流混联系统最优无功潮流计算方法[J]. 广东电力, 2020, 33(12): 132-140.

CHEN Gang, QU Yunjie, SUN Jingtao, et al. Optimal reactive power flow calculation method for AC/DC hybrid system containing VSC-MTDC based on improved genetic algorithm[J]. Guangdong Electric Power, 2020, 33(12): 132-140.

[19]闫占新, 刘俊勇, 许立雄, 等. 风能等效转化利用模型及其效益研究[J]. 电力自动化设备, 2017, 37(6): 48-54.

YAN Zhanxin, LIU Junyong, XU Lixiong, et al. Research on the equivalent conversion and utilization model of wind energy and its benefits[J]. Electric Power Automation Equipment, 2017, 37(6): 48-54.

[20]李廷钧, 杜欣慧, 姚宏民. 计及用户评价的智能用电社区分层优化调度[J]. 电网技术, 2018, 42(11): 3486-3497.

LI Tingjun, DU Xinhui, YAO Hongmin. Hierarchical optimal dispatching of smart power community considering user evaluation[J]. Power System Technology, 2018, 42(11): 3486-3497.

[21]陆青, 郁浩, 冷亚军, 等. 家庭智能用电任务调度优化模型及其算法研究[J]. 中国电机工程学报, 2018, 38(13): 3826-3836, 4023.

LU Qing, YU Hao, LENG Yajun, et al. Research on optimization model and algorithm of home smart power-consumption task scheduling[J]. Proceedings of the CSEE, 2018, 38(13): 3826-3836, 4023.

[22] RUDOLPH G. Convergence analysis of canonical genetic algorithms[J]. IEEE Transactions on Neural Networks, 1994, 5(1): 96-101.

[23] 季艳芳, 曹炬. 云搜索算法的收敛性分析[J]. 计算机工程与科学, 2011, 33(12): 84-86.

JI Yanfang, CAO Ju. Convergence analysis of cloud search algorithm[J]. Computer Engineering and Science, 2011, 33(12): 84-86.

[24]贺毅朝, 王熙照, 李文斌, 等. 基于遗传算法求解折扣{0-1}背包问题的研究[J]. 计算机学报, 2016, 39(12): 2614-2630.

HE Yichao, WANG Xizhao, LI Wenbin, et al. Research on solving discount {0-1} knapsack problem based on genetic algorithm[J]. Chinese Journal of Computers, 2016, 39(12): 2614-2630.

[25]李耀华, 孔力. 发展太阳能和风能发电技术、加速推进我国能源转型[J]. 中国科学院院刊, 2019, 34(4): 426-433.

LI Yaohua, KONG Li. Develop solar and wind power generation technologies to accelerate energy transition[J]. Journal of the Chinese Academy of Sciences, 2019, 34(4): 426-433.

Optimization of the demand side dispatching of a power grid based on an efficient genetic algorithm and its convergence analysis

PENG Qian, WANG Aijuan, LI Junyang, LIU Wanping

(School of Computer Science and Engineering, Chongqing University of Technology, Chongqing 400054, China)

There has been a great increase in the number of high-power electrical appliances on the smart grid. Together with the popularization of smart terminals, and the increasing power consumption from the demand-side, this has brought the difficulties of power consumption to consumers. In this paper, the demand side scheduling scenario is considered from the three aspects of distributed generation, utility power and residential power consumption. Their time-sharing price models are constructed. Then, we introduce three functions to measure dispatching performance: resident comfort, electricity consumption economy and load variance. We also construct a weighted optimization objective model based on the dispatching performance function. Given that a complex multi-party time-sharing electricity price model participates in the dispatching, we propose an improved genetic algorithm to dispatch electricity consumption of demand side to minimize the objective function. Here additional elite selection strategies and evolutionary reversal operations are added. This can effectively reduce the iteration time and find an optimal value. Then, the convergence of the proposed algorithm is proved theoretically. Finally, the effectiveness of the algorithm is verified by simulation, and the power consumption cost is reduced by 31.29% while meeting the comfort of the resident power consumption.

This work is supported by the National Natural Science Foundation of China (No. 62103070).

genetic algorithm; smart grid; time-sharing electricity price model; demand-side dispatch

10.19783/j.cnki.pspc.210671

国家自然科学基金项目资助(62103070)；重庆市教育科学技术研究项目资助(KJQN202001120)；重庆理工大学研究生创新项目资助(clgycx20203111)

2021-06-05；

2021-11-10

彭 茜(1996—)，女，硕士研究生，研究方向为智能电网；E-mail: 2772536786@qq.com

王爱娟(1989—)，女，通信作者，博士研究生，副教授，研究方向为复杂网络、一致性控制、分布式优化算法、网络安全、经济调度及能源管理。E-mail:aijuan321@foxmail.com

(编辑 姜新丽)