交流配电系统中微网群管控一体化策略

吕智林，宋 健

交流配电系统中微网群管控一体化策略

吕智林，宋 健

(广西大学电气工程学院，广西 南宁 530004)

微网群位于多节点配电网系统中，目前的研究大多只针对微网群的控制策略或能量调度问题，没有同时针对这两种问题进行的研究。因此，提出一种上层调度与下层控制联合优化的管控一体化策略。上层调度系统采用基于二阶锥优化的最优潮流算法对多节点系统进行能量调度，并与节点内微网群实时信息交互。下层微网群控制系统中提出一种改进的混合优化控制策略，在消除无功功率分配不均问题的同时提高系统的有功功率动态性能，并保证电压与频率的一致性稳定收敛。当负荷突变后超过微网群最大发电功率时，以微网群的功率需求作为上下层联动的标准，调用上层根据新的功率需求进行潮流的重新分配，通过通信网络向下层传递更新的参考信号，进行一种调度与控制的有机联动，保证系统的稳定性。仿真采用微网群系统接入30节点配电网运行作为算例，验证了管控一体化策略对系统的稳定性、可靠性和抗干扰性有很大的提高。

微网群；多节点系统；管控一体化；最优潮流；混合优化控制策略

0 引言

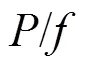
目前大部分的研究中，研究者一般只针对微网群的能量调度或是稳定控制[23-26]，然而调度与控制的有机结合对一个多节点的含微网群的系统是必要的。对此，本文提出了一种调度与控制相结合的管控一体化策略，做到在含微网群的多节点系统中，上层调度和下层控制间的联动。上层采用基于二阶锥优化的最优潮流算法，以网损最小作为目标，进行功率的最优分配。下层微网群内采用一种改进的混合优化下垂控制，通过自适应虚拟阻抗解决无功功率均分问题；利用washout滤波器提升系统的有功功率动态性能；引入一种电压频率二次调整策略，提高系统电压和频率的稳定性。上下层利用功率变化作为参考，通过通信链路交互信息，从而达到调度和控制的管控一体化。上层调度策略按照一定的时段进行多节点系统的功率最优分配；当下层突变量超过功率阈值时，将采取上下层调度与控制的联动策略，保障微网群系统的稳定运行，从而达到调度和控制的管控一体化。最后通过对含微网群的多节点电网络拓扑建立模型并进行仿真算例的试验，验证所提出策略的有效性与可行性。

1 微网群系统管控一体化策略

1.1 含微网群的多节点系统结构

本文构建的微网群系统位于多节点电网络系统中，结构如图1所示。该模型基于IEEE30节点电网络进行拓展。微网群1和微网群2分别通过负载节点7和发电机节点5接入30节点配电网。

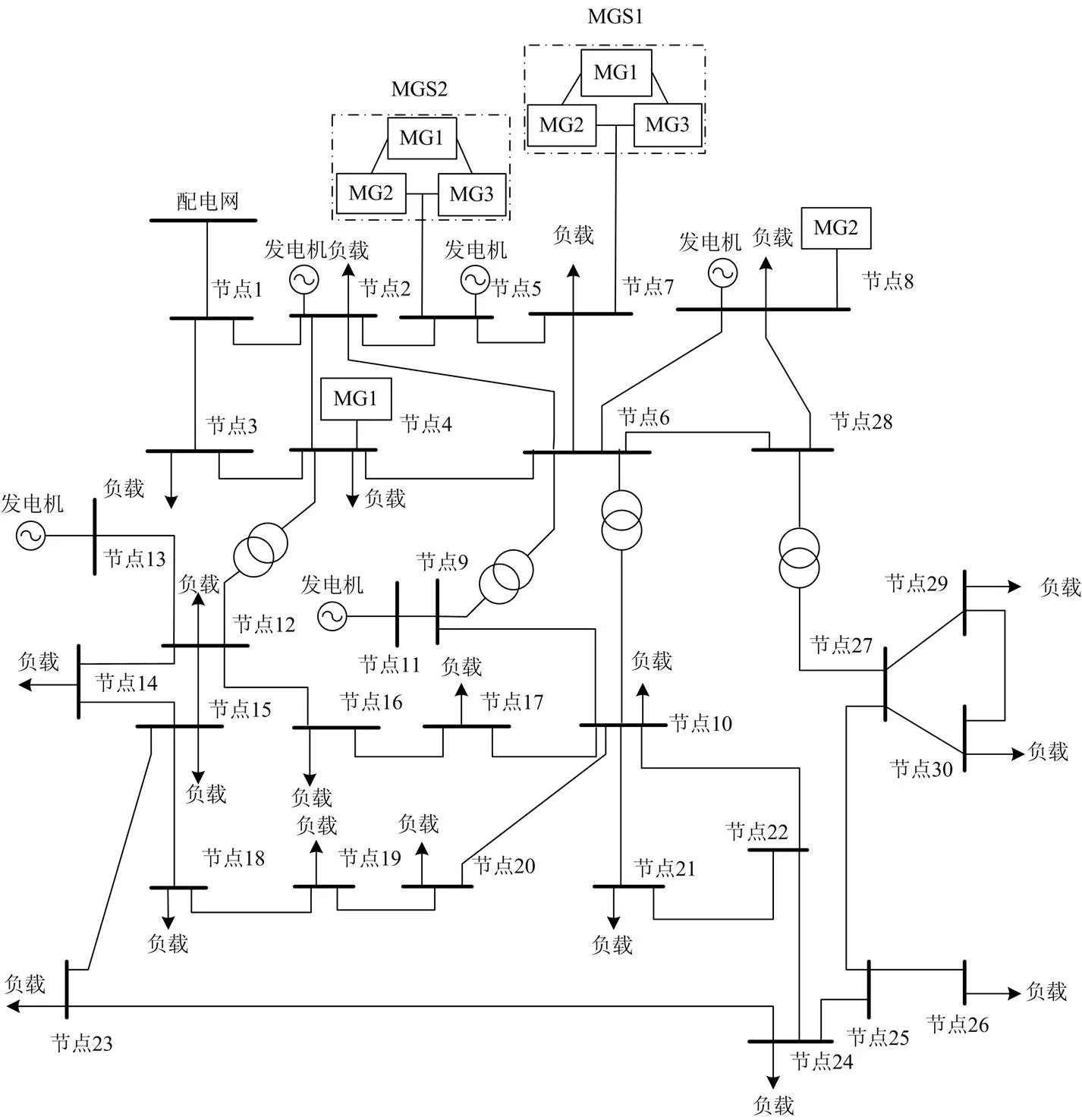
图1 含微网群的30节点模型结构图

1.2 微网群调度与控制策略

系统分为上下两层。其中下层的控制分为三级，第一级主要为微源控制器(Generator Controller, GC)与负荷控制器(Load Controller, LC)，GC主要用于监控微源的实时信息，并生成对应的功率信号，LC主要实时监控微网内与负载相关的信息，负载响应负荷调整指令；第二级主要为子微网控制器(Microgrid Controller, MC)，用于监控微电网实时状态信息，通过网内智能体代理(Microgrid Agent, MA)和上下级进行信息交流，利用改进的混合优化下垂控制协调完成功率分配；第三级为微网群中央控制器(Microgrid Cluster Center Controller, MGCCC)，用于观测微网群内各MC的实时状态。MGCCC收集和处理MC传递而来的信息，通过微网群智能体代理(Microgrid Cluster Agent, MCA)和全局中央控制器(Globel Center Controller, GCC)进行信息交互，接收上层功率调度信号，进行调度和控制。上层调度层为GCC，即是监控器，也是调度器，和MGCCC进行信息交互，实时监控下层的实时状态，并且具有指令调度功能，采用基于二阶锥优化的最优调度优化算法，当下层出现不可平抑的功率、频率波动时，采用该算法对各节点潮流进行重新调度，生成新的参考信号发送到指定的微网群。并且GCC会接收各节点的发电机出力，节点负载变化等信息。在下层没有出现故障时，每隔一定时间，以最小网损作为目标，通过基于二阶锥优化的最优调度优化算法对潮流进行重新规划。调度与控制策略流程图如图2所示。

1.3 微网群调度策略

1.3.1功率阈值与调度策略

设功率阈值为一个微网群理论上的最大可再生能力。设第个微网群的有功功率阈值可以定义为

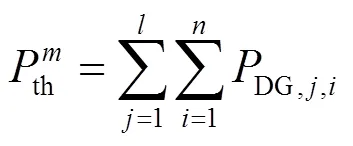
同理，无功功率功率阈值定义如式(2)。

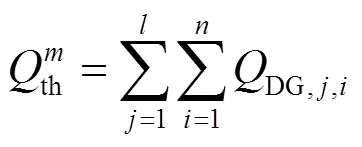
理论最大功率富余可以表示为

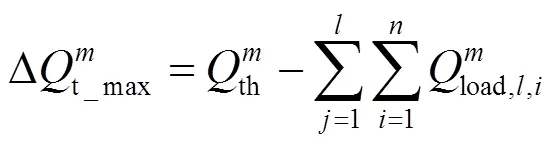
同理，实际功率富余可以表示为

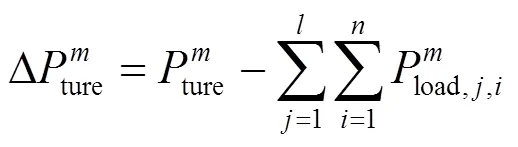
如果实际功率富余为正，则说明微网群输出能量富余，可以向大电网售电或储存；如果实际功率富余为负，则说明微网群处于能量缺乏状态，需要进行切负荷操作或者向大电网寻求能量补给。以各微网群的实际功率富余情况，可以将各个微网群等效为虚拟电源或虚拟负荷。

位于负载节点的微网群正常情况下处于自治状态。处于发电机节点的微网群在无异常状态时，以理论最大功率阈值运行，向大电网输电，作为发电机节点本地电源的能量补偿输出。

1.3.2二阶锥优化的最优潮流功率分配

以多节点网络下的最小网损为目标，建立模型并求最优解。对应的目标函数为

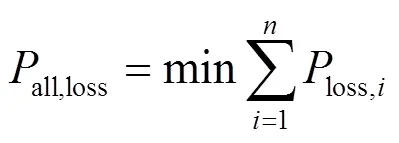
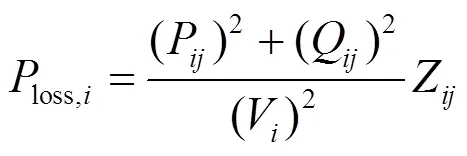
式(9)为功率平衡条件的约束公式。

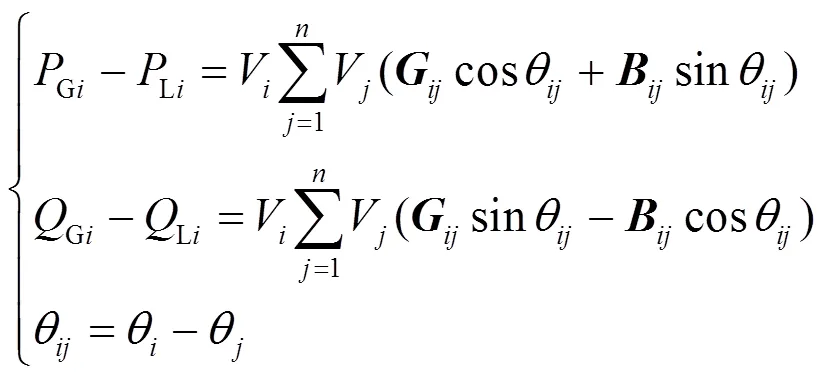
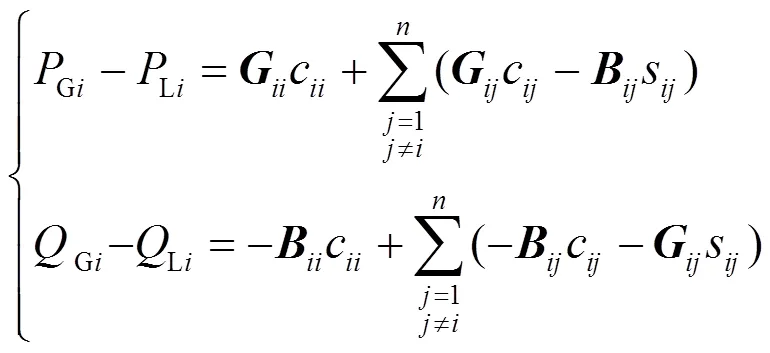
其余的约束条件可以表示为式(11)的形式。

1.4 微网群控制策略

图3为微网群内子微网中分布式电源的基本控制回路，本文基本控制策略采用下垂控制[27-31]，其中washout滤波器控制回路的目的是对/下垂控制进行优化，提高系统的有功动态性能。自适应虚拟阻抗回路的目的是对/下垂控制进行优化，从而提高对无功功率分配的精度。针对微网群运行中的电压不匹配问题，使用一致性电压频率二次调整策略进行优化。

图3 子微网中DGi控制回路模型

1.4.1基于washout滤波器优化的/下垂控制

washout滤波器是一种无低频分量的带通滤波器(BPF)，可以有效地提高微网在功率输出上的动态性能[32-33]，washout滤波器的控制机制可以表示为

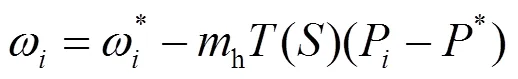
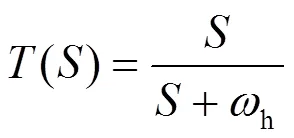
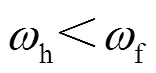
基于冲洗滤波器控制补偿优化的/下垂控制回路的控制方案可以导出为式(16)。

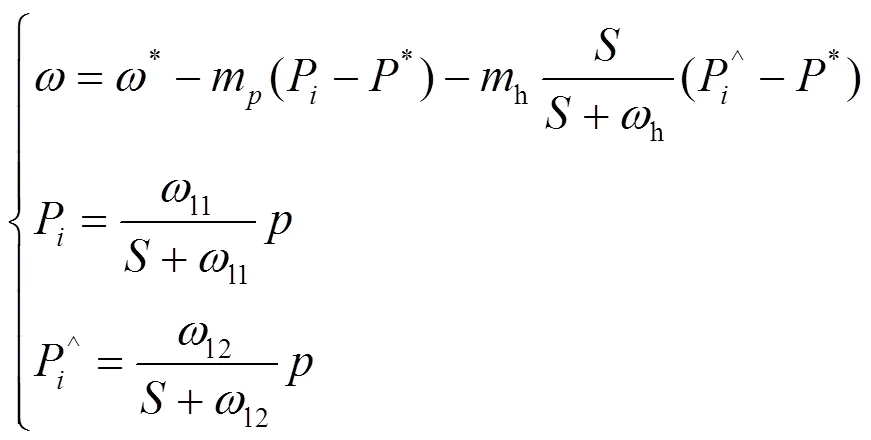
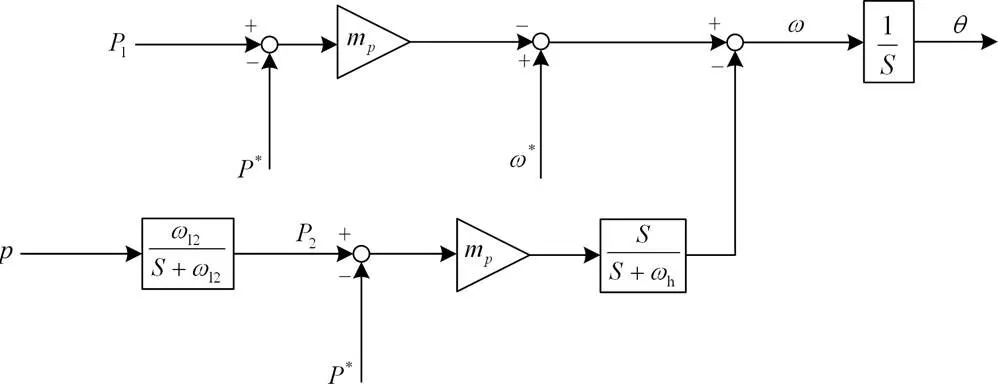
图4 washout滤波器补偿优化的P/f下垂控制器控制框图

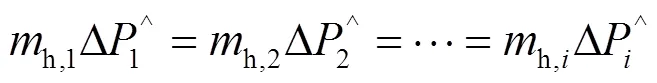
1.4.2一致性自适应虚拟阻抗控制

washout滤波器控制优化的/下垂控制无法对电压进行调节，而电压的幅值差是无功功率分配的必要条件。本文采用基于一致性原理的自适应虚拟阻抗控制来实现无功功率按比例分配。

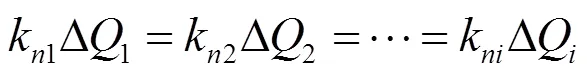
根据式(18)，将其线性化处理可得

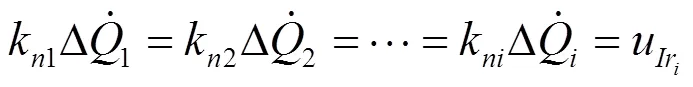
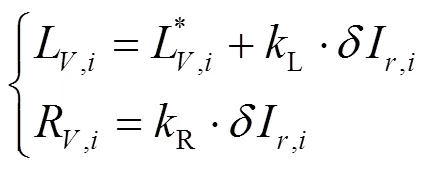
1.4.3基于离散一致性的电压频率二次调整策略

下垂控制会导致电压幅值不一致的问题，并且频率收敛速度较慢。本文提出一种基于离散一致性的下垂控制二次调整策略，通过检测到的电压、频率值进行迭代计算。微网的状态量设定为参考值，使得其可以达到一致性跟踪效果。根据一致性算法，该补偿方法的动态模型为

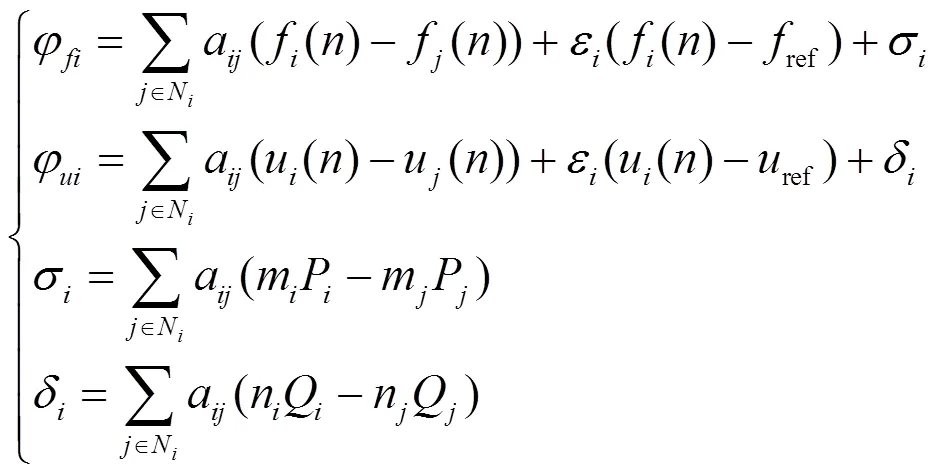
式(25)为该算法的迭代规则。

2 仿真算例分析

2.1 仿真模型

本文通过搭建Matlab/Simulink仿真模型，并运用gurobi优化求解器进行实验。试验所用模型为IEEE30节点模型的拓展模型，微网群1位于节点7，由3个子微网组成，次要负载通过断路器和微网群连接，微网群通过PCC点和大电网连接。

2.2 仿真结果分析

2.2.1含微网群的30节点系统调度策略仿真分析

对实验的30节点系统进行24 h调度计算，该系统的24 h的负载需求变化如图5所示。

图5 含微网群的30节点系统24 h负载需求变化

图5中：08：00—09：00节点7的微网群1投入大负载1.035 MW；15：00—16：00节点5的微网群2投入0.335 MW大负载。因为超出微网群1和微网群2功率阈值，微网群需要大电网进行功率补给。以微网群的功率需求作为等效负荷，上层调度策略对潮流进行重新分配。

基于二阶锥优化算法以网损为目标进行最优潮流计算，得到系统一个调度周期内的网络损耗，如图6所示。

图6 含微网群的30节点系统24 h网络损耗

因为潮流进行了重新规划，所以在图6，系统的网损和发电成本也发生了相应的变化，其中08：00—09：00网损由1.56 MW变为1.57 MW；15：00—16：00网损由1.27 MW变为1.28 MW。

2.2.2负载节点7下微网群1仿真算例分析

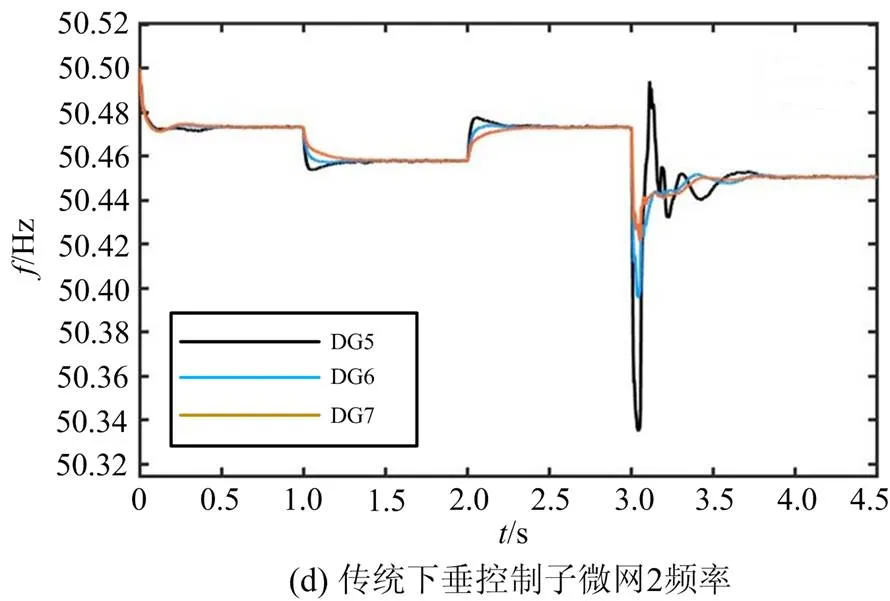
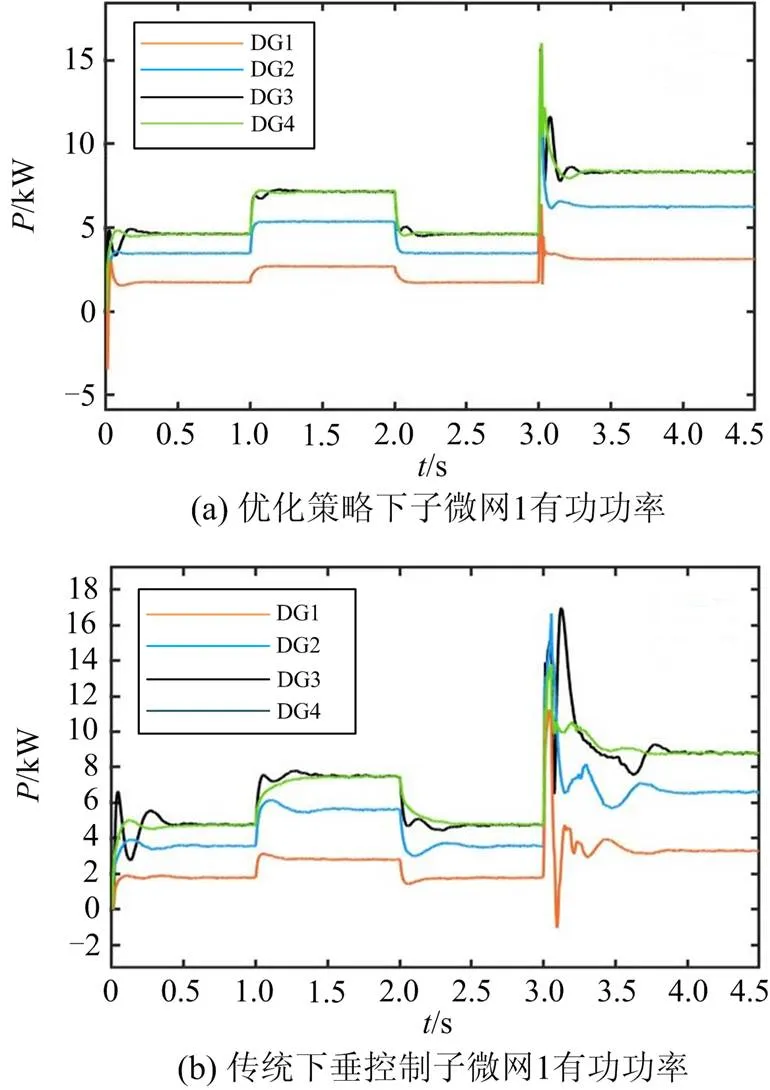
图7—图10是以微网群1为例，在使用调度与控制一体化策略后，对改进的混合优化下垂控制和传统下垂控制进行对比的仿真结果。

在0～1 s时，系统各自带本地负荷以及公共负载运行。在1～2 s时，出现负载投入的状况，负载容量为20 kW，未达到微网群的功率阈值，电网络依旧按照初始潮流运行。

通过图10可以看出，1～2 s内传统下垂控制策略无功功率无法达到均分，而文中所采用的控制策略使各子微网无功仍按4:4:3:1.5，4:3:1.5，3:3:1.5等比例均匀分配。

在2 s后，负载切出，通过图例对比，使用控制策略优化后的微网群显然拥有更快的恢复速度且恢复过程更稳定平滑，2～3 s时微网群恢复到正常运行。在第3 s出现负载投入，所投入负载为1.035 MW，功率需求大于微网群1的功率阈值参考值。此时，MGCCC接收到LC传递的功率波动信息进行切负荷操作。切除次要负荷后，功率需求量依旧高于功率阈值，通过下层的控制无法完成电压、频率波动的平抑和功率的分配。

此时，节点7下的微网群1需要功率补给。GCC进行优化计算，通过上层调度策略采用二阶锥优化算法对30节点拓扑的功率潮流进行最优重新分配。表1为日前计划调度下各发电机节点出力。表2为各节点在重新分配潮流后各发电机节点出力。表2有功出力总和与表1的差值为1.01 MW，其中从配电网处得到的功率补给为1 MW，0.01 MW为重新规划出力后网损的变化值。

微网群1在得到功率补给后，以功率阈值参考值运行。通过图9和图10的对比可知，采用了优化控制策略后，相较于传统下垂控制，有功功率收敛速度更快且波动更小，具有更好的动态性能，无功功率可以按比例合理分配。通过图7可以看出，与传统下垂控制相比，采用优化策略后频率波动相对减少，且收敛时间大幅减少，提高了系统的稳定性。通过图8可以看出，在实验的整个过程中，采取优化策略后的各分布式电源的电压均趋于一致性收敛且变化过程平滑稳定，而传统下垂控制下的各分布式电源的电压无法达到一致性收敛，电能质量和稳定性远低于采用优化策略。

表1 08：00—09：00日前计划调度各发电机组出力

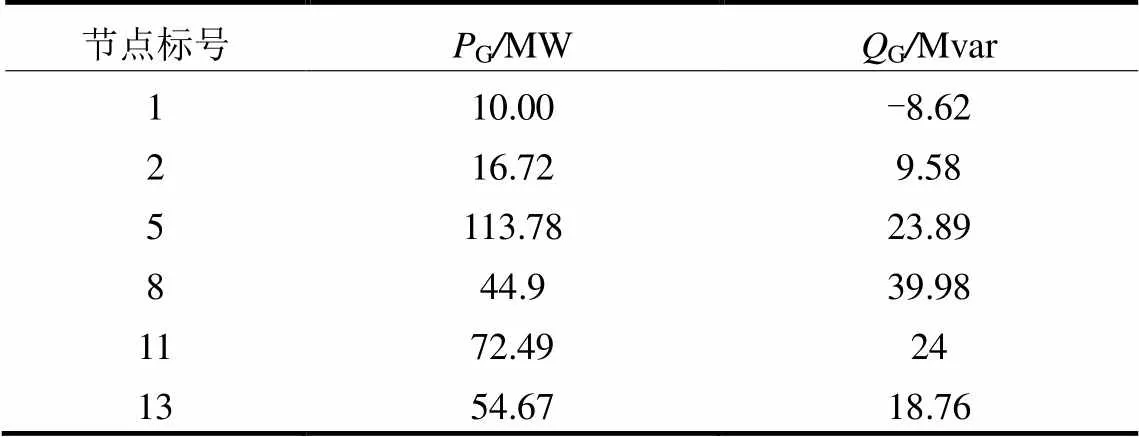
表2 08：00—09：00潮流重新规划后各发电机组出力

2.2.3电源节点5下微网群2仿真算例分析

微网群2按照最大功率阈值发电，在能满足向微网群内部负载供电的情况下，以实际最大功率富余向大电网售电。在15：00—16：00由于投入过大负载，根据调度和控制策略，微网群2停止向大电网售电，向大电网购电。

图11—图14是以位于发电机节点的微网群2中子微网1为例进行分析，在使用调度与控制策略后，和传统下垂控制进行对比的仿真结果。

在0～1 s时，系统以最大功率阈值输出功率。在1～2 s时，节点5下微网群2中出现负载突变的状况，投入负载容量为20 kW，通过计算理论最大功率富余参考值可知，接入20 kW负载未达到微网群的功率阈值，仅采用控制策略进行控制。

负载切出后，在2～3 s时，微网群恢复到以理论最大功率富余运行的状态。在第3 s时，0.335 MW大负载投入。此时功率需求大于微网群2的功率阈值参考值。微网群首先停止向配电网售电，在切除次要负荷5 kW后，功率需求量依旧高于功率阈值。此时，通过上层调度策略进行功率的重新调度，表3为日前计划调度下各发电机节点发电机组出力。潮流重新分配后，新的功率调度如表4。其中表4的有功出力总和与表3的差值为0.31 MW，其中微网群2的功率需求补给为0.3 MW，0.01 MW为重新规划出力后网损的变化值。

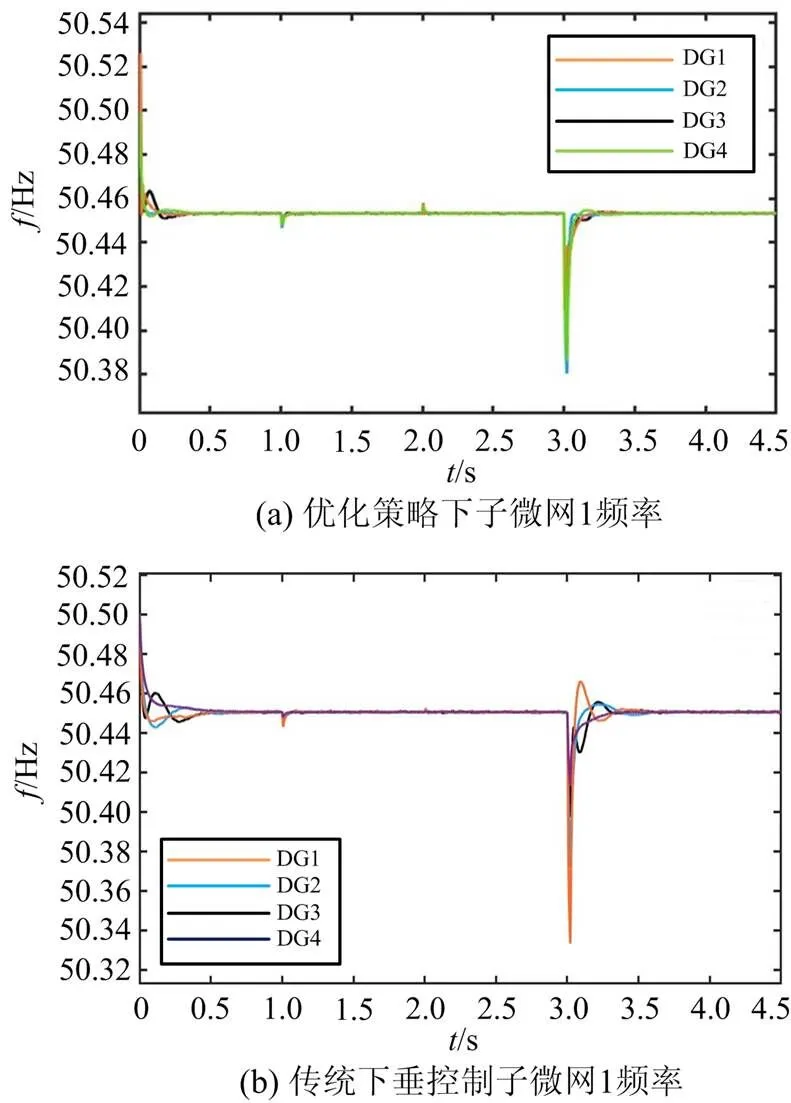
图11 微网群2中子微网1频率变化对比图

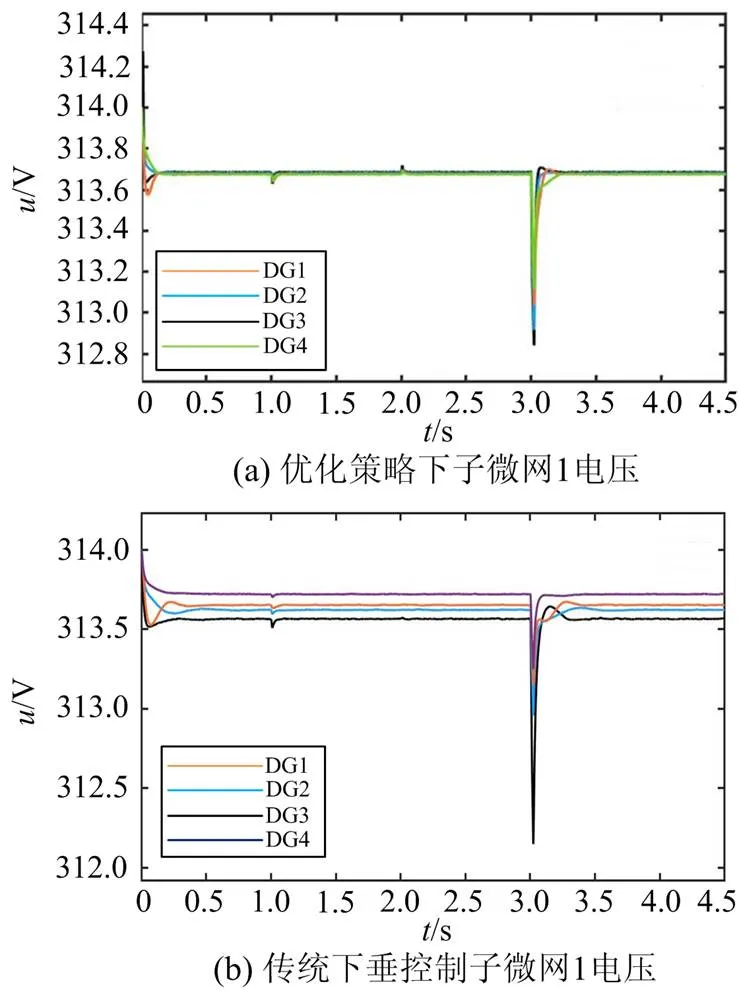
图12 微网群2中子微网1电压变化对比图

图13 微网群2中子微网1有功功率变化对比图

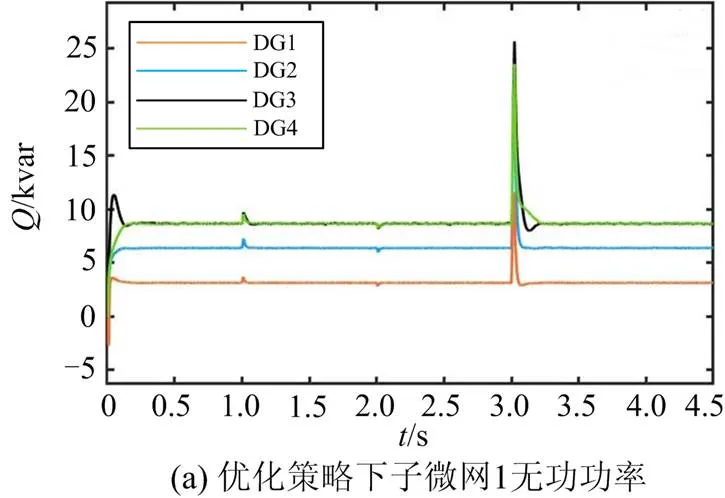
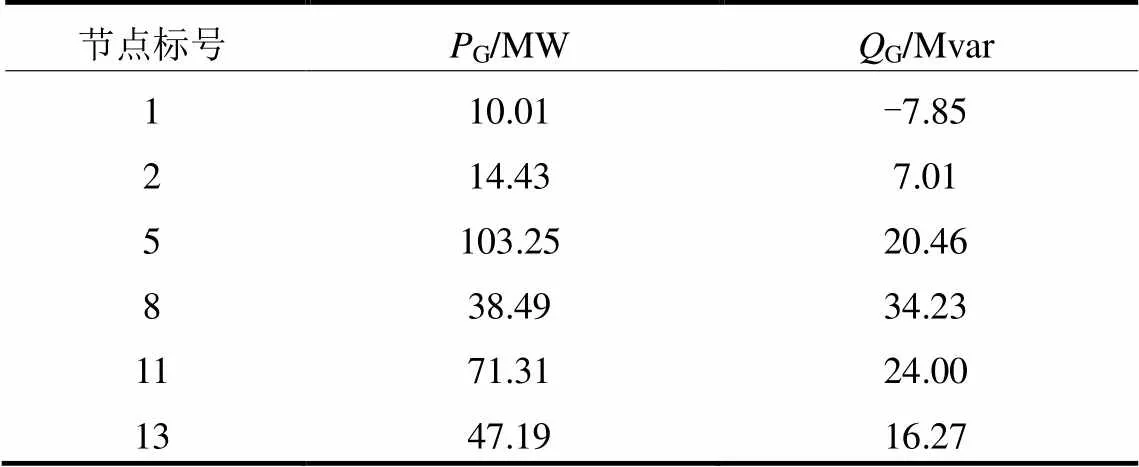
表3 15：00—16：00日前计划调度各发电机组出力

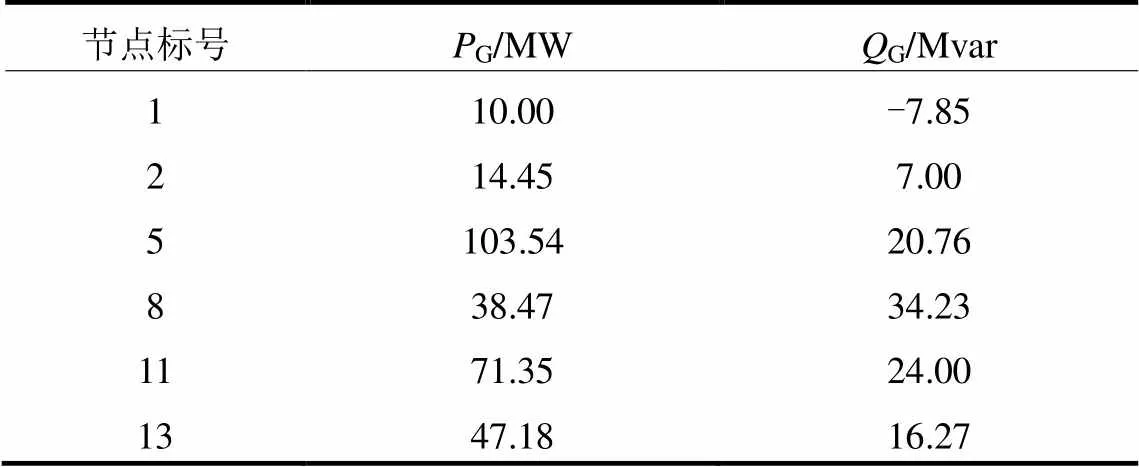
表4 15：00—16：00潮流重新规划后各发电机组出力

通过图11—图14中子微网1中采用优化策略与传统下垂控制作对比，加入优化控制策略后子微网1电压趋于一致性收敛，且电压和频率更加稳定，传统下垂控制则无法做到电压一致性，且电压和频率的性能较差；优化后的有功功率动态性能优于传统下垂控制；传统下垂控制无法做到无功功率的等比例均分，采用优化后则解决了这一问题，提高了微网群系统的功率分配性能和稳定性。

2.2.4调度与控制一体化策略必要性仿真分析

如果不进行调度与控制的一体化，仅使用控制策略的话，在一些情况下则会对电力系统和微网群的安全造成极大的威胁。图15为不含上层最优潮流调度仅采用下层控制的微网群1下以子微网1为例的实验结果，在第3 s超大负载接入后，其频率、电压和功率发生巨大的不可平抑波动，对电力系统和微网群将造成极大的冲击。其频率变化范围最大时超过了0.2 Hz，在一些对频率变化要求高的场合会造成很大的危害。

图15 不采用上层调度策略的微网群1中子微网1频率、电压及功率变化

3 结论

针对目前微网群研究中一般只针对能量调度或控制策略、研究缺乏全局性这一问题，提出一种调度与控制策略相结合的管控一体化方案，系统分为可互相联动的上下两层，从而达到能量调度策略与控制策略的协调。

1) 上层为调度层，微网群系统通过PCC点接入多节点大电网。上层以各节点的当前出力值预测和当前负载为输入，大电网的网损最小为目标，进行最优潮流计算。

2) 下层为微网群控制层，引入一致控制策略，构造自适应虚拟阻抗来实现了无功功率成比例分配；引入washout滤波器，显著提升系统有功动态性能，减少有功调节时间；引入电压频率二次调整策略，使得微网群中各分布式电源的电压趋于一致性收敛且电压和频率的变化更加稳定平滑，解决了传统下垂控制电压不能趋于一致且频率性能较差的问题。

3) 通过上下层联动可以使得微网群系统在多节点大电网系统中处于安全稳定的运行状态，上层调度策略在正常情况下按照一定的时段进行潮流最优分配；当下层出现负载突变，优先使用控制策略进行合理控制，当下层控制策略无法平抑突变时，将会启用上层调度策略进行潮流的重新分配，对故障微网群或微网进行能量补给，下层控制策略迅速调整各自的出力，很快再次收敛，重新达到新的平衡状态。

上述调度与控制一体化策略能使含微网群的多节点配电网系统形成一个高效、稳定与抗干扰能力极强的系统，在经济性、可靠性与鲁棒性上得到很大提高。

本文针对交流配电系统下，对交流微网群的管控一体化策略进行了研究，然而对于交直流混合微网群在该策略下的控制方法应如何改进，还需对其进一步深入探讨。

[1] 支娜, 肖曦, 田培根, 等. 微网群控制技术研究现状与展望[J]. 电力自动化设备, 2016, 36(4): 107-115.

ZHI Na, XIAO Xi, TIAN Peigen, et al. The research status and prospect of micro network group control technology[J]. Electric Power Automation Equipment, 2016, 36(4): 107-115.

[2] 陈磊, 牛玉刚, 贾廷纲. 基于主从博弈的多微网能量调度策略[J]. 电力系统保护与控制, 2020, 48(19): 35-42.

CHEN Lei, NIU Yugang, JIA Tinggang. Multi microgrid energy dispatch strategy based on master-slave game[J]. Power System Protection and Control, 2020, 48(19): 35-42.

[3] 于国星, 宋蕙慧, 侯睿, 等. 柔性直流互联孤岛微网群的分布式频率协同控制[J]. 电力系统自动化, 2020, 44(20): 103-111.

YU Guoxing, SONG Huihui, HOU Rui, et al. Distributed cooperative frequency control for flexible DC interconnected island microgrid cluster[J]. Automation of Electric Power Systems, 2020, 44(20): 103-111.

[4] 葛少云, 李吉峰, 刘洪, 等. 考虑智能建筑特性的多微网端对端能量交易方法[J]. 电力系统自动化, 2021, 45(6): 203-214.

GE Shaoyun, LI Jifeng, LIU Hong, et al. Peer-to-peer energy trading method for multiple microgrids considering characteristics of smart building[J]. Automation of Electric Power Systems, 2021, 45(6): 203-214.

[5] AMOATENG D O, ALHOSANI M, ELMOURSI M S, et al. Adaptive voltage and frequency control of islanded multi-microgrids[J]. IEEE Transactions on Power Systems, 2018, 33(4): 4454-4465.

[6] LIU Y, LI Y, XIN H, et al. Distributed optimal tie-line power flow control for multiple interconnected AC microgrids[J]. IEEE Transactions on Power Systems, 2019, 34(3): 1869-1880.

[7] 李霞林, 李志旺, 郭力, 等. 交直流微电网集群柔性控制及稳定性分析[J]. 中国电机工程学报, 2019, 39(20): 5948-5961, 6175.

LI Xialin, LI Zhiwang, GUO Li, et al. Flexible control and stability analysis of AC / DC microgrid cluster[J]. Proceedings of the CSEE, 2019, 39(20): 5948-5961, 6175.

[8] 黄文焘, 吴攀, 邰能灵, 等. 基于混合公共连接单元的柔性互联多微网结构与控制方法[J]. 中国电机工程学报, 2019, 39(12): 3499-3514.

HUANG Wentao, WU Pan, TAI Nengling, et al. Structure and control method of flexible interconnected multi microgrid based on hybrid common connection unit[J]. Proceedings of the CSEE, 2019, 39(12): 3499-3514.

[9] 熊雄, 吴鸣, 季宇, 等. 微网群混合协调控制及功率管理策略研究[J]. 中国电机工程学报, 2018, 38(5): 1419-1427.

XIONG Xiong, WU Ming, JI Yu, et al. Research on hybrid coordinated control and power management strategy of microgrid Group[J]. Proceedings of the CSEE, 2018, 38(5): 1419-1427.

[10] 马覃峰, 邵震霞, 康鹏, 等. 多端柔性直流电网公共直流电压协同控制方法[J]. 南方电网技术, 2017, 11(5): 24-28, 62.

MA Qinfeng, SHAO Zhenxia, KANG Peng, et al. Public DC voltage collaborative control method for multi terminal flexible DC power grid[J]. Southern Power System Technology, 2017, 11(5): 24-28, 62.

[11] 邓诗蕾, 王明渝. 直流微电网潮流控制器与分布式储能协同控制策略[J]. 电力系统保护与控制, 2018, 46(24): 40-46.

DENG Shilei, WANG Mingyu. Coordinated control strategy of DC microgrid power flow controller and distributed energy storage[J]. Power System Protection and Control, 2018, 46(24): 40-46.

[12] LU X, LAI J, YU X. A novel secondary power management strategy for multiple AC microgrids with cluster-oriented two-layer cooperative framework[J]. IEEE Transactions on Industrial Informatics, 2021, 17(2): 1483-1495.

[13] LU Xiaoqing, LAI Jingang, YU Xinghuo. Distributed coordination of islanded microgrid clusters using a two-layer intermittent communication network[J]. IEEE Transactions on Industrial Informatics, 2018, 14(9): 3956-3969.

[14] 乐健, 周谦, 王曹, 等. 无功补偿设备和分布式电源协同的配电网优化控制策略研究[J]. 电力系统保护与控制, 2020, 48(18): 38-47.

LE Jian, ZHOU Qian, WANG Cao, et al. Research on optimal control strategy of distribution network coordinated by reactive power compensation equipment and distributed generation[J]. Power System Protection and Control, 2020, 48(18): 38-47.

[15] AREFI A, SHAHNIA F. Tertiary controller-based optimal voltage and frequency management technique for multi-microgrid systems of large remote towns[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 5962-5974.

[16] LI Y, ZHAO T, PING W, et al. Optimal operation of multi-microgrids via cooperative energy and reserve scheduling[J]. IEEE Transactions on Industrial Informatics, 2018, 14(8): 3459-3468.

[17] XIAO L, MANDAYAM N B, POOR H V. Prospect theoretic analysis of energy exchange among microgrids[J]. IEEE Transactions on Smart Grid, 2015, 6(1): 63-72.

[18] ESSAYEH C, ELFENNI M R, DAHMOUNI H. Optimization of energy exchange in microgrid networks: a coalition formation approach[J]. Protection and Control of Modern Power Systems, 2019, 4(1): 24-33.

[19] ESMAEILI S, ANVARI-MOGHADDAM A, JADID S. Optimal operational scheduling of re-configurable multi-microgrids considering energy storage systems[J]. Energies, 2019, 12(9): 1766-1786.

[20] WANG H, HUANG J. Incentivizing energy trading for inter-connected microgrids[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 2647-2657.

[21] LÜ T, AI Q, ZHAO Y. A bi-level multi-objective optimal operation of grid-connected microgrids[J]. Electric Power Systems Research, 2016, 131(2): 60-70.

[22] 孙强, 谢典, 聂青云, 等. 含电-热-冷-气负荷的园区综合能源系统经济优化调度研究[J]. 中国电力, 2020, 53(4): 79-88.

SUN Qiang, IE Dian, NIE Qingyun, et al. Research on economic optimization scheduling of park integrated energy system with electricity-heat-cool-gas load[J]. Electric Power, 2020, 53(4): 79-88.

[23] 武梦景, 万灿, 宋永华, 等. 含多能微网群的区域电热综合能源系统分层自治优化调度[J]. 电力系统自动化, 2021, 45(12): 20-29.

WU Mengjing, WAN Can, SONG Yonghua, et al. Hierarchical autonomous optimal dispatching of district integrated heating and power system with multi-energy microgrids[J]. Automation of Electric Power Systems, 2021, 45(12): 20-29.

[24] 苏磊, 李振坤, 张智泉, 等. 基于机会约束规划的综合能源微网群协调运行策略研究[J]. 电力系统保护与控制, 2021, 49(14): 123-131.

SU Lei, LI Zhenkun, ZHANG Zhiquan, et al. A coordinated operation strategy for integrated energy microgrid clusters based on chance-constrained programming[J]. Power System Protection and Control, 2021, 49(14): 123-131.

[25] 练小林, 李晓露, 陆一鸣, 等. 可交易能源框架下的微网群动态电能交易策略[J]. 电力建设, 2020, 41(6): 18-27.

LIAN Xiaolin, LI Xiaolu, LU Yiming, et al. Dynamic electricity trading strategy for multi-microgrid under transactive energy framework[J]. Electric Power Construction, 2020, 41(6): 18-27.

[26] 阮绵晖, 郑建平, 刘尧, 等. 离网直流微网群混合储能容量优化配置方法[J]. 电力工程技术, 2021, 40(3): 99-105.

RUAN Mianhui, ZHENG Jianping, LIU Yao, et al. Optimization configuration method for hybrid energy storage capacity of independent DC microgrid cluster[J]. Electric Power Engineering Technology, 2021, 40(3): 99-105.

[27]王二永, 王帅. 基于自适应虚拟电阻的低压微电网下垂控制策略[J]. 电力系统保护与控制, 2020, 48(2): 144-149.

WANG Eryong, WANG Shuai. Droop control strategy of low voltage microgrid based on adaptive virtual resistance[J]. Power System Protection and Control, 2020, 48(2): 144-149.

[28] LAI J, LU X, YU X, et al. Cluster-oriented distributed cooperative control for multiple AC microgrids[J]. IEEE Transactions on Industrial Informatics, 2019, 15(11): 5906-5918.

[29] SUN Y, SHI G, LI X, et al. An f-P/Q droop control in cascaded-type microgrid[J]. IEEE Transactions on Power Systems, 2018, 33(1): 1136-1138.

[30]徐经民, 徐在德, 童超. 基于模糊下垂控制的VSC-HVDC交直流系统潮流计算方法[J]. 电力系统保护与控制, 2019, 47(20): 50-57.

XU Jingmin, XU Zaide, TONG Chao. Power flow calculation method of VSC-HVDC AC/DC system based on fuzzy droop control[J]. Power System Protection and Control, 2019, 47(20): 50-57.

[31] 米阳, 王鹏, 邓锦, 等. 孤岛交直流混合微电网群分层协调控制[J]. 电力系统保护与控制, 2021, 49(20): 1-8.

MI Yang, WANG Peng, DENG Jin, et al. Hierarchical coordinated control of island AC/DC hybrid microgrids[J]. Power System Protection and Control, 2021, 49(20): 1-8.

[32] YAZDANIAN M, MEHRIZI-SANI A. Washout filter-based power sharing[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 967-968.

[33] 孙黎霞, 周照宇, 温正赓, 等. SPWM-H桥变换器中分岔与混沌的自适应载波调幅控制[J]. 电测与仪表, 2020, 57(23): 101-108.

SUN Lixia, ZHOU Zhaoyu, WEN Zhenggeng, et al. Adaptive carrier amplitude modulation control of bifurcation and chaos in SPWM H-bridge converter[J]. Electrical Measurement & Instrumentation, 2020, 57(23): 101-108.

Integrated management and control strategy for a microgrid group in an AC distribution system

LÜ Zhilin, SONG Jian

(College of Electrical Engineering, Guangxi University, Nanning 530004, China)

A microgrid cluster is located in a multi node distribution network system. Most current research focuses only either on the control strategy or energy scheduling problem of the microgrid cluster, but not on both problems together. Therefore, an integrated management and control strategy of joint optimization of upper scheduling and lower control is proposed. The upper scheduling system uses an optimal power flow algorithm based on second-order cone optimization to schedule the energy of the multi node system, and interacts with the real-time information of the microgrid group in the node. An improved hybrid optimal control strategy is proposed in the lower microgrid group control system. This can eliminate the uneven distribution of reactive power, improve the dynamic performance of active power, and ensure the consistency and stable convergence of voltage and frequency. When the load exceeds the maximum generating power of the microgrid group after a sudden change, the power demand of the microgrid group is taken as the linkage standard of the upper and lower layers, and the upper layer is called on to reallocate the power flow according to the new power demand, and an updated reference signal is transmitted to the lower layer through the communication network to carry out an organic linkage of regulation and control, so as to ensure the stability of the system. The simulation results show that the integrated management and control strategy can greatly improve the stability, reliability and anti-interference of the system.

This work is supported by the National Natural Science Foundation of China (No. 61364027).

microgrid group; multi node system; integration of management and control; optimal power flow; hybrid optimal control strategy

10.19783/j.cnki.pspc.210670

国家自然科学基金项目资助(61364027)；广西自然科学基金面上项目资助(2019GXNSFAA185011)

2021-06-04；

2021-10-26

吕智林(1971—)，女，通信作者，博士，教授，研究方向为智能电网、复杂系统优化及控制；E-mail: luzhilin2001@ 163.com

宋 健(1997—)，男，硕士研究生，研究方向为微网群调度与控制。E-mail: 13635554987@163.com

(编辑 周金梅)