车辆自动驾驶纵向运动控制优化及求解算法

王 韬，曲大义，徐 胜，贾彦峰，宋 慧

（1.青岛理工大学机械与汽车工程学院，山东 青岛 266520；2.淄博职业学院人工智能与大数据学院，山东 淄博 255300；3.哲晰软件技术（上海）有限公司自动驾驶数据服务部，上海 201815）

为了实现自动和安全驾驶，自动驾驶车辆利用车载传感器感知周围环境，基于当前的交通状况动态规划路径，通过操控车速进行运动控制［1］。自动驾驶应用包括车辆的纵向和侧向运动控制，而大多数纵向和侧向控制问题都可以在模型预测控制（Model Predictive Control，MPC）的 框 架 下 表述［2-3］。本文考虑车辆的纵向运动控制，相应的MPC 问题为约束线性二次MPC 问题。将MPC 应用于车辆纵向运动控制，需要在短时间内处理大量数据，完成高强度计算任务，因此，采用有效的求解算法是实现MPC的关键。

求解该MPC 问题的优化方法有离线和在线方法，其中在线方法更为常见［4-5］。在线方法主要包括有效集方法和内点法两种迭代方法。这两种方法均需求解比较复杂且容易引起数值问题的大规模线性方程组，当进入实时实现时，由于计算复杂使得在实时系统中编码困难［6］。为减小计算负担，可利用由典型的线性二次MPC 问题产生的二次规划（Quadratic Programming，QP）问题的结构来简化数值方法的实现，以及采用更有效的数值方法进行求解［7］。

本文采用拉格朗日松弛法将等式约束引入到目标函数中，并用拉格朗日乘子向量作为对违反约束的惩罚来软化硬约束，通过欧氏投影移除不等式约束以减轻计算负担，采用Nesterov 快速梯度法进行求解［8］，避免了上述方法存在的各种问题，实现了对车辆纵向运动控制快速QP 求解器的开发。

1 车辆纵向运动模型

在MPC 框架下，车辆自动驾驶的纵向位移（位置）、速度和加速度等关键变量的最优值均作为有限时域约束最优控制问题的解得到，因此建立离散形式的车辆纵向运动模型如下：

式中：ts为采样周期；xk、vk、ak和a′k分别为在预测时域内第k点车辆的纵向位移、速度、加速度和加速度的变化率，并且各变量的取值受到其最大和最小值限制。

2 基于约束线性二次MPC 表达式建立QP模型

对于纵向参考跟踪问题，引入状态向量wk=[xk，vk，ak]T，输入向量uk=[a′k]，状态向量参考值wk(ref)=[xk(ref)，vk(ref)，ak(ref)]T，输 入 向 量 参 考 值uk(ref)=[a′k(ref)]，则可得到相应的约束线性二次MPC优化问题为

式中：w、wf和U分别为状态向量wk、wN和输入向量uk的约束集；Q、Qf和R分别为相应的权重矩阵；A、B分别为状态矩阵和输入矩阵。

由式（1）可得

式中：z为新的优化向量，z∈R4N+3；H为新形成的海森矩阵，H∈R(4N+3)×(4N+3)；g∈R4N+3；C为新的约束矩 阵，C∈R3N×(4N+3)；b∈R3N；Z为z的闭凸集，z⊆R4N+3。此处Rn和Rm×n分别表示由n维实向量（n×1 实矩阵）和m×n实矩阵构成的集合。有关矩阵和向量的表达式如下：

式中：I为3阶单位矩阵。

采用新的优化向量z可以使矩阵C为一带状矩阵，从而使后续有关计算更容易。

3 拉格朗日对偶问题及其求解

3.1 对偶问题的转化及快速梯度法求解

对于式（4）的QP问题，应用拉格朗日松弛法可以得到拉格朗日函数如下：

式中：λ为拉格朗日乘子向量，λ∈R3N。

拉格朗日函数的对偶函数为

d(λ)给出了原QP 问题的最优值p*的下界，即有d(λ)≤p*，而且d(λ)是一个无约束凹函数［9-10］，通过求解拉格朗日对偶问题即优化问题可以得到最优拉格朗日乘子λ*，找到原问题最优值的最好下界d*=d(λ*)，而如果原问题与其对偶问题保持强对偶性［11］，则p*=d*，原问题的最优解可由z*(λ)得到，z*(λ)为

最终，可将原QP 问题转化为包含两层优化问题的拉格朗日对偶问题，即

采用Nesterov 快速梯度法求解该对偶问题时，内层QP 问题可通过将准确解投影到箱型边界经一步计算准确地求解，即有

式中：PZ为在凸集上的投影。

将z*(λ)代入拉格朗日函数，可得到拉格朗日对偶函数，进而得到需要求解的拉格朗日对偶问题，再借助对偶函数的梯度即可完成快速梯度法求解，对偶函数的梯度为

本文设计的求解拉格朗日对偶问题的快速梯度法算法如表1 所示。其中，为λ的初始估计值，L为李普希茨常数，Kmax为最大迭代次数。

表1 求解拉格朗日对偶问题的快速梯度法算法Tab.1 Algorithm of fast gradient method for solving the Lagrange dual problem

3.2 最优李普希茨常数的计算

在海森矩阵为正定的条件下，对偶函数d(λ)具有李普希茨连续梯度，即满足

其李普希茨常数为［12］

式中：‖C‖为矩阵C的范数，它等于C的最大奇异值；λmin(H)为H的最小特征值。

引入变量的线性变换z=Py，此处P可逆并选用对角阵，则可得到求解最优李普希茨常数的优化问题为

为求解该优化问题，引入如下结果：

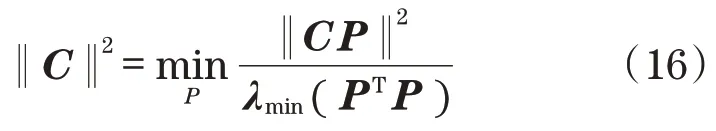
若计算最优李普希茨常数困难，则可用自适应搜索法找到该常数一个合理的值。

3.3 最小迭代下界分析

求解拉格朗日对偶问题的要求为

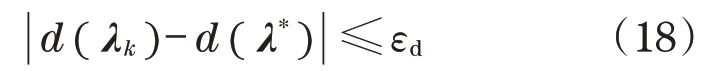
式中：εd为控制误差；最优值d(λ*)事先未知，可用第k次迭代其值的下界代替。

利用快速梯度法收敛速度的上界则有

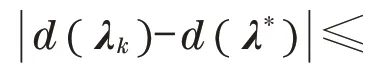
式中：μ、k分别为强凸函数的凸性参数和迭代次数。

在算法采用最优李普希茨常数后，其达到控制误 差εd的 充 分 条 件 是 经 过kεd次 迭 代 后 停止［13］，kεd为

最小迭代下界kεd由L*、和εd决定，而只要优化问题的框架确定了L*和εd就均为常数值，由λ0和Λ*决定，要得到Λ*比较困难，但如果选择了合适的λ0则可以优化kεd。

3.4 停止准则的确定

选用对偶函数梯度的范数‖ ∇d(λ) ‖作为停止准则。从QP 的观点看，如果‖ ∇d(λ) ‖=0 得到完全满足，那么就可以将由λ恢复的最终解z(λ)看作是最优解。从MPC 的角度看，只要‖ ∇d(λ) ‖能收敛于0，那么随着迭代的进行预测结果就将趋近于最优计算值，这意味着与车辆模型运动学匹配得较好。在实际应用中，因计算简单，综合停止准则可用‖ ∇d(λ)‖2，而将其展开后可得

4 计算结果分析

车辆纵向运动控制参数如表2 所示，其中一些参数用于为QP问题构造箱型边界。

表2 车辆纵向运动控制参数Tab.2 Parameters for vehicle longitudinal motion control

为了获得良好的车辆纵向运动控制性能，经过仔细调试得到权重矩阵如下：

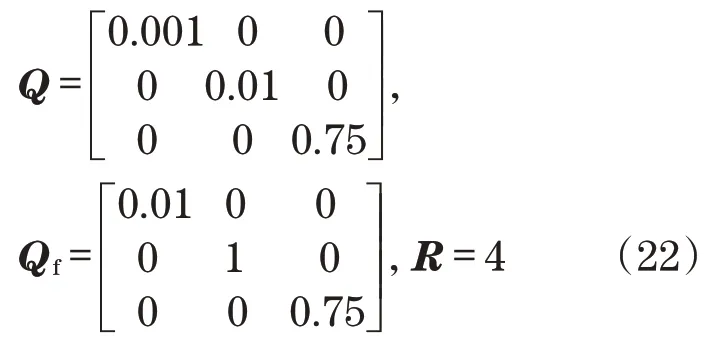
4.1 不同停止准则迭代结果

求解过程中综合停止准则值随迭代次数的变化情况如图1 所示。经过约500 次迭代‖ ∇d(λ)‖2收敛于10-2，而对于位移和速度不需要达到这样小的值。

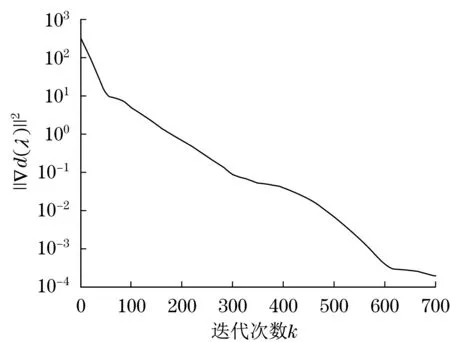
图1 综合停止准则值随迭代次数的变化Fig.1 Relation between the comprehensive stopping criterion values and iterations

求解过程中分解的停止准则值随迭代次数的变化情况如图2 所示。与加速度停止准则相比，位移和速度停止准则可以分别设置较大的控制误差。

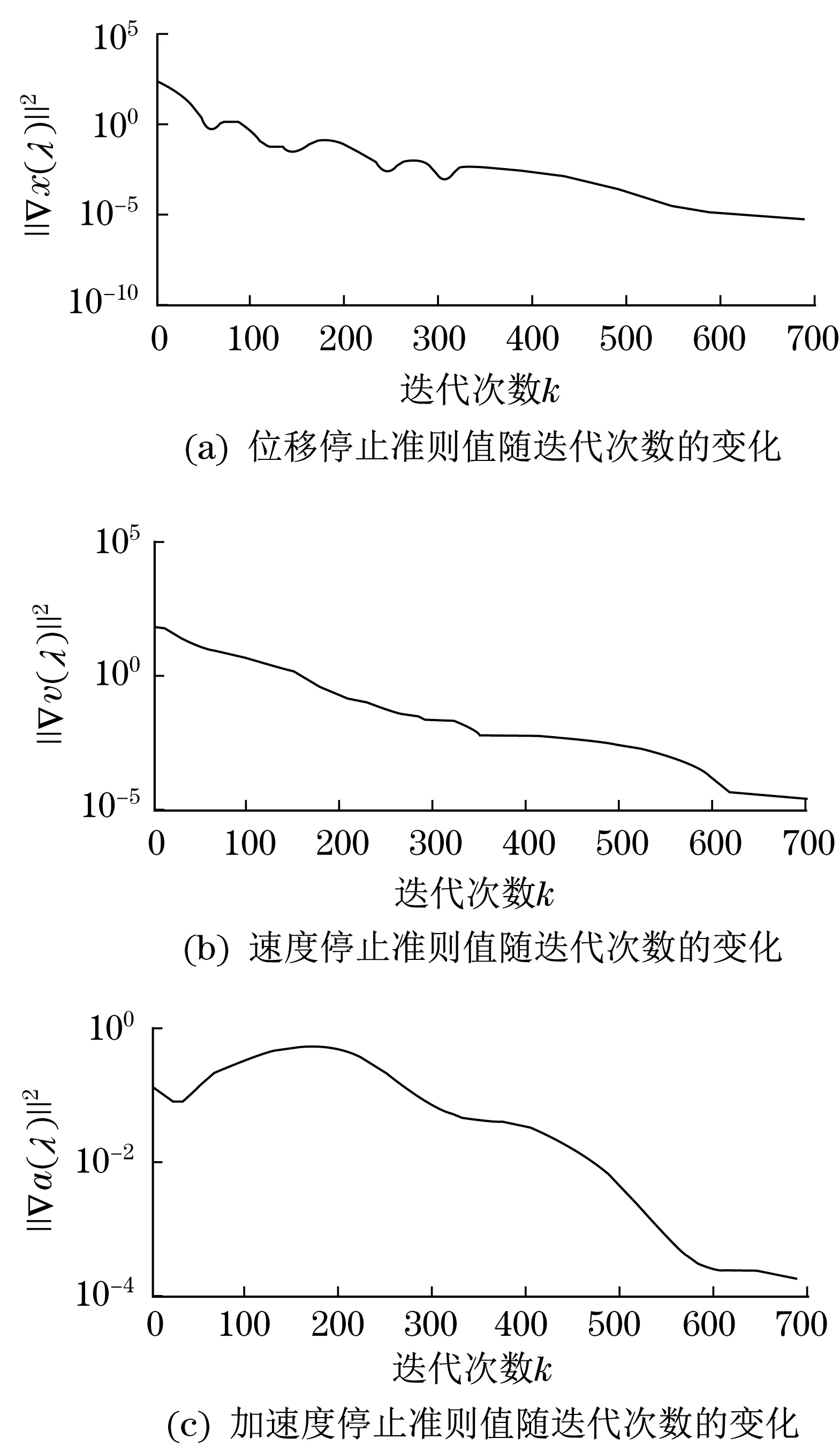
图2 分解的停止准则值随迭代次数的变化Fig.2 Relation between the separate stopping criterion values and iterations

虽然由‖ ∇d(λ)‖2提取分解的停止准则需要花费一些额外的流程时间，但可以灵活地设置3个不同的控制误差，这对于提高求解效率是非常有益的。

4.2 热起动迭代结果

对于车辆纵向运动控制，传感器的采样频率很高，两个连续的数据集之间的差别很小，可以选择前一数据集的最优解作为计算后一数据集最优解的一个初始估计，以减少迭代次数。用试验数据集对此热起动技术进行试验，停止准则为‖ ∇d(λ)‖2=10-2，采用和不用热起动的迭代结果比较，如图3 所示。若采用热起动技术，则可以显著地减少求解迭代次数，求解器性能可以得到很大改进。

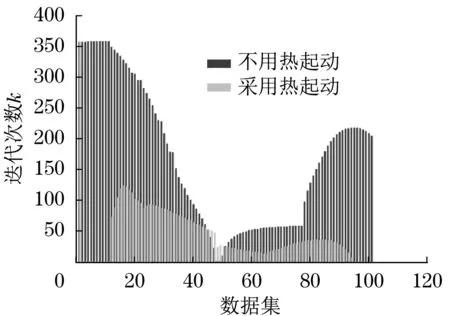
图3 采用和不用热起动的迭代结果Fig.3 Number of iterations for method with and without hot start

4.3 纵向运动控制跟踪结果

用试验数据集对采用前述各项技术开发的QP求解器进行试验，得到车辆纵向位移、速度和加速度的跟踪性能，如图4 所示。车辆纵向运动控制跟踪性能较好，可以满足预期要求。

图4 纵向位移、速度和加速度跟踪性能Fig.4 Tracking performance of the displacement，velocity and acceleration in longitudinal direction

5 结语

针对车辆自动驾驶纵向运动MPC 实现问题，建立了车辆纵向运动模型和纵向参考跟踪约束线性二次MPC 表达式；通过变量重排序和对MPC 表达式进行重构，建立了QP 模型，为优化求解约束MPC 问题时简化数值方法的实现打下了基础。采用拉格朗日松弛法将QP模型转化为包含两层优化问题的拉格朗日对偶问题，设计了求解该对偶问题的快速梯度法算法，对算法的参数进行了分析，并采用试验数据集对QP求解器进行了运行试验。通过分析和运行试验，明确了最小李普希茨常数、拉格朗日乘子初始值、热起动、综合和分解的停止准则，对求解器性能的影响和应用条件，验证了快速梯度法的有效性。开发的求解器，可以在车辆纵向运动控制采样率足够高的情况下实时运行。