不平衡及非线性负载下的三相逆变器控制方法

夏 翔，吴彬锋，朱利锋，王骏永，刘子卓，章寒冰

（国网浙江省电力有限公司丽水供电公司，浙江 丽水 323000）

0 引言

随着我国“双碳”（碳达峰及碳中和）目标和构建以新能源为主体的新型电力系统目标的提出，新能源在未来电力系统中扮演的角色将愈加重要。将本地分布式新能源与负荷等组织成微电网形式运行，可有效提高新能源消纳能力和利用效率，为重要负荷提供持续可靠供电，提高本地用户电能质量［1-6］。作为分布式电源与微电网接口的电力电子变流器及其控制成为当前的研究热点。在实际微电网系统中，大量的整流型非线性负载及不平衡负荷构成混合型负载。这类混合负载对微电网的稳定运行造成了诸多影响：非线性负载导致分布式电源输出电压波形畸变；不平衡负荷导致三相电压不对称度增加；半导体开关器件的热耐受力较低，导致系统过载能力较低。因此，需要先进的三相逆变器控制技术来保证在各种混合负载下，微电网内逆变型分布式电源仍然能够提供优质稳定的电能，并实现不对称过载故障下的故障穿越。

当三相逆变器带平衡和线性负载运行时，通常在同步旋转坐标系下采用PI（比例积分）控制，即可很好地跟踪电压参考值［7］。

在不平衡和非线性负载接入的情况下，三相三线制逆变器系统中将出现负序和谐波电压分量［8-12］，采用同步旋转坐标系中PI控制系统无法有效抑制负序和谐波电压分量。文献［13］在正序旋转坐标系中采用PIR（比例积分谐振）控制对负序分量进行抑制。文献［14-15］在正序与负序旋转坐标系分别实现PI 控制。文献［16-17］在正序旋转坐标系中采用PIR 控制，在静止坐标系中对零序分量采用PR（比例谐振）控制。文献［18］在正序旋转坐标系中对正负序分量、在静止坐标系中对零序分量均采用PID（比例积分微分）控制。上述方法需要进行坐标变换，采用电压-电流双环结构时控制器数量多，参数整定复杂。文献［19］提出了αβ坐标系下复变量谐振控制器，并通过线性二次型最优状态反馈优化控制参数。文献［20］提出一种αβ0 坐标系下的四桥臂逆变器控制策略，采用Quasi-PR（准比例谐振）控制输出电压，并加入参考电压前馈，改善系统控制精度与动态性能；该方法尽管简化了控制系统设计，但是仍然不能消除非线性负载所带来的谐波电压分量。为了降低非线性负载给逆变器输出电压带来的谐波含量，文献［21-23］在电压控制中增加3、5、7 次等谐波补偿控制环，该方法仅能消除特定频率的电压谐波分量，多谐振环节的设计导致计算运算资源占用较高。

围绕不平衡过载条件下逆变器的限流控制，文献［24］对比了不同限流方法防止限流锁定和积分饱和的相对能力。文献［25］阐述了不同限流方法在同步旋转坐标系、αβ0坐标系和自然坐标系中的适用性，提出了一种基于电流参考比例缩放的限流方法，但输出电流有效值的频繁计算需要存储大量采样数据，导致存储资源占用较高。

针对现有研究存在的问题，本文的主要工作可概括为：

1）提出一种适用于三相三线制逆变器的电压控制方法。该方法能够保证不平衡及非线性负载下的电压质量，运算及存储资源占用较小；实现过载故障的快速限流与故障切除后的快速恢复，且不影响正常相电压；电压控制采用单环结构，控制参数整定较为简单。

2）建立等效三相逆变器的传递函数模型，分析主要控制及硬件参数对系统稳定性的影响，为参数整定提供依据。

3）在PSCAD中搭建三相三线制逆变器仿真模型，并搭建5 kW三相三线制逆变器样机。通过仿真和实验，验证系统传递函数模型的准确性和所提控制方法的有效性。

1 三相逆变器结构

本文所研究的三相逆变器采用三相三线制结构，如图1所示，其中Lf和Cf分别为LC滤波器的滤波电感和滤波电容。三相三线制结构无法直接为单相负荷供电，可采用附加△/Y变压器等方法引出中线。当负荷为不平衡或非线性负荷时，对图1所示结构来说，电压控制目标是保证三相输出线电压对称。

图1 三相逆变器结构

2 三相逆变器控制策略

2.1 数学模型

图1 所示三相逆变器可以简化为图2 所示结构，其中uinv_abc为逆变器输出电压，n 为假想零电位点，n′为滤波电容中点。当逆变器采用SPWM（正弦脉宽调制）时，uinv_abc在一个开关周期内的平均值与调制参考电压eabc一致，即：

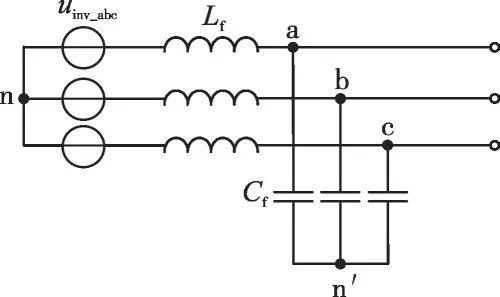
图2 三相逆变器等效电路

根据伏秒平衡原理，当一个开关周期前后电感电流的变化量可以忽略时，电感上的平均压降为0，可表示为：

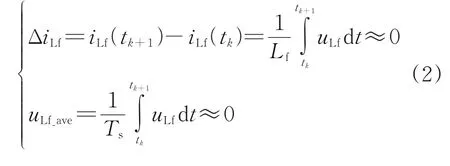
因此，认为uan=ea，ubn=ea，ucn=ec。由于调制参考电压三相对称，可以得到：

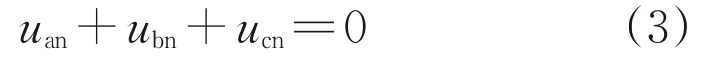
考虑到电容电压三相对称，有：

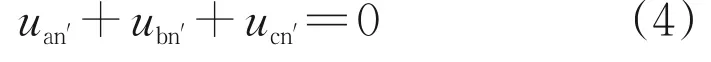
式（2）—（4）中：tk和tk+1分别为第k和第k+1 个开关周期的起始时刻；uLf_ave为一个开关周期内电感上的平均压降；ΔiLf为交流侧滤波电感电流平均值；iLf（tk）为第k个开关周期的起始时刻交流侧滤波电感电流瞬时值；uLf为交流侧滤波电感电压；Ts为一个开关周期的时间常数；uan、ubn、ucn为假想零电位点n的三相电压；ea、eb、ec为三相调制参考电压；uan′、ubn′、ucn′为滤波电容中点n′的三相电压；t为时间。

根据式（3）和式（4），可得点n 和n′间电压unn′=0。因此，将图1 中所示三相逆变器等效为3个单相电路进行分析，图3 为等效单相逆变器结构。图3中：uinv为等效单相逆变器输出电压；Zload为负载等效阻抗；iinv为滤波电感电流；io为负荷电流；iC为滤波电容电流；uo为等效负荷侧相电压。

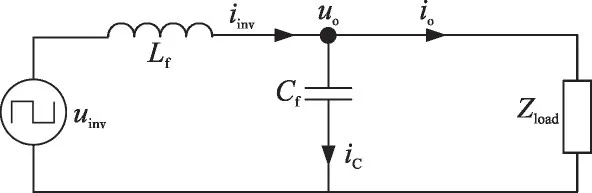
图3 等效单相逆变器结构

由图3可得等效单相逆变器的数学模型为：

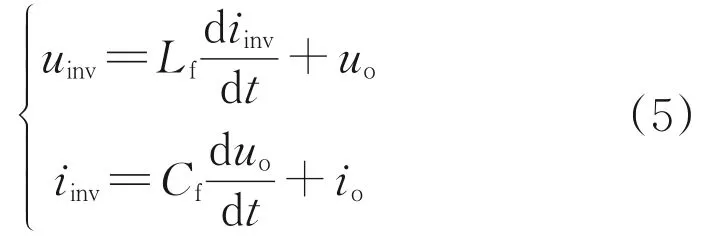
2.2 控制策略

本文所提出的电压控制策略在αβ坐标系下实现，电压控制框图如图4所示，其中：uref_αβ和uo_αβ分别为基波电压参考值和实际值；kp、kr、ωc、ω0分别为基波电压跟踪环节比例系数、积分系数、截止频率、谐振频率；krh和Th分别为谐波电压抑制环节的积分系数、滤波时间常数；Rv为限流环节虚拟电阻；Rd为有源阻尼环节虚拟电阻；upwm_αβ为输出的控制电压信号；s为拉普拉斯算子。

图4共包含4个部分：

图4 电压控制框图

1）基波电压跟踪。通常采用Quasi-PR 控制器，实现基波电压无静差跟踪。

2）谐波电压抑制。首先通过二阶广义积分器提取电容电压中的基频分量，然后进一步获取除基频分量外的其他分量，进行一阶滤波后反馈至调制电压。谐波电压抑制能够降低逆变器中频段的输出阻抗，对因非线性负荷引起的谐波电压进行负反馈控制。

3）输出限流。当系统发生短路故障或过载时对输出电流进行限制。

4）基于电容电流反馈的有源阻尼。通过模拟滤波电容串联电阻抑制LC 谐振，提高系统稳定性［26-30］。

与传统电压-电流双环控制相比，本文所提方法仅需电压环，简化了参数设计。在不平衡电压控制方面，由于控制在αβ坐标系下实现，无需进行正负序坐标转化；在谐波电压抑制方面，本文所提方法总体降低了变流器中频段输出阻抗，避免了传统方法中多谐振环节引起的运算资源消耗；传统电压-电流双环通过对电流环参考值进行限幅实现限流控制，当出现不平衡过载时将影响正常相电压，而本文所提控制策略能够确保限流过程中正常相电压不受影响。

为了实现限流功能，本文采用动态虚拟阻抗控制，其中动态虚拟阻抗的实现方法如图5 所示。图5中，采用SOGI（二阶广义积分环节）提取电感电流iinv在αβ坐标系的基频分量if及其正交分量ifq，计算相电流幅值Imag，避免通过计算有效值获取电流幅值需存储的大量采样数据。当检测到某一特定相电流幅值超过设定值Io时，通过PI 控制实现虚拟阻抗Rv的自适应，快速将该相电流幅值限制于Io。动态虚拟阻抗相当于在变流器与负载间接入了阻值为Rv的电阻，从而抑制了电流。过载故障清除后，该相电流幅值将低于Io，在原有Rv的作用下导致输出相电压幅值Uo升高，当检测到Uo超过U-IoRv时（U为额定电压幅值），将虚拟阻抗PI控制中的积分器复位，系统恢复至正常运行状态。

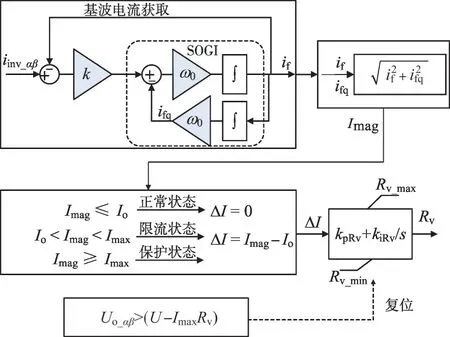
图5 动态虚拟电阻环节

由图4及LC 滤波器模型可得系统的传递函数模型为：

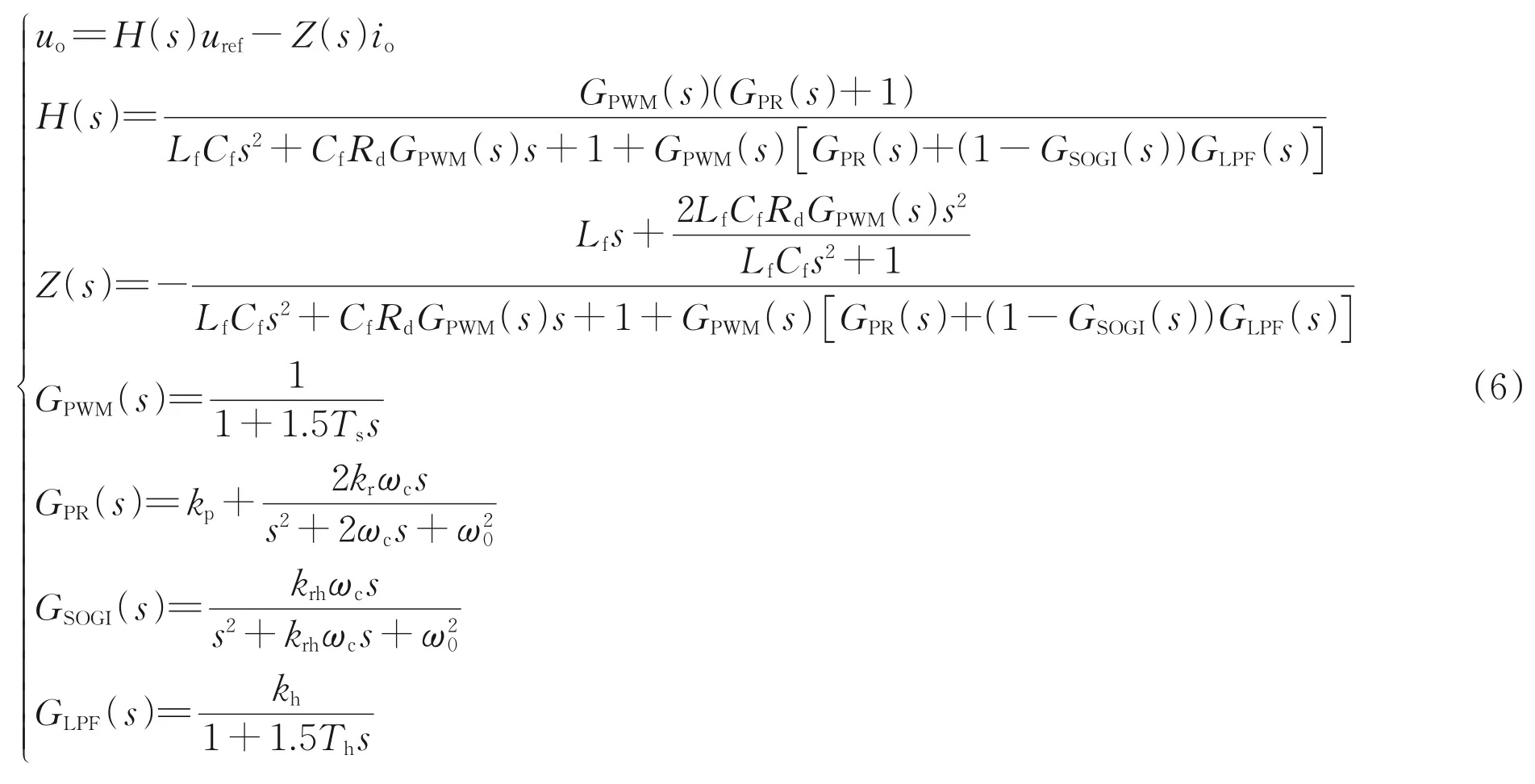
式中：H（s）为电压控制闭环传递函数；Z（s）为三相逆变器在考虑图4所示闭环电压控制后的等效输出阻抗。

2.3 稳定性分析

考虑系统基本参数如下：

1）主回路参数，Lf=2 mH，Cf=30 μF。

2）开关周期，Ts=100 μs。

3）Quasi-PR 控制器参数，kp=0.15，kr=2.5，ω0=314 rad/s，ωc=18 rad/s。

谐波电压控制参数kh大小不仅影响谐波电压抑制性能，且对系统稳定性影响也较大，因此着重通过分析kh变化时的系统闭环极点变化情况来研究系统稳定性。此外，还通过分析有源阻尼参数Rd、滤波时间常数Th以及LC 滤波参数在不同取值情况下对闭环极点的影响，来更加全面地分析影响系统稳定性的因素。

2.3.1 谐波电压控制参数kh和有源阻尼参数Rd对系统稳定性的影响

基于上述参数，kh以1 为步长从1 增大至10时，选择不同Rd，电压控制闭环传递函数H（s）的极点变化趋势如图6 所示。可以看出，随着kh增大，有一对高频共轭极点靠近虚轴移动，表明系统稳定性变差，易出现高频振荡失稳问题；随着Rd的增大，共轭极点向远离虚轴方向移动，系统稳定性增加。

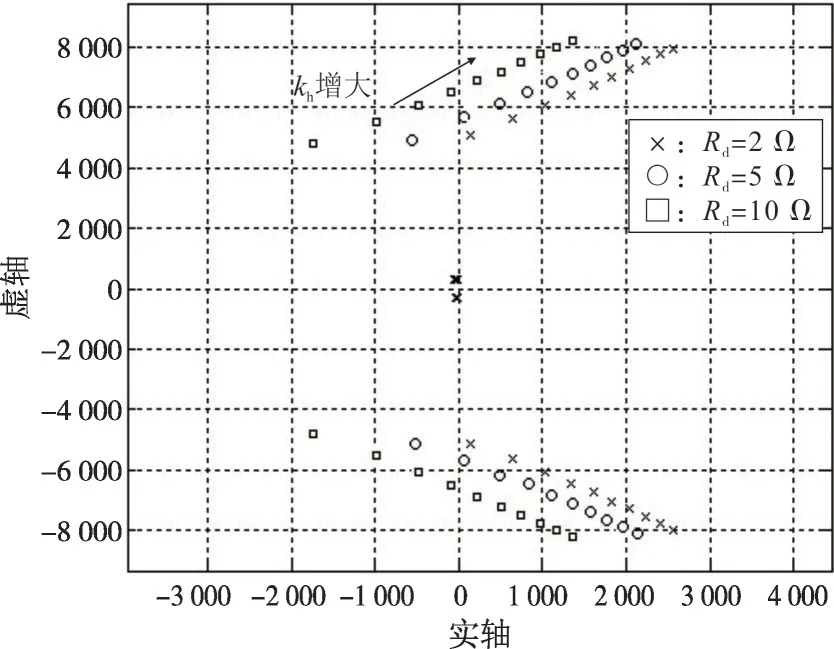
图6 不同Rd下的H（s）闭环极点

2.3.2 滤波时间常数Th对系统稳定性的影响

取Rd=10 Ω，在谐波电压控制中，不同滤波时间常数Th下，当kh以1为步长从1增大至10时，系统闭环极点变化趋势如图7所示。可以看出，增大Th可提高系统稳定性。

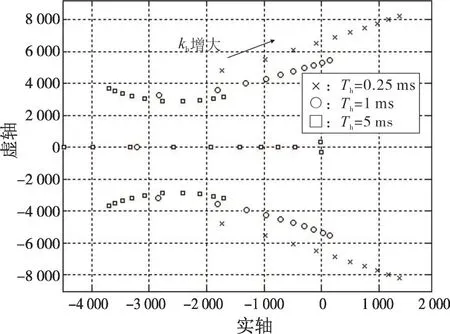
图7 不同Th下的H（s）闭环极点

不同Th下Z（s）的Bode 图如图8 所示，其中kh均取3。可以看出，中频段（ω0—11ω0，为电压谐波集中频段）内随着Th增大，谐波输出阻抗增大，即谐波电压抑制效果逐渐减弱。

2.3.3 LC滤波参数对系统稳定性的影响

不同滤波电容参数Cf下，当kh以1 为步长从1增大至10时，H（s）闭环极点变化趋势如图9所示。可以看出，为了保证系统稳定性，滤波电容量有最低要求。增大滤波电容量Cf，能够有效改善系统稳定性，但会导致成本和体积上升。

不同滤波电感参数Lf下，当kh以1 为步长从1增大至10 时，系统闭环极点变化趋势如图10 所示。可以看出，滤波电感量增大，不利于系统稳定性的改善。

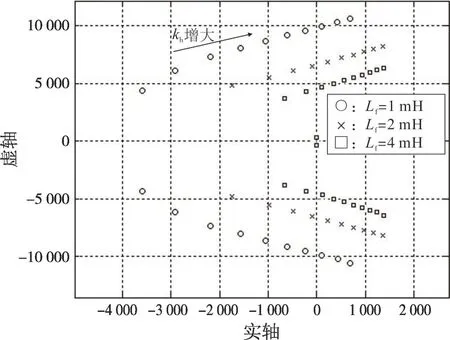
图10 不同Lf下的H（s）闭环极点

不同Lf下Z（s）的Bode图如图11中所示。可以看出，在中频段内，减小滤波电感量Lf，可以有效减小谐波输出阻抗，有利于增强谐波电压抑制效果。

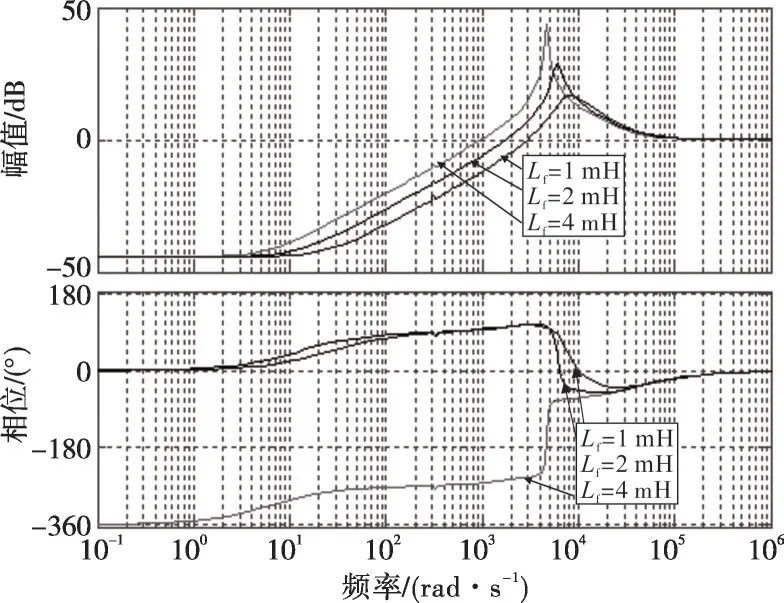
图11 不同Lf下Z（s）的Bode图

3 仿真验证

为了验证本文传递函数模型的正确性和控制方法的有效性，在PSCAD 软件中搭建如图12 所示三桥臂逆变器仿真模型。其中非线性负荷为整流性负荷，直流侧电阻为60 Ω，线性负荷为AC相间阻性负荷40 Ω，直流侧电压为300 V，交流电压参考值uref幅值为100 V（即相电压幅值100 V，线电压幅值为173 V）。在仿真工况中，除额外声明，逆变器硬件回路与控制环节参数与表1一致。

图12 三相逆变器仿真模型

表1 仿真系统参数

3.1 稳定性分析验证

3.1.1 有源阻尼参数Rd对系统稳定性的影响

选择kh=5，Rd=2 Ω，仿真结果如图13 所示（在t=0.2 s投入闭环控制）。可以看出，系统出现了高频谐振失稳，与图6理论分析相吻合，即在谐波电压控制参数kh较大，且有源阻尼电阻较小时，容易出现高频振荡失稳。

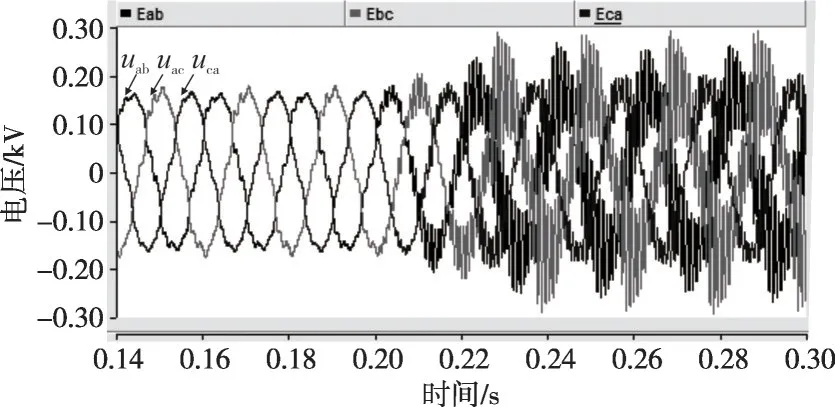
图13 线电压（kh=5，Rd=2 Ω）

将有源阻尼电阻Rd增大至10 Ω，仿真结果如图14—16 所示。可以看出，增大有源阻尼电阻能有效提高系统稳定性。电压三相不平衡度得到改善，THD（电压总谐波失真）从10.5%降至3.5%左右，表明所提方法能有效解决不平衡及非线性负荷带来的输出电压不平衡和谐波问题。根据图16 中对线电压进行的FFT（快速傅里叶变换）分析，线电压谐波主要集中在5、7、11、13、17、19倍基频附近。

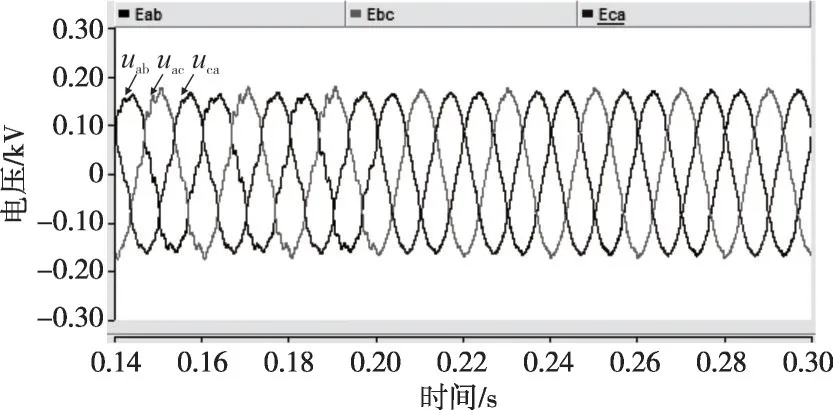
图14 线电压（kh=5，Rd=10 Ω）

3.1.2 滤波时间常数Th对系统稳定性的影响

当Th=5 ms 时，仿真结果如图17—18 所示。对比图15和图18，可以看出当滤波时间常数Th增大后，电压THD 从10.5%降至7.5%左右，而图15中电压THD则降至3%左右，这表明增大滤波时间常数会削弱谐波电压抑制效果，与图7理论分析相吻合。

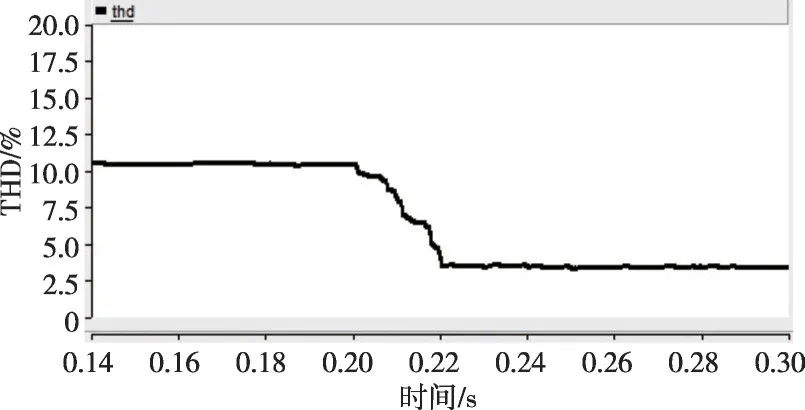
图15 线电压THD（kh=5，Rd=10 Ω）

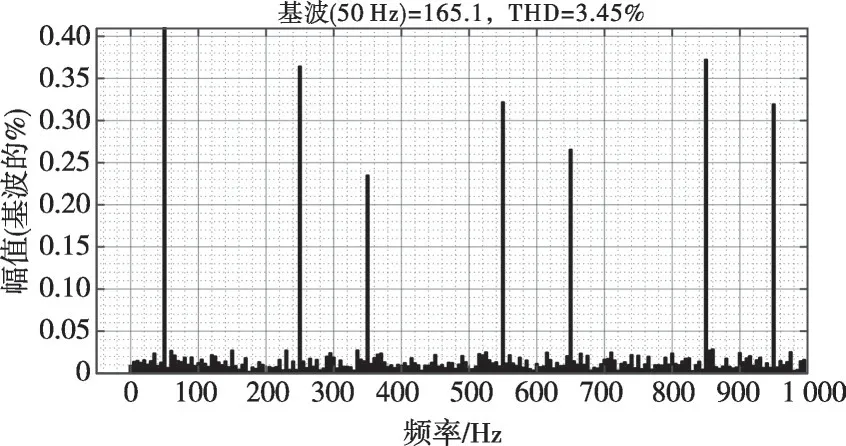
图16 线电压FFT分析

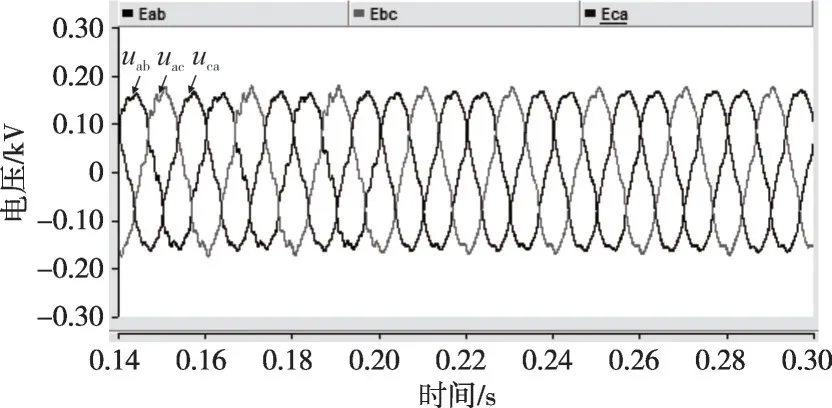
图17 线电压（Th=5 ms）

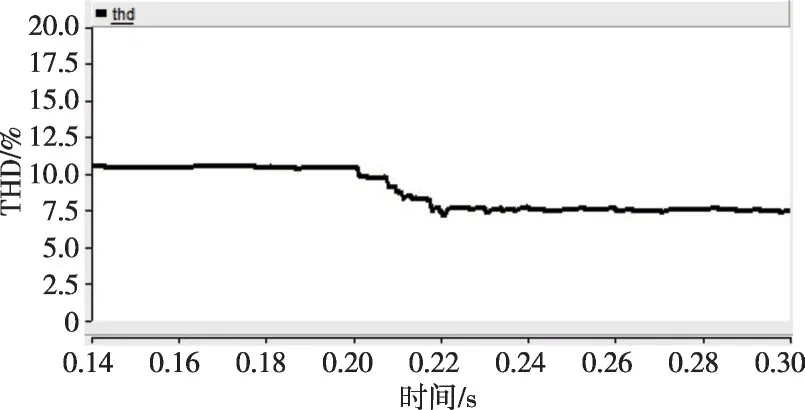
图18 线电压THD（Th=5 ms）

3.1.3 LC滤波参数对系统稳定性的影响

选择Cf=10 μF，仿真结果如图19所示（在t=0.2 s投入闭环控制）。可以看出系统出现了高频谐振失稳，这表明滤波电容减小，系统稳定性变差，与图9中理论分析相吻合。

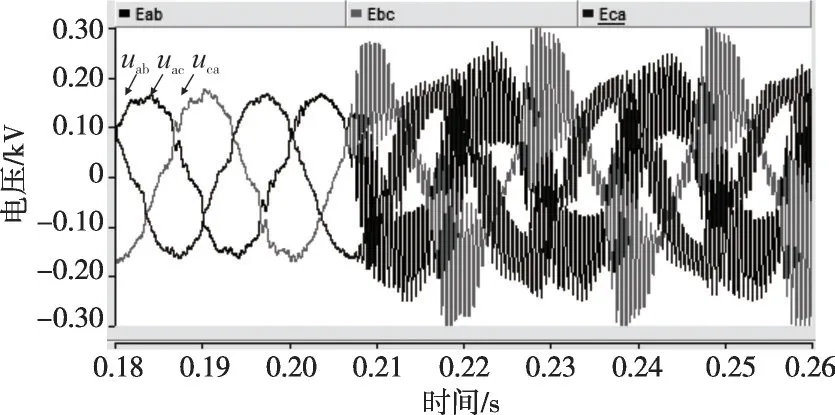
图19 线电压（Cf=10 μF）

选择Cf=30 μF，仿真结果如图20所示（在t=0.2 s投入闭环控制）。可以看出系统稳定运行，但输出电压仍存在高频振荡分量。

将滤波电感Lf减小至1 mH，仿真结果如图21—22所示。对比图20和图21可知，减小滤波电感后，能有效提高系统稳定性。对比图15和图22可知，电压THD 进一步减小。上述仿真结果与图9—10中理论分析相吻合。

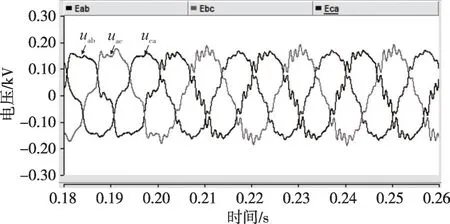
图20 线电压（Cf=30 μF）

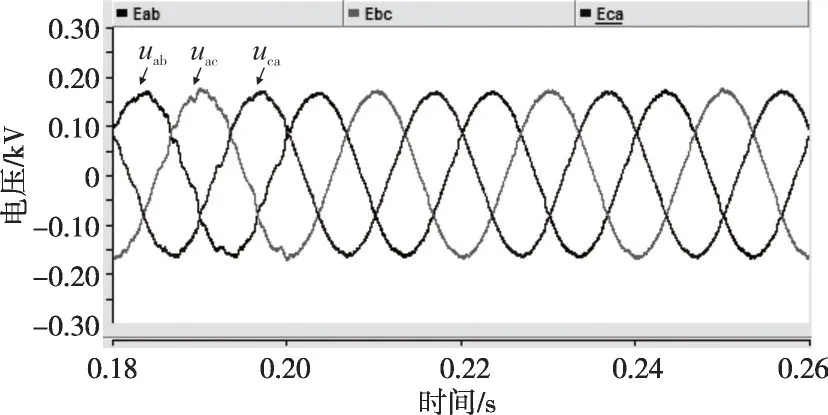
图21 线电压（Lf=1 mH）

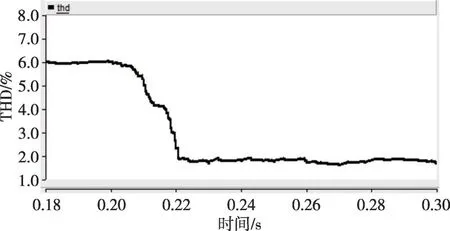
图22 线电压THD（Lf=1 mH）

3.2 控制策略验证

3.2.1 负荷突变工况

经过上述理论分析，选择谐波电压控制器参数kh=3，Th=0.25 ms，有源阻尼电阻Rd=10 Ω。在t=0.25 s时，相间负荷电阻从40 Ω突变为20 Ω；在t=0.3 s时，三相整流桥直流侧电阻从60 Ω突变为30 Ω，仿真结果如图23—26所示。

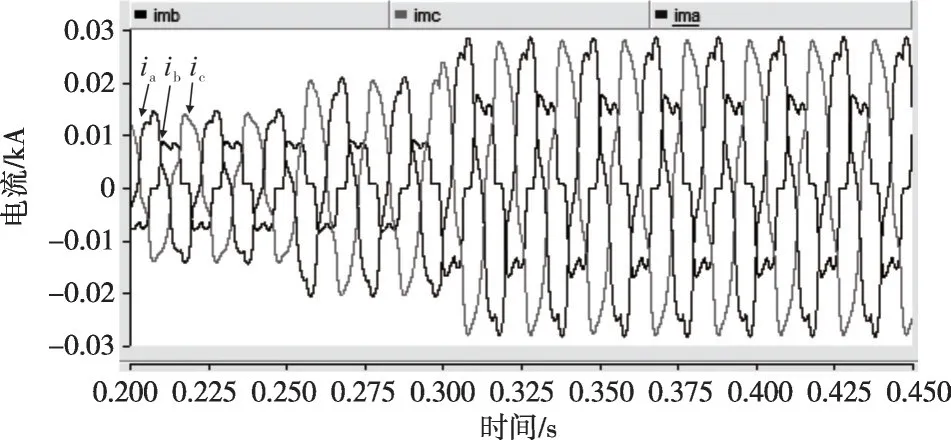
图23 负载电流

从仿真结果可以看到，在不平衡和非线性负荷突变情况下，本文所提控制方法均能有效保证三相电压的电能质量。采用VUF（电压不平衡度评价指标）如式（7）所示，在整个暂态过程中VUF小于0.4%。非线性负荷增大后，电压THD 稍有提高，但仍控制在5%以内。

图24 线电压

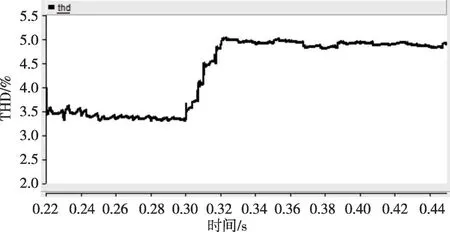
图25 线电压THD

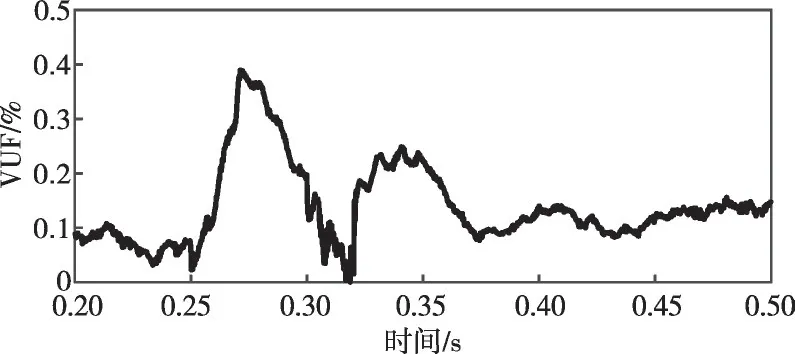
图26 线电压VUF

式中：bVUF为VUF的值；|u+|为正序电压幅值；|u-|为负序电压幅值。

3.2.2 限流功能验证

分别验证不平衡负荷以及非线性负荷投入情况下，本文所提限流方法的有效性。

1）工况1：在t=0.25 s 时，相间负荷电阻从40 Ω 突变为5 Ω；在t=0.3 s 时，投入输出电流限流控制（限流值为30 A），仿真结果如图27—29所示。

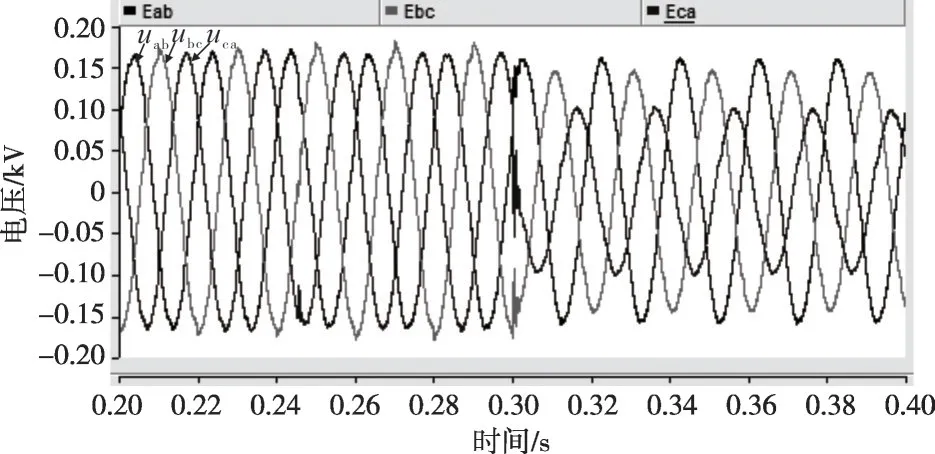
图27 线电压（工况1）

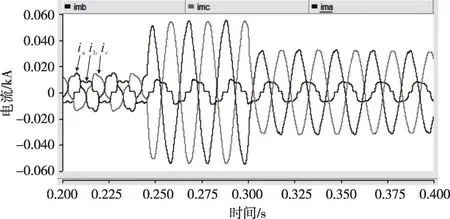
图28 负载电流（工况1）

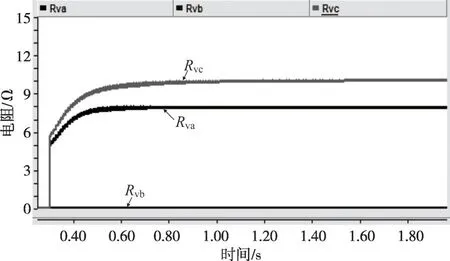
图29 动态虚拟电阻（工况1）

2）工况2：在t=0.25 s时，三相整流桥直流侧电阻从60 Ω突变为15 Ω；在t=0.3 s时，投入输出电流限流控制（限流值为30 A），仿真结果如图30—32所示。

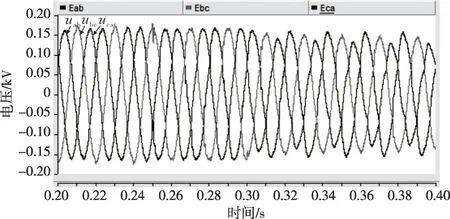
图30 线电压（工况2）

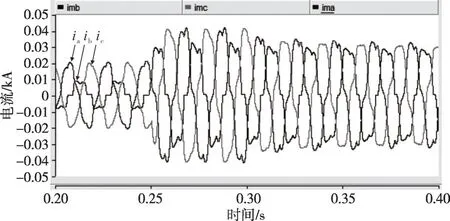
图31 负载电流（工况2）

图32 动态虚拟电阻（工况2）

从仿真结果可以看到：t=0.3 s 之前未启动输出电流限流控制时，由于负荷突然增大导致输出电流幅值增大至50 A 左右；t=0.3 s 投入控制后，电流迅速降至30 A 左右。由于限流作用，输出电压不能再保证平衡。

4 实验验证

4.1 实验系统

为了验证本文所提三相逆变器控制方法的有效性，搭建如图12 所示的5 kW 三相逆变器样机。直流侧电压为300 V，交流侧相电压幅值参考值为100 V，输出经220 V/380 V 隔离变压器连接不平衡和非线性负载，硬件回路和相关控制参数如表2所示。

表2 硬件回路及控制参数

4.2 工况实验

4.2.1 不平衡负荷突变工况

负荷情况为：AB 相间电阻40 Ω，通过投切BC相间电阻60 Ω来模拟不平衡负荷突变工况。图33—34为在开环控制（即未投入本文所提出的电压控制方法）情况下的不平衡负荷投切实验波形；图35—36 为在投入本文所提出的电压控制方法情况下的不平衡负荷投切实验波形。

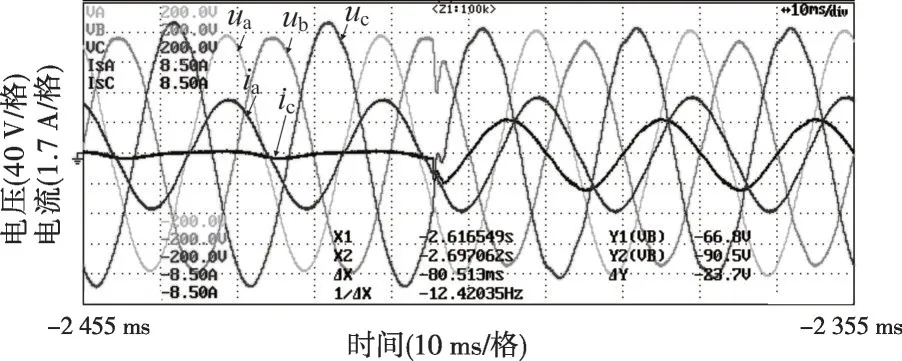
图33 不平衡负荷投入实验波形（开环控制）

对比上述实验结果可知，本文所提控制方法能够有效解决不平衡负荷所带来的问题，在不平衡负荷突变情况下能够保证三相电压平衡。

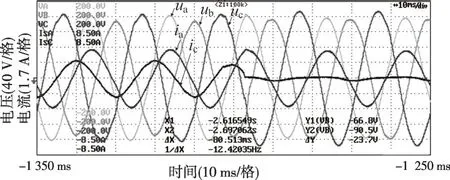
图34 不平衡负荷切除实验波形（开环控制）

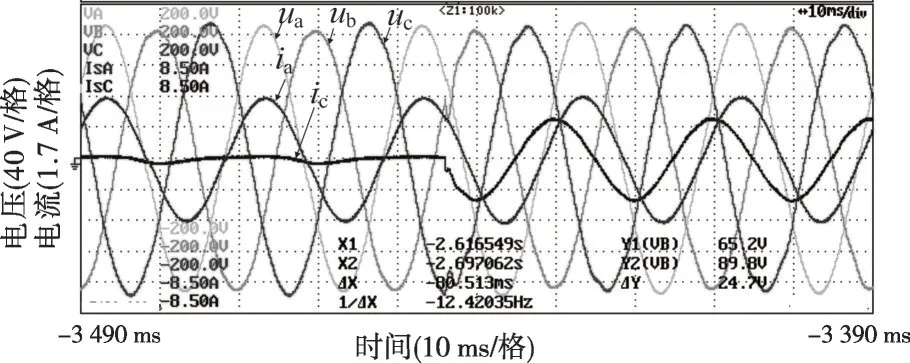
图35 不平衡负荷投入实验波形（本文方法控制）

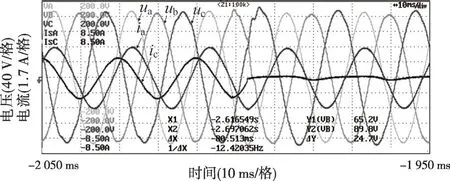
图36 不平衡负荷切除实验波形（本文方法控制）

为了验证限流效果，将相电流限流幅值设置为15 A，不平衡负荷投切实验波形分别如图37—38 所示。可以看到：不平衡负荷增加后，逆变器输出限流，导致逆变器输出三相电压不平衡；负荷切除后，逆变器退出限流运行状态，电压控制效果恢复，三相电压输出平衡。

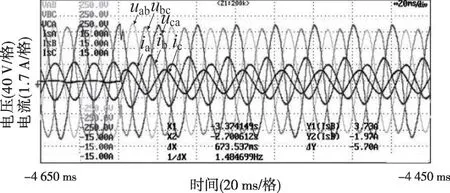
图37 不平衡负荷投入实验波形（限流15 A）

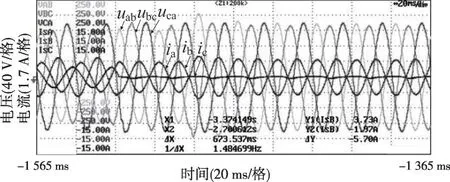
图38 不平衡负荷切除实验波形（限流15 A）

4.2.2 不平衡和非线性负载工况

负荷情况为：AB 相间电阻20 Ω，BC 线间电阻60 Ω，非线性负荷采用三相整流桥，直流侧电阻为120 Ω。图39—40为在开环控制情况下的实验波形；图41—42 为在投入本文所提的电压控制方法情况下的实验波形。

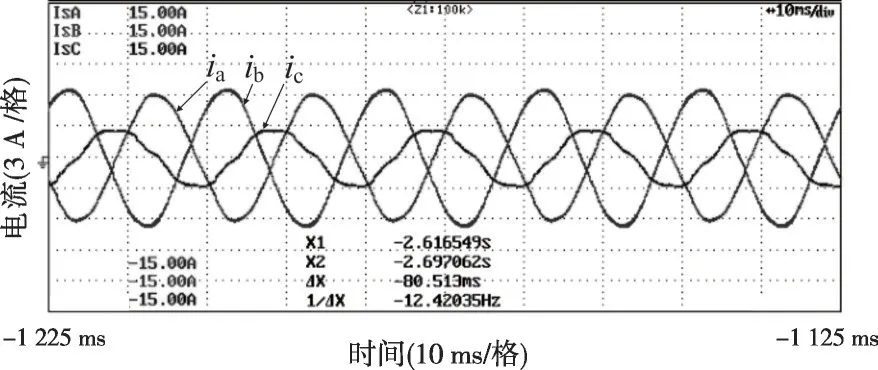
图40 不平衡和非线性负载实验电流（开环控制）

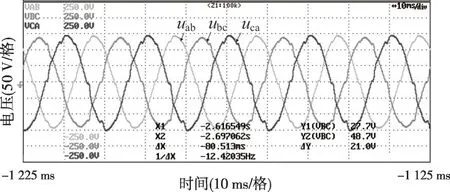
图41 不平衡和非线性负载实验线电压（本文方法控制）

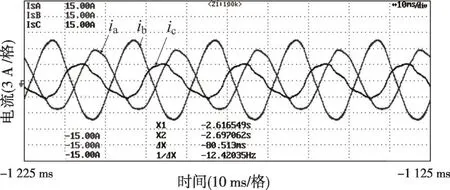
图42 不平衡和非线性负载实验电流（本文方法控制）

对比上述实验结果可知，本文控制方法能够有效解决不平衡和非线性负载带来的问题，提高复杂运行工况下逆变器输出电压波形和电能质量。

5 结语

围绕混合负载下逆变器的运行问题，本文提一种三相逆变器控制方法。该方法的优势在于：能够在不平衡和非线性负载条件下保证逆变器端电压质量；实现不平衡过载故障的快速限流与故障切除后的快速恢复，且不对正常相电压造成影响；电压控制采用单环结构，控制参数整定较为简单；避免了多谐振补偿环节及有效值计算造成的运算和存储资源增加，易于硬件实现。

本文建立了逆变器系统传递函数模型，对主要硬件回路及控制参数对系统稳定性的影响进行了讨论，实际参数整定中应综合考虑系统稳定性、谐波抑制能力与硬件成本和体积。当微电网中多逆变器并联运行时，如何实现过载故障的协同限流是后续研究的重点。