保序回归算法的MATLAB实现

2022-03-21刘瑞银周志慧

沈阳师范大学学报(自然科学版) 2022年6期

刘瑞银, 周志慧, 杜欢

(沈阳师范大学数学与系统科学学院, 沈阳 110034)

0 引言

20世纪中叶以来,序约束下的统计推断在统计分析中占有十分重要的地位,至今已建立了较为完善的理论[1-2]。在这一领域中,通常研究序约束下求解未知参数的极大似然估计。然而,传统的极大似然估计所得到的结果会使总体均方误差相对较大,缺点明显。文献[3-5]中指出,保序回归和一般的极大似然估计相比,具有较小的总体均方误差。因此,研究保序回归很有意义。

保序回归在生物医学方面应用广泛。在药物剂量反应中,随着体内药物剂量或浓度的增加,药效和药物的毒性也会随之增加。由于某些药物具有毒副作用,因而就会使得药效呈现一种先升后降的伞型趋势。可以利用每个剂量水平下病人毒性反应的比率来估计不同剂量水平下的毒性概率[6],但是这种情况下所估计出的毒性概率可能不是剂量水平的非减函数,此时可以采用保序回归方法来解决这个问题。

1 保序回归

假设某种药物的使用剂量为X,病人对该药物的反应值为Y,剂量的取值范围为1,2,…,100,对应的真实反应值为Y=y1,y2,…,y100。正常情况下随着药物使用剂量的增加,病人对药物的反应值也应该增加,但由于病人个体的原因,Y不一定是一个非减函数。如果按照药物的真实反应排序,对应的X将会成为乱序,从而失去了研究意义。本文研究目的就是为了观察随着药物使用剂量的增加,病人的平均反应状况也得到相应序约束的变化。在这种情况下,利用保序回归,可以在不改变X排列顺序的条件下,得到满足序约束关系的Y。

1.1 常见的半序关系

定义1[7]设Θ={θ1,θ2,…,θk}为有限集合,称集合Θ上的一个关系“≤”为半序,如果满足下列关系:

1)θi≤θj; 其中θi∈Θ;

2) 如果θi,θj,θk∈Θ,θi≤θj,θj≤θk,那么θi≤θk;

3) 如果θi,θj∈Θ,θi≤θj并且θj≤θi,那么θi=θj。

常见的半序关系有以下几种形式:

简单半序:θ1≤θ2≤…≤θk;

伞型半序:θ1≤…≤θh≥…≥θk;

简单树半序:θ1≤θj,j=2,…,k;

简单环半序:θ1≤θj≤θk,j=2,…,k-1;

其中简单半序是伞型半序当h=k时的一种特殊情况。

1.2 保序回归的定义

定义2 对于定义于Θ上的函数y=(y1,y2,…,yk)T,其中yi=y(θi),如果θi,θj∈Θ,θi≤θj,有y(θi)≤y(θj),则称函数y为对于“≤”的保序函数[8]。

定义3 假定G是保序函数的全体,给定函数g=(g1,g2,…,gk),ω=(ω1,ω2,…,ωk)T是一个给定的权函数,其中ωi>0,i=1,2,…,k。如果函数g*∈G且满足式(1)

(1)

则称函数g*为(g,ω)的保序回归[9]。

2 保序回归的算法步骤

本节主要介绍求简单半序和伞型半序的保序回归的算法步骤,其他半序的算法可以通过简单半序和伞型半序算法的相应变换得到。假设Θ={θ1,θ2,…,θk}是一个有限集合,G是保序函数的全体,g和ω为给定函数和权函数。首先考虑简单半序:θ1≤θ2≤…≤θk,以下求简单半序保序回归的算法名为PAVA(pool-adjacent-violators)算法[10-11]。

2.1 PAVA算法步骤

步骤1 如果g∈G,则g*=g。

步骤2 如果g∉G,则必定存在一个下标i,有gi-1>gi。令B={i-1,i},则

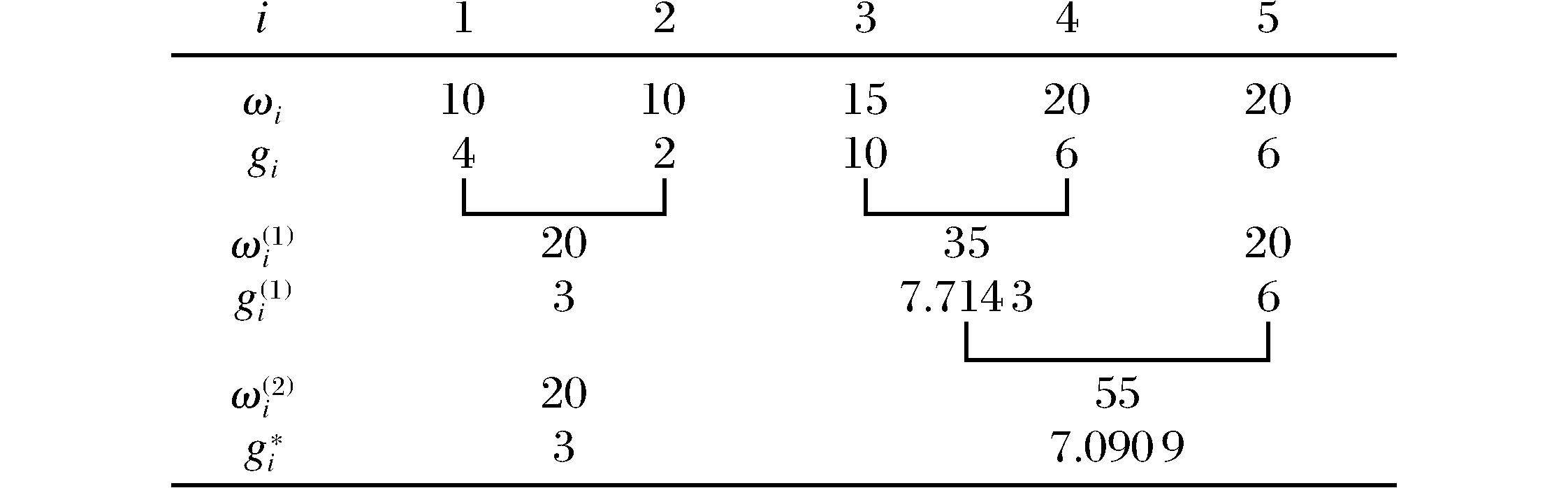
图1 简单半序保序回归的计算过程Fig.1 Calculation process of simple isotonic regression

例1[12]设i={1,…,5},给定g=(4,2,10,6,6),ω=(20,10,10,15,20),求出g简单半序的保序回归g*。计算过程如图1所示。

其中3=(10×4+10×2)/(10+10);7.090 9=(35×7.714 3+20×6)/(35+20)。因为3<7.090 9,所以g*=(3,3,7.090 9,7.090 9,7.090 9)。

下面介绍伞型半序保序回归的算法[13]。本文中介绍伞型半序的其中一种形式----先降后增,h点为最小值点时的情况。伞型半序的形式为θ1≥…≥θh≤…≤θk,h对应伞型的最小值点,当h=1或h=k时,伞型半序变为简单半序。

2.2 伞型半序的算法步骤

步骤1 如果g∈G,则g*=g。

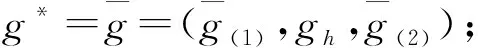
步骤5 重复步骤4,直到包含h的块的加权平均数比其他所有数都小为止。

例2 设k={1,…,9},h=4,给定g=(10,8,9,6,4,7,6,8,9),ω1=…=ωk,求出g的伞型半序的保序回归g*。

首先对(10,8,9)和(4,7,6,8,9)使用PAVA算法。

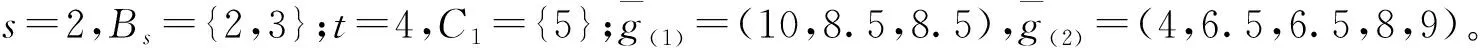
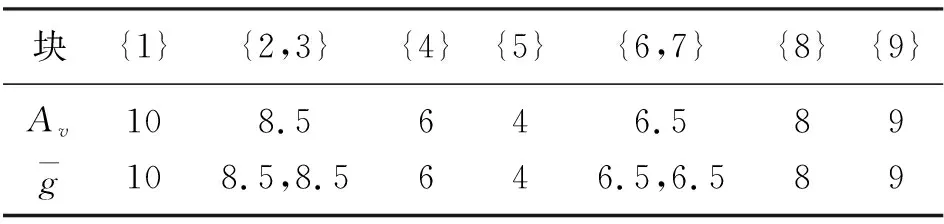
表1 伞型半序保序回归的计算过程(a)

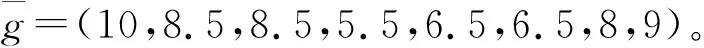
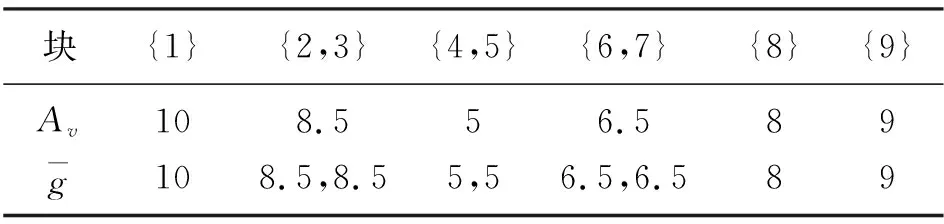
表2 伞型半序保序回归的计算过程(b)

以上介绍了简单半序与伞型半序的算法步骤,其他半序的算法可以通过简单半序和伞型半序算法的相应变换得到。下面对2种算法进行程序实现。

3 程序实现

3.1 简单半序的算法实现

利用MATLAB软件,编写一个名为Iso的函数解决简单半序型均值的估计问题[14-15]。Iso函数的程序代码如下:

function is=Iso(a,w)

n=length(a); is=zeros(1,n);uu=0;

while (uu

v=uu+1;b=cumsum(a(v:n).*w(v:n));d=cumsum(w(v:n));b=b./d;u=min(b);

m=find(b==u);m=m(1)+v-1; is(v:m)=u;uu=m;

end

其中:a表示待排序的变量;w表示对应的权重。这里继续考虑实例1中的问题,在命令窗口中输入:a=[4 2 10 6 6];w=[10 10 15 20 20]; iso(a,w)

则输出的结果为

ans=3.000 0 3.000 0 7.090 9 7.090 9 7.090 9

这与图1中的结果是一致的。

3.2 伞型半序的算法实现

利用Iso函数编写一个名为Umb的函数计算伞型半序的保序回归。Umb函数的程序代码如下:

functiona=Umb(x,w,h)

k=length(x);b=-x(1:(h-1));b=Iso(b,w(1:(h-1)));b=-b;a=x((h+1):k);

a=Iso(a,w((h+1):k));u=[b,a]; [u,INDEX]=sort(u);v=INDEX;ww=[w(1:(h-1)),w((h+1):k)];

fori=1:(k-1)

www(i)=ww(v(i));

end

ww=[w(h),www];a=[x(h),u];ap=cumsum(a.*ww);wp=cumsum(ww);dd=ap./wp;

d=min(dd);m=find(dd==d);

if(m(1)==k)

a=linspace(d,d,m(1));

else

a=[linspace(d,d,m(1)),a((m(1)+1):k)];

fori=1:(k-1)

u(v(i))=a(i+1);

end

a(1:(h-1))=u(1:h-1);a(h)=d;a((h+1):k)=u(h:(k-1));

end

其中:a表示待排序的变量;w表示对应的权重;h表示最小值点。在这里考虑实例2中的问题,在命令窗口中输入:

x=[10 8 9 6 4 7 6 8 9];w=[1 1 1 1 1 1 1 1 1];h=4; Umb(x,w,h)

则输出的结果为

ans=10.000 0 8.500 0 8.500 0 5.000 0 5.000 0 6.500 0 6.500 0 8.000 0 9.000 0

这与表2中的结果是一致的。

4 在基因计算中的应用

利用寡核苷酸阵列和c-DNA阵列可以获得基因的表达数据,利用获取的数据可以发现人们感兴趣的信息。本研究小组收集了1 900个基因在6个不同时间点的表达情况的数据,研究这1 900个基因的表达模式,对于一些表达模式相似的基因,它们的功能也是大同小异的。反过来思考,如果有2个基因被同一个调控系统控制着,那么可以认为它们的表达模式是相类似的。

为了进行基因选择,在研究过程中,首先要选定几种感兴趣的基因表达曲线模式,通过对观测到的数据进行计算,把表达模式属于选定曲线模式的基因挑选出来。常见的基因曲线模式有平凡曲线模式、简单序曲线模式、伞状序曲线模式、循环曲线模式和分段不等式曲线模式等,然后通常要求出基因在每个模式下的均值的估计值。本文所提出的PAVA算法就可以解决这个问题。

基于本文研究,为了进行基因选择,便于后续多重假设检验技术的研究,对ORIOGEN算法进行了调整,改进后的算法如下:

第1步选取曲线模式,将表达曲线模式记为C1,C2,…,Ch。对每个基因g=1,2,…,G重复进行下述步骤。

第2步利用PAVA算法求出基因在每个模式Ci,i=1,2,…,h下的均值的估计值。