河道水面线推求方法比较

王文浩

（长治市水文水资源勘测站 山西长治 046000）

在开展山洪灾害评价工作中，通过山洪灾害调查，详查了沿河村落的重点河道治理情况。一些沿河村落的河道行洪能力较差，沿河村落受到不同程度的洪水灾害，给人民的经济财产等造成了不同程度的损害。河道治理工作中的一个重要环节就是水面线的推求，对于一些无监测资料的河道，水面线的推求方法显得尤为重要。

1 水面线方法介绍

水面线的推求方法有许多，山洪灾害中沿河村落河道长度较短，水流流态稳定，一般采用水力学方法和曼宁公式进行计算。

1.1 水力学方法

水力学方法采用Godunov 格式[1]的有限体积法建立的复杂明渠水流运动的高适用性数学模型计算[2]。

1.1.1 控制方程

描述天然河道一维浅水运动控制方程的向量形式如下：

式中B为水面宽度，Q为断面流量，Z为水位，A为过水断面面积，α 为动量修正系数，一般默认为1.0，f1和f2分别代表向量F（U）的两个分量，g为重力加速度，t为时间变量，J为沿程阻力损失，其表达式为J=（n2Q|Q|）/（A2R4/3），R为水力半径，n为糙率。

浅水方程的以上表达形式在工程上应用较广，源项部分采用水面坡度代表压力项的影响，其优点是水面变化一般比河道底坡变化平缓，因此即使底坡非常陡峭时，对计算格式稳定性的影响也不大。另外该形式还可以很好的避免由于采用不理想的底坡项离散方法平衡数值通量时所带来的水量不守恒问题。

1.1.2 数值离散方法

采用中心格式的有限体积法，把变量存在单元的中心，如图1所示。

图1 中心格式的有限体积法示意图

将公式（1）在控制体i进行积分并且运用Gauss定理进行离散后得到公式（2）：

式中：Ui为第i个单元变量的均值；为单元i左右两侧界面通量值；Δxi为第i个单元边长；Si为第i个单元源项均值。

1）HLL 格式的近似Riemann 解

对界面通量计算采用HLL（Harten，Lax，vanLeer）格式，HLL 格式求解形式简单，处理干单元时的功能优于其它格式，通量求解过程如公式（3）：

式中sL和sR为计算单元左右两侧波速，当sL≥0 和sR≤0 时，计算单元界面的通量值分别由其左右两侧单元的水力要素确定，当sL≤0≤sR时，计算单元界面通量由HLL 近似Riemann 解给出[3]。

经过离散后，公式（2）中的连续方程变为如公式（4）：

可以看出，式中变量Q被通量f1取代后，由于通量f1可以保持良好的守恒特性，但是变量Q不具备守恒特点，因此，为保持计算格式的和谐性，Ying 等提出采用通量f1的值取代输出结果中的Q值，而由动量方程计算得出的Q值仅作为计算Riemann 问题的中间变量[4]。

2）二阶数值重构

采用HLL 格式近似Riemann 解求解，界面通量在空间上具有一阶精度，为使数值解的空间精度能够提高到二阶，界面左右两侧的变量采用MUSCL 方法进行数值重构，其表达式为：

式中：ri=（Ui+1-Ui）/（Ui-Ui-1），ri+1=（Ui+1-Ui）/（Ui+2-Ui+1）。φ 为限制器函数，本文采用应用较为广泛的Minmod 限制器，该限制器可以使格式保持较好的TVD 性质[5]。

为了保持数值解提高到二阶精度，并维持数值解的稳定性，对时间步用Hancock 预测、校正的两步格式：

3）源项的处理

源项包括水面梯度项和摩阻项。其中摩阻项采用显格式进行处理。水面梯度项的处理是为了保持公式中数值解的光滑性，使用空间数值重构后的水位变量值计算式中水面梯度，表达式如公式（7）：

1.2 曼宁公式

根据曼宁公式（式8）推求河道各个横断面的不同水位对应的流量，可以得到水位流量关系，然后采用插值法求出各横断面的不同频率流量下对应的水位，得到沿河村落水面线成果。

式中，A为过水断面的面积，m2；v为断面的平均流速，m/s；R为过水断面水力半径；J为水面的比降；n为河道断面糙率。

2 实例

选取有实测资料的河道进行水位计算，对比曼宁公式和水力学两种方法计算精度。

2.1 河道概况

孔家坡河道位于沁源县沁河镇孔家坡村沁河上，属黄河流域沁河水系。选取主河道河段长度为1.5 km，主河道纵坡6.0‰，河段间无支流汇入。

2.2 水文站概况

孔家坡水文站是黄河流域沁河水系沁河上的第一站，地处太岳山腹心，为黄河流域沁河水系沁河的发源地，属华北黄土高原的一部分。地形西北高，东南低，最高处为太岳山主峰伏牛角鞍，海拔2 523 m，最低处是县境南端的沁河河谷，海拔939 m。境内山恋起伏，沟壑纵横，该站是沁源、安泽、沁水、阳城等各县市区的重要防洪依据站，同时也是探索、研究和分析太岳林区各种水文特征、暴雨径流、雨水墒情及产汇流关系的区域代表站。孔家坡水文站设立于1958年6月1日，1962年3月基本水尺断面下迁25 m，称孔家坡（二）站，站址位于沁源县沁河镇孔家坡村沁河干流上，控制流域面积1 358 km2，断面以上主河道长度69.3 km，主河道纵坡6.0‰，流域形状系数0.283。由于河道冲刷、淤积等原因，河道断面变化较大，对模型计算结果具有一定的影响，因此选取孔家坡水文站2016年7月18日至8月28日水情资料进行模型计算。

2.3 计算结果

1）曼宁公式

采用曼宁公式推出河道上游断面水位值，与实测水位资料进行对比，结果见表1。

表1 水位值对比分析

2）水力学方法

采用水力学方法计算河道上游断面水位值，与实测水位资料进行对比，结果见表2。

表2 水位值对比分析

3）对比分析

选取2016年洪水资料，洪水最大流量为350 m3/s，采用曼宁公式计算断面过水能力2 700 m3/s。此次洪水流量小于河道过水能力，采用水力学方法计算不需要考虑漫滩情况。对比两种方法计算结果见表3。

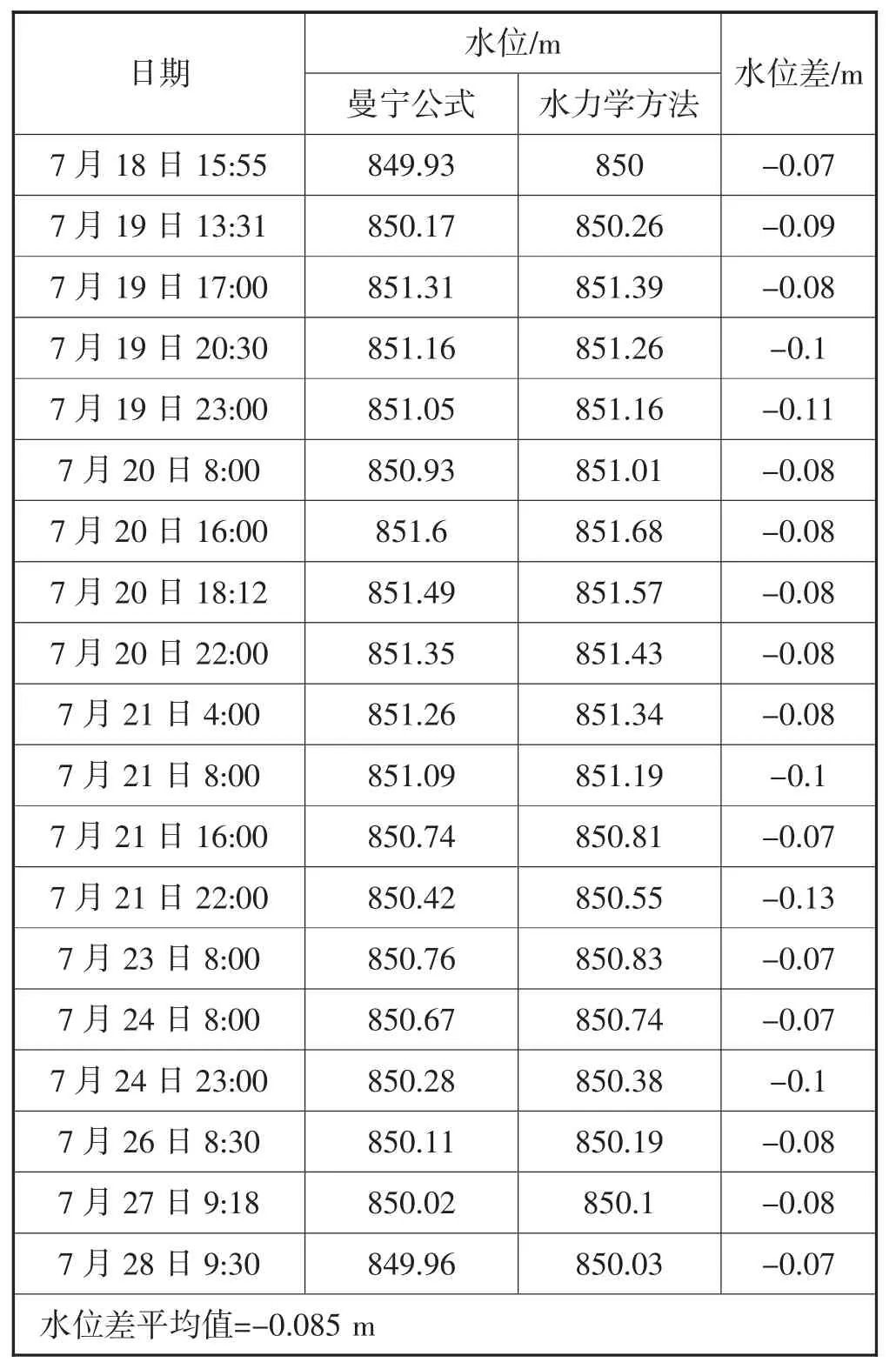
表3 水位值对比分析

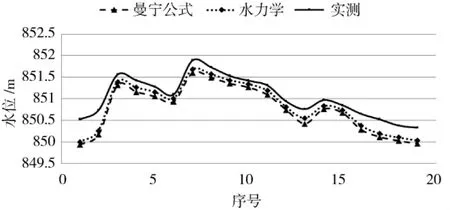
图2 水位对比图

通过表格分析，可以得出曼宁公式与水力学方法计算的断面水位偏低，两种方法计算结果相近，差值为-0.085 m。

3 应用

本文选取两个不同河道进行对比分析，河道位于山西省晋城市高平市野川镇杜寨村以及河底村，属野川河流域，野川河是许河一级支流，流域呈阔叶状，三条支流成扇形交汇，并且均属暴雨型间歇河流，汛期洪水暴涨，枯水季节河道径流枯竭、断流成常年干河。

杜寨小流域面积为25.4 km2，河流长度为3.33 km，河流比降为10.57‰。河底小流域面积为6.5 km2，河流长度为0.91 km，河流比降为28.57‰。

3.1 计算比较

采用《山西省水文计算手册》中的流域模型法计算洪峰流量，然后采用水力学方法和曼宁公式计算出五个不同频率（100年一遇、50年一遇、20年一遇、10年一遇、5年一遇）下的水位值，首、末控制断面能够将沿河村落包进去，起点距为零是河道下游。结果具体见表4。

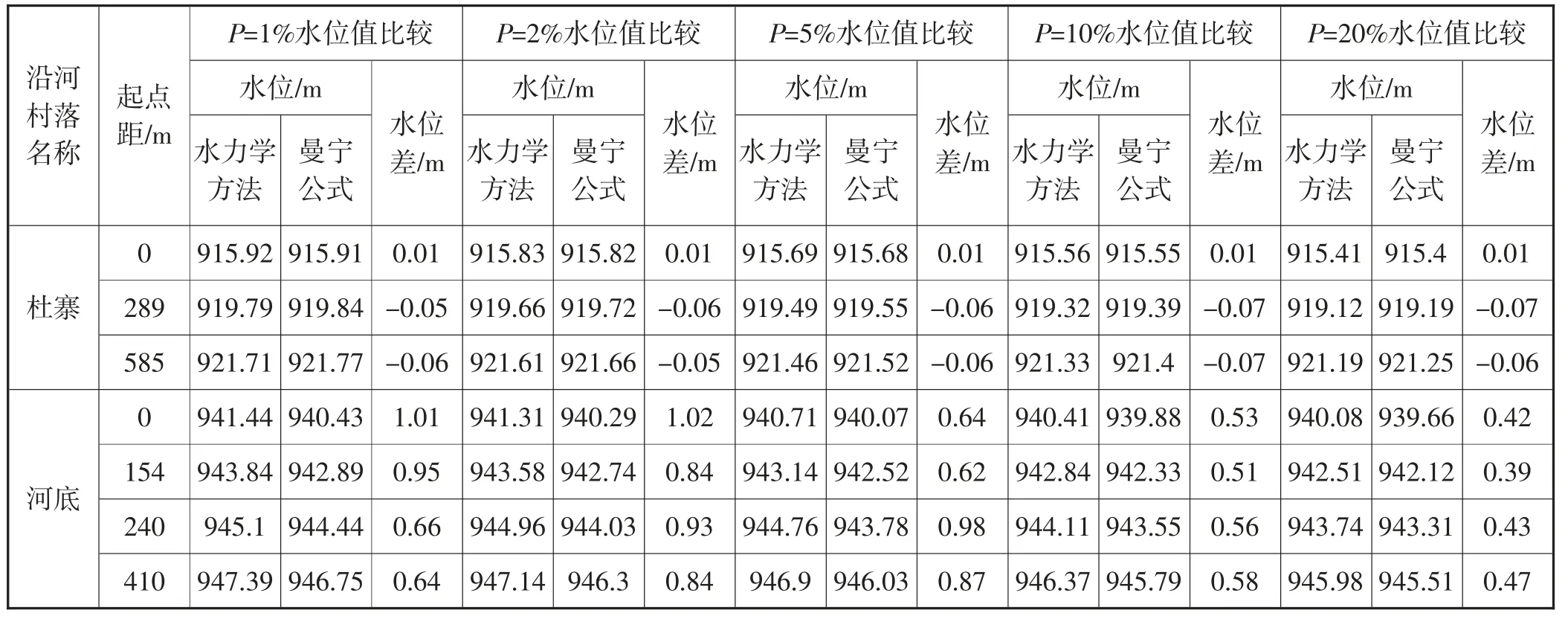
表4 不同频率下水位值比较

4 总结

对比两个河道，河底比降是个关键因素，当河道比降较小的情况下，曼宁公式与水力学方法计算水面线精度相近。随着比降的变大，曼宁公式计算的水位跌落大，与水力学方法计算的水位值相差较大。水力学方法计算水面线时，已知流量值，通过迭代反算可以推出水位值。比降较大的情况下，曼宁公式计算的水位值偏小，水位跌落较大。因此，选取曼宁公式进行水面线计算时，应结合比降进行分析。在比降较小的情况下，两种方法计算结果相近，可以采用曼宁公式进行分析，以简化水面线推求方法。

河道无实测资料，选取适合的水面线推求方法是关键。曼宁公式计算水面线虽然较为简便，但受河道比降影响较大。在采用曼宁公式推求河道水面线时，应该结合比降因素进行分析。