L1-L1/2非负矩阵分解及算法

刘 丹，罗申星

（河北工业大学 理学院，天津 300401）

0 引 言

非负矩阵分解（NMF）[1]是一种有效的降维技术，它将非负矩阵V∈R+m×n近似分解成低秩非负矩阵W∈Rm×r和H∈Rr×n++的乘积，即

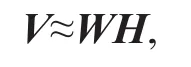
其中r＜＜min{m,n}.NMF具有存储空间小、实现简单等优点，并已成功应用于信号处理[2]、医学[3]、计算机视觉[4]和聚类[5]等.

为了得到矩阵W和H，人们通常用Frobenius范数度量V与WH的距离

其中W≥0和H≥0表示W和H的元素是非负的.

由于稀疏性便于数据的分析以及图像的特征提取，Hoyer等[6]考虑稀疏NMF，在问题（1）中引入L1正则项，提出L1-NMF模型

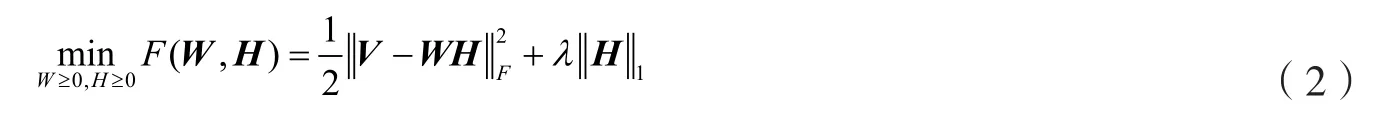
其中λ﹥0，，i=1，2…r，j=1，2…n.因为H≥0，所以.

Xu等[7]发现与L1正则项相比，引入L1/2正则项能得到更稀疏的解.进一步，Cui等[8]在问题（1）中引入L1/2正则项，得到L1/2-NMF模型

为了得到更稀疏的系数矩阵H，本文在模型（1）中引入L1和L1/2正则项，提出L1-L1/2-NMF模型，这样可以同时保留这两个正则项带来的稀疏性效果，即

其中参数λ﹥0，β﹥0.我们提出两种算法求解L1-L1/2-NMF：（1）梯度下降算法；（2）受文献[9]的启发，基于交替非负最小二乘算法框架[10]，提出块坐标下降算法.数值实验中，测试了ORL、CBCL、YALE和Extended-YALE 4个人脸数据集.实验结果表明，与其他稀疏NMF模型相比，求解L1-L1/2-NMF得到的矩阵更稀疏，相对误差更小.

本文将详细介绍求解问题L1-L1/2-NMF的梯度下降算法和块坐标下降算法.同时给出相应的数值实验结果，并对结果进行分析.

1 稀疏非负矩阵分解算法

1.1 梯度下降算法

下面给出GDSNMF算法的推导过程.我们对问题（4）中H的列H:j求导，求导公式为

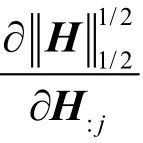
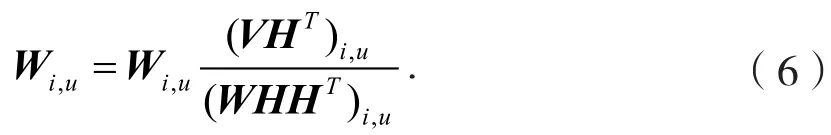
表1给出了GDSNMF算法的详细框架.

表1 GDSNMF算法的详细框架

1.2 块坐标下降算法

基于交替非负最小二乘算法框架，提出一种块坐标下降算法（CDSNMF）求解L1-L1/2-NMF.算法对矩阵W的列和H的行进行分块，实现对矩阵W每一列和H的每一行进行更新.L1-L1/2-NMF的两个子问题可表示为：

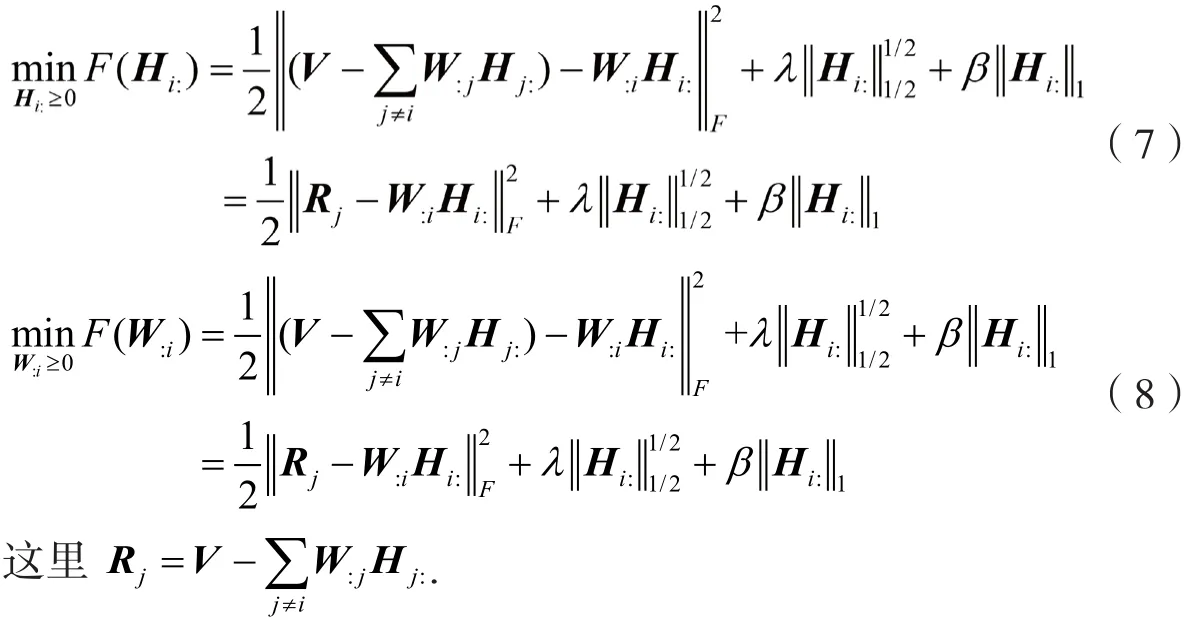
问题（7）的KKT条件为：

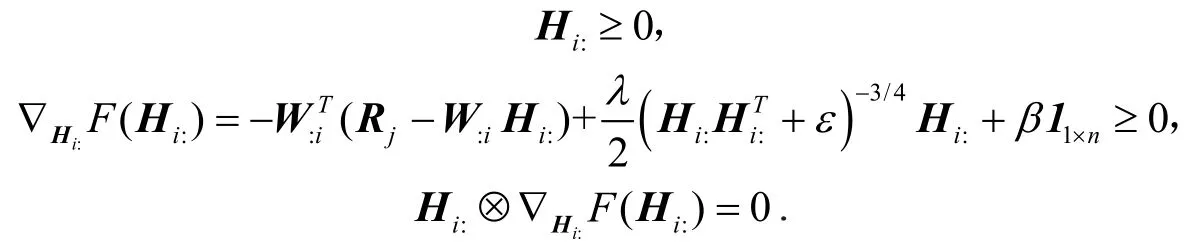
其中符号⊕表示（A⊕B）ij=AijBij.由KKT条件知，问题（7）的极小点满足Hi:F(Hi:)=0，所以H:i的更新规则为

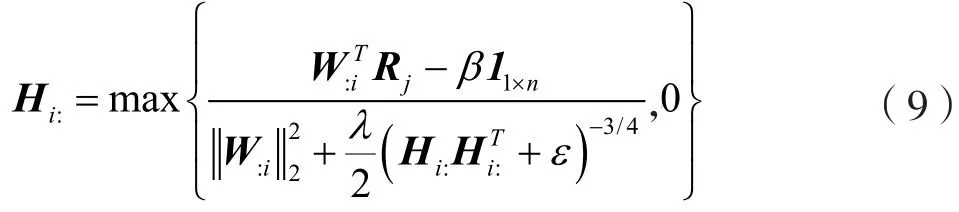
问题（8）的KKT条件为：

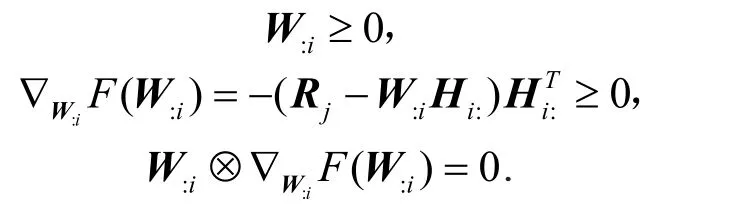
同理，W:i的更新规则为

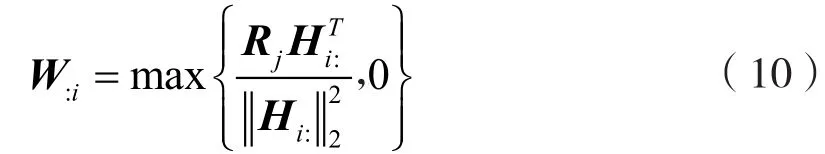
表2给出了CDSNMF算法的详细框架.

表2 CDSNMF算法的详细框架

表3给出了GDSNMF和CDSNMF两种算法的对比.在MATLAB中随机生成一个非负矩阵进行测试.采用文献[11]提出的稀疏度计算公式计算矩阵W和H的稀疏度

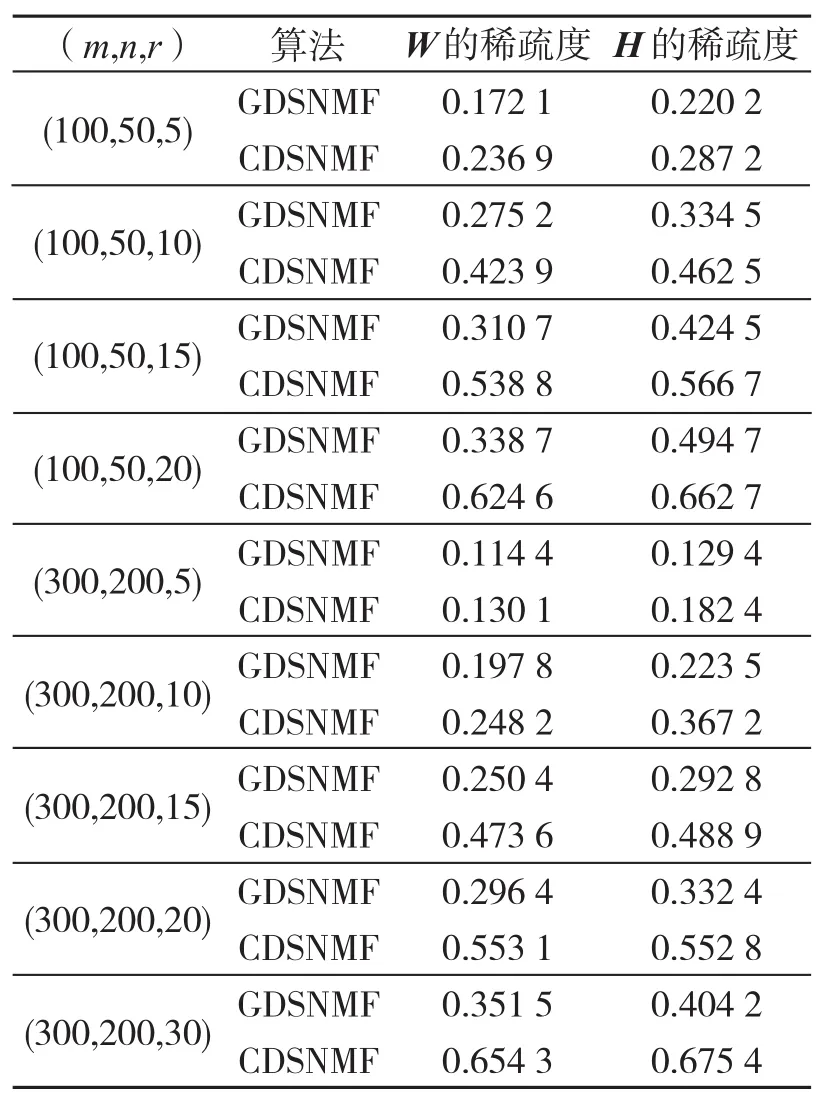
表3 随机生成矩阵的数值实验结果

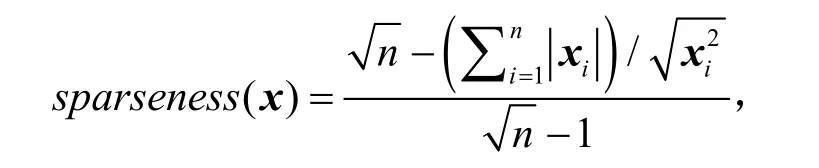
其中n表示向量x的维数.该函数的值域为[0,1]，函数值越小，则向量x越稠密，反之则越稀疏.

从表3中发现当r较小时，两种算法表现相当，但随着r的增大，执行步骤2的次数增多，使得满足KKT条件的W的列数和H的行数增多，CDSNMF算法明显优于GDSNMF算法.

2 数值实验

本节测试稀疏NMF问题，并将GDSNMF和CDSNMF算法与求解L1-NMF的NNSC[6]和求解L1/2-NMF的L1/2-SNMF[8]算法进行比较.数值实验的测试环境为：Windows 10，Core i5-8250U，1.80 GHz，8 GB RAM.

在下列数值实验中，参数选取λ=30，β=5，ε=10-6.

首先，我们考虑文献[9]提到的4个图像数据集ORL、CBCL、Yale和Extended Yale.其中ORL图像数据集包含400张图像，每张图像的像素为32×32，ORL图像数据集表示为一个400×1 024的矩阵.CBCL图像数据集包含2 429张图像且每张图像的像素为19×19，CBCL图像数据集表示为一个2 429×361的矩阵.Yale数据集包含165张图像且每张图像的像素为32×32，Yale图像数据集表示为一个1 024×165的矩阵.Extended-Yale图像数据集包含2 414张图像且每张图像的像素为32×32，Extended-Yale图像数据集表示为一个2 414×1 024的矩阵.公平起见，所有算法采用相同的终止条件，即最大迭代次数达到500次.如表4所示，与NNSC和L1/2-SNMF算法相比，在保证矩阵W稀疏度相差不大的情况下，GDSNMF和CDSNMF算法得到的系数矩阵H更稀疏，且相对误差更小，其中CDSNMF算法的效果尤为明显.

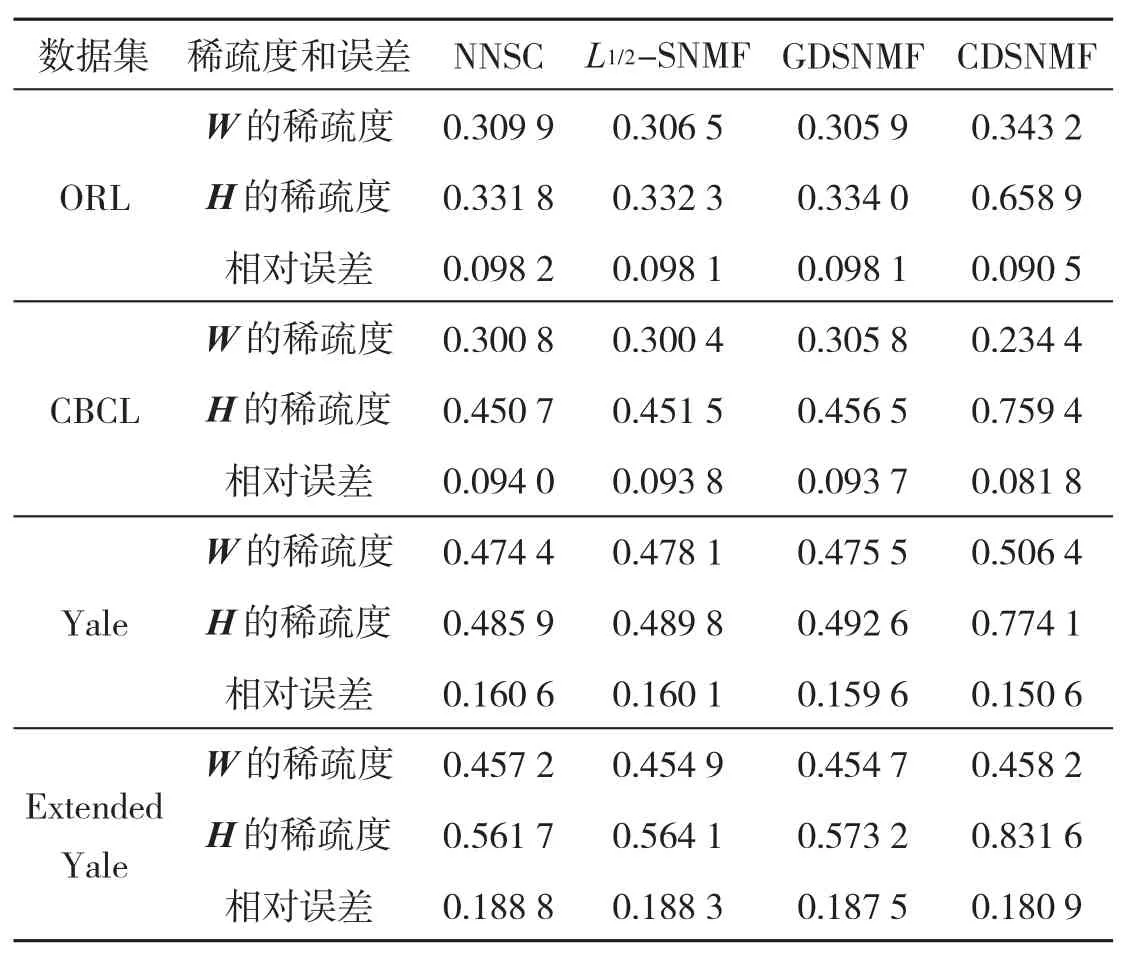
表4 4个数据集的数值实验结果 (r=49)

其次，从ORL图像数据集中随机选取3张人脸图像，且从每张人脸图像中得到一个112×92的矩阵.从表5中可以发现在4种算法得到的重构图效果和矩阵W稀疏度相差不大的情况下，GDSNMF和CDSNMF算法得到的系数矩阵H更稀疏，相对误差更小.

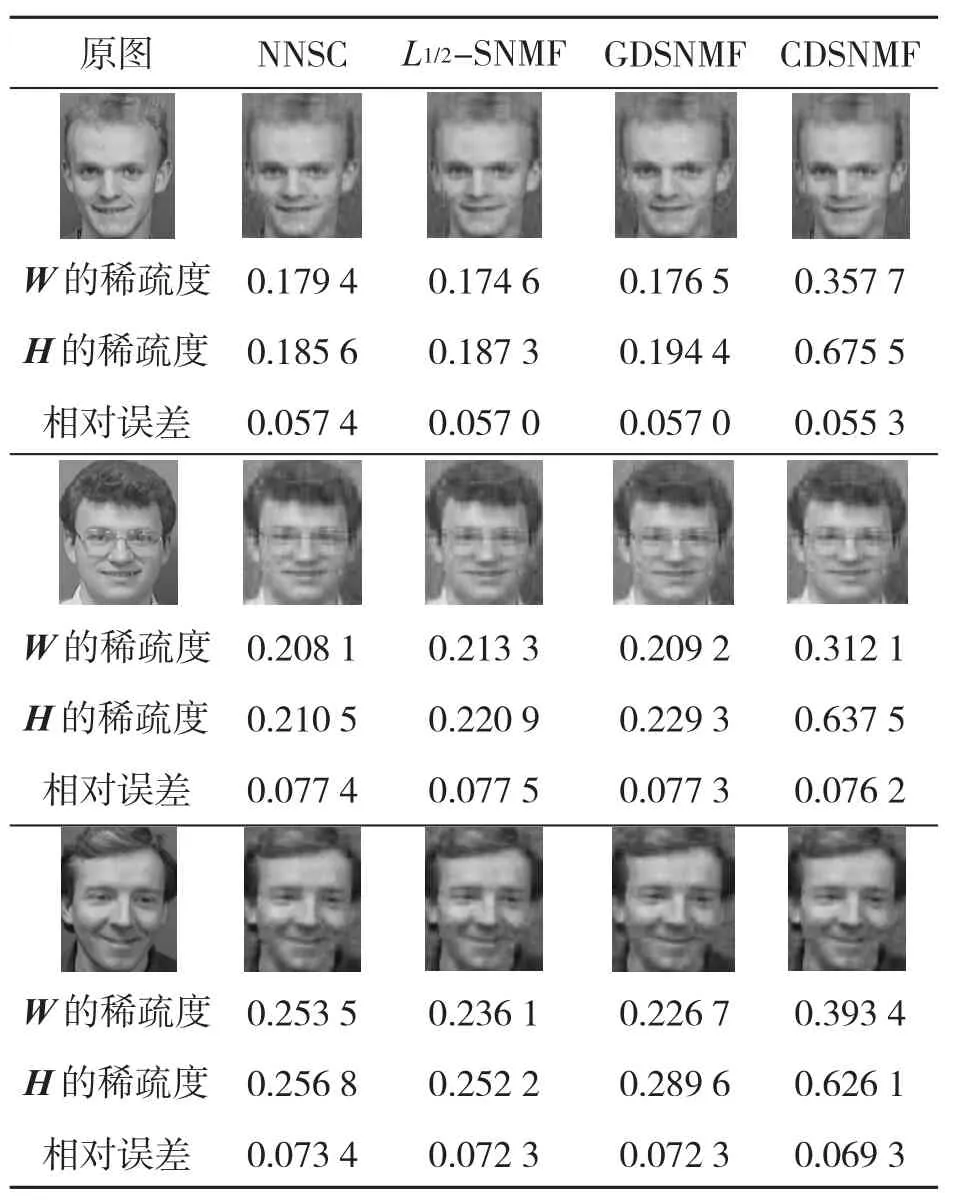
表5 ORL数据集的数值实验结果 (r=10)

3 结论

本文介绍一种新的带L1和L1/2正则项的稀疏NMF模型L1-L1/2-NMF，提出GDSNMF和CDSNMF算法求解该模型.数值实验表明，与求解L1-NMF的NNSC算法和求解L1/2-NMF的L1/2-SNMF算法相比，求解L1-L1/2-NMF的GDSNMF和CDSNMF算法得到的矩阵更稀疏，相对误差更小.