二元函数连续性与沿曲线的连续性之间的关系
2022-03-21常建明
刘 雪,常建明
(常熟理工学院 数学与统计学院,江苏 常熟 215500)
0 引言
根据连续函数的定义,平面区域 Ω 上的二元连续函数z=f(x,y)对自变量x和y分别都是连续的.但反之未必,也就是说,二元函数z=f(x,y)对每个自变量x和y的连续性尚不能保证它是一个连续函数.
例1[1]考察二元函数
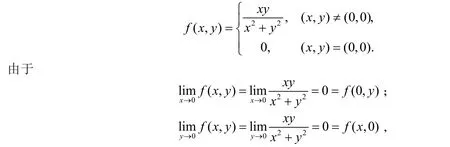
函数f(x,y)在原点(0,0)处关于x和y都是连续的.但是函数f(x,y)在原点处是不连续的:沿直线y=mx(m为任意实数)趋于点(0,0)时,极限
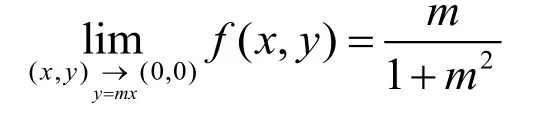
与m有关,从而不存在.
因此当一个多元函数关于各个变量都连续时,如何寻求恰当的条件使得该函数连续的问题就值得去研究.关于此,我们熟知下述结果(见文献1 习题10).
定理1设二元函数z=(fx,y)在 ℜ2上关于自变量x和y都是连续的,并且关于y是单调的,则f是 ℜ2上的连续函数.
我们指出定理1对一般的平面区域Ω也成立.
本文中,我们将推广定理1.我们先对定理1的条件做一些分析.二元函数z=(fx,y)关于自变量x和y的连续性相当于二元函数沿任何直线y=C1和任何直线x=C2的连续性;关于自变量y的单调性相当于二元函数沿任何直线x=C2的单调性.值得注意的是,这两族直线具有如下性质:(1) 每族中任何两条直线都互相平行;(2)每族直线均覆盖了整个平面 ℜ2;(3)不同族中的任两直线互相垂直,从而在区域Q⊂ ℜ2内至多有一个交点.
我们考虑更一般的连续曲线族来代替直线族y=C1和直线族x=C2.如果族中任何两条曲线l1和l2不相交,我们称平面曲线族Г={l}是不自交的.如果区域Ω中的任何点都有族中某条曲线l通过,称平面曲线族Г={l}覆盖了区域Ω.如果Г1中任何一条曲线l1和 Г2中任何一条曲线l2在区域Ω内的交点至多只有一个,我们称两族平面曲线Г1和Г2于区域Ω严格相交.另外,如果对曲线l上任何按序排列的三点P1,P2,P3,f(P2)介于f(P1)和f(P3)之间,我们称函数f沿一条连续曲线l是单调的.
现在,我们的主要结果可叙述如下:
定理2设函数f在平面开区域Ω上有定义,Г1和Г2为严格相交的两族不自交连续可求长平面曲线,都覆盖了区域Ω.如果f沿两族中各曲线均连续,且沿Г2中曲线单调,则函数f在区域Ω上是连续的.
我们指出,很多微分方程的解在平面上就呈现出不自交曲线.因此,定理2具有较好的应用.
1 引理
为证明定理2,我们需要先证明如下辅助引理.
引理 1设Г1和Г2为严格相交的两族不自交连续可求长平面曲线,都覆盖了区域Ω,则对Ω任何内点P0,在Г1和Г2中各有两条曲线,使得这4条曲线围成的区域是Ω的子区域,并且P0是其内点.
证设P0∈Ω 为一内点,则存在δ0>0,使得U(P0,δ0)∩Ω.如图 1 所示,根据条件,曲线族Г1中有曲线l0通过点P0.由于曲线l0为可求长,在l0上存在点A0、B0位于P0的左、右两侧,使得以及如图 2 所示,过点A0、B0分别有曲线族 Г2中曲线m1、m2通过.
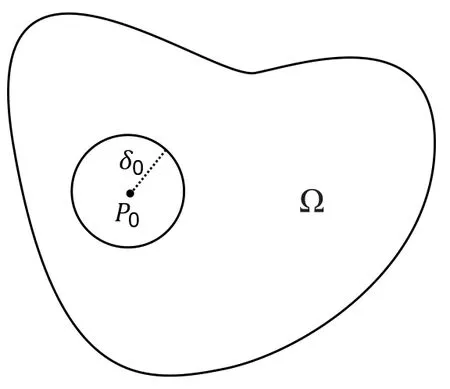
图1 引理1证明参考图1
下证:在m1上存在两点位于l0的两侧,使得通过该两点的曲线族Г1中曲线与m1、m2所围四边形区域含于U(P0,δ0).
先证存在点D0∈m1于l0上侧,使得过D0的曲线l1与l0、m1、m2所围区域含于U(P0,δ0).取点A1∈U(P0,δ0)∩m1(如图2所示).则过点A1有曲线l1∈Г1.
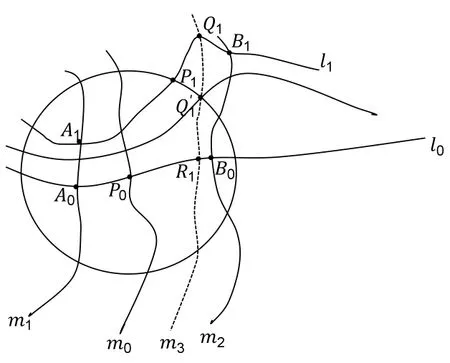
图2 引理1证明参考图2
若l1满足要求,则得证.
若l1不满足要求,设l1与m2交于点B1,则存在点P1∈曲边四边形A0A1B1B0,使得P1∉U(P0,δ0).设四边形A0A1B1B0中上距离最远的点(一定存在,为有界闭集,距离为连续函数)为Q1,过Q1有Г2中曲线m3(可能与m2重合).
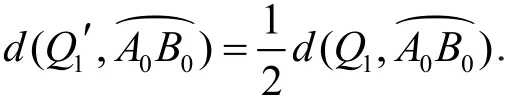
若l2满足要求,则得证.
若l2不满足要求,则同上.因此可定义一列点 {Pn}:Pn∉U(P0,δ0),Pn∈四边形A0A1B1B0.于是有
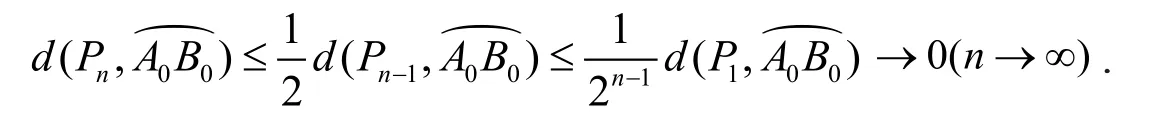
由致密性定理得:Pn有子列收敛于P0*∈A0B0,这与Pn∉U(P0,δ0)矛盾.
所以l0上侧存在四边形A0A1B1B0含于同理l0下侧也存在四边形A0A1B1B0含于U(P0,δ0).于是存在四边形A2A1B1B2含于U(P0,δ0).
引理1证毕.
2 定理2的证明
只要证明f(x,y)在区域Ω上任何一点P0(x0,y0)是连续的.根据引理1,我们可在如图3所示的四边形A2A1B1B2中考虑.由于曲线是可求长的,因此都是可参数化表示的.

图3 定理2证明参考图1
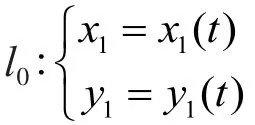

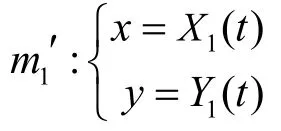
在点M处,按条件函数f(X1(t),Y1(t))在t1处连续,从而存在δ2﹥0 使得当 |t-t1| ≤δ2时有
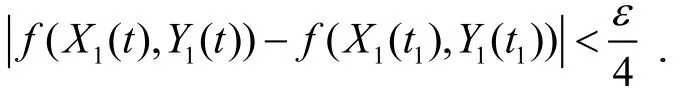
同样点N处,δ3﹥0,使得当 |t-t2| ≤δ3时有
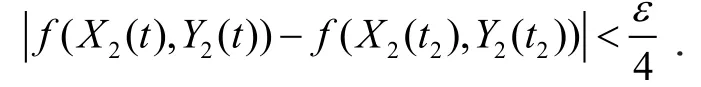
在曲线m1'上取定点D(X1(t1-δ2),Y1(t1-δ2))和C(X1(t1+δ2),Y1(t1+δ2)),在曲线m2'上取定点A(X2(t2-δ3),Y2(t2-δ3))和B(X2(t2+δ3),Y2(t2+δ3)).
设通过点A的Г1中曲线l1'与Г2中曲线m1'交于点D',通过点D的Г1中曲线l2'与Г2中曲线m2'交于点A',按条件,曲线l1'与l2'是不相交的.我们假设靠近(x0,y0)的曲线为l2'.通过点B的Г1中曲线l3'与Г2中曲线m1'交于点C',通过点C的Г1中曲线l4'与Г2中曲线m2交于点B',并且设靠近(x0,y0)的曲线为l3',如图4所示.这样,曲边四边形A'BC'D区域形成点P0(x0,y0)的一个邻域.

图4 定理2证明参考图2
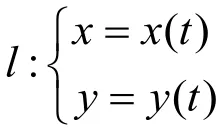
由于f(x,y)沿 Г2中曲线是单调的,因此取δ=min{δ1,δ2,δ3,δ3',δ3'',则当 |t-t0| ≤δ时,有

证毕.
