基于信息融合和堆叠模型的超短期风电功率预测

2022-03-21鲁泓壮丁云飞汪鹏宇

可再生能源 2022年3期

鲁泓壮，丁云飞，汪鹏宇

（上海电机学院电气学院，上海 201306）

0 引言

风电在智能电网体系的比重越来越大[1]。然而，由于风能的间歇性和不稳定性，大规模风电并网对电力系统规划及运行带来了巨大的挑战。为了减轻风电一体化带来的不利影响，有必要从风电功率的超短期预测中获取更准确的信息。这将降低风电备用容量，实现电网及风电场的安全高效运行。

风电功率的超短期预测定义为预测风电场未来15 min～4 h的有功功率[2]。预测方法一般分为物理方法、统计方法和机器学习方法[3]。机器学习方法通过预测模型建立输入输出之间的映射关系，具有良好的数据容错性，适合处理复杂和不确定的关系。具有非线性映射和并行处理能力的统计机器学习模型，如多层感知机（MLP）、支持向量机（SVM）等方法在风电功率预测中得到了广泛应用。

为了达到准确预测，机器学习方法面临的主要问题为风电功率时间序列的非线性、非平稳等特性成为提高模型预测精度的主要障碍；模型的输入特征对预测性能有重要影响。对此，在近几年的研究中，将基于树结构的集成学习作为机器学习中常用的辅助方法，通过综合多种模型的优点建立组合模型以提高预测精度。文献[4]总结了集成方法在风电功率预测中的应用，指出了保证预测结果多样性是集成方法改善预测性能的核心，并将多样性的来源分为数据多样性、模型多样性和参数多样性3类，将集成策略分为基于加权和基于学习器两种。文献[5]通过实验验证了使用不同结构的模型更容易实现“好而不同”的预测结果。文献[6]基于模型多样性构建了堆叠模型，所得到的组合模型优于组合前的模型。文献[7]基于不同核函数的核岭回归构建了堆叠模型，通过多样性的参数实现了基学习器预测结果的差异性，进而提高了融合模型的预测精度。以上文献均未讨论如何通过构建数据多样性来实现预测结果的多样性，而且所用的浅层模型无法自动抽取特征，将会限制预测性能。此外，当使用浅层模型时，适当的特征选择和特征生成方法十分必要[8]。基于此，相关性方法和序列分解方法相继应用到风电功率预测领域[9]。

综合以上，本文提出了一种基于信息融合和堆叠模型的超短期风电功率预测模型。通过对历史测风塔数据和历史功率数据进行序列分解和相关性分析，增强了特征表示和信息利用能力。在堆叠模型的基础上，计及数据多样性构建预测结果的多样性，使用交叉验证和超参数优化以增强预测模型的泛化性能。最后，通过试验验证了所提方法的有效性。

1 基本原理

1.1 模型堆叠方法

集成学习方法通过组合多个独立模型来提高预测精度，其核心在于构造差异化的预测结果，并采取适当的策略结合各个预测结果。

堆叠模型是一种异构的集成学习模型[10]，它利用不同结构的模型来实现预测结果的多样性。为了整合这些模型的决策，可以为每个模型分配不同的权重。一种方法是使用另一个模型来学习整合策略，这种整合方法称为元学习方法。堆叠模型通常具有两层结构，垂直方向包括两种模型，分别称为基学习器和元学习器。第一层中各个基学习器的输出作为第二层元学习器的输入，获得最终结果。

对于基学习器的选择，通常选用神经网络和随机森林这样的强模型（预测偏差小）。从堆叠的思路上看，假设基学习器之间具有不同的“归纳偏好”，通过元学习器整合之后，得到的最终预测结果的方差会降低，从而提升预测精度。

1.2 信息融合方法

信息融合方法是将历史功率序列与历史测风塔数据根据特定标准进行组合，以得到对预测结果的一致性描述[11]。输入数据的多样性是构建预测结果多样性的有效方法，其本质是使用具有不同样本分布的数据集作为预测模型的输入。历史功率时序和气象数据与风功率的映射关系是预测风功率的两个角度，即：

式中：f为所采用的模型；y^为当前功率的预测值；yt-k为之前k个时间间隔的实际功率值；x（i）为与功率相关的风速等的测风塔数据。

将历史功率序列和历史测风塔数据两类数据集分别作为堆叠模型中基学习器的输入，再通过元学习器融合由两类数据集得出的预测结果，其目的是最大限度地利用历史信息以及发挥堆叠模型的优势。

1.3 序列分解与重构技术

将风电功率视为非平稳时间序列，为了提高可预测性，通常采用“分而治之”的序列分解方法。带自适应噪声的完全集成经验模态分解（CEEMDAN）模型是一种将时序分解为本征模态函数（IMF）的方法[12]。CEEMDAN是由EMD和EEMD演变而来，它有效地解决了EMD存在模态混叠和EEMD中噪声残余的问题。但经过分解得到的子序列通常较多，当使用堆叠方法时会增加计算时间。为提高计算效率，同时保证模态间的分辨率，利用样本熵（SE）对相似模式进行重组。SE是一种通过检测信号中产生新模式的概率来衡量时间序列复杂性的指标。对功率序列分解与重构的步骤如图1所示。

图1 功率序列的分解与重构Fig.1 Decomposition and reconstruction of power series

1.4 基于相关性的特征选择方法

1.4.1 偏自相关函数

偏自相关函数（PACF）表达了时间序列和k阶滞后序列之间的纯相关性。对于时间序列yt，滞后k的PACF是指剔除中间k-1个随机变量干扰后，yt-k对yt影响的相关度量。根据上述定义，k阶自回归模型描述如下：

式中：φkk（k=1，2，…）为yt与yt-k在排除中间变量影响后的自相关系数，又称为PACF。

本文利用PACF确定模型输入维数。

1.4.2 斯皮尔曼相关系数

2 模型的结构与方法

2.1 混合预测模型结构

由于风速序列的随机性和复杂性，单个模型的预测性能普遍较差。因此，本文提出了一种结合信息融合的堆叠模型来执行预测任务。图2为所提出的预测方法的整体构造。

图2 基于信息融合和堆叠模型的超短期风电功率预测模型Fig.2 Ultra-short-term wind power forecasting model based on information fusion and stacking

对于功率时间序列，使用CEEMDAN将原始的非平稳功率数据分解为N个IMFs。随后，使用SE计算每个IMF的复杂度，并对类似的IMF进行重新组合，得到q个子序列（q＜N）。采用PACF方法为每个子序列选取适当的滞后步数作为输入特征。本文通过对预测功率及各历史气象数据间进行斯皮尔曼相关性计算，选取高相关性特征作为模型输入。

将处理好的数据集按照3：1的经验比划分成训练集和测试集。针对上述堆叠模型和试验数据的特点，选取MLP、随机森林（RF）、梯度提升回归（GBR）和高斯过程回归（GPR）作为基学习器，SVM作为元学习器。在本研究中使用MLP和RF训练分解重构后的功率序列，叠加后得到当前功率预测值；同时由GBR和GPR训练和预测历史气象数据与当前功率的非线性映射关系。在基学习器上进行K折交叉验证（K=5），以减少过拟合风险，提高预测模型的泛化性能。每个基学习器的预测结果作为元学习器的输入特征集，获得最终结果。

2.2 TPE算法

TPE算法是一种基于采样思想的超参数优化方法[13]，与网格搜索和随机搜索相比，TPE算法以较小的代价获得更好的结果。TPE算法通过贝叶斯定理获取代理模型的后验分布，进而获得模型性能与超参数之间的关系。通过下式将p（x|y）变成两个概率密度函数：

令γ=p（y＜y*），通过正比项可以看出，EI倾向于选取l（x）较大和g（x）较小。通过此种方法对开发和探索进行权衡，寻找全局最优超参数。

2.3 模型评价指标

为了评估模型的预测性能，本文采用均方根误差（RMSE）和平均绝对百分比误差（MAPE）作为预测性能评估标准。

式中：n为样本数量；yi为测量值；y^i为预测值。

3 算例分析

3.1 数据收集与处理

通过东北地区某装机容量为14 MW的风电场对所提出的模型进行验证。选取该风电场2017年10月1日-21日共2 000组数据作为数据集，时间间隔为15 min。对原始数据集进行数据预处理，采用时空临近法处理缺失值，根据风向对原始风速序列进行矢量分解[14]。取前1 500组作为训练集，后500组作为测试集。

CEEMDAN将原始功率序列分解为8个IMF分量和1个残差分量[图3（a）]。为了减少计算量，避免过度分解，采用SE技术对上述分解模式进行分析。将SE值相近的模式组合成新的子序列，相似度容差设为0.2个标准差，重构维数为2。根据样本熵值对CEEMDAN各模态分类，结果如图3（b）所示，最终得到5个新的子序列如图3（c）所示。

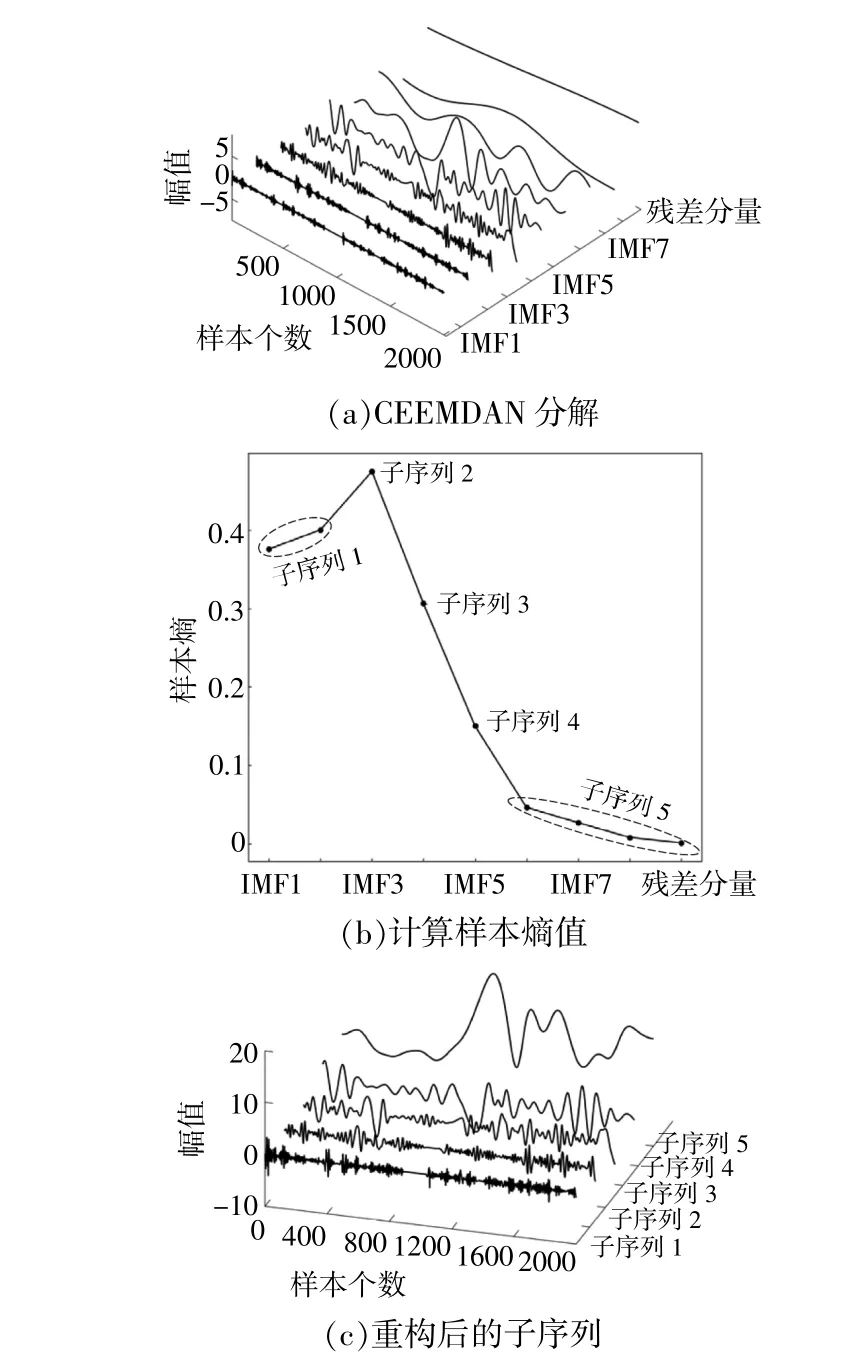
图3 风电功率序列分解与重构过程Fig.3 Wind power series decomposition and reconstruction process

3.2 特征选取

为了获得最佳变量作为预测模型的输入，PACF方法用于提取与每个子序列具有较高相关性的滞后序列。在yt作为输出变量，且滞后k（设k≤9）处的PACF超出90%置信区间的情况下，将yt-k用作输入变量。表1为通过PACF方法选取的各子序列的输入组合。

表1 基于PACF的特征提取结果Table 1 Feature extraction results based on PACF

充分利用历史信息建立精确的回归预测模型，同时考虑风速等与功率值相关的历史气象数据。设置斯皮尔曼相关系数的阈值为0.5，选取相关性较高的历史气象特征作为输入特征。图4为当前功率值与输入特征之间的相关性分析。

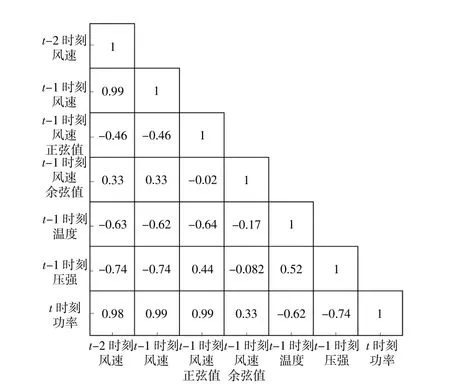
图4 当前功率与测风塔输入特征的斯皮尔曼相关性分析结果Fig.4 Spearman correlation analysis results of current wind power and wind tower input characteristics

3.3 参数优化

对于各个模型中的关键超参数，使用Hyperopt中包含的TPE算法进行调优[15]。为了防止模型在训练过程中出现过拟合，本文采用5折交叉验证。采用均方根误差作为模型选择的目标函数。也就是说，在每个优化试验中，通过交叉验证选取预测误差最小的超参数配置。为了实现损失函数收敛，将迭代次数设置为100。

3.4 预测结果与对比分析

为验证所提出模型的预测性能，选用长短期记忆网络（LSTM）、轻量级梯度提升机（LightGBM）和本文所用基学习器CEEMDAN-SE-RF与之进行对比分析。其中，LSTM使用前8个时间段的功率和气象特征作为模型输入；LightGBM通过斯皮尔曼相关分析选取历史特征，方法与文献[16]类似；RF使用本文设计的模态分解重构方法。各模型在测试集上的预测结果如图5所示。

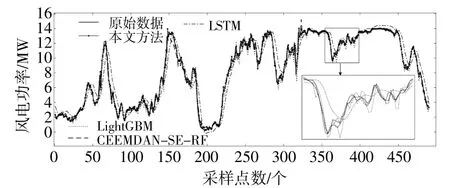
图5 测试集预测结果对比Fig.5 Forecasting result comparison of test set

不同预测模型的预测误差绝对值的箱型图如图6所示，与其他模型相比，本文方法具有较小的变化范围和较小的异常值。

图6 预测误差绝对值的箱型图Fig.6 Box-diagram of forecasting error absolute value

对各模型预测结果进行误差分析，结果如表2所示。

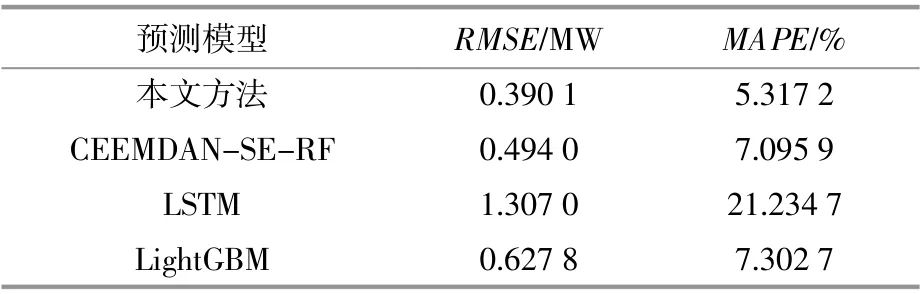
表2 各模型预测误差比较Table 2 Comparison of prediction errors among differentmodels

由表2可知：LSTM的误差明显高于其他模型，这是因为LSTM并未对输入特征进行选择，使得冗余的输入特征降低了模型的学习能力；CEEMDAN-SE-RF相对于LightGBM的误差较小，这是因为CEEMDAN-SE-RF所应用的模态分解与重构技术可以改善原始风电功率序列的非平稳性，进一步提高了预测性能；相比于CEEMDAN-SE-RF，本文方法的RMSE和MAPE分别降低了0.103 9 MW和1.778 7%，验证了堆叠模型的有效性。本文方法和LightGBM均考虑到外生变量所造成的影响，而构造了数据多样性的本文方法的误差明显小于LightGBM。