永磁同步电机参数扰动抑制方法

张硕，李雪荣，崔星，汪洋，张承宁

（1. 北京理工大学 机械与车辆学院，北京 100081；2. 中国北方车辆研究所，北京 100072）

永磁同步电机(permanent magnet synchronous motor，PMSM)因其高效率和高功率密度等优点被广泛应用于新能源汽车领域[1-2]. PMSM控制系统中常用的控制策略包括比例积分(proportional integral, PI)控制和无差拍电流预测控制(deadbeat predictive current control，DPCC). PI控制器中PI参数的选择一般需要根据实验经验，在电机参数发生变化时需要重新设计PI参数[3]. DPCC根据预测模型对电机未来的状态进行预测，具有开关频率固定、电流谐波小和动态响应快的优点，是一种具有前景的控制算法[4]. 预测模型一般为电机的数学模型，包含定子电阻、定子电感和转子磁链等参数，这些参数会受到运行温度、定子电流以及磁通饱和等不可控因素的影响，所以预测控制性能的好坏取决于模型是否准确[5].

参数辨识法是将辨识出的参数值代替发生扰动的参数值，包括最小二乘法、扩展卡尔曼滤波法、模型参考自适应法等[6-8]. 但是参数辨识法一般比较复杂，对处理器运算性能要求比较高. 扰动观测器法通过补偿参数扰动带来的影响间接解决参数扰动. 刘京等[9]采用了滑膜观测器观测参数扰动，并将扰动量前馈进行补偿. 但在滑膜控制系统中，趋近速度和抖振是一对矛盾. YAN等[10-11]采用了龙伯格观测器进行参数扰动的观测，但是龙伯格观测器要求线性的被控对象模型，而且对系统已知信息要求比较多.殷婷婷等[12]采用了扩张状态观测器，但是扩张状态观测器结构比较复杂，涉及到参数也比较多，不但增加了控制系统的延时，而且增加了控制系统的复杂程度.

针对采用id= 0控制的表贴式PMSM控制系统，为提高控制系统的参数鲁棒性，文中提出了一种利用自回归模型估计定子电感和定子电阻扰动的方法，该方法理论简单且容易实现，仿真和实验结果验证了所提方法可以有效抑制电阻和电感扰动.

1 参数扰动影响

首先介绍表贴式永磁同步电机的数学模型，然后根据永磁同步电机的数学模型建立预测模型分析参数扰动带来的影响.

1.1 表贴式永磁同步电机数学模型

研究选择三相表贴式永磁同步电机作为研究对象，理想条件下d-q旋转坐标系下的电机数学模型表达式为

式中：id、iq分别为d、q轴定子电流；Ud、Uq分别为d、q轴定子电压；Rs、Ls、Ψf分别为定子电阻、定子电感和转子磁链；ωe为电机的电气角速度.

1.2 无差拍电流预测控制

无差拍电流预测控制通过预测模型实现对永磁同步电机的预测控制，结合了调制策略，能够获得使代价函数为零的最优电压矢量，具有良好的动、静态特性.

将表贴式永磁同步电机的电压方程进行一阶欧拉向前离散化获得预测模型. 假设当前时刻为k，离散后的永磁同步电机电压方程可表示为

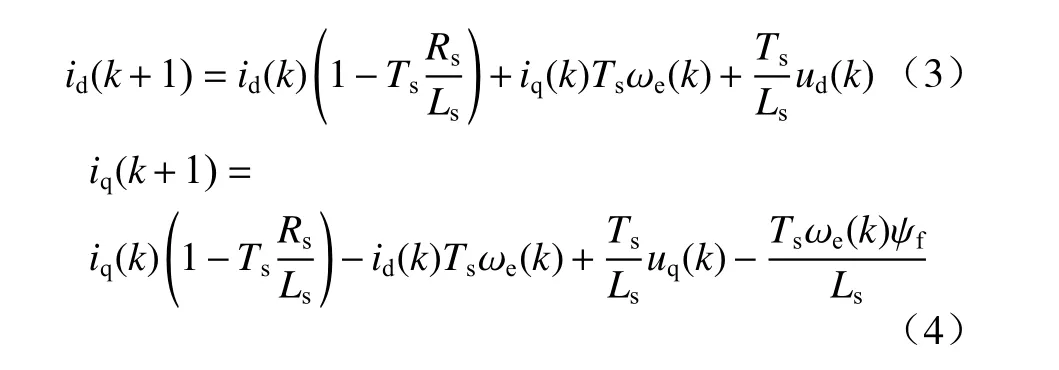
式中：ud(k)、uq(k)为k时刻作用于永磁同步电机的d、q轴电压；id(k)、iq(k)为k时刻永磁同步电机d、q轴实际电流，id(k+1)、iq(k+1) 为k+ 1时刻永磁同步电机d、q轴预测电流；Ts为一个控制周期.

根据控制目标选择代价函数. 本研究选择定子电流作为控制目标，为保证预测电流能够跟踪参考电流，代价函数可以表示为

令代价函数J等于零获得作用于表贴式永磁同步电机的最优电压矢量.

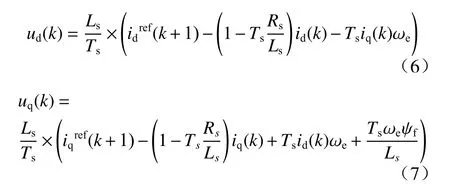
1.3 参数扰动

永磁同步电机的参数扰动会导致预测模型不准确，影响无差拍电流预测控制的性能. 其中定子电阻，定子电感等电机参数会受到运行温度、磁场饱和等因素的影响发生变化.

考虑表贴式永磁同步电机的参数发生了扰动，实际的电机参数不再等于电机的铭牌值. 将无差拍电流预测控制中的预测模型改写为实际电机参数.

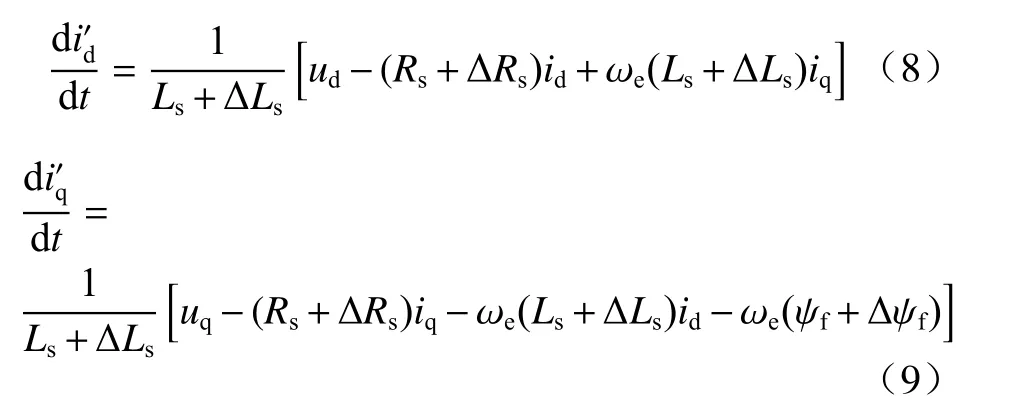
式中：ΔLs为定子电感扰动量；ΔRs为定子电阻扰动量；ΔΨf为转子磁链扰动量.

比较发生扰动的预测模型与理想的预测模型可以得到参数扰动带来的预测误差.

由式(10)和式(11)可以看出，永磁同步电机的参数扰动会带来预测电流误差，最终导致预测控制算法的失效.

2 参数扰动抑制

根据无差拍电流预测控制原理，无差拍电流预测控制中的预测模型依赖准确的电机参数，如定子电阻、定子电感和转子磁链. 在实际运行过程中，永磁同步电机的参数会随着运行条件和运行环境的变化而发生变化，比如，电机的绕组电阻和电感会随着温度的变化而变化. 当电机的参数发生变化时，预测模型失真，无差拍电流预测控制的性能会被破坏.

为了抑制定子电阻和定子电感的扰动，本研究选择自回归模型估计电阻和电感扰动并进行补偿，然后结合无差拍电流预测控制策略实现对永磁同步电机的控制.

2.1 自回归模型定义

自回归模型[13]利用自身做回归变量，利用前若干控制周期的随机变量的线性组合来描述以后某个控制周期的随机变量. 因为前若干控制周期内的随机变量包含了对当前控制周期随机变量有用的信息.对前若干控制周期随机变量进行提取，即可获得当前控制周期的随机变量.

如果假设一个时间序列为x1、x2、x3……xn，并且是p阶自回归模型. 那么时间序列中xt可以表示为前p个序列的线性组合及误差项et的函数，一般形式的数学模型可以表示为

式中：a0为常数项，a1，a2，……，ap为自回归模型参数，et为具备均值为0，方差为σ的白噪声.

当a0=0时，称为中心化自回归模型. 为了简便起见，本研究选择了中心化自回归模型.

2.2 自回归模型+无差拍电流预测控制

本研究选择自回归模型估计参数扰动并前馈进行补偿. 将式(1)和式(2)改写为

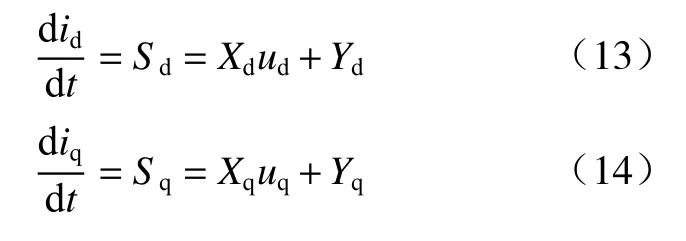
式中：Xd和Xq为电压系数；Yd和Yq为待估计的未知参数.

改写后的预测模型中不包含定子电阻，定子电感等信息，它们用Xd、Xq、Yd和Yq代替. 因此，只要估计出Xd、Xq、Yd和Yq，就可以完成预测模型的构建.考虑到控制周期足够短，相邻控制周期内Xd、Xq、Yd和Yq的变化可以忽略不计，Xd、Xq、Yd和Yq可以表示为

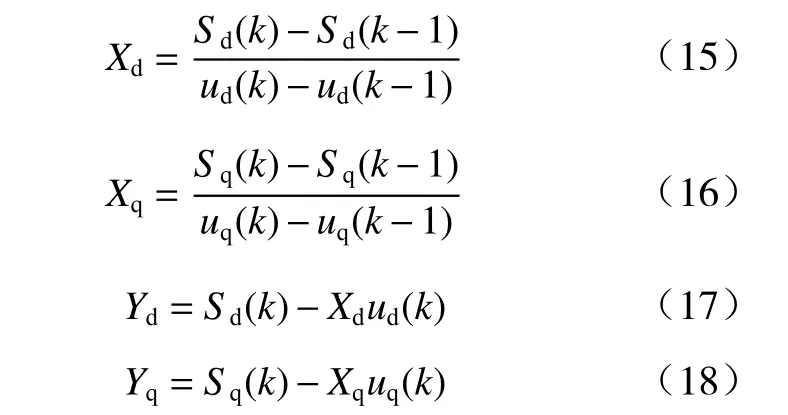
本研究将考虑定子电阻和定子电感扰动的预测模型设计为

本研究将参数扰动Ed和Eq设计为2阶中心化自回归模型，并表示为

式中：Ed(k-2)和Eq(k-2)为k-2时刻参数扰动带来的斜率预测误差；Ed(k-1)和Eq(k-1)为k-1时刻参数扰动带来的斜率预测误差；Ed(k)和Eq(k)为待估计的k时刻参数扰动带来的斜率预测误差；λ为待调节的系数.

将自回归模型代入到预测模型中，可以得到考虑参数扰动的无差拍电流预测控制公式.

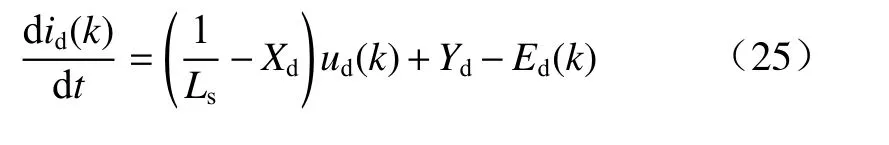
同样令代价函数等于0求出作用于永磁同步电机的最优的电压矢量.本研究提出的参数扰动抑制方法的原理框图可以表示为如图1所示.

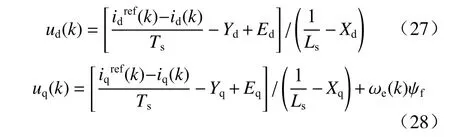
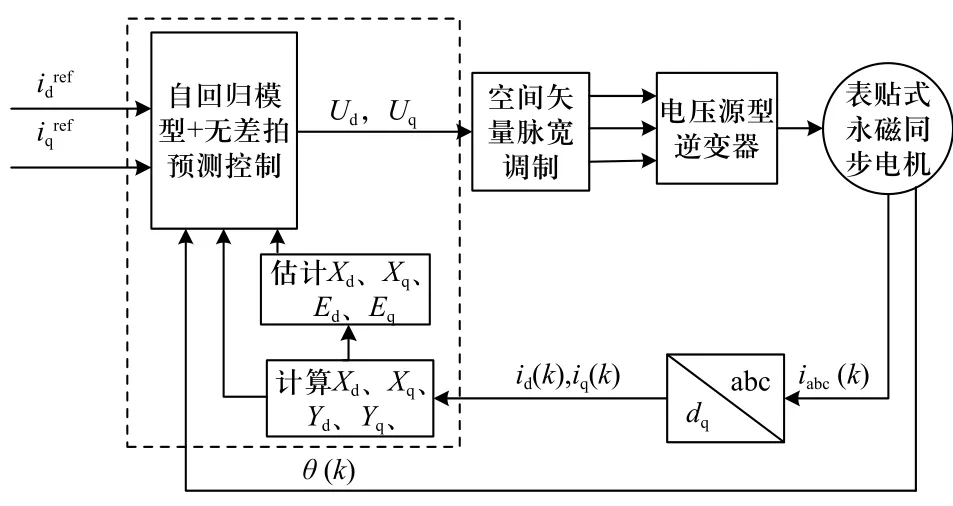
图1 参数扰动抑制方法原理框图Fig. 1 The block diagram of the parameter disturbance suppression method

3 仿真和实验结果分析

为了验证本研究提出的参数扰动抑制方法可以有效抑制定子电阻和定子电感扰动，在Matlab/Simulink仿真环境下搭建仿真模型进行仿真验证并在实验台架上进行实验验证. 本研究通过改变无差拍电流预测控制算法中的电机参数来模拟实际电机内部参数发生扰动完成失配实验.

3.1 研究对象

根据实验台架上使用的永磁同步电机型号，在仿真环境下搭建了相同电机参数的电机模型. 台架实验中使用的三相表贴式永磁同步电机(SPMSM)具体参数信息如表1所示. 表1中：p为电机的极对数；Rs为定子电阻；Ls为定子电感；Ψf为转子磁链；J为转矩惯量；PN为额定功率；TN为额定转矩.

表1 三相表贴式永磁同步电机参数Tab. 1 The parameters of three-phase surface-mounted PMSM

3.2 实验平台

实验采用的表贴式永磁同步电机实验平台如图2所示，主要包括驱动电机、负载电机、示波器、转矩分析仪、30 V高压电源、12 V低压电源、仿真器、计算机、控制板、驱动板和旋变解析板. 其中控制板上的控制器芯片为DSP-TMS320F28377d.

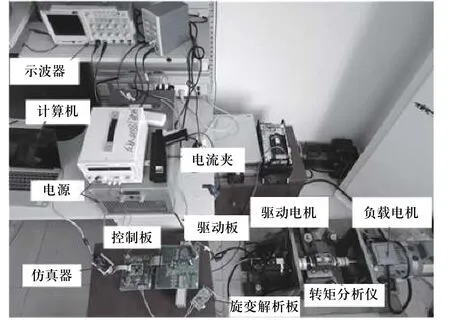
图2 永磁同步电机驱动系统实验平台Fig. 2 The experimental platform of the PMSM drive system

3.3 结果分析

本研究分别在不同工况下进行了仿真验证和实验验证. 其中λ设置为0.9，a1设置为0.01，a2设置为0.09，开关频率为20 kHz.

3.3.1 仿真结果分析

图3和图4是电感扰动量的仿真实验结果，电感仿真实验工况设置为转速800 r/min，负载转矩从2 N·m阶跃到7 N·m，随后降到3 N·m. 为了验证所提出的扰动抑制方法的有效性，在相同的工况下对无差拍电流预测控制方法也进行了仿真实验. 将无差拍电流预测控制方法称为方法1，提出的参数扰动抑制方法称为方法2.

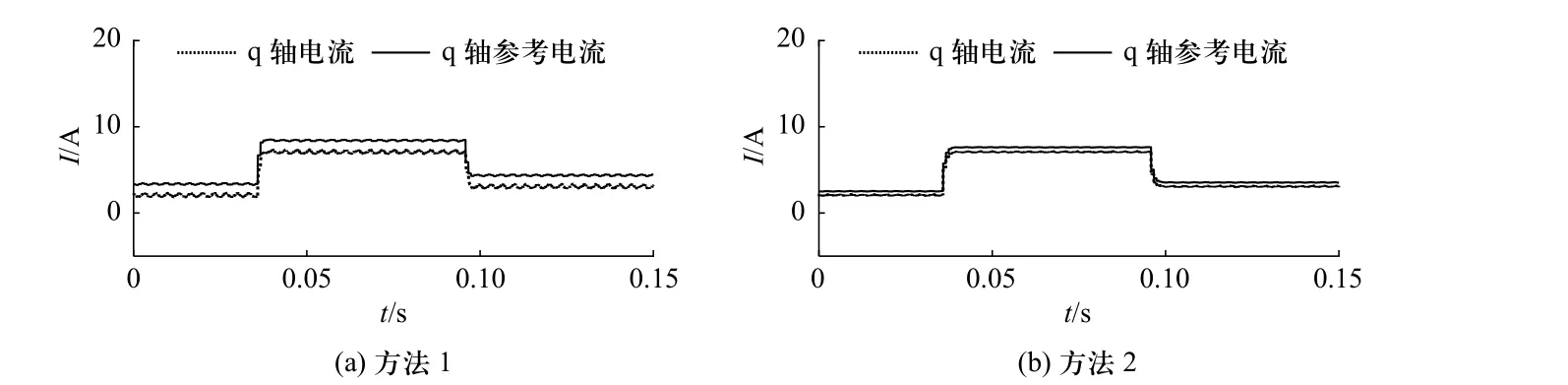
图3 电感0.3倍失配仿真结果Fig. 3 Simulation result under inductance mismatch (0.3 times)

图4 电感2倍失配仿真结果Fig. 4 Simulation result under inductance mismatch (2 times)

图3和图4的仿真结果表明本研究提出的参数扰动抑制方法提高了传统无差拍电流预测控制方法对电机定子电感的鲁棒性，在电感出现负向扰动时，方法2的q轴电流可以更准确地跟随q轴参考电流，在电感出现正向扰动时，方法2可以降低q轴的电流波动.

为了验证提出的参数扰动抑制方法对电阻同样具有鲁棒性，设置了图5和图6所示的电阻扰动量的仿真实验. 电阻仿真实验工况设置为转速900 r/min，负载转矩从3 N·m阶跃到6 N·m，随后降到4 N·m. 同样，将无差拍电流预测控制方法称为方法1，提出的参数扰动抑制方法称为方法2.

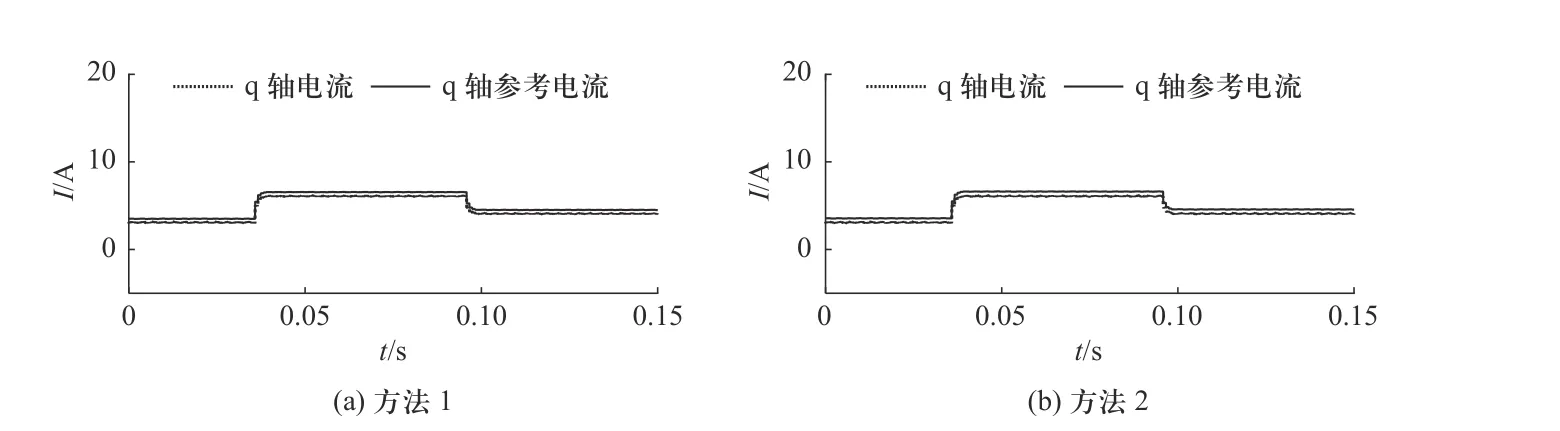
图5 电阻0.1倍失配仿真结果Fig. 5 Simulation result under resistance mismatch (0.1 times)

图6 电阻15倍失配仿真结果Fig. 6 Simulation result under resistance mismatch (15 times)

图5和图6的仿真结果表明，本研究提出的参数扰动抑制方法提高了传统无差拍预测控制对电机定子电阻的鲁棒性，当电阻出现正向扰动时，方法2的q轴电流可以更准确地跟随q轴参考电流，当电阻出现负向扰动时，方法2的电流特性可以达到跟方法1同样的效果.

根据上述的曲线图可知，在电感出现负向扰动时，方法2的q轴电流跟随百分比比方法1高，在电感出现正向扰动时，方法2的q轴电流纹波比方法1小；在电阻出现负向扰动时，方法2的电流跟随百分比可以达到跟方法1近似的数值，但是当电阻出现正向扰动时，方法2的q电流跟随百分比要高于方法1.

3.3.2 实验结果分析

进一步在实验平台上对提出的参数扰动抑制方法进行了实验验证.

图7为电感0.5倍失配，转速800 r/min，负载转矩从3 N·m阶跃到7 N·m，再降落至2 N·m的台架实验结果. 图8为电感3倍失配，转速800 r/min，负载转矩从2 N·m阶跃到8 N·m，再降落至5 N·m的台架实验结果.

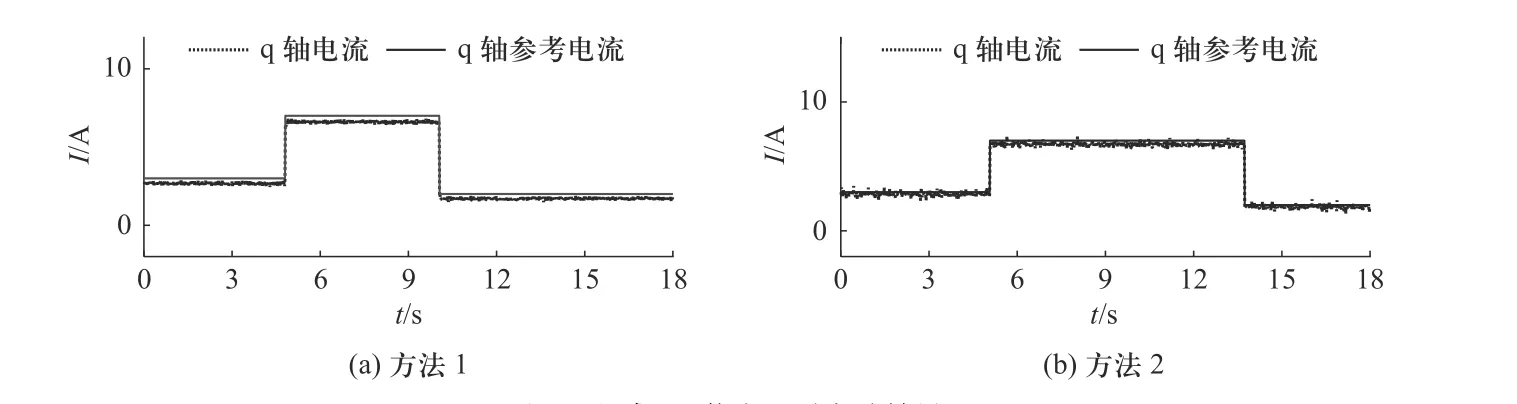
图7 电感0.5倍失配时实验结果Fig. 7 Experimental result under inductance mismatch (0.5 times)

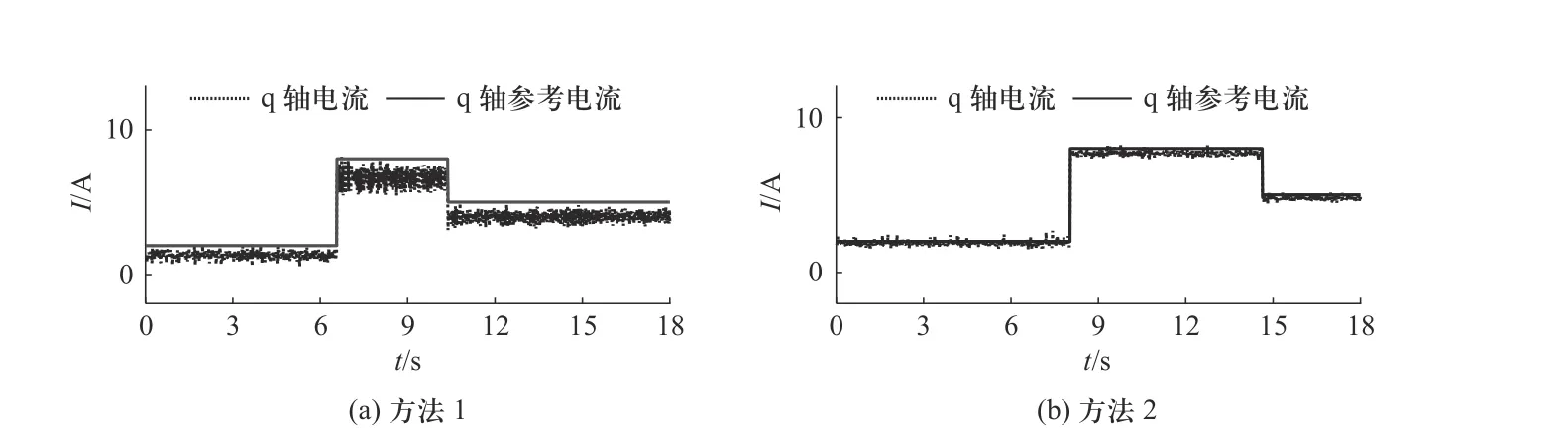
图8 电感3倍失配时实验结果Fig. 8 Experimental result under inductance mismatch (3 times)

图7和图8的实验结果表明本研究提出的参数扰动抑制方法可以有效抑制电感扰动，在电感出现负向扰动量时方法2的q轴电流能够准确跟随q轴参考电流，在电感出现正向扰动量时，方法2可以降低电流谐波含量.

在电阻出现扰动时也进行了台架实验验证. 图9为电阻15倍失配，转速800 r/min，负载转矩从3 N·m阶跃到6 N·m再降到4 N·m的台架实验结果. 图10为电阻0.1倍失配，转速800 r/min，负载转矩从3 N·m阶跃到6 N·m再降到4 N·m的台架实验结果.

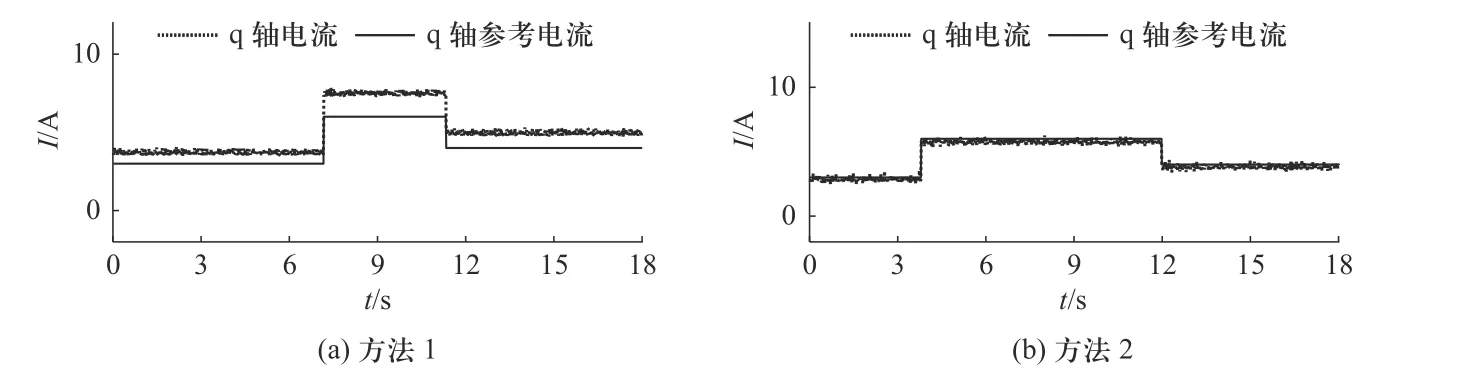
图9 电阻15倍失配时实验结果Fig. 9 Experimental result under resistance mismatch (15 times)

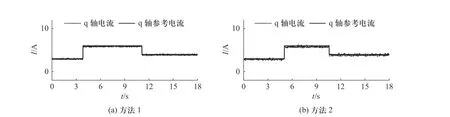
图10 电阻0.1倍失配时实验结果Fig. 10 Experimental result under resistance mismatch (0.1 times)

从图9和图10的实验结果中可以看出提出的参数扰动抑制方法也可以抑制电阻的扰动，使反馈的电流可以准确跟随参考电流.

为了实验结果的充分性，在电阻和电感同时失配时也进行了台架实验验证. 图11是电阻0.1倍失配，电感0.5倍失配时的实验结果，负载转矩设置为从3 N·m阶跃至7 N·m，再降落至5 N·m. 图12是电阻15倍失配，电感2倍失配时的实验结果，负载转矩设置为从2 N·m阶跃至7 N·m，再降落至3 N·m. 转 速都是800 r/min.

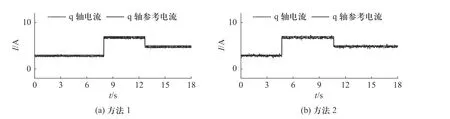
图11 电阻0.1倍失配电感0.5倍失配时实验结果Fig. 11 Experimental result under inductance (0.5 times) and resistance (0.1 times)mismatch

图12 电阻15倍失配电感2倍失配时实验结果Fig. 12 Experimental result under inductance (2 times) and resistance (15 times)mismatch

从实验结果中可以看出，在电阻和电感同时发生扰动时，方法2中的电机q轴实际电流依然能够准确跟随q轴参考电流，抑制了电阻和电感的扰动，证明了提出的参数扰的抑制方法可以有效抑制电感和电阻的扰动.

4 结 论

本研究针对无差拍电流预测控制提出了一种参数扰动抑制方法，该方法利用自回归模型估计定子电阻和定子电感扰动，结合无差拍电流预测控制实现对三相表贴式永磁同步电机的控制. 仿真和实验结果证明了提出的参数扰动抑制方法可以有效抑制电阻和电感的扰动. 文中提出的参数扰动抑制方法简单可靠，算法成本低，能够实现一定容差率的参数扰动. 并且在实际应用中，对应用环境的参数配置要求较低，实际运用时鲁棒性好，符合实际应用的需求. 特别是在对控制精度要求不苛刻的场合，对于实际电机控制具有很强的现实指导意义.