基于低秩矩阵近似的鲁棒DOA估计方法

温超，徐丽云，段鹏婷

（1. 山西大学 大数据科学与产业研究院，山西，太原 030006；2. 北方自动控制技术研究所，山西，太原 030006）

传感器阵列波达方向(direction of arrival, DOA)估计在雷达、声纳、导航、无线通信和语音信号的处理应用中发挥着重要作用[1-3]. 该技术利用阵列输出数据或者其相关矩阵包含的入射信号方向及能量分布信息, 解决同时到达信号的方向估计问题[4]. 传统估计方法显式或者隐式地假定传感器噪声是等方差的空间不相关的高斯白噪声, 噪声协方差矩阵是对角阵. 在这种情况下, 常规最大似然(maximum likelihood, ML)方法[5-6]可预期得到好的估计结果. 若存在非均匀传感器响应、非理想接收通道以及非均匀介质[7]等情况, 则噪声在空间上是白色的但其方差并不相同, 即噪声协方差对角阵元素各不相同. 这种噪声模型同样适用于声纳混响噪声或外部地震噪声[7-8]. 值得注意的是, 这种情况下基于均匀白色噪声或一般彩色噪声假设[9-10]的DOA估计方法可能无法给出令人满意的结果, 因为前者盲目均等地对待所有传感器响应而后者忽略了传感器外部噪声的相关性[7-11]. 因此, 如何提高在这种非均匀噪声环境中的DOA参数估计性能是当前阵列信号处理领域的研究热点之一.

近似最大似然(approximate maximum likelihood,AML和常规最大似然一样)估计方法[12]利用无信号(仅噪声)样本中估算噪声协方差矩阵, 通过白化接收数据和估计信号子空间获得DOA估计, 但实际中难以获得无信号样本, 限制了该方法的广泛应用. 基于非均匀噪声的ML方法[7,13-15]可以获得比基于均匀噪声的ML方法更好的估计精度, 其通过关于信号和噪声参数的目标函数的分步集中来得到DOA的估计. 虽然这些ML方法实现了较高的估计精度,但大多数需要耗时的多维搜索, 并且性能依赖于高信噪比和大量快拍, 极大限制了其广泛应用. 为此,基于稀疏重构的参数估计方法[16-18]近年来相继被提出, 其利用信号空域稀疏特性, 通过参数离散化去除观测模型中的方向变量, 将DOA估计问题转化为线性模型下的稀疏信号恢复问题, 有利于提高在低信噪比条件下估计性能的鲁棒性. BHASKAR等[19]提出基于原子范数最小化的噪声抑制方法, 并利用阵列输出的一阶统计量模型和噪声统计量先验知识获得较好的参数估计性能. YANG等[20]进一步利用原子范数最小化方法解决压缩数据条件下正弦信号的频率估计问题, 并分析了压缩数据对频谱估计性能的影响. HE等[21]提出基于协方差矩阵匹配构建稀疏信号恢复模型, 并证明利用阵列输出的二阶统计量可以获得更好的理论估计性能[22]. 然而, 这些参数离散化的方法无法避免在离散化间隔大小和计算复杂度之间的权衡问题. 为此, YANG等[23]通过估计无噪声协方差矩阵解决稀疏参数估计问题, 并提出基于协方差匹配的非离散化方法. LIAO等[24]利用协方差匹配误差的渐近分布特性构建非均匀噪声约束, 进而提出基于无噪声协方差矩阵低秩特性的非均匀噪声DOA估计方法. 然而, 上述基于协方差匹配的方法的估计性能往往依赖大量的快拍和较为准确的噪声先验知识.

基于协方差匹配的方法[23-24]本质上是通过对噪声协方差进行约束, 实现非均匀噪声的抑制, 然而,噪声统计量先验的准确性和渐近分布的多快拍数条件限制了其获取更好的DOA估计性能. 为缓解对非均匀噪声先验和多快拍数的依赖, 本文提出一种非离散化参数DOA估计方法, 即基于原子范数最小化和零化滤波器的方法(atomic norm minimization and annihilating filter, ANM-AF). 本文方法通过对信号协方差数据进行结构化约束, 实现在缓解噪声统计量先验知识依赖的同时抑制噪声影响, 并利用零化滤波方法缓解在少快拍条件下DOA估计精度下降的问题. 本文方法利用信号协方差矩阵的厄米特托普利兹结构和低秩特性构建结构化约束, 将非均匀噪声条件下的阵列信号协方差矩阵恢复问题转化为基于原子范数的低秩矩阵近似问题, 进而利用零化滤波性质将连续空间DOA估计问题转化为多项式求根问题. 仿真实验证明了ANM-AF可在非均匀噪声和少快拍条件下获得鲁棒的估计.

1 阵列信号模型

因而在少快拍数条件下, ΔR的渐近分布特性难以满足, 造成传统信号协方差矩阵估计出现较大误差, 进而严重影响DOA估计精度[26]. 因此, 本文利用原子集合刻画低秩矩阵, 从信号表示基元素的角度,构建不依赖快拍数和噪声先验知识的信号稀疏表示模型, 进而提高在少快拍和低信噪比条件下DOA参数估计的准确性; 并利用集合中描述稀疏性的参数在区间连续取值的特性, 在信号的稀疏表示和参数重构阶段均避免了参数的离散化[27], 进而可以有效抑制传统稀疏重构由离散化带来的网格误差.

2 原子范数

原子范数[28]作为逆问题求解的一种凸启发式方法, 可以利用最少原子构建信号参数的连续空间表示, 有利于避免在离散化间隔大小和计算复杂度之间的权衡问题. 在DOA估计的场景中, 因为连续空域中真实信源DOA的个数K是很少的, 因此, 可以利用原子范数来刻画这种空域稀疏性. 式(2)的阵列信号模型可以写成

若A为关于原点中心对称, 即a∈A当且仅当-a∈A , 那么 ‖·‖A就是一个范数, 称之 为X的原子范数. 原子集合A可以看成一个无限长的字典, 并且字典包含的方位参数可以在连续空间取值. 原子范数由于利用原子集合凸包的连续特性计算范数, 并在保证参数空间连续性的条件下构建信号稀疏性约束,因而从根本上避免了参数的离散化. 正因原子范数具备上述测量函数的性质, 所以X的原子范数‖X‖A是凸的.

3 本文方法

3.1 低秩矩阵近似的协方差矩阵估计

基于上述讨论, 利用信号协方差矩阵的厄米特托普利兹结构和低秩特性, 可将信号协方差矩阵的恢复问题转化为基于原子范数的低秩矩阵近似问题.首先, 将式(10)中基于秩函数表述低秩优化问题转化为实际可解的半定规划问题：

假设u∗表示式(13)问题的最优解, 那么根据上节所述, DOA参数可以由T(u∗)的范德蒙德分解唯一确定. 求解上述半定规划问题可以得到基于多快拍观测模型的阵列信号的估计Xˆ. 除了直接求解上述半定规划问题获得对原始信号的估计以外, 还可以通过对偶多项式来实现. 原子范数的对偶范数等价于原子集合A 的支撑集函数, 原子范数 ‖X‖A的对偶范数定义为

遵循拉格朗日分析[29], 上式对偶问题可转换为半定规划问题：

3.2 基于零化滤波器的DOA估计

因而信号功率的估计σˆ可以通过求解式(19)的线性方程组得到.

综上所述, 本文提出的基于低秩矩阵近似和零化滤波器的DOA估计方法步骤如下：

1)求解式(16)的半定规划问题, 得到信号协方差矩阵估计值T();

3)求解式(18)Z变换H(z)的 根以获得;

4)根据式(19)和(20), 确定DOA和信号功率的估计值和.

4 仿真结果

本文通过数值仿真检验本文方法在非均匀噪声、少快拍、低信噪比条件下的估计精度和鲁棒性. 在仿真中, 选取同类基于低秩矩阵的适用于非均匀噪声条件的DOA估计方法, 包括SPA[23]方法和LRMD[24]方法. 比较非均匀噪声背景下无偏估计的理论方差下限, 即克拉美罗界(Cramér-Rao bound, CRB). 本节采用均方根误差(root-mean-square error, RMSE)作为DOA估计精度的衡量标准, 定义为

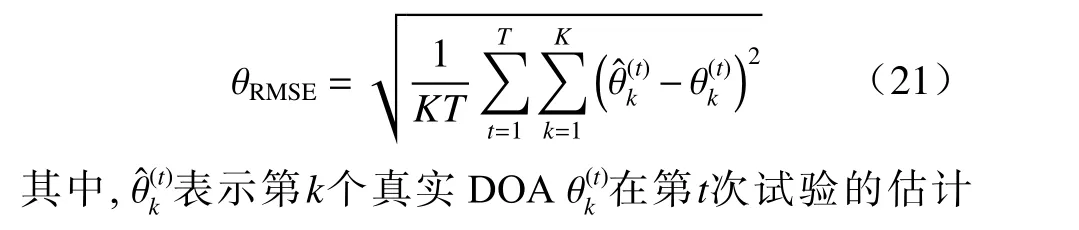
图1所示为在快拍数T=10、RSN=5 dB且 阵元噪声功率不一致条件下SPA方法、LRMD方法和本文ANM-AF方法的空间分布估计输出对比图. 图中幅度量纲为1. 由图1可知, 在少快拍条件下, LRMD方法的估计性能严重恶化, 估计信号方位和幅度均匀与真实值偏离较大, SPA方法和本文ANM-AF方法均实现了较为准确的DOA估计, 但本文ANM-AF方法更准确地实现了信号幅度的估计.

图1 少快拍条件下信号估计空间分布Fig. 1 Estimated signal spatial distribution in few snapshots

图2所示为快拍数T=10条件下DOA估计方法测向误差RMSE随SNR变化曲线. 根据图2的仿真结果可以发现, 在非均匀噪声背景下进行DOA估计,本文ANM-AF方法比其他方法更接近CRB, 在少快拍(T=10 )条件下具备更好的性能. 图3所示为RSN=5 dB条件下DOA估计方法测向误差RMSE随快拍数T变化曲线. 从图3的仿真结果可以看出, 本文ANMAF方法在非均匀噪声背景下的DOA估计性能对快拍数是鲁棒的, 并且在少快拍低信噪比条件下本文ANM-AF方法比其他方法具备更好的性能. LRMD方法虽然利用协方差矩阵的低秩特性, 但未利用其托普利兹结构; SPA方法虽然利用了托普利兹结构但其估计器相当于多快拍条件下的最大似然估计.本文ANM-AF方法从原子范数的角度刻画阵列信号的稀疏性, 进而将传统的信号协方差矩阵低秩恢复问题转化为基于原子范数的低秩矩阵近似问题, 进一步提升了基于矩阵低秩特性方法的性能.

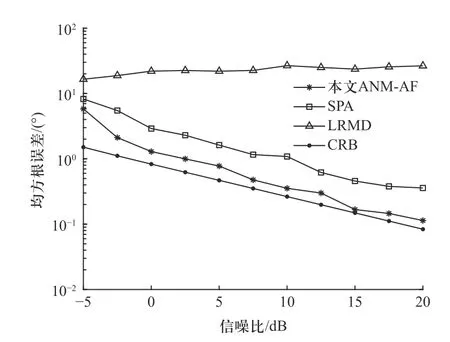
图2 RMSE随SNR变化Fig. 2 RMSE change with SNR

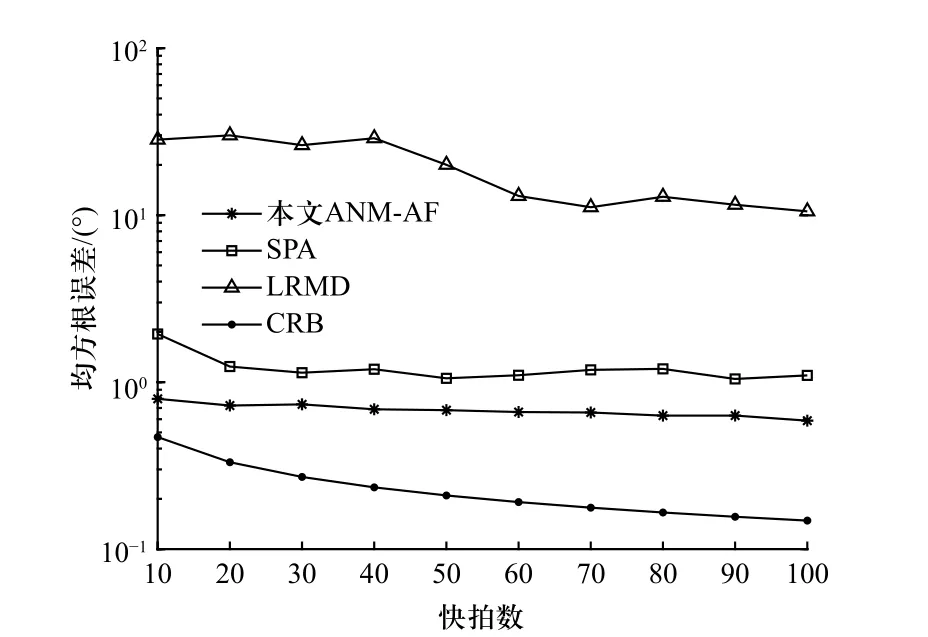
图3 RMSE随快拍数变化Fig. 3 RMSE change with snapshots

图4所示为T=10和RSN=5 dB条件下DOA估计方法测向误差RMSE随快拍数WNPR变化曲线. 仿真结果可以看出, 本文ANM-AF方法和SPA方法在少快拍和低信噪比条件下的DOA估计性能对阵元噪声的不一致性均是鲁棒的. 本文ANM-AF方法的估计误差曲线比其他方法更接近CRB, 在非均匀噪声环境变化的条件下具备更好估计性能的性能. 在不同最大噪声功率比条件下，本文ANM-AF方法的均方根误差H-SPA方法平均减小59.4%. LRMD方法利用加权采样协方差向量估计误差的渐近分布特性抑制非均匀噪声, 但这种渐近分布特性往往在快拍数达到较多的数量才近似成立, 因而在少快拍条件下该方法估计性能会严重恶化. SPA方法虽然并未明确指出利用了采样协方差估计误差的渐近分布特性, 但其采用的是基于协方差矩阵匹配的目标函数,而这种基于协方差矩阵匹配估计器的潜在假设是能够利用的渐近分布特性来抑制采样协方差估计误差[32], 进而实现对非均匀噪声的抑制, 然而, SPA方法本质上是多快拍条件下最大似然估计的实现[23].

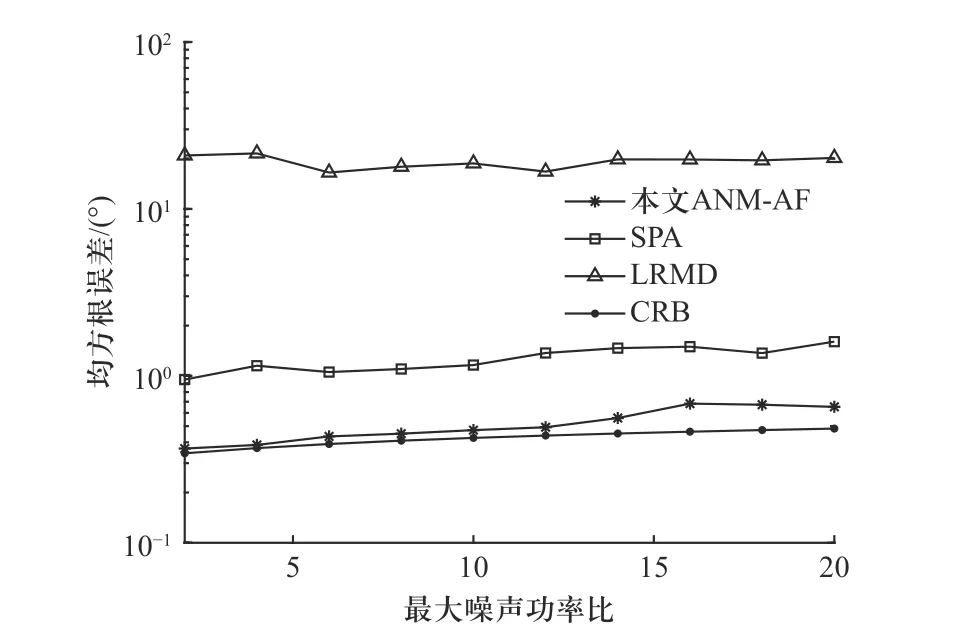
图4 RMSE随WNPR变化Fig. 4 RMSE change with WNPR

与上述其他方法不同, 本文ANM-AF方法不仅利用了信号协方差矩阵的厄米特托普利兹结构和低秩特性, 并且在信号参数连续空间的原子表示基础上, 构建不依赖快拍数和噪声先验知识的连续空间信号稀疏表示模型, 在信号的稀疏表示和参数重构阶段均避免了参数的离散化, 进而可以有效抑制传统稀疏重构由离散化带来的网格误差. ANM-AF方法不仅保持了适用于非均匀噪声环境的传统非离散化方法的特点, 而且增强了在少快拍低信噪比条件下的DOA估计性能.

5 结 论

针对传统非离散化方法在非均匀噪声和少快拍条件下DOA估计性能恶化的问题, 本文提出基于原子范数最小化和零化滤波器的非离散化参数DOA估计方法. 本文的原子范数最小化方法不同于传统方法对阵列信号一阶统计量进行约束, 而是对阵列信号二阶统计量进行结构化约束. 其利用信号协方差矩阵的厄米特托普利兹结构和低秩特性, 将非均匀噪声条件下的阵列信号协方差矩阵恢复问题转化为厄米特托普利兹矩阵的秩最小化问题, 进而转化为基于原子范数的低秩矩阵近似问题的求解, 实现信号协方差矩阵的估计. 针对传统方法在少快拍条件下DOA估计精度下降的问题, 本文进一步提出基于零化滤波器的DOA估计方法. 本文方法利用信号参数连续空间的原子表示描述阵列信号协方差矩阵,从模型假设上避免了对噪声统计量先验知识和快拍数条件的依赖, 不仅避免了传统基于稀疏表示的离散化方法在离散化间隔大小和计算复杂度之间的权衡问题, 而且克服了现有同类方法在非均匀噪声和少快拍同时存在条件下估计器性能恶化的问题. 因此, 对复杂环境下高性能估计方法的设计与实现具有重要借鉴意义.