某大型运输车的耐久性虚拟试验研究
2022-03-21荣吉利李先航王玺胡长华
荣吉利,李先航,王玺,胡长华
(1. 北京理工大学 宇航学院,北京 100081;2. 北京航天发射技术研究所,北京 100076)
大型运输车在国防领域应用越来越广泛,其具有载重大、自重轻、工作环境复杂、安全要求高等特点[1],在机动运输过程中需要经历严酷的振动与冲击环境,易造成关键部位或薄弱环节的损伤失效,一旦发生破坏会造成重大甚至灾难性的事故和损失. 因此,针对大型运输车的耐久性问题进行研究,具有重要的意义[2]. 车辆耐久性研究分为试验场外场试验、室内道路模拟实验和虚拟实验等[3]. 其中外场试验和模拟实验为实物实验,实验周期长、成本高[4-5]. 在产品设计阶段可以采用虚拟实验的方法,根据仿真计算结果优化产品设计,可以大大缩短设计周期,减少研制成本[6].
对于结构疲劳失效问题,国内外学者做了较多研究. LIAKAT等[7]提出了一种估算金属疲劳损伤演化和剩余疲劳寿命的实验方法,并对固体API 5L X52和1018碳钢管进行单轴拉伸-压缩实验,实验结果与预测结果吻合较好. 上述研究采用了准静态的计算结果,忽略了动态响应,不能真实地反映动态应力.
采用直接积分法对车辆进行动力学分析,获取车辆的时域动态响应,计算时间过长,而基于模态应力恢复理论的动力学计算方法可以快速获得车辆的时域动态响应. SHAO等[8]提出了一种基于实际矿山路面动态应变测量和有限元分析相结合的方法计算矿用自卸汽车驱动桥壳的疲劳寿命. 李飞[9]将实验与仿真相结合,对国内某A0级轿车的转向节进行了疲劳寿命预测研究,根据试验场试验获取了转向节的动载荷数据,并利用有限元法计算出应力谱分布,进行了疲劳寿命分析. 王卫东[10]建立了翻车机的刚柔耦合动力学模型,获取了翻车机靠板的各阶模态载荷时间历程,对靠板进行了疲劳寿命分析,并提出了改进靠板结构和材料的方法.
综上所述,针对所受激励较小、没有大范围变形、可以忽略非线性影响的结构,采用模态应力恢复法对其进行耐久性分析,可以获得比较准确的动态响应. 但研究者通常只将要研究的结构柔性化,并对其进行耐久性分析,而忽略了其他结构柔性的影响. 文中考虑车架柔性的影响,建立大型运输车整车刚柔耦合的动力学模型,基于模态应力恢复理论获得大型运输车在路面激励作用下的动力学时域响应,并对比仿真和实测垂向加速度的均方根值;利用有限元结果和动力学模态坐标结果,对车辆在D级路面上行驶进行耐久性分析,利用Ncode疲劳分析软件计算出上摆臂、下摆臂和力轴的疲劳寿命,并通过改进下摆臂结构,增加下摆臂的使用寿命.
1 模态应力恢复理论
在模态应力恢复理论中,柔性体被认为是其模态的集合,它的动态响应可以表示为其模态坐标和对应模态位移的线性组合. 因此,柔性体的的广义坐标可以表示为

式中,Eσ为模态应力矩阵,由有限元模型的模态分析获得. 因此,将模态分析结果作为耐久性分析的有限元输入,模态位移结果作为耐久性分析的载荷输入,可以对车辆进行耐久性分析.
2 整车静力学分析
2.1 柔性体模型
大型运输车主要由行驶系统、传动系统、上装质量和其他系统构成. 行驶系统包括悬架、车架、轮胎,其中,悬架由上摆臂、下摆臂和力轴构成. 在不改变载荷传递的前提下,将上装质量和传动系统简化为质量点,分布在车架回转支耳和外支耳上.
采用双横臂悬架系统,车架、上摆臂、下摆臂和力轴之间建立铰接,油气弹簧的两端分别连接车架和下摆臂,力轴与地面参考点通过弹簧连接单元连接,以代替轮胎模型. 在Abaqus中建立有限元模型如图1所示. 车体结构的材料为HG785,其密度为7 800 kg/m;杨氏模量为210 MPa;泊松比为0.3;屈服强度为685 MPa;抗拉强度为785 MPa.

图1 整车有限元模型Fig. 1 Finite element model of whole vehicle
2.2 静力学分析
对地面参考点施加固定约束,对整个模型施加重力,并进行静力学分析. 图2为车架垂向位移云图,由于上装质量集中在车架后方,车架前梁翘起,但垂向位移仍是负值,车架最大下沉量出现在尾梁,达到128.2 mm. 由图3可知,整车处于低应力水平,大部分节点应力值在30 MPa左右;由图4所示,最大应力出现在车架4桥左侧力轴,应力值为103.6 MPa,远低于HG785的屈服应力值.

图2 车架垂向位移云图(放大50倍)Fig. 2 Vertical displacement contour of frame(scale 50)

图3 整车应力云图Fig. 3 Stress contour of whole vehicle

图4 4桥右侧力轴应力云图Fig. 4 Stress contour of right 4 force axis
2.3 模态分析
为了获取柔性体结构的动力学特性,在ABAQUS中对其进行模态分析,求解模态频率和振型,并生成含应力信息的中性文件. 表1给出了4种结构的前6阶非刚体模态频率.

表1 前6阶非刚体模态频率Tab. 1 The first 6-order non-rigid modal frequencies Hz
3 整车动力学分析
3.1 路面模型
车辆在行驶过程中,路面不平度是产生激励的最主要原因,通常用功率谱密度描述[11]. 在一段空间频率n内,运用指数函数拟合出路面不平度功率谱密度Gq(n),其表达式为

式中:n为空间频率,表示单位长度中包含几个波长,单位m-1;n0为参考空间频率,数值为0.1 m-1;Gq(n0)为参考空间频率n0下的路面谱值,称为路面不平度系数,单位为m2/m-1=m3;W为频率指数,一般取2. 我国根据上述方法将路面分成了8个等级,并规定了各等级路面Gq(n0)的几何平均值及上下限,如表2所示.
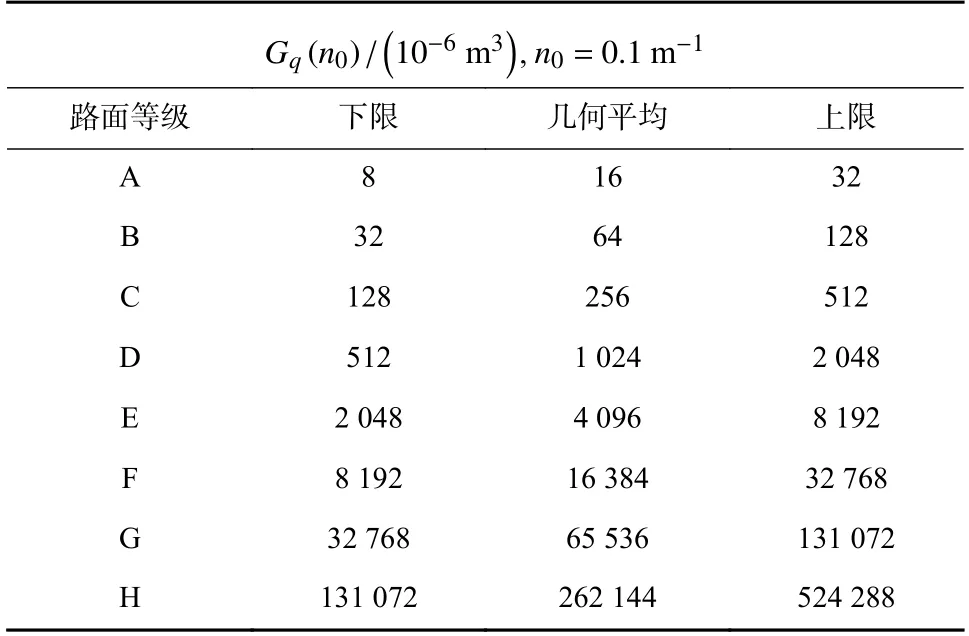
表2 路面不平度8级分类标准Tab. 2 Grade 8 classification standard of road roughness
路面模型的构建方法有三角级数法、AR/ARMA法、白噪声法、过滤泊松过程法等[12-13]. 在理论上任意路面都可由一系列离散的正弦波叠加而成,三角级数法可以对任意路面进行重构[14]. 文中采用三角级数法建立路面模型,其表达式为

式中:q(x)为 路面不平度与空间位置的关系;Gqi为路面功率谱时域区间划分n个小区间的中心频率谱密度值;θi为 随机数据,其区间为0~2π,呈均匀分布.
利用三角级数法构建D级路面模型,其路面不平度-位移曲线和功率谱密度曲线如图5和图6所示.

图5 D级路面不平度-位移曲线Fig. 5 Roughness displacement history of grade D road
图6中直线为标准路面功率谱密度上下限,曲线为生成路面的功率谱密度,由图可知,当路面频率在0.01~2.83 m-1区间内,路面模型功率谱密度大部分位于标准路面的上下限之间,验证了路面模型的正确性.

图6 D级路面功率谱密度曲线Fig. 6 Power spectral density of grade D road
3.2 动力学模型
在Adams软件中导入车架、上摆臂、下摆臂和力轴中性文件以及路面模型,并建立相应的连接关系,油气弹簧的等效刚度为106N/m,等效阻尼为8 000 N·s/m;轮胎选用FIALA模型,等效垂向刚度为106N/m,等效垂向阻尼为2 000 N·s/m,并与力轴建立旋转副约束,总装形成刚柔耦合动力学模型,如图7、图8所示.

图7 轮胎和悬架系统Fig. 7 Tire and suspension system

图8 整车动力学模型Fig. 8 Dynamics model of whole vehicle
3.3 动力学分析
车辆的激励主要来源于路面不平度,轮胎与路面之间设置接触关系,车辆的行驶速度通过力轴与轮胎的旋转副驱动控制. 为了验证模型的准确性,利用三角级数法构建了平坦路面模型,如图9所示,并对车辆以65 km/h的速度在平坦路面行驶进行了动力学仿真.
图9 平坦路面不平度-位移曲线Fig. 9 Roughness displacement history of flat road
如图10所示,车辆从静止出发,在7.5 s左右达到预定速度并保持不变. 对车辆在10~40 s稳定速度的仿真结果进行分析,选取位于车架前桥和后桥之间测点的垂向加速度值,与实测数据进行对比.

图10 平坦路面行驶速度曲线Fig. 10 Speed time history on flat road
图11和图12分别给出了测点的垂向加速度仿真曲线和实测曲线,由图可知,仿真结果与实测结果大致相同;表3统计了垂向加速度的均方根值,可知仿真结果与实测结果的误差为4.1%,验证了模型仿真计算的正确性.
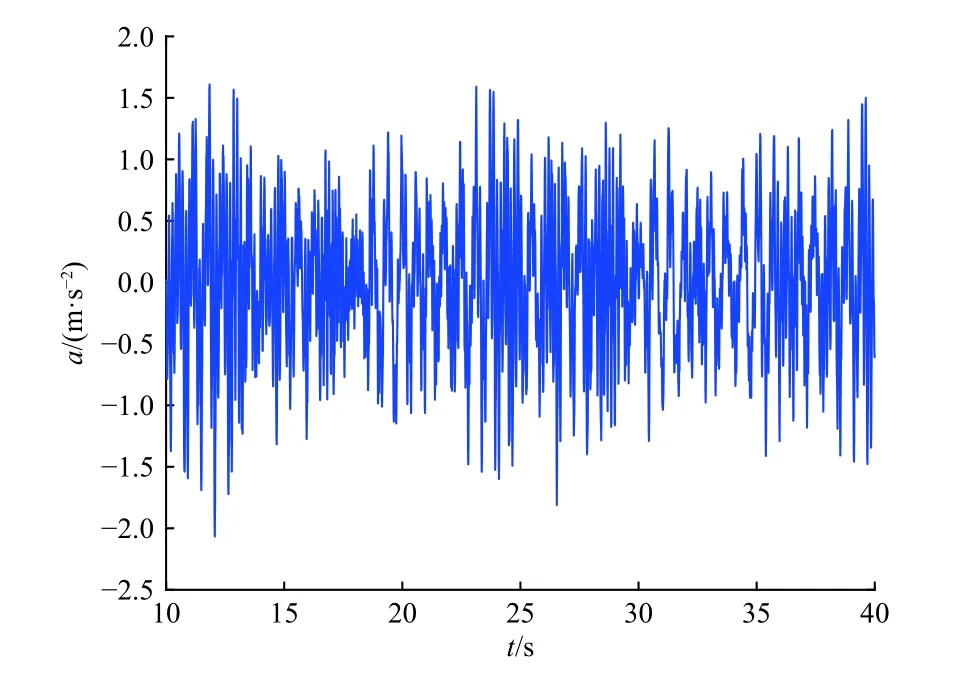
图11 垂向加速度仿真曲线Fig. 11 Simulation result of vertical acceleration-time history
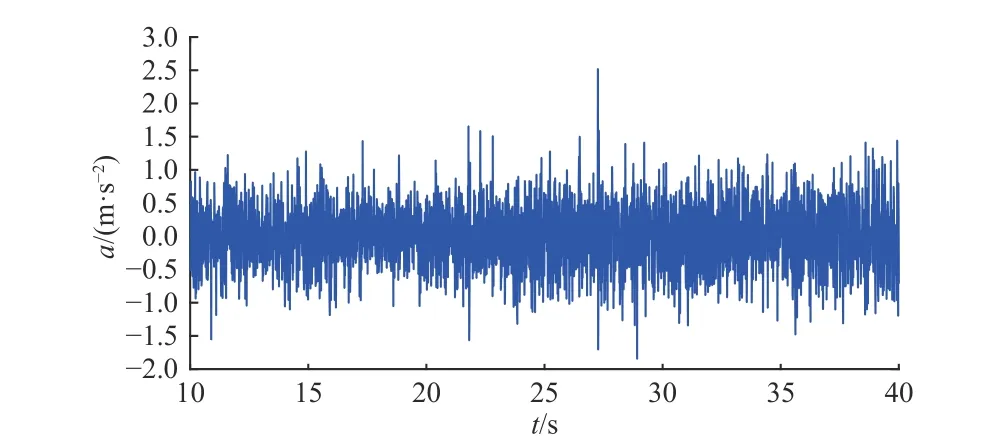
图12 垂向加速度实测曲线Fig. 12 Measure result of vertical acceleration-time history

表3 垂向加速度对比Tab. 3 Comparison of vertical acceleration
4 悬架耐久性分析
4.1 耐久性分析方法
对结构进行耐久性分析通过计算其疲劳寿命实现,采用Ncode软件进行疲劳寿命计算需要设置材料的S-N曲线,并且需要结构的有限元分析结果和载荷谱作为输入.
4.1.1 材料S-N曲线
车辆结构疲劳失效一般属于高周疲劳,通常使用幂函数公式拟合材料的S-N曲线,在双对数坐标系下循环次数和循环应力呈线性关系.
车体材料的抗拉强度为785 MPa,可以根据材料的抗拉强度σb估算其S-N曲线,由于估算材料S-N曲线放大了循环应力对疲劳寿命的影响,所以计算得到的疲劳寿命会更加保守. 由于悬架系统主要承受弯曲载荷,当循环次数N=103时, σ103=0.9σb;循环次数N=106时, σ106=0.5σb. 因此,估算材料的SN曲线在双对数坐标系下如图13所示.
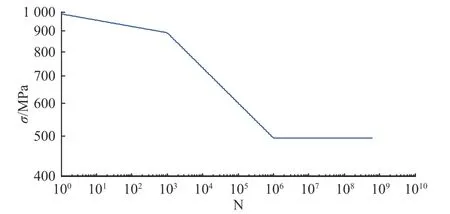
图13 HG785材料S-N曲线Fig. 13 S-N curve of HG785
4.1.2 载荷谱
根据我国公路等级的规定,四级公路是路面等级最低的公路,行车限速为20~60 km/h,其功率谱密度处于D级路面不平度的范围内. 因此,文中对在D级路面以60 km/h速度行驶的车辆进行了疲劳寿命分析,通过动力学计算,获得上摆臂、下摆臂和力轴在30 s内的模态坐标变化情况,可作为耐久性分析的载荷谱输入,图14给出了1桥左侧上摆臂的模态坐标历程曲线,该曲线反映了1桥左侧上摆臂结构第7阶自由模态(第1阶非刚体模态)在动力学响应中的参与量.
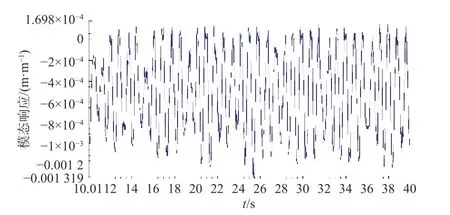
图14 1桥左侧上摆臂模态坐标曲线Fig. 14 Modal coordinates time history of left 1 upper swing arm
4.1.3 损伤计算方法
选用Von Mises应力作为计算标准进行疲劳分析,考虑了平均应力的符号对疲劳寿命的影响,选择Goodman修正方法对应力幅值进行修正.
文中采用Palmgren-Miner准则计算结构的总损伤,认为结构在一段时间内的总损伤是所有应力循环造成损伤的线性累计,是工程中最广泛使用的损伤计算方法.
4.2 疲劳寿命计算
利用含应力信息的模态分析结果和30s的模态坐标曲线对车辆的上摆臂、下摆臂和力轴进行寿命分析,得到其疲劳寿命分布云图.
4.2.1 上摆臂疲劳寿命
对上摆臂进行疲劳寿命分析,4桥右侧上摆臂结构寿命最小. 如图15所示,由于上摆臂两端是铰接约束,可以转动,两端承受载荷较低,中间位置承受载荷较高,寿命较小,易发生疲劳破坏,最小寿命为2.55×1011循环.
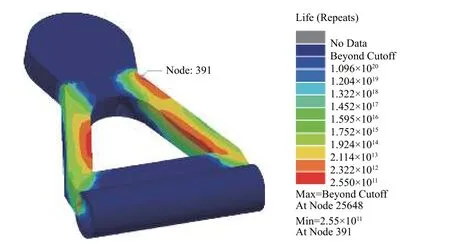
图15 4桥右侧上摆臂寿命云图Fig. 15 Fatigue life contour of right 4 upper swing arm
4.2.2 力轴疲劳寿命
对力轴进行疲劳寿命分析,4桥右侧力轴寿命最小. 如图16所示,力轴的圆柱结构基本没有损伤,上下两侧载荷较大,易产生疲劳破坏,其中与上摆臂连接一侧的寿命最小,为2.244×1011循环.
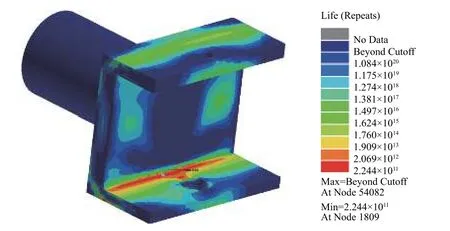
图16 4桥右侧力轴寿命云图Fig. 16 Fatigue life contour of right 4 force axis
4.2.3 下摆臂疲劳寿命
对下摆臂进行疲劳寿命分析,4桥右侧下摆臂寿命最小. 如图17所示,下摆臂外侧与力轴相连,受到铰接约束,可以转动,基本没有损伤;与车架铰接的圆孔及附近区域受到弯曲载荷比较明显,部分结构出现应力集中,导致疲劳寿命较小,最小寿命为1.599×106次循环.

图17 4桥右侧下摆臂寿命云图Fig. 17 Fatigue life contour of right 4 lower swing arm
通过对悬架结构的疲劳分析,发现4桥的悬架结构疲劳寿命最小,最易产生疲劳破坏. 这与静力学分析结果中4桥应力水平最高相符. 在悬架系统中,由于下摆臂结构出现应力集中,导致其寿命较低,因此需要对下摆臂结构进行改进.
4.3 下摆臂结构改进
通过对下摆臂最小寿命节点所处的位置进行分析,发现直线相交的结构会引起应力集中,导致寿命明显减少;对其结构进行改进,在相交处增加倒角,并进行疲劳寿命分析,结果如图18所示,寿命分布云图基本一致,最小寿命为1.167×107循环,相比改进前结构,最小寿命提升了大约7.2倍.
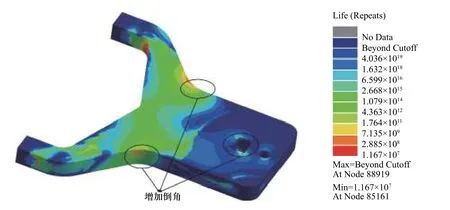
图18 改进后下摆臂寿命云图Fig. 18 Fatigue life contour of improved lower swing arm
5 结 论
车辆实物耐久性试验周期长、成本高. 文中建立了多轴特种车有限元模型,对车辆进行了静力学分析和模态分析;建立了整车刚柔耦合动力学模型,进行了动力学分析;根据模态应力恢复理论,对车辆上摆臂、下摆臂和力轴进行了疲劳寿命分析,所得到的疲劳寿命对车辆的设计、寿命预测提供了参考.
由静力学分析结果可知,只在重力作用下,车架尾梁的下沉量明显大于前梁,悬架结构的应力水平高于车架,最大应力明显低于材料的屈服强度;
车辆在平坦路面行驶的动力学仿真计算结果与实测结果比较符合,垂向加速度均方根值相差4.1%,此模型可用于后续耐久性分析;
对悬架的3种结构进行了耐久性分析,疲劳寿命结果表明4桥的悬架结构寿命最小,其中下摆臂结构由于应力集中寿命明显低于其他结构,在实际应用中要避免出现应力集中现象;
通过增加倒角改进了下摆臂结构,减弱了应力集中现象,下摆臂的疲劳寿命增加了7.2倍左右.
