新鲜度限制约束下物流配送中心选址-路径优化

刘琳，贾鹏，高犇，赵雪婷

新鲜度限制约束下物流配送中心选址-路径优化

刘琳a，贾鹏b，高犇c，赵雪婷c

（大连海事大学 a.交通运输工程学院 b.综合交通运输协同创新中心 c.航运经济与管理学院，辽宁 大连 116026）

满足生鲜产品交付时较高的新鲜度要求，解决多产品、多车型情景下的配送中心选址-路径优化问题。构建考虑碳排放成本和满足客户对产品交付最低新鲜度要求的双层目标规划模型。上层模型以配送中心固定成本、库存管理成本最小化为优化目标，下层模型以车辆固定成本、运输成本、碳排放成本、惩罚成本最小化为优化目标，并结合模型特点，采用两阶段启发式算法进行求解。采用的两阶段启发式算法相对于遗传算法的平均成本解改进率为1.22%，相对于K-means聚类求解算法的平均解改进率为3.03%；两阶段启发式算法相对于遗传算法最优解运算时间的平均提高率为24.8%，相对于传统K-means聚类求解算法的平均提高率为33.0%。经算例对比研究发现，不同新鲜度要求下对配送中心的选址以及车辆路径的安排有显著影响，企业可通过合理规划物流网络和准确评估客户对产品的新鲜度要求等手段实现企业物流成本的降低。

选址-路径问题；新鲜度约束；物流配送中心；双层目标规划模型

近年来，依托于互联网的高速发展，生鲜电商开始进入发展的黄金时代。结合生鲜产品容易腐烂、易于变质、时效性要求高等特点，对其交付的及时性和交付时的新鲜度提出了很高的要求。若交付时产品的质量明显下降，通常将直接被拒收。这就需要一个完善的物流系统来支撑，通过合理的物流系统规划来缩短产品的交付时间，保障产品的质量，同时又可以降低成本。配送中心选址及车辆路径规划是物流系统2个重要组成部分，两者之间既相互独立又彼此关联，不能割裂看待，企业应该追求的是整体最优而不是局部最优。由此可见，应对传统生鲜产品的单一选址问题、单一配送进行扩展，将两者综合考虑，并且引入多种生鲜产品、多种车型，这样与现实情况更加贴近。

结合该类产品特点，为了保障产品交付质量，考虑生鲜产品的新鲜度受到很多学者的关注。杨晓芳等[1]针对三级冷链物流网络配送中心的选址问题进行了研究，构建了以追求物流成本最小化和客户满意度最大化的双目标模型。陈绍洵等[2]为解决生鲜产品终端配送难题，研究了生鲜自提柜选址问题，建立了考虑货损成本的双层目标规划模型，并证实产品的新鲜度对生鲜自提柜的选址有显著影响。吴芳芸等[3]针对生鲜品小批量、多频次的配送特点，为了提高车辆的装载率，降低成本，研究了冷链背景下轴幅式物流网络，引入运输时间约束，并设计了新鲜度分段函数，构建了以时效最优、成本最低的物流网络模型。李善俊等[4]研究了单一配送中心、单一生鲜产品、时间窗约束条件下的配送路径规划问题，构建了最小化配送总成本和最大化生鲜品新鲜度的多目标优化模型。P. Amorim等[5]针对易腐品车辆路径问题，构建了分销成本最小化、交付产品新鲜度最大化的双层目标规划模型。以上都是针对单一生鲜产品进行研究，杨霞等[6]研究了软时间窗约束下多种生鲜产品的车辆路径规划问题，引入了新鲜度阈值，并利用插点分段的方法衡量曲线上两客户点间距离，建立了系统总成本最小化的优化模型。张倩等[7]更全面地考虑了多种车型，研究了不确定需求下配送路径优化问题，建立了总成本最小化、产品新鲜度最大化、碳排放量最小化的配送路径多目标优化模型，促进了冷链物流的绿色化，实现了经济与环境协调发展。顾莹等[8]研究了多种产品配送路径优化问题，考虑了冷藏车、常温车等2种车型，构建了行驶成本最小化和客户满意度最大化的双目标模型。

同时，越来越多的学者意识到选址和配送是物流系统中2个重要的模块，两者之间既相对独立又彼此关联，不能割裂看待，企业应该追求整体最优而不是局部最优。在非生鲜产品的背景下，陈松岩等[9]以货物从供货商，经配送中心，最终到达客户的整个物流活动成本最小化为目标，确定了供货商、配送中心的位置及数量，规划配送中心到客户的最优配送路径。石兆等[10]研究了三级物流网络中配送中心的选址及供应商、配送中心车辆行驶线路规划问题，并在模型中引入了配送中心和客户服务时间窗约束，考虑了多种车型，基于改进最小包络聚类法和遗传算法的优越性求解模型。罗耀波等[11]更全面考虑了仓库容积约束，并设计了模糊时间窗，以适应顾客弹性预约服务时间偏好，建立了以总费用最小化、客户满意度最大化的双目标选址-路径模型，构造两阶段模拟退火算法进行求解。在生鲜产品背景下，杨海兰[12]引入了混合时间窗，构建了总成本最小化，客户满意度、客户价值最大化的冷链物流选址-路径多目标规划模型。杨晓华等[13]研究了在客户需求量、退货量不确定的情况下，考虑了多周期、同时取送的生鲜产品闭环物流网络问题，并基于相同的算例数据，验证了多周期物流配送系统比单周期更能均衡多决策安排。李冰等[14]研究了多配送中心、单一车型等条件下，生鲜产品同时取货的选址-路径问题，综合考虑了取、送货时间窗及产品损耗，通过算例分析验证了同步取送相对于取送分离模式的优越性。

选址-路径问题（Location Routing Problem，LRP）是选址定位问题（Location Allocation Problem，LAP）和车辆路径问题（Vehicle Rounting Problem，VRP）的组合问题，两者都属于NP-hard，基于此，考虑时间窗的选址-路径问题（Location Routing Problemwith Time Windows，LRPTW）更为复杂。在大部分情况下，利用精确算法来求解LRPTW问题存在困难，一些学者选择采用两阶段启发式算法进行求解[10,15-17]。姬杨蓓蓓等[15]利用两阶段启发式算法求解快递企业末端配送网络规划问题，第1阶段利用K-means进行聚类，第2阶段利用蚁群进行路径规划。当前，比较常用的聚类方法都是根据配送中心到客户的空间距离来划分配送中心负责客户点的范围。这种方法虽然简单但是聚类效果较差，特别是在求解带时间窗的选址-路径问题时。基于以上背景，于滨等[16]设计了聚集度启发式分类算法，引入了确定性信息和启发式信息，在进行客户分类时，一方面衡量客户点空间距离及时间窗相似性，另一方面考虑了先前分类的经验，提高了分类效率。Xuping Wang[17]引入了时空距离的概念，通过计算客户间的时空距离，并结合遗传算法对客户点进行聚类，生成初始解。

综上所述，现有针对生鲜产品的选址-路径问题均以单一车型、单一产品为主，但是现实情况下，企业往往具有多种不同载质量的车型，以适应客户的不同需求。同一客户同时需要多种生鲜产品，与现实情况更为贴近。以往的生鲜产品的选址路径都是通过考虑客户时间窗，以及在目标函数中引入货损成本，追求目标函数最小化，来提高交付时产品的新鲜度。由于生鲜产品的特殊性，客户对交付时产品的新鲜度有较高的期望。若交付时产品的质量明显下降，通常将直接被拒收。由此，将产品交付时的新鲜度大于客户要求的最低新鲜度作为一个必要条件存在于模型中是十分有意义的，文中在考虑客户时间窗和交付产品新鲜度的基础上，建立具有最低新鲜度限制的多种生鲜产品、多种车型的选址-路径优化问题的双层目标规划模型。基于模型特点，运用两阶段启发式算法，在满足客户要求的条件下，实现物流系统总成本的最小化。

1 模型构建

1.1 问题描述

文中的研究对象是由多个备选配送中心和多个客户点构成的物流系统。每个配送中心内含有多种相同的生鲜产品，分别有1支车队负责完成客户的配送任务，每支车队均含有A、B、C等3种车型。每个客户点同时需要多种生鲜产品，每种产品的有效生命周期不同，交付时每种产品的新鲜度都需满足客户最低新鲜度的要求。候选配送中心、客户点的数量、客户点位置、每个客户点的需求量、服务时间窗等信息均已知。车辆从配送中心始发，前往各客户点，等待客户完成装卸后继续行驶到下一个客户点，最终返回配送中心。每辆车最多行驶1条路径，但是每条路径上可以有多个客户点。在满足客户需求量、交付时间窗、最低新鲜度和车辆承载能力的要求下，确定配送中心的位置及配送路径，最终实现总成本的最小化。

1.2 模型假设

为了求解问题，建立了如下基本假设。

1）每辆车只服务于1条路径，每辆车1次可以配送多个客户的订单。

2）每个客户只有1个配送中心和1辆车为其提供服务。

3）每个客户的需求在1次配送中得到满足。

4）配送中心有多种车型，车辆总数能完成配 送任务，任意车型的载质量都不小于单个客户的需求量。

5）假设商品从离开配送中心那一刻起，新鲜度就开始衰减，交付客户的产品必须满足最低新鲜度的要求。

6）所有车辆都从配送中心出发，服务完路径上的客户后再返回配送中心。

1.3 符号说明

1.4 相关指标计算

1）CO2排放量计算。根据文献[18]计算燃料消耗量，其可以表示为：

(1)

(2)

2）新鲜度计算。对于任意一种易腐品，随着时间的推移，产品新鲜度会不断衰减。文中采用单调连续递减函数来描述产品新鲜度随时间的变动情况[19]。假设产品其新鲜程度在离开配送中心后就会衰减，设产品离开配送中心为0时刻，交付客户为时刻，产品的新鲜度可以表示为：

(3)

当产品送达时，若产品新鲜程度明显下降，客户会直接拒收这批产品，因此交付时必须要满足客户的最低新鲜度的要求，即：。

1.5 双层规划模型

1）上层模型。

(4)

S.t(5)

(6)

(7)

上层目标函数式（4）表示最小化配送中心的固定成本和仓库管理成本，式（5）表示配送中心的开设数量不能超过最大开设数量，式（6）表示决策变量的取值范围，式（7）表示每个客户总需求量为各种产品需求量之和。

2）下层模型。

(8)

S.t(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

2 求解算法

文中运用两阶段启发式算法[16,20]，第1阶段利用聚集度的启发式算法，对客户点进行聚类，初步确定每个客户点对应为其提供服务的配送中心，从而实现多中心选址-路径问题向多个单中心路径问题的转换，降低了问题难度；第2阶段利用改进蚁群算法规划相应的配送路线。具体算法流程见图1。

首先，确定仓库的位置和数量以及所有客户点的分类，具体步骤如下所述。

其次，完成所有客户点的初始划分后，利用蚁群算法，规划每个被选配送中心服务客户点的配送路线，以单独一个配送中心为例，具体步骤如下所述。

Step1：蚂蚁从配送中心出发，计算可行集内客户点被访问的概率，根据轮盘赌选择法得到下一个要访问的客户点，并分配可获得的车辆。

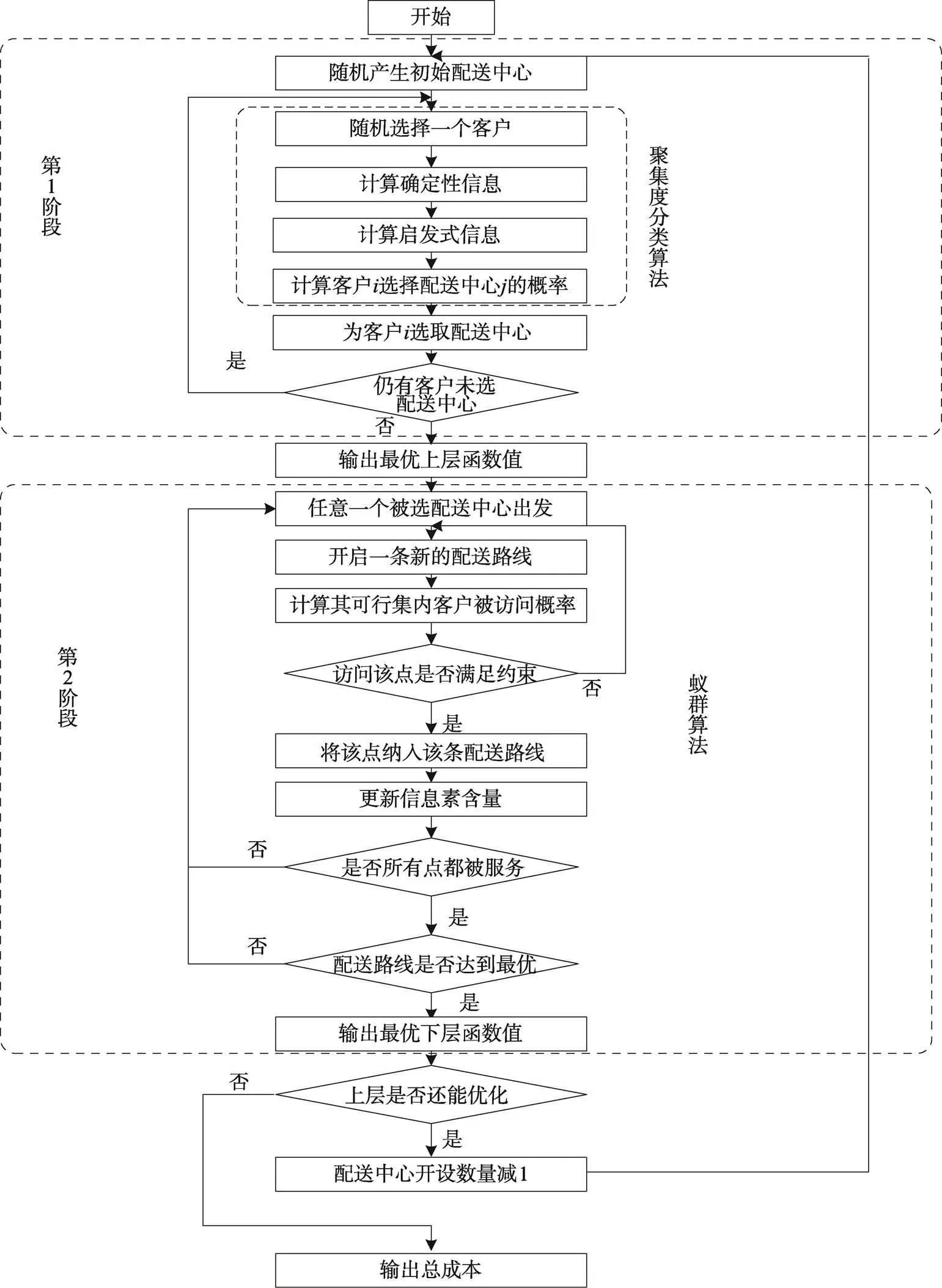
图1 算法流程

Step2：依次确定该条路线后续访问的客户点，并满足车辆的容量、距离限制、交付最低新鲜度限制，否则，转至Step3。

Step3：重新开启其他新的路线，直到完成其服务范围内所有点的配送。

Step5：在不改变所选配送中心及客户点划分的条件下，将每次得到的新的下层目标函数值与原最优值进行对比，若新函数值小于原，则更换，并重新开始下一次路径优化，直到超出允许最大迭代次数。

再次，保持配送中心开设数量不变，产生新的选址方案，重新计算上层成本。如果得到的成本小于则跳转到第2部分；否则将配送中心开设数量降低1个，在减少配送中心的数量的同时必须满足配送中心的容量约束。如果最后找不到满足容量约束的配送中心方案，则结束算法。

2.1 聚集度的启发算法进行客户聚类

广泛使用的客户聚类方法根据客户与配送中心的距离进行分类，但是在面临带有时间窗的问题时，这种方法会产生的解质量不高。由此，文中在对客户进行聚类时，引入了2种信息。

(27)

(28)

(29)

(30)

(31)

2.2 蚁群算法进行路径规划

蚁群算法（ACO）本质上是一个基于信息正反馈原理的智能算法，并且具备较强的鲁棒性、良好的分布式计算机制等优势。蚁群算法常用来解决单配送中心车辆调度问题，并取得了较好的成效。文中首先利用基于聚集度的启发式算法，将多配送中心选址路径问题转化为多个单配送中心车辆调度问题，从而应用蚁群算法进行车辆路径的安排。文中按照以下4个方面设计算法，从而确定配送路径。

1）方案构造。从某配送中心出发，途经服务范围内所有的客户点，最终返回此配送中心，此路线即构成一个方案。同时每个客户有且仅被服务1次，满足每个客户的时间窗要求，交付时每个客户每种产品的新鲜度必须大于最低新鲜度，每辆车载重不能超过最大承载能力。基于车辆行驶路径的顺序进行编码。例如从配送中心1出发，先后经过客户点10、12、20、15，最后返回配送中心1，该路线的编码为1-10-12-20-15-1。

2）转移规则。蚂蚁从配送中心出发，根据式（32）得到每个客户点被访问的概率，根据轮盘赌选择法得到下一个要访问的客户点；然后计算，如果访问这个客户点，是否会超出车辆的各种最大限制约束和新鲜度约束限制，如果满足，则将该客户点加入路径中；否则，该车路径结束，下一辆车继续从配送中心出发。节点选择节点作为下一个配送点的概率的计算见式（32）。

(32)

3）交叉算子。为了有效控制算法陷入局部收敛，利用交叉算子拓宽解空间的搜索范围。依据交叉率从解决方案中随机选择路径，从被选路径 中各自随机选择1个位置进行交叉，构造新的解决方案。

4）信息素更新。每完成1次循环后，都需要更新蚂蚁走过路径上的信息素含量，计算见式（33）。

(33)

(34)

3 数值实验

3.1 基础数据

为验证模型的有效性和正确性，实验算例如下：某个供货商A作为多种生鲜产品的一级经销商，其供给的产品有稳定的销路，主要负责为区域内多个地区的24个二级经销商供货，供货频率为每月1次，并针对单个周期进行研究。由于产品的特殊性，对产品时效提出了很高的要求，为了缩短交付时间，保障产品交付时的新鲜度，供货商A决定从当前8个候选配送中心中筛选若干建立配送中心，完成产品的周转工作。设定每个配送中心的使用寿命为20年，每个配送中心的容量、建设成本、月分摊成本、月单位库存管理费用详见表1。每位客户对产品的需求种类数为2～3，对每种产品的需求量和服务时间窗详见表2。每个配送中心均可以提供a、b和c等3种产品，其有效生命周期分别为9、6、4 d，并拥有A、B、C等3种不同车型用来承担相应的运输任务，详见表3。各路段的长度为节点间的欧式距离，车辆在路段上匀速行驶，平均速度=60 km/h，单位时间车辆的等待成本和惩罚成本分别为=10，=20。燃油转换系数=2.62，碳排放成本=0.004元/g，配送中心允许开设的最大数量=6。

表1 配送中心相关参数

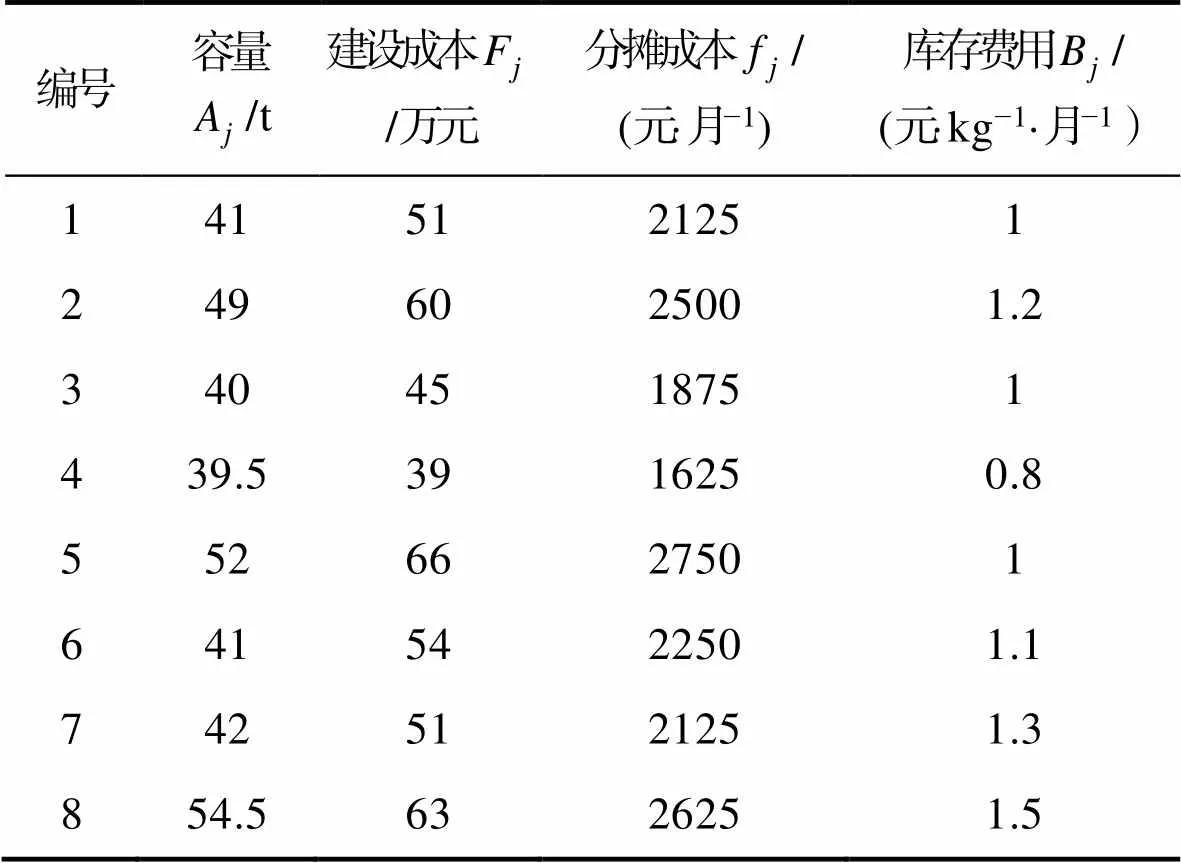
Tab.1 Relevant parameters of distribution center

表2 客户需求的相关参数

Tab.2 Relevant parameters of customer demand

表3 不同车型相关参数

Tab.3 Relevant parameters of different vehicle models

3.2 结果分析

相关数据[20]设置如下：种群数量为100；最大迭代代数为150；控制参数=1；=3；信息保留程度=0.95；控制参数=2000；蚂蚁每完成1次循环产生的信息总量=1500；启发式因子=1；=3；交叉概率=0.01；3种产品的最低新鲜度均为0.75。文中在AMD A6-5345M APU with Radeon(tm) HD Graphics 2.20 GHz内存为4 GB的电脑上，利用Matlab 2016a软件运行程序，得到相应的配送中心选址和运输路径结果，运行结果见表4、图2。

同时，基于相同数据背景对比分析3种算法的运行结果，分别包括：文中所采用的两阶段启发式算法（算法1）和遗传算法（算法2），以及传统利用k-means进行聚类的两阶段启发式算法（算法3），并进行了多组实验，每组设置不同的值，每组实验均进行15次，得到3种算法的运算结果详见表5。

表4 运算结果

Tab.4 Operation result

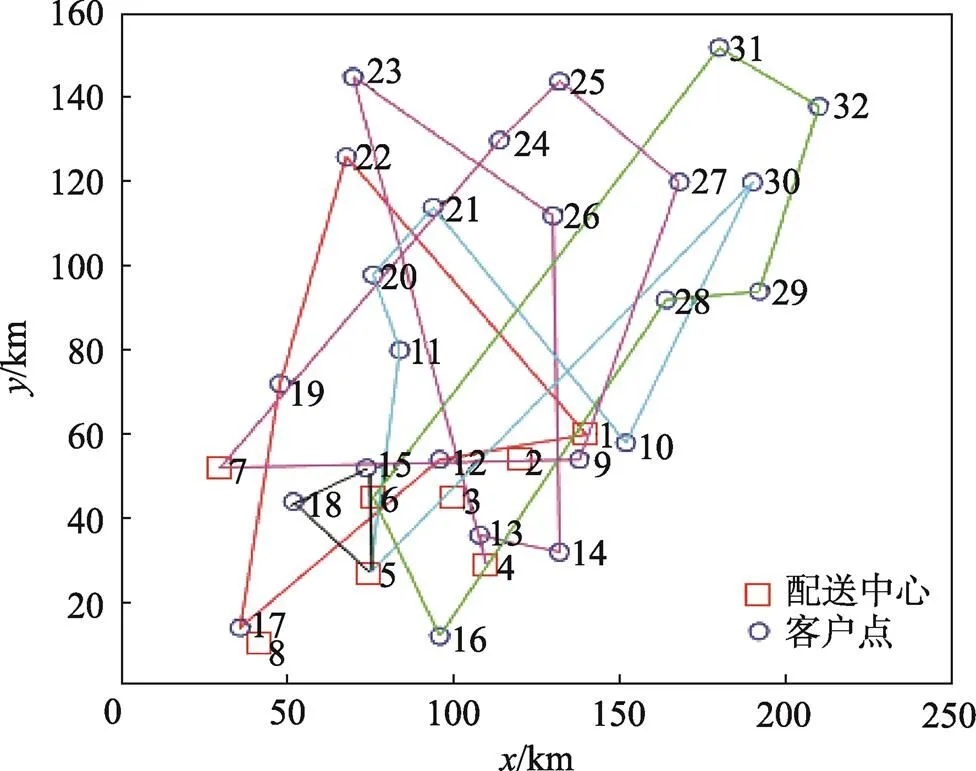
图2 最优选址及路径分配方案

为了进一步验证两阶段启发式算法对于求解两阶段问题（选址-路径问题）的优越性，并结合文中考虑客户交付时间窗的问题背景，着重对算法1和算法2的最优方案收敛图进行了对比，详见图3。

表5 各算法运行结果

Tab.5 Results of each algorithm

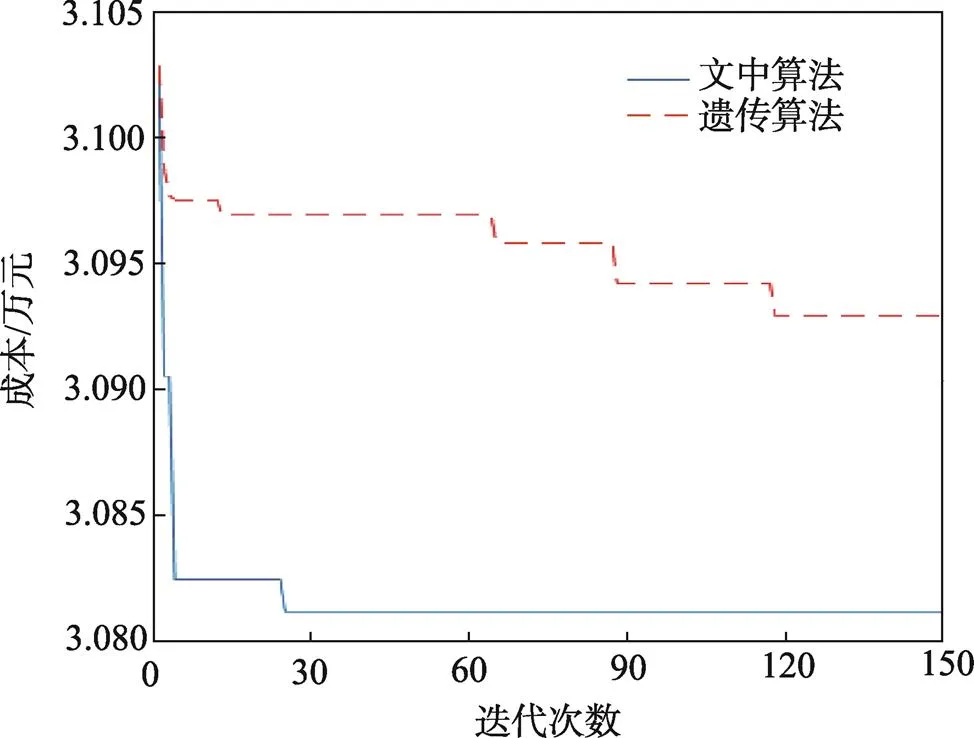
图3 算法迭代

如图3所示，遗传算法不仅收敛速度慢，而且容易陷入局部最优，求解质量较差。文中采用的算法在收敛速度和解的质量方面都具有一定的优越性。

3.3 敏感度分析

为了分析交付时产品最低新鲜度约束对结果的影响，利用上述数据进行多组实验，在其他数据保持不变的情况下，以新鲜度值等于0.55时为起点，以相邻2个新鲜度值相差0.1为间隔，进行敏感度分析，输出了1组成本折线图，从而更清晰地了解随着交付新鲜度的增加，以及总成本、上层成本、下层成本的变化情况，详见图4。

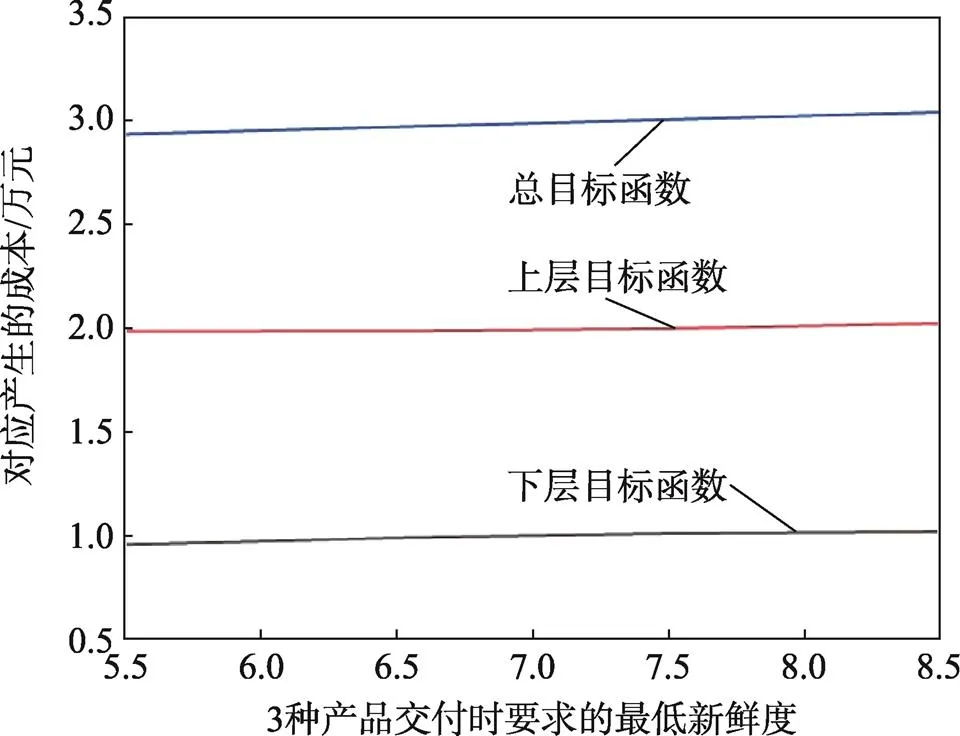
图4 成本随新鲜度的变化情况

如图4所示，随着产品交付时最低新鲜度这一变量数值的变化，上层配送中心的选址成本和下层客户配送路线的成本都呈上升趋势，从而导致总体成本增加，进一步验证了文中模型和算法的可行性和有效性。

4 结语

在传统生鲜品选址-路径问题研究的基础上，文中进行了扩展，一方面考虑了多种生鲜产品、多种车型，与现实情况更为贴近；另一方面，引入了新鲜度计算模型，并设计交付时产品的新鲜度必须满足客户的最低新鲜度要求，从而优化了传统方法的不足。

针对多种生鲜产品多种车型的选址-路径优化问题，文中构建了综合考虑客户时间窗和交付产品最低新鲜度约束的双层目标规划模型，并以物流系统总成本最小化为优化目标，其中第1阶段目标函数考虑配送中心建设成本、库存管理成本；第2阶段目标函数综合考虑了车辆固定成本、车辆运输成本、碳排放成本、车辆等待成本、车辆惩罚成本等。基于模型特点，采用两阶段启发式算法，第1阶段采用聚集度的启发式算法，将每个客户点分配给相应的配送中心，从而将多中心选址-路径模型转化成多个单中心选址-路径模型；第2阶段利用改进的蚁群算法，确定每个配送中心客户集内各点的配送顺序。

数值实验结果验证了模型的有效性和可行性，得到的主要结论包括：根据客户需求的变化，选择不同的车型进行配送，在满足客户需求的前提下，可以实现车辆固定成本和配送成本最小化，因此企业可以储备多种车型以适应客户的不同需求，在一定程度上可以降低配送成本；产品交付时最低新鲜度要求会影响配送中心的选择和车辆路径的安排，当产品交付时的新鲜度越高时，总成本也更高。由此可见，企业需要准确评估客户对产品的新鲜度要求，在一定程度可以降低物流系统的总成本。后续研究可以将生鲜产品选址-路径问题进行扩展，并结合逆向物流，综合考虑交通拥堵、天气情况对物流系统规划的影响。

[1] 杨晓芳, 姚宇, 付强. 基于新鲜度的冷链物流配送多目标优化模型[J]. 计算机应用研究, 2016, 33(4): 1050-1053.

YANG Xiao-fang, YAO Yu, FU Qiang. Multi-Objective Optimization Model of Cold Chain Logistics Distribution Based on Freshness[J]. Application Research of Computers, 2016, 33(4): 1050-1053.

[2] 陈绍洵, 兰洪杰. 基于双层规划的生鲜自提柜节点选址研究[J]. 工业工程与管理, 2018, 23(6): 57-63.

CHEN Shao-xun, LAN Hong-jie. Location of Fresh Product Self-Collection Cabinet Based on Bi-Level Programming[J]. Industrial Engineering and Management, 2018, 23(6): 57-63.

[3] 吴芳芸, 朱小林. 基于轴辐式理论的冷链物流网络优化模型[J]. 公路交通科技, 2019, 36(6): 144-150.

WU Fang-yun, ZHU Xiao-lin. Cold Chain Logistics Network Optimization Model Based on Hub-and-Spoke Theory[J]. Journal of Highway and Transportation Research and Development, 2019, 36(6): 144-150.

[4] 李善俊, 陈淮莉. 基于NSGA Ⅱ的带时间窗生鲜品配送路径优化[J]. 上海海事大学学报, 2020, 41(2): 58-64.

LI Shan-jun, CHEN Huai-li. Optimization of Fresh Food Distribution Route with Time Window Based on NSGA Ⅱ[J]. Journal of Shanghai Maritime University, 2020, 41(2): 58-64.

[5] AMORIM P, ALMADA-LOBO B. The Impact of Food Perishability Issues in the Vehicle Routing Problem[J]. Computers & Industrial Engineering, 2014, 67: 223-233.

[6] 杨霞, 范体军, 程方正. 多品种生鲜农产品的车辆路径优化[J]. 数学的实践与认识, 2019, 49(2): 198-214.

YANG Xia, FAN Ti-jun, CHENG Fang-zheng. Vehicle Routing Optimization of Multi-Variety Fresh Agricultural Products[J]. Mathematics in Practice and Theory, 2019, 49(2): 198-214.

[7] 张倩, 熊英, 何明珂, 等. 不确定需求生鲜电商配送路径规划多目标模型[J]. 系统仿真学报, 2019, 31(8): 1582-1590.

ZHANG Qian, XIONG Ying, HE Ming-ke, et al. Multi-Objective Model of Distribution Route Problem for Fresh Electricity Commerce under Uncertain Demand[J]. Journal of System Simulation, 2019, 31(8): 1582-1590.

[8] 顾莹, 杨斌. 考虑异质车辆和顾客满意度的冷藏品配送路径优化[J]. 计算机应用与软件, 2020, 37(2): 32-38.

GU Ying, YANG Bin. Route Optimization of Refrigerated Products Delivery Considering Heterogeneous Vehicles and Customer Satisfaction[J]. Computer Applications and Software, 2020, 37(2): 32-38.

[9] 陈松岩, 今井昭夫. 物流网络选址与路径优化问题的模型与启发式解法[J]. 交通运输工程学报, 2006, 6(3): 118-121.

CHEN Song-yan, IMAI Akio. Model and Heuristic Solution for Location Routing Problems of Logistics Network[J]. Journal of Traffic and Transportation Engineering, 2006, 6(3): 118-121.

[10] 石兆, 符卓. 配送选址-多车型运输路径优化问题及求解算法[J]. 计算机科学, 2015, 42(5): 245-250.

SHI Zhao, FU Zhuo. Distribution Location-Routing Problem of Heterotypic Vehicles and Its Algorithms[J]. Computer Science, 2015, 42(5): 245-250.

[11] 罗耀波, 孙延明. 基于模糊时间窗的带容积约束选址路径问题[J]. 系统工程, 2014, 32(1): 19-25.

LUO Yao-bo, SUN Yan-ming. Capacitated Location Routing Problem Based on Fuzzy Time Windows[J]. Systems Engineering, 2014, 32(1): 19-25.

[12] 杨海兰. 考虑客户价值的冷链物流多目标LRPTW问题优化研究[D]. 西安: 长安大学, 2018: 36-54.

YANG Hai-lan. Optimization of Cold Chain Logistics Multi-Objective LRPTW Problem Considering Customer Value[D]. Xi'an: Changan University, 2018: 36-54.

[13] 杨晓华, 郭健全. 模糊环境下多周期多决策生鲜闭环物流网络[J]. 计算机应用, 2019, 39(7): 2168-2174.

YANG Xiao-hua, GUO Jian-quan. Multi-Period Multi-Decision Closed-Loop Logistics Network for Fresh Products with Fuzzy Variables[J]. Journal of Computer Applications, 2019, 39(7): 2168-2174.

[14] 李冰, 党佳俊. 多配送中心下生鲜农产品同步取送选址-路径优化[J]. 智能系统学报, 2020, 15(1): 50-58.

LI Bing, DANG Jia-jun. Fresh Agricultural Cargoes Location-Routing Optimization with Simultaneous Pickup and Delivery for Multiple Distribution Centers[J]. CAAI Transactions on Intelligent Systems, 2020, 15(1): 50-58.

[15] 姬杨蓓蓓, 储昊, 成枫. 基于两阶段算法的快递企业末端配送网络优化研究[J]. 系统工程, 2019, 37(2): 100-105.

JI-YANG Bei-bei, CHU Hao, CHENG Feng. Optimization of Delivery Enterprise Delivery Network Based on Two Stage Algorithm[J]. Systems Engineering, 2019, 37(2): 100-105.

[16] 于滨, 靳鹏欢, 杨忠振. 两阶段启发式算法求解带时间窗的多中心车辆路径问题[J]. 系统工程理论与实践, 2012, 32(8): 1793-1800. YU Bin, JIN Peng-huan, YANG Zhong-zhen. Two-Stage Heuristic Algorithm for Multi-Depot Vehicle Routing Problem with Time Windows[J]. Systems Engineering-Theory & Practice, 2012, 32(8): 1793-1800.

[17] WANG Xu-ping, LI Xin-yu. Carbon Reduction in the Location Routing Problem with Heterogeneous Fleet, Simultaneous Pickup-Delivery and Time Windows[J]. Procedia Computer Science, 2017, 112: 1131-1140.

[18] 赵燕伟, 钱振宇, 张景玲, 等. 考虑碳排放的选址-路径问题研究[J]. 浙江工业大学学报, 2018, 46(5): 550-557.

ZHAO Yan-wei, QIAN Zhen-yu, ZHANG Jing-ling, et al. Research on Location Routing Problem Considering Carbon Emissions[J]. Journal of Zhejiang University of Technology, 2018, 46(5): 550-557.

[19] 吴瑶, 马祖军, 郑斌. 有新鲜度限制的易腐品生产-配送协同调度[J]. 计算机应用, 2018, 38(4): 1181-1188.

WU Yao, MA Zu-jun, ZHENG Bin. Integrated Scheduling of Production and Distribution for Perishable Products with Freshness Requirements[J]. Journal of Computer Applications, 2018, 38(4): 1181-1188.

[20] 王道平, 徐展, 杨岑. 基于两阶段启发式算法的物流配送选址-路径问题研究[J]. 运筹与管理, 2017, 26(4): 70-75.

WANG Dao-ping, XU Zhan, YANG Cen. Study on Location-Routing Problem of Logistics Distribution Based on Two-Stage Heuristic Algorithm[J]. Operations Research and Management Science, 2017, 26(4): 70-75.

Location Routing Optimization of Logistics Distribution Center under Freshness Limitation

LIU Lina, JIA Pengb, GAO Benc, ZHAO Xue-tingc

(a.College of Transportation Engineering b.Collaborative Innovation Center for Transport Studies c.School of Maritime Economics and Management, Dalian Maritime University, Dalian 116026, China)

The work aims to meet the requirements of high freshness when fresh products are delivered, and realize the optimization of location routing of distribution center under the scenario of multiple products and multiple vehicle models. A two-level goal programming model was constructed in view of considering the cost of carbon emission and meeting the customers' requirements for the minimum freshness of product at delivery. The optimization goal of the upper model was to minimize the fixed cost of distribution center and inventory management cost, while the optimization goal of the lower model was to minimize the fixed cost of vehicles, transportation cost, carbon emission cost and punishment cost. Combined with the characteristics of the model, a two-stage heuristic algorithm was used to solve the problem. The average cost improvement rate of the two-stage heuristic algorithm was 1.22% compared with that of genetic algorithm, and 3.03% compared with that of K-means clustering algorithm. The average improvement rate of the two-stage heuristic algorithm was 24.8% compared with that of genetic algorithm, and 33.0% compared with that of traditional K-means clustering algorithm. Through the comparative study of calculation examples, different freshness requirements have a significant impact on the location of distribution centers and the arrangement of vehicle routes. Enterprises can reduce logistics costs by means of reasonable logistics network planning and accurate evaluation of customers' requirements for product freshness.

location routing; freshness limitation; distribution center; two-level programming model

F252.14

A

1001-3563(2022)05-0232-10

10.19554/j.cnki.1001-3563.2022.05.032

2021-03-15

国家自然科学基金（72174035，71774018）；辽宁省“兴辽英才计划”（XLYC2008030）；辽宁省社会科学规划基金（L21CGL003）

刘琳（1997—），女，硕士，主要研究方向为物流系统优化设计。

贾鹏（1979—），男，博士，大连海事大学教授，主要研究方向为管理科学与工程。