发泡聚乙烯振动传递特性关系研究

宋卫生，于妞妞，薛阳，郭丹凤

发泡聚乙烯振动传递特性关系研究

宋卫生，于妞妞，薛阳，郭丹凤

（河南牧业经济学院，郑州 450046）

研究使用常用设计变量快速获取发泡聚乙烯振动传递率-频率曲线最大峰值处频率以及振动传递率的方法，降低缓冲材料测试表征工作量。首先设计等静应力实验，并通过理论分析和有限元仿真分析2种方法分别进行分析，明确变量，进而设计正交实验，在此基础上使用准牛顿法+通用全局优化法进行了公式拟合。等静应力实验结果显示，不同砝码重量与接触面积组合利用有限元仿真分析所得峰值对应频率不变，但是峰值对应传递率会发生变化。砝码重量、砝码与缓冲材料接触面积以及缓冲材料厚度作为变量分别与频率、振动传递率拟合后的2为0.996、0.951。静应力不能单独作为振动传递率-频率曲线变化的影响因素。需要选择砝码重量、砝码与缓冲材料接触面积以及缓冲材料厚度3个因素作为振动传递率-频率曲线变化影响因素。这3个因素与峰值对应的频率以及振动传递率有较为明显的潜在规律。拟合所得公式可以提高设计效率，减少缓冲材料测试的工作量。

发泡缓冲材料；振动传递特性；振动传递率；频率

冲击和振动是产品在运输过程中发生物理损伤的主要因素，冲击强度较为强烈，极易造成产品的损伤；振动强度一般较小，但是振动造成的破损属于疲劳损伤，在较长时间的振动过程中同样会造成产品的损伤。在GB/T 8166—2011《缓冲包装设计方法》[1]中，缓冲包装设计包括冲击防护设计和振动防护设计2个方面。振动传递率-频率曲线是振动防护设计的主要数据，也是国内外有关缓冲材料隔振性能研究的关键点。

巩桂芬等[2]研究了柱形空气衬垫的振动传递特性，分析初始内压和厚度对其振动传递特性的影响规律；李星占等[3]从振动响应传递率的基础概念出发，对不同输入情况下，振动响应传递率在系统零极点的特性和对系统输入的依赖性进行解析推导分析。刘林林[4]、张连文[5]等研究了水果运输包装件在不同高度的振动特性，探讨了固有频率和振动传递率峰值与堆码高度之间的关系。邢月卿[6]、刘国东[7]等研究了缓冲材料振动传递率曲线的实现方法和数据处理方法。刘乘[8]、王以华[9]等研究了利用冲击试验获得缓冲材料振动传递率的方法。上述研究主要集中在振动传递率的获取方法及其在运输包装件和缓冲材料振动特性的描述等方面。众所周知，静应力或缓冲材料厚度发生变化，缓冲材料的振动传递率-频率曲线就会变化[10-11]。在缓冲设计过程中，静应力和缓冲材料厚度是变化多样的，这就需要获取尽可能全面的振动传递率-频率曲线用于振动防护设计，工作量相对较大。为解决以上问题，文中首先研究静应力作为振动传递率-频率曲线变化因素的可行性，在此基础上，通过多项式拟合得到振动传递率及其对应频率的表达式。通过这2个表达式可以快速获取给定静应力和缓冲材料厚度条件下的振动传递率及其对应频率，降低测试工作量，提高设计效率。

1 振动传递率-频率曲线的理论推导

单自由度小阻尼线性系统稳态响应的振动传递率见式（1）[12]。

(1)

(2)

式中：为材料的弹性系数；为测试用砝码的质量。已知弹性系数与材料的弹性模量、砝码与缓冲材料接触面积以及缓冲材料厚度的关系见式（3）。

(3)

将式（3）代入式（2），并将所得固有圆频率结果代入式（1），可得振动传递率表达式的变化形式见式（4）。

(4)

式中：为外界环境的激振频率。

2 振动传递率-频率曲线的仿真分析

2.1 模型构建

有限元仿真分析所用的振动系统几何模型见图1。振动系统的有限元模型见图2。缓冲材料的网格划分尺寸为2 mm，其他部分采用默认尺寸划分网格。

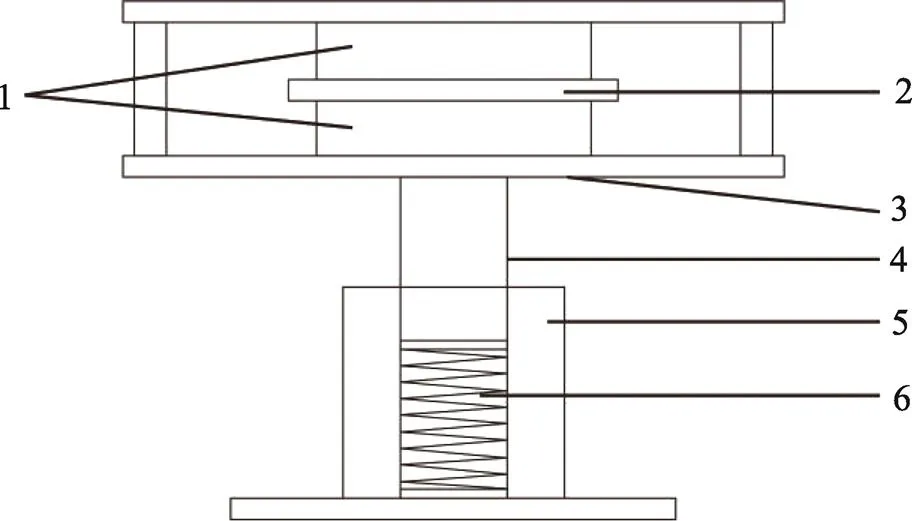
1.缓冲材料 2.砝码 3.振动台的振动台面 4.活塞 5.振动台下底座 6.振动台底部弹簧

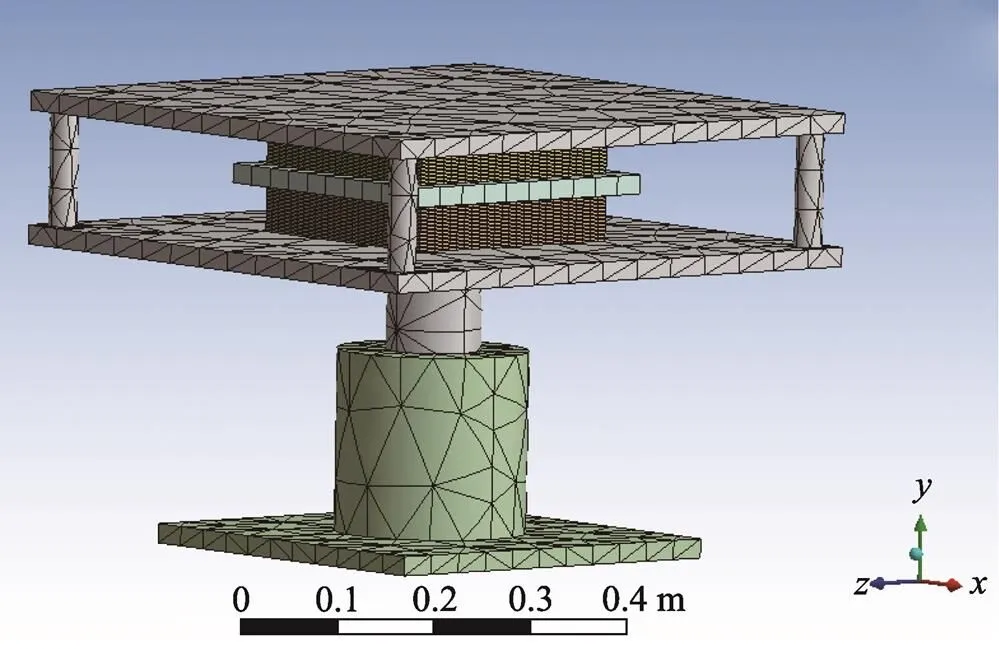
图2 振动系统有限元模型

2.2 材料参数

文中将缓冲材料、砝码、振动台主体以及弹簧的材料分别进行设置，各自的材料参数见表1[13]。

2.3 约束条件与载荷

振动系统中的接触关系设置：上、下缓冲材料与振动台台面、约束装置以及砝码的接触均有摩擦，设置为rough；振动台活塞以及下部的弹簧与底座内壁之间的接触关系设置为无摩擦；为了能够灵活设置弹簧的材料属性，振动台活塞与下部的弹簧分开建模，二者之间的接触关系为bonded。

振动台底座下面要求不能移动，因此设置为固定约束，在振动台台面上施加1000 N的简谐力，以此驱动振动台产生振动。振动过程中，考察的频率范围设置为0～500 Hz，采样频率数设置为150个。选择振动台台面与砝码的上表面作为加速度-频率的监测面[14]，然后将砝码表面所得曲线的纵坐标除以台面所得曲线的纵坐标，即可得到振动传递率-频率曲线。

3 等静应力对比实验

3.1 实验设计

资料显示[15]，静应力和厚度是振动传递率-频率曲线变化的主要影响因素，静应力是砝码重量和砝码与缓冲材料接触面积之比。同一个静应力可以是不同砝码重量和接触面积的组合。此实验主要考察这些不同组合条件所得的振动传递率-频率曲线是否相同，以此来判断静应力是否可以单独作为振动传递率-频率曲线变化的主要影响因素。文中选取了长度为200 mm、宽度为200 mm、高度为30mm的质量块模拟产品，正方形EPE缓冲衬垫的长在100～190 mm之间变化，如果质量块选择密度为7890 kg/m3的钢材质，EPE缓冲衬垫边长尺寸为150 mm，可计算得到静应力为4123.84 Pa。为了便于开展仿真实验，砝码重量的改变方法是将体积固定为0.0012 m3，改变密度来实现的。实验设计见表2。

3.2 结果分析

根据表2所提供的10组实验的参数，文中使用理论推导所得式（4）和有限元仿真2种方式得到了振动传递率-频率曲线。以上10组实验所得曲线峰值对应的振动传递率及其对应的频率见表3。实验1的振动传递率-频率曲线见图3。

由图3和表3均可以看出，理论推导所得曲线与仿真实验所得曲线有较大的差异。从图3可以看出，理论推导和仿真实验所得曲线峰值对应的振动传递率及其对应的频率差异较大，由于式（1）为单自由度小阻尼线性系统的振动传递率表达式。由于在理论分析过程中，所建模型为离散模型，而实际的包装件和有限元所建模型均为连续模型，导致理论和有限元结果存在误差。

表1 振动系统的材料参数

Tab.1 Material parameters of vibration system

表2 静应力为4123.84 Pa的参数组合

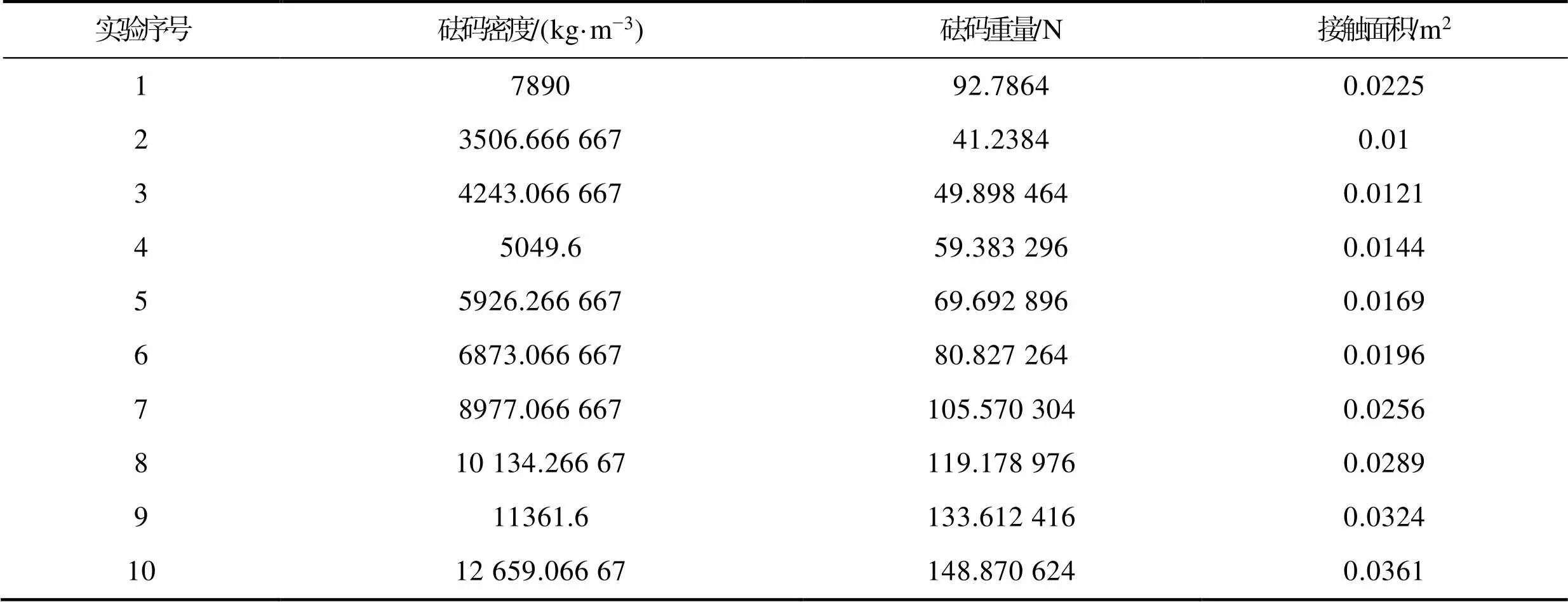
Tab.2 Parameter combination with static stress of 4123.84 Pa

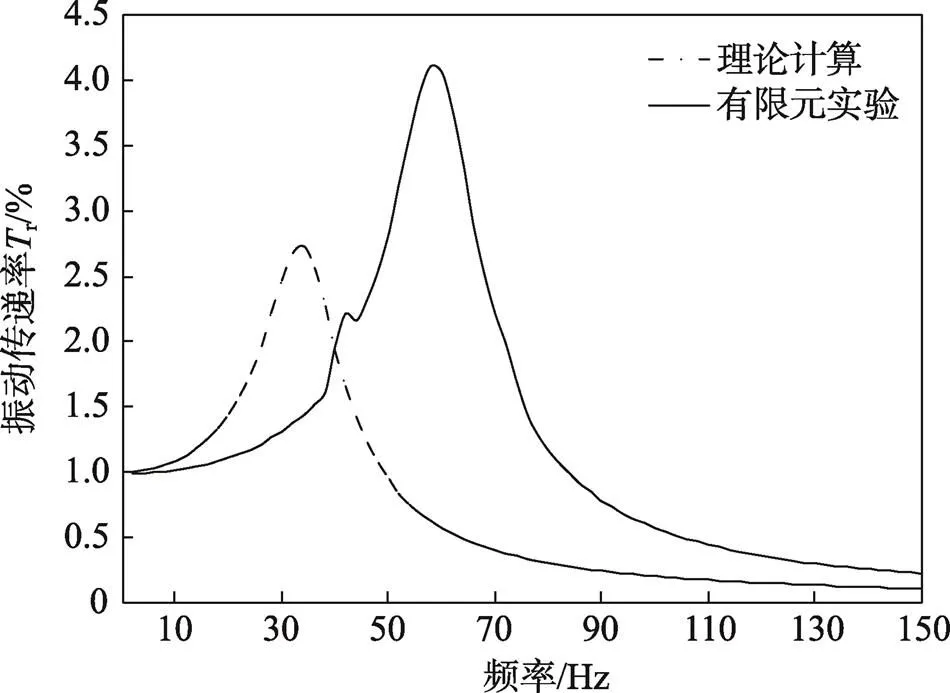
图3 实验1的振动传递率-频率曲线

由表3数据可以看出，实验1—10通过理论推导所得的频率和振动传递率均无变化，也就是说在静应力相同的情况下，不种砝码重量与接触面积组合在理论上是无差别的，静应力可以独立作为振动传递率-频率曲线变化的影响因素。通过有限元仿真方法所得结果显示，实验1—10所得峰值频率虽然没有变化，但是振动传递率却变化较大。也就是说在衰减振动没有忽略时，在静应力相同的情况下，不同砝码重量与接触面积组合是有差别的，因此静应力不能独立作为振动传递率-频率曲线变化的影响因素。

4 多重循环实验

基于等静应力实验的结果分析，选择砝码重量、砝码与缓冲材料接触面积以及缓冲材料厚度作为变量开展多重循环实验，并结合变量常用量与GB/T 8169—2008《包装用缓冲材料振动传递特性试验方法》各自设定了3个水平。多重循环实验水平表见表4，三因素三水平多重循环实验设计与实验结果见表5。

多重循环实验的方差分析结果见表6和表7。查阅F值表，并结合表6、表7可以看出，砝码重量、接触面积以及缓冲材料厚度对峰值对应频率的影响均为高度显著，而对峰值对应传递率的影响均为不显著。

表3 各实验曲线峰值对应的振动传递率和频率

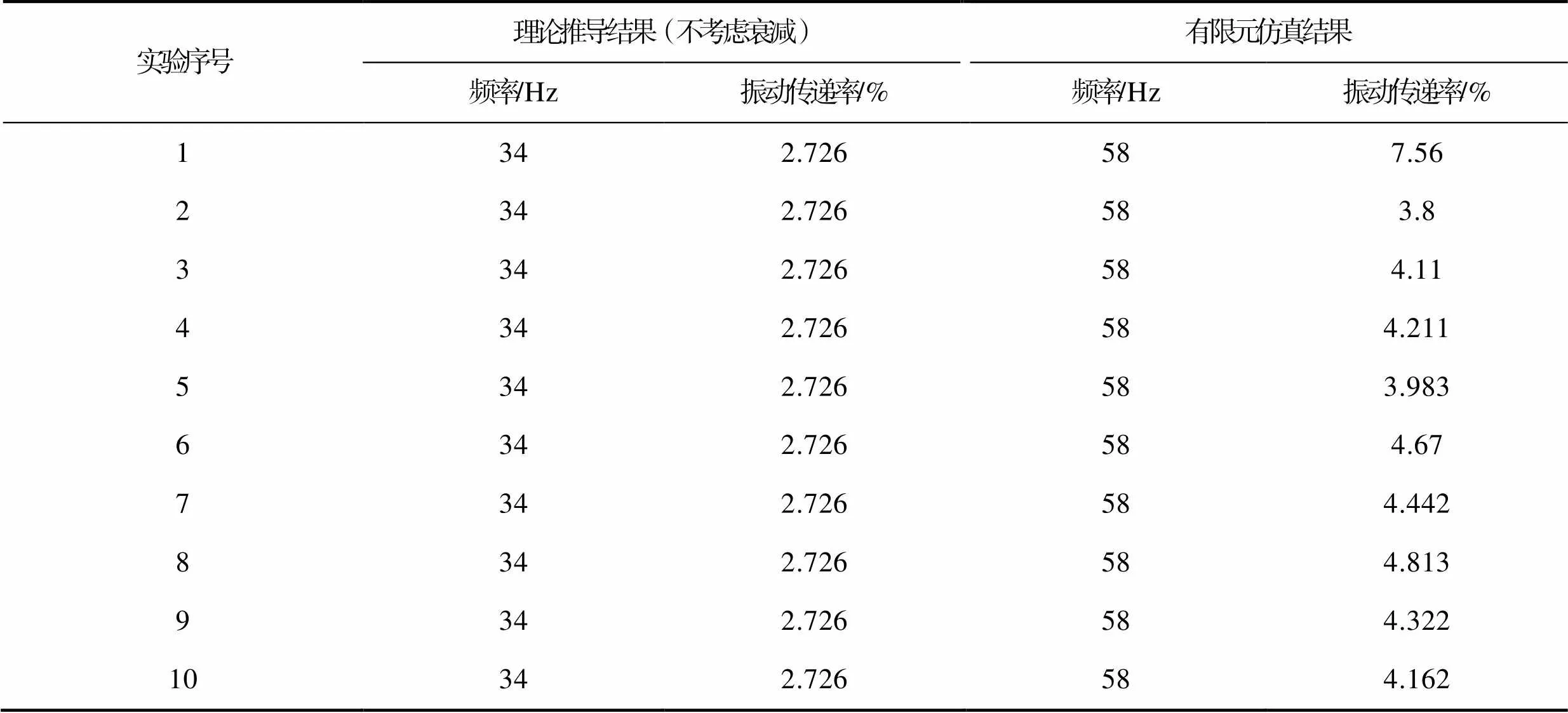
Tab.3 Vibration transmissibility and frequency corresponding to the peak value of each experimental curve

表4 多重循环实验水平

Tab.4 Multi cycle experiment levels

表5 三因素三水平多重循环实验

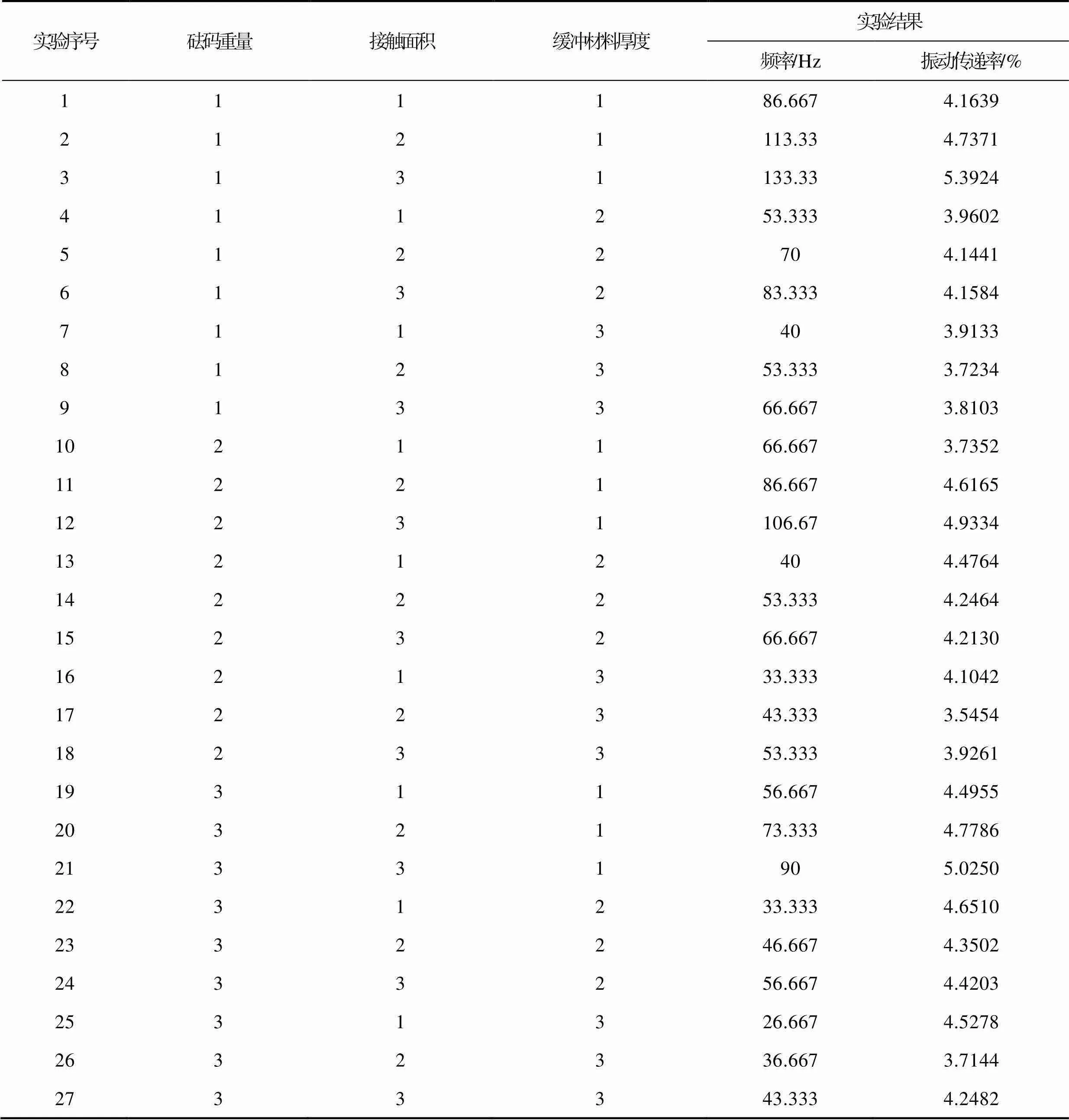
Tab.5 Three factor three level multi cycle experiment

表6 振动传递率-频率曲线峰值对应频率的多重循环实验方差分析结果

Tab.6 Results of multi cycle experiment analysis of variance of frequency corresponding to peak value of vibration transmissibility frequency curve

注：**表示该因素的影响高度显著

表7 振动传递率-频率曲线峰值对应传递率的多重循环实验方差分析结果

Tab.7 Results of multi cycle experiment analysis of variance of transmissibility corresponding to peak value of vibration transmissibility frequency curve

为了得到砝码重量、砝码与缓冲材料接触面积以及缓冲材料厚度这3个变量分别与曲线峰值对应的频率和振动传递率之间的关系，文中使用了1stOpt软件进行公式拟合。经过多个优化算法的对比，即准牛顿法(BFGS)+通用全局优化法，经过134次迭代达到收敛判断标准。相关系数之平方（2）为0.996，是所有优化算法的最高值，同时也非常接近1，说明拟合度较高。砝码重量、砝码与缓冲材料接触面积以及缓冲材料厚度与频率拟合所得关系见式（5）。

(5)

式中：为振动传递率-频率曲线峰值对应的频率；为砝码重量；为砝码与缓冲材料接触面积；为缓冲材料厚度。式中各参数识别结果见表8。

表8 式(5)中的参数识别结果

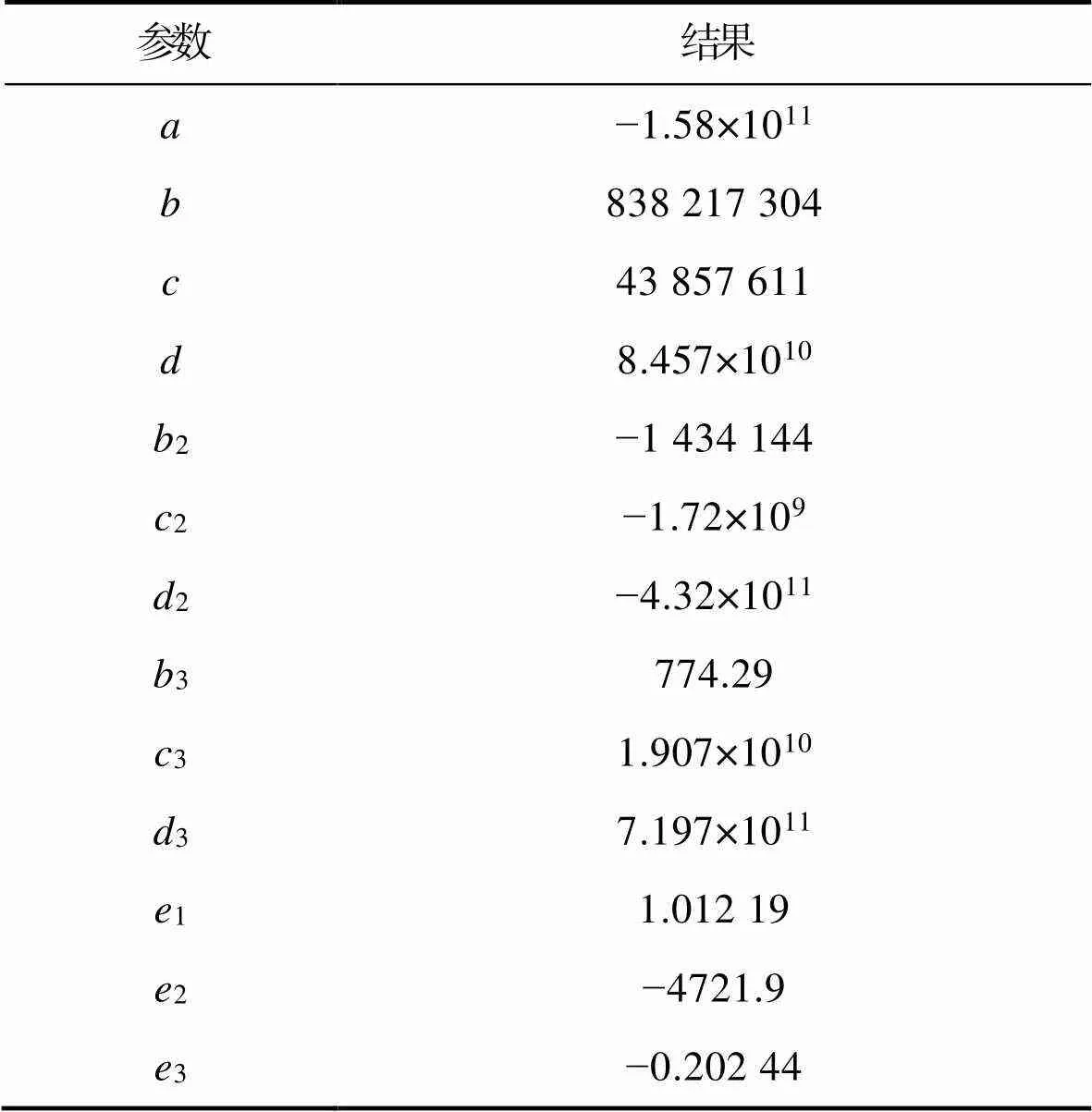
Tab.8 Parameter identification results of formula 5

使用同样的优化算法，经过22次迭代达到收敛判断标准。相关系数之平方（2）为0.951，比较接近1，拟合度也比较高。砝码重量、砝码与缓冲材料接触面积以及缓冲材料厚度与振动传递率拟合所得关系见式（6）。

(6)

式（6）中各变量的含义与式（5）相同，不再赘述，r为振动传递率，式中各参数识别结果见表9。

表9 式(6)中的参数识别结果

Tab.9 Parameter identification results of formula 6

5 结语

文中通过等静应力实验研究了静应力单独作为振动传递率-频率曲线变化影响因素的可行性，进而开展了多重循环实验。在此基础上研究了砝码重量、砝码与缓冲材料接触面积以及缓冲材料厚度这3个变量分别与曲线峰值对应的频率和振动传递率之间的关系。得到如下结论。

1）仿真实验发现振动传递率-频率曲线峰值对应的频率在等静应力条件下是不变的，但是不同砝码重量与接触面积组合所得曲线峰值对应的振动传递率是变化的，这一点与理论分析结果不同。原因在于理论分析的模型是离散模型，有限元仿真分析和实际实验的模型均为连续模型，说明在实际当中，静应力不能单独作为振动传递率-频率曲线变化影响因素。因而需要选择砝码重量、砝码与缓冲材料接触面积以及缓冲材料厚度3个因素作为振动传递率-频率曲线变化影响因素。

2）通过多重循环实验所得数据进行公式拟合，砝码重量、砝码与缓冲材料接触面积以及缓冲材料厚度3个因素分别与峰值对应的频率以及振动传递率拟合的精度均较高，说明这3个因素与峰值对应的频率以及振动传递率有较为明显的潜在规律。因而，在实际设计与测试中，产品质量已知，通过冲击防护设计可以得到产品与缓冲材料接触面积，以及缓冲材料厚度，进而可以通过文中方法较快地得到振动防护设计过程中所需要的峰值频率和振动传递率，提高设计效率，减少缓冲材料测试的工作量。

[1] GB/T 8166—2011, 缓冲包装设计方法[S].

GB/T 8166—2011, Package Cushioning Design[S].

[2] 巩桂芬, 李超. 柱形空气衬垫振动传递特性的试验研究[J]. 包装工程, 2019, 40(19): 92-96.

GONG Gui-fen, LI Chao. Experimental Study on Vibration Transmissibility Properties of Cylindrical Air Cushion[J]. Packaging Engineering, 2019, 40(19): 92-96.

[3] 李星占, 董兴建, 岳晓斌, 等. 振动响应传递率的动力学特性研究及其在工作模态分析中的应用[J]. 振动与冲击, 2019, 38(9): 62-70.

LI Xing-zhan, DONG Xing-jian, YUE Xiao-bin, et al. Dynamic Characteristics of Vibration Response Transmissibility and Its Application in Operational Modal Analysis[J]. Journal of Vibration and Shock, 2019, 38(9): 62-70.

[4] 刘林林, 呼和, 王羽, 等. 振动参数与梨损伤特性和黏弹性的关系[J]. 振动与冲击, 2016, 35(10): 139-144.

LIU Lin-lin, HU He, WANG Yu, et al. Effect of Vibration Parameters on the Damage Characteristics and Viscoelasticity of Pears[J]. Journal of Vibration and Shock, 2016, 35(10): 139-144.

[5] 张连文, 杨传民, 王勇, 等. 樱桃番茄运输包装件振动冲击性能试验[J]. 农业机械学报, 2011, 42(3): 125-130.

ZHANG Lian-wen, YANG Chuan-min, WANG Yong, et al. Vibration and Impact Performance Tests of Cherry Tomato Transport Packages[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(3): 125-130.

[6] 邢月卿, 孙德强, 方健, 等. 缓冲材料振动传递特性测试系统数据处理[J]. 包装工程, 2015, 36(15): 77-82.

XING Yue-qing, SUN De-qiang, FANG Jian, et al. Data Processing of Vibration Transmissibility Test System for Cushion Materials[J]. Packaging Engineering, 2015, 36(15): 77-82.

[7] GAY D, HOA S V. Composite Materials: Design and Applications[M]. CRC Press, 2007: 125-126.

[8] 李琛, 肖生苓, 刘颖. 热老化对聚苯乙烯缓冲材料振动传递特性的影响[J]. 科技导报, 2013, 31(35): 56-59.

LI Chen, XIAO Sheng-ling, LIU Ying. Effects of Thermal Aging on Vibration Transmissibility of Expanded Polystyrene[J]. Science & Technology Review, 2013, 31(35): 56-59.

[9] 王以华, 许锦泓, 张志良. 利用冲击试验获得缓冲材料振动传递率的方法研究[J]. 机床与液压, 2007, 35(3): 155-156.

WANG Yi-hua, XU Jin-hong, ZHANG Zhi-liang. Research on Obtaining the Vibration Transmissibility of Cushioning Materials by the Impact Test[J]. Machine Tool & Hydraulics, 2007, 35(3): 155-156.

[10] 王志伟. 运输包装[M]. 北京: 中国轻工业出版社, 2020: 66-68.

WANG Zhi-wei. Transport Packaging[M]. Beijing: China Light Industry Press, 2020: 66-68.

[11] GB/T 8169—2008, 包装用缓冲材料振动传递特性试验方法[S].

GB/T 8169—2008, Testing Method of Vibration Transmissibility for Packaging Cushioning Materials[S].

[12] 彭国勋. 物流运输包装设计[M]. 2版. 北京: 印刷工业出版社, 2012: 31.

PENG Guo-xun. Logistics Transportation Packaging Design[M]. Beijing: Cultural Development Press, 2012: 31.

[13] SASAKI H, SAITO K, ABE K. Development of an Air Cushioning Material Based on a Novel Idea[J]. Packaging Technology and Science, 1999(12): 143-150.

[14] TAKAHASHI J. Development of Environment-Friendly Cushioning Materials[J]. JPI Journal, 1997, 35(2): 166-173.

[15] 马伟伟, 钱静. 振动传递率在优化防振设计中的应用[J]. 包装与食品机械, 2008, 26(2): 42-45.

MA Wei-wei, QIAN Jing. Application of Transmissibility on Optimizing the Cushion Design[J]. Packaging and Food Machinery, 2008, 26(2): 42-45.

Relationship Between Vibration Transmissibility of Expanded Polystyrene

SONG Wei-sheng, YU Niu-niu, XUE Yang, GUO Dan-feng

(Henan University of Animal Husbandry and Economy, Zhengzhou 450046, China)

The work aims to study the frequency and vibration transmissibility at the maximum peak of the vibration transmission rate frequency curve of foamed polyethylene quickly with common design variables to reduce the workload of testing and characterization of cushioning materials.Firstly, the constant static stress experiment was designed, the results were analyzed by theoretical analysis and finite element simulation analysis, and the variables were made clear. Then the orthogonal experiment was designed, and the formula fitting was carried out by using quasi Newton method and general global optimization method. The results of constant static stress experiment showed that the peak corresponding frequency obtained by finite element simulation analysis with different weight and contact area combination remained unchanged, but the peak corresponding transmissibility would change. The R2of the weight, the contact area between the weight and the buffer material and the thickness of the buffer material fitted with the frequency and vibration transmissibility were 0.996 and 0.951 respectively.Static stress cannot be used as a single factor affecting the change of vibration transmissibility-frequency curve. It is necessary to select the weight, the contact area between the weight and the buffer material and the thickness of the buffer material as the influencing factors of the change of vibration transmissibility-frequency curve. The frequency and vibration transmissibility corresponding to the peak value have obvious potential laws with these three factors. The fitting formula can improve the design efficiency and reduce the workload of buffer material testing.

foam buffer material; vibration transmission characteristics; vibration transmissibility; frequency

TS206

A

1001-3563(2022)05-0152-07

10.19554/j.cnki.1001-3563.2022.05.021

2021-10-26

宋卫生（1980—），男，硕士，河南牧业经济学院副教授，主要研究方向为包装工程与仿真分析。