基于改进小生境粒子群的社区发现算法*
2022-03-21广东茂名幼儿师范专科学校教育技术与网络中心张金霜黄旭彬
广东茂名幼儿师范专科学校教育技术与网络中心 张金霜 黄旭彬
社区发现对增加教育虚拟社区用户粘性,提高学习者学习成效具有积极作用。为解决传统社区发现算法在复杂网络结构不清晰时划分效果不佳的问题,提出一种基于小生境的二进制粒子群优化算法NIBPSO。算法将每个粒子编码作为社区发现的一种解,以模块度作为优化函数。在粒子迭代过程中,选取粒子的邻域最优替代全局最优,同时根据粒子各维度的速度,采用轮盘赌算法确定粒子中各节点的社区归属。通过控制粒子信息传播速度和范围,能有效解决粒子陷入局部最优,提高了社区发现效果。实验表明,该算法获得较好的社区发现结果。
教育虚拟社区为学习者提供了一个开放的网络学习空间,学习者在这里交流信息、探讨问题、扩展思路、创新观念、达成共识,充分发挥集体智慧。随着人工智能和大数据技术的发展,精准教育逐步变成现实,教育虚拟社区作为精准教育的载体,在教学过程中发挥了重要作用。提升教育虚拟社区发现的效率和质量,有助于学习资源精准推送,促进学习者找到兴趣相投的学习伙伴,增加学习者对教育虚拟社区的粘性。
现实生活中,许多复杂系统都被抽象成复杂网络形式,如社交网络、论文引文网络、生物网络等。复杂网络内部可划分为多个社区,社区内部的节点联系更加紧密,而社区间关系较为稀疏。社区发现仍是目前复杂网络研究热点之一,社区划分的好坏影响社区价值的挖掘。在研究初期,有学者将社区发现理解为图分割问题、聚类问题等,提出了各种社区发现算法,比较有代表性的包括GN分裂算法、LPA标签传播算法、随机游走算法、层次聚类算法、Fast Unfolding算法等。2003年Newman等人提出模块度函数,用于评价社区划分质量,此后不少学者将社区发现问题转为目标优化问题,采用启发式算法进行研究。遗传算法、蚁群算法、蜂群算法等一系列仿生算法对于解决NP问题具有重要意义,其中粒子群优化算法就是一个典型的群仿生智能算法,对于解决这类优化问题有着较高的效率和准确性,广泛应用于社区发现。
为进一步优化社区发现质量,解决粒子群算法收敛过快,容易陷入局部最优等问题,本文提出了基于小生境的二进制粒子群算法NIBPSO。该算法结合了轮盘赌和小生境两种技术,可以有效地控制粒子的收敛速度,并保持粒子信息向下一代传递,更利于获得全局最优解。仿真结果证明,该方法相较于传统社区发现算法能获得更好的模块度值。
1 基于小生境粒子群优化算法
1.1 粒子群算法
粒子群优化算法PSO模拟鸟群觅食群体行为,将鸟群中每只鸟抽象为一个没有重量和体积的粒子,每个粒子包含一个速度矢量,该矢量确定粒子的飞行方向和距离。粒子的位置信息代表搜索空间的一个解,通过待求解问题的目标函数,评价每个粒子当前解的好坏。
PSO算法对于求解组合优化问题具有良好的效果,具有模型设计简单,控制参数较少,鲁棒性好,运行速度快等优点,但存在收敛过程容易陷入局部最优的问题,因此需要结合具体研究内容,改进算法寻优过程,综合利用PSO算法局部搜索和全局搜索能力。
基本PSO算法粒子的进化方程可描述为:
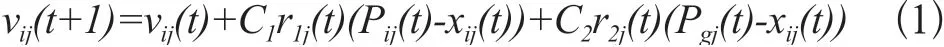

式中,x(t)是当前粒子位置;v(t)为粒子i第j维第t代的运动速度;C和C为加速度常数;r和r为[0,1]之间的随机数;P(t)是粒子个体最优位置,P(t)是粒子群的全局最优位置。从式(1)和式(2)可以看出,粒子参考个体最优和全局最优,对其速度和位置进行更新,使得粒子最终向个体最优和全局最优靠拢,以达到最优解。
1.2 目标函数
对于社区划分结果的评价,通常面临两种情况,一种是已知真实的划分结果,然后将算法发现的结果与真实结果相比较,这种情况下可采用互信息量(NMI)值进行评价;另一种更常见的情况是不确定真实的划分结果,没有任何先验知识,这种情况下需要根据各社区节点连接情况作出评价,比较著名的评价指标是模块度(Modularity)。模块度函数是一种用于评估社区划分好坏的目标函数,其基本思想是比较社区划分中,社区内部关联的稠密程度与随机网络的稠密程度。公式为:
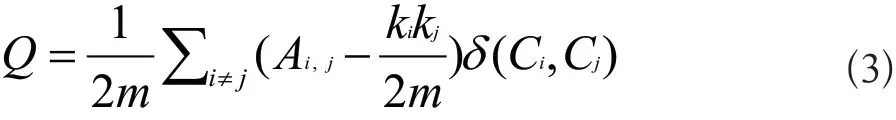
A
是整个网络对应的邻接矩阵的元素。如节点i和j有连接,则A=1
,否则A=0
;δ
(C
,C
)函数定义为如果i和j属于一个社区,即C=C
,则取值为1,否则为0;m是网络中边的总数。模块度Q取值范围在0到1之间,取值越大说明社区划分效果越好。1.3 二进制粒子群编码
标准PSO算法是针对连续优化问题而提出的,而社区发现问题的实质是确定网络各节点所属社区,即寻找一种最优节点归属组合,因此本文采用二进制粒子群算法BPSO,粒子编码采用吴朝恬提出的方案。
设网络节点数M
,若网络划分为N个社区,则粒子所需编码位置空间为M*N
。每个节点用二进制编码表示,长度为N,例如编码“010”,表示共有3个社区,且该节点归属2号社区。这种编码方式可以直观地确定每个节点所属社区,并且每个粒子代表一种社区发现结果,但缺点是需事先定义社区数量,占用空间随社区数量变化。在粒子初始化阶段,为保证解的多样性,可采用等概率轮盘赌算法随机生成粒子中各节点归属取值。
在粒子位置更新阶段,由于每次计算时,粒子各维度的结果不会正好是0或1,因此需要对结果进行修正。首先对数据进行归一化处理,然后根据归一化结果判定节点所属社区,可采用两种判定方式:一种是选择维度取值最大的对应位置,作为节点所属社区结果;另一种是继续采用轮盘赌算法,根据各维度取值的大小,决定选中该维度的概率。维度选定后,该维度对应位置编码设置为1,其他维度对应位置编码设置为0。本文采用基于速度维度概率的轮盘赌算法,这种处理方式能更大程度上保持粒子信息向下一代传递。
1.4 基于小生境的粒子群算法
小生境(Niche)是来自生物学的一个概念,指的是生物总是与自己相同的物种生活在一起,这些生物赖以生存的环境资源称为小生境。
在基本PSO算法中,粒子通过全局最优解直接作用于信息更新,在这个过程容易出现因信息传播过快,导致算法陷入局部最优。为克服这个问题,本文借用小生境思想,对粒子更新策略做如下调整:每个粒子仅与其相邻的k个粒子进行直接交互,而与其他粒子做间接交互。修改后的PSO算法进化方程如下:
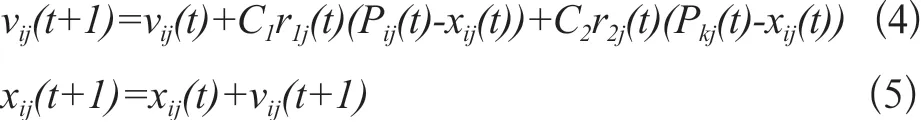
由式(4)可知,原式(1)中的P(t)被替换成了P(t),P(t)表示与粒子i相邻的k个粒子中的最优解,k值决定了小生境的范围。通过这样的机制减缓粒子信息传播的速度,有效防止粒子群算法过早收敛,同时也允许不同邻域的最优共存。随着迭代进行,粒子会向不同的区域聚集,形成各个小生境。迭代完成后,P(t)形成的群体会趋于稳定,最终得到全局最优解。
1.5 NIBPSO算法流程
NIBPSO算法求解社区发问题的流程如图1所示。
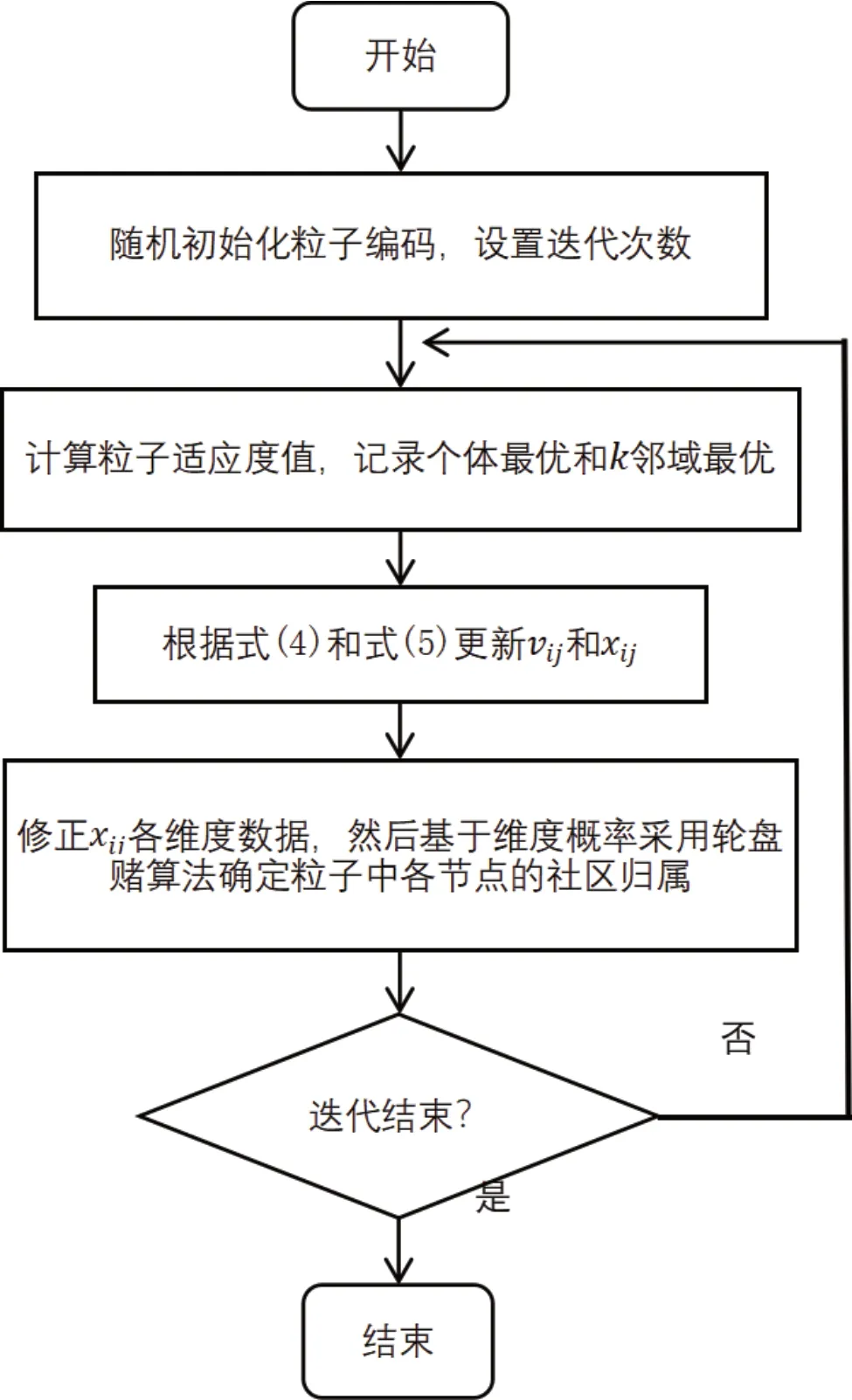
图1 NIBPSO算法流程Fig.1 NIBPSO algorithm flow
2 实验分析
2.1 实验数据集
实验采用了Karate、Dolphin、Football三组经典的网络数据集。其中Karate网络包含了34个节点和78条边,Dolphin网络包含了62个节点和159条边,Football网络包含了115个节点和616条边。
2.2 实验结果
为了验证NIBPSO算法的有效性,本文将NIBPSO算法与传统GN、LPA算法进行对比,实现非重叠社区发现,得到的模块度Q值如图2所示。
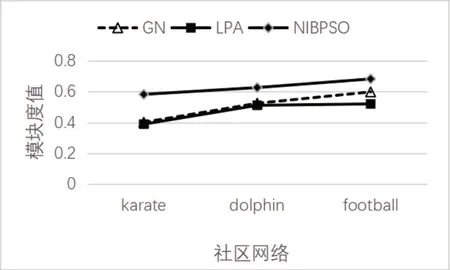
图2 各算法在3个社区网络测得的模块度值Fig.2 Modularity values measured by each algorithm in 3 community networks
由图2可以看出,基于小生境技术的粒子群NIBPSO算法相较于传统的GN、LPA算法在三个真实网络上获得更好的模块度Q值,说明该算法是有效的,在解决社区发现问题上发挥了更好的寻优作用。
3 结语
为优化社区发现,本文以模块度为目标函数,结合轮盘赌和小生境两种手段,提出一种NIBPSO优化算法。该算法无需小生境参数的先验知识,并能有效提高粒子群收敛精度。仿真实验结果表明,NIBPSO获得了更好的模块度值,社区发现效果较好。
