同轴气流式液体射流分裂液滴粒径研究1)

2022-03-20郭立梅

力学学报 2022年2期

郭立梅吕明宁智

(北京交通大学机械与电子控制工程学院,北京 100044)

引言

液体射流普遍存在于自然界和工程中.在柴油机、缸内直喷汽油机以及燃气轮机等动力机械中,燃油射流的分裂与雾化对这些动力机械的动力性、经济性以及排放特性等具有重要的影响.分裂液滴粒径的大小是液体射流雾化效果的直接体现,其对液体射流破碎具有重要影响[1-2].液滴粒径的大小往往可以反映液体射流雾化程度的好坏,所以在对液体射流雾化进行研究时,液滴粒径是非常重要的参数.因此,如何确定分裂液滴粒径一直是人们探讨的话题.

液滴的产生是由于气-液界面的扰动形成的,这种扰动以波的形式传播,在传播过程中扰动振幅不断增大,增大到一定值后射流分裂而形成液滴.目前,应用较为广泛的用于液滴粒径预测的WAVE 模型[3]即是基于上述理论进行推导得出.自19 世纪末开始[4-5],学者就对液体射流的液滴粒径开展了研究,之后的研究者也分别采用实验方法[6-10]和理论解析方法[11-22]开展了液滴粒径的预测研究.实验方法多是通过大量实验数据拟合液滴粒径表达式,而理论解析方法多是通过射流稳定性理论对液滴粒径进行研究.Teng 等[22]于1995 年提出了一种基于质量守恒定律的分裂液滴粒径计算方法,何学良和李疏松[23]通过实验对不同的液滴粒径计算公式进行了对比验证,严春吉[24]基于液滴体积守恒得到了分裂液滴粒径计算表达式.但限于影响分裂液滴粒径的因素众多,无论是实验方法还是理论解析方法,都存在一定的局限性,无法对各种类型的液体射流提出统一使用的分裂液滴粒径表达式.通过查阅相关文献[25-27],目前针对同轴气流式液体射流分裂液滴粒径的计算表达式研究较少.

基于此,本文以同轴气流式液体射流为研究对象,采用理论解析方法,建立基于临界模数的同轴气流式液体射流分裂液滴粒径表达式;在此基础上,分别研究同轴气流的旋拧作用以及气液流体的物性参数对液体射流分裂液滴粒径的影响规律,以期为同轴气流式液体射流的分裂液滴粒径预测提供参考数据.

1 同轴气流式液体射流色散方程

1.1 物理模型

本文以同轴气流式液体射流为研究对象,基于作者前期建立的物理模型[28-29]进行研究,如图1 所示.考虑一束黏性液体射流通过半径为a 的圆形喷孔喷射进入到同轴旋拧的可压缩气体介质中.将柱坐标系建立在喷嘴出口,且射流方向与z 轴方向相反.在初始阶段,射流半径为a,液体射流速度为U1;周围气体在z 轴方向速度为U2;绕z 轴旋转强度为W0,即旋转角速度与射流半径平方的乘积.

图1 物理模型Fig.1 Physical model

对上述液体射流做出如下假设:

(1) 射流周围气体为可压缩的牛顿流体;

(2) 忽略射流周围气体的黏性、重力及温度对射流的影响;

(3) 液体射流无旋转,射流周围气体作同轴旋拧运动.

1.2 色散方程

鉴于色散方程的推导过程比较复杂,且限于篇幅,本文只简要给出作者建立的基本流场、关键控制方程、边界条件以及描述同轴气流式液体射流稳定性的色散方程的最终形式,其详细的推导过程可参考文献[29].

基本流场为

可压缩旋拧气流控制方程

黏性液体射流控制方程

无量纲运动学和动力学边界条件

对控制方程进行线性扰动处理后,联立基本流场及边界条件,即可得到描述同轴气流式液体射流稳定性的色散方程的最终形式

式中,k=kr+iki,其中,kr为z 方向波数,与波长λ 的关系为kr=2πa/λ,ki为扰动空间增长率;ω=ωr+iωi,其中,ωr为扰动时间增长率(本文采用空间模式进行分析,ωr=0),ωi为波频;实数m 是角向模数,表示射流扰动在周向方向的形态,根据m数值可以将射流扰动分为轴对称扰动(m=0) 和非轴对称扰动(m ≠ 0),为韦伯数倒数;Re1=U1a/v1,为射流雷诺数;E=W0/(U1a),为无量纲旋转强度;A=U2/U1,为气液轴向速度比;Ma2=U1/c2,为气体马赫数;为气液密度比.

射流失稳以及失稳分裂后的形态由射流表面最不稳定的角向模数m 决定;将这种角向模数下的扰动称为最不稳定模态,其最大扰动增长率为各种扰动模态中之最大者;最不稳定模态所对应的角向模数称为临界模数mc.

图2 为临界模数mc为5 时的液体射流界面三维空间发展图.计算条件为:E=4,m=5,A=0,Ma2=0.6,Re1=130,Q=0.001 4,We=315.

图2 高占优模态下射流的扰动空间发展Fig.2 Disturbance spatial development of liquid jet in high critical angular modulus

如图2 所示,射流的临界模数mc=5,射流周向存在5 个“花瓣”状的扰动波;沿射流方向,当射流从喷孔喷出,无量纲长度达到5.7 时(此时射流半径r=0,结合图2 的绘图程序在计算软件Mathematica 中通过设置r=0 可以方便给出对应的无量纲长度值),射流周向的扰动波在射流中心处汇合,射流达到破碎条件开始分裂.因此,在对液滴粒径计算时应该对临界模数mc进行考虑.

2 分裂液滴粒径预测模型及讨论

2.1 基于临界模数的液滴粒径预测模型

Teng 等[22]于1995 年提出了一种基于质量守恒定律的分裂液滴粒径计算方法,该方法的基本思想是:对于直径为d0的喷孔,假设喷孔出口处速度为U0的射流在Δt 时间内生成N 个尺寸均匀的球形分裂液滴,粒径为d,并进一步假设每一个最不稳定扰动波生成一个液滴,即U0Δt=Nλ,则依据质量守恒定律可得分裂液滴粒径的计算公式为[22]

文献[13]应用实验方法测得了柴油射流分裂液滴粒径.采用文献[23]中的实验条件数据,利用Teng等[22]提出的方法进行分裂液滴粒径计算;将实验测得的液滴粒径与利用式(11)计算得到的液滴粒径进行对比,如表1 所示.

表1 分裂液滴粒径的比较Table 1 Comparison of the droplet diameter

从表1 中可以看到,利用式(11)计算得到的分裂液滴粒径明显大于文献[23]中的实验结果,说明式(11)过高估计了分裂液滴粒径.究其原因,一方面可能是由于线性理论采用了一定的假设,与实际工程条件存在诸多偏差,且实验测量的是索特平均粒径(统计平均值);另一方面则是由于该计算方法假设射流沿轴向从射流的扰动波谷处分裂,如图3(a)所示;当然,这种假设对低速射流的分裂来说是可以的.而高速射流时,临界模数一般较高,射流不仅会沿轴向从射流扰动波谷处分裂,还有可能沿径向在表面凸起的根部产生分裂,如图3(b)所示.

图3 分裂液滴形成示意图Fig.3 Schematic of splitting droplet formation

严春吉[24]提出了一种液滴粒径计算方法,认为分裂液滴体积等于一个沿轴向和径向凸起的体积.

在推导分裂液滴粒径公式时,Kim 等[14]使用了最不稳定扰动波波长的一半进行分裂液滴体积的计算,并进一步假设扰动波无量纲振幅为η=A/a 时,射流产生分裂.何学良和李疏松[23]给出的无量纲分裂液滴体积的表达式为

式中,Rd为无量纲分裂液滴半径.

式(12)将分裂液滴粒径的计算分为两种情况:射流表面临界模数为0 和大于0 的情况.临界模数为0 所对应的射流主要是低速且射流周围气体无旋的射流;对于一般燃油射流来说,临界模数大于0.

根据式(12),严春吉[24]得到无量纲分裂液滴粒径计算公式

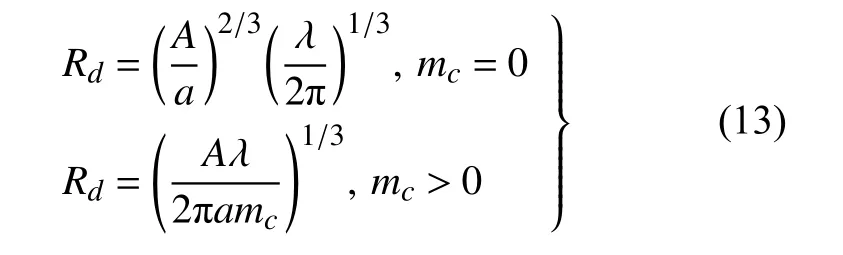
进一步假设扰动振幅A 等于未受扰液柱半径a 时射流发生分裂的条件下,得到了有量纲的射流分裂液滴粒径计算公式

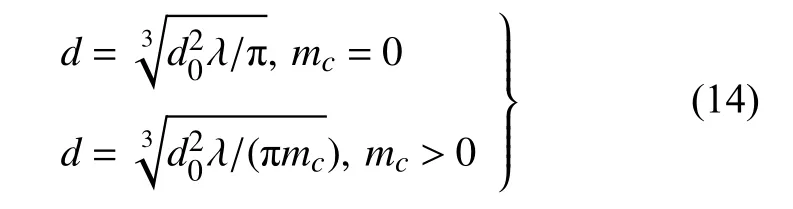
对比式(14)与式(11)可以看出,与式(11)相比,式(14)中引入了临界模数,从而可以更加准确地对高速射流的分裂液滴粒径进行预测;另外,临界模数为0 时,虽然式(14)与式(11)在形式上相似,但式中的具体内容不同.

文献[24]给出的射流分裂液滴粒径计算的基本思想比文献[22]更加合理,但文献[24]在推导射流分裂液滴粒径计算公式时,只使用了最不稳定扰动波波长的一半进行分裂液滴体积的计算.

针对文献[22]的计算方法在预测高速射流分裂液滴粒径时存在的不足以及文献[24]在推导射流分裂液滴粒径计算公式时存在的问题,本文在此基础上对分裂液滴粒径计算方法进行改进.

根据低速射流和高速射流分裂液滴形成的特点,可将分裂液滴粒径的计算分为两种情况:即射流表面临界模数mc=0 和mc≥ 1 的情况.

对于临界模数mc=0 的低速射流来说,由于射流沿轴向从射流表面扰动波谷处分裂,因此分裂液滴粒径仍可按式(11)计算.

对于临界模数mc≥ 1 的高速射流来说,假设分裂液滴的形成分为两个阶段:首先,射流沿轴向从射流表面扰动波谷处分裂,沿轴向生成一个液滴;接着,该液滴沿径向在表面凸起根部产生二次分裂,生成mc个尺寸均匀的球形液滴,即假设二次分裂的液滴个数与临界模数相等.由此,一个二次分裂液滴体积可表示为

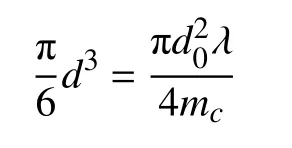
经整理,得到二次分裂液滴粒径

综合以上两种情况,改进后的分裂液滴粒径计算公式可以表示为

2.2 液滴粒径计算及验证

本文结合射流稳定性理论的分裂液滴粒径的计算步骤为:对色散方程式(10)进行数值求解,得到最大扰动增长率对应的轴向波数及临界模数;根据轴向波数与扰动波长的关系kr=πd0/λ 确定扰动波长;根据最不稳定扰动波长λ 及临界模数mc,由式(16)确定分裂液滴粒径d.

分别在两组相同的实验条件数据下,将上述分裂液滴粒径改进的计算方法以及文献[20,24]的计算方法求得的分裂液滴粒径与实验结果进行对比,如表2 所示.

表2 3 种计算结果与实验结果的比较Table 2 Comparison of three theoretical results with the experimental data

从表2 中可以看到,与利用文献[22]的计算方法得到的分裂液滴粒径相比,利用改进后的计算方法得到的分裂液滴粒径与文献[23]的实验数据更为接近.利用文献[24]的计算方法得到的分裂液滴粒径与利用改进后的计算方法得到的分裂液滴粒径都比较接近文献[23]中的实验数据.

3 同轴气流式液体射流分裂液滴粒径研究

通过分裂液滴粒径公式(16)可以看出,分裂液滴粒径主要与3 个参数相关(射流喷孔直径d0,最不稳定扰动波长λ,临界模数mc).在本研究中保持喷孔直径d0不变,λ 和mc可通过对研究物理模型建立的色散方程式(10)计算求得.考虑到本文的研究对象和射流扰动模态以及最不稳定扰动波长主要受到气动力及射流物性参数的影响,因此,接下来对液滴粒径研究是主要从两个角度出发:一是研究气流旋拧对液滴粒径的影响;二是研究流体物性对液滴粒径的影响.

3.1 气流旋拧对分裂液滴粒径的影响

本文的研究对象为同轴气流式液体射流,周围气流对射流液体的作用主要包括两个方面:一是轴向引射作用,二是周向旋转作用.利用气液轴向速度比A=U2/U1来表征气流轴向引射速度的大小,利用无量纲旋转强度E=W0/(U1a)来表征气流旋转速度的大小.

图4 给出的是不同周围气流轴向引射作用下液体射流分裂液滴粒径的大小.

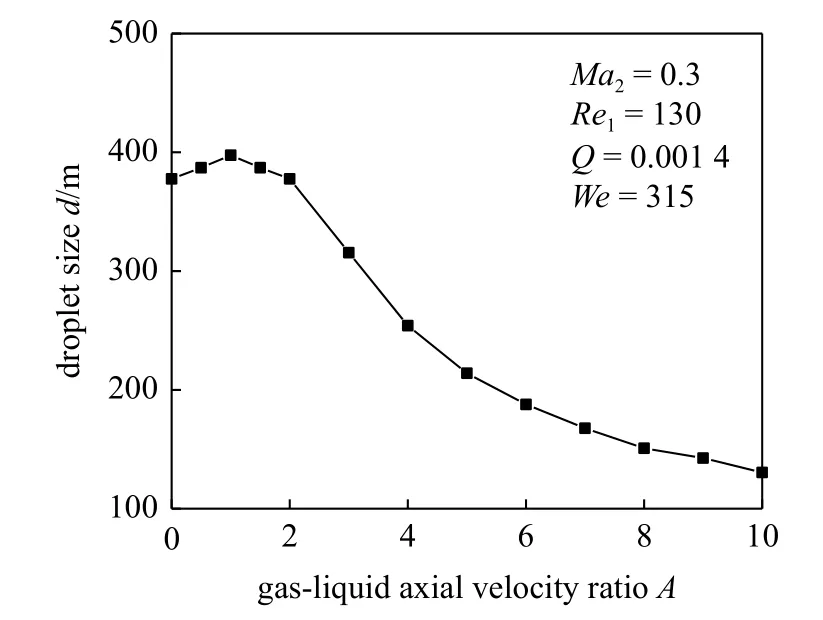
图4 不同周围气流引射速度时分裂液滴粒径Fig.4 Diameter of splitting droplet under different axial velocity of the surrounding airflow

从图4 中可以看到,液滴粒径随气液轴向速度比的增大先增大后减小,且在气液轴向速度比A ∈[0,2]内,液滴粒径关于A=1 对称.当A=1 时,液滴粒径为398 μm;当A=0 和2 时,液滴粒径均为378 μm.说明液滴粒径与气液轴向速度差有关,气液轴向速度差相等,射流失稳得到的液滴粒径是相同的.气液轴向速度比继续增大,液滴粒径减小,射流雾化效果显著增强.

图5 给出的是不同周围气流同轴旋转作用下液体射流分裂液滴粒径的大小.

图5 不同周围气流旋转速度时分裂液滴粒径Fig.5 Diameter of splitting droplet under different swirling velocity of the surrounding airflow

从图5 中可以看到,周围气流仅作同轴旋转运动时,液滴粒径随无量纲旋转强度E 的增大呈现先增大后减小的趋势.与图4 气流作轴向引射运动时不同,液滴粒径呈现一段段不连续的变化,这是由于随着周围气流旋转速度的增加,临界模数发生改变导致的.图中每组不同的点代表一种临界模数,仔细观察发现每种临界模数下的液滴粒径变化不明显,而在相邻旋转强度下临界模数改变时对应的分裂液滴粒径发生突变.从整体规律看,周围气流旋转速度较大时,分裂液滴粒径较小,射流失稳雾化效果更好.

3.2 流体物性对分裂液滴粒径的影响

结合3.1 节的研究结果并考虑到流体物性对液滴粒径的影响[30],下面将对比分析周围气流在作轴向引射作用(气流无量纲旋转强度E=0)和同轴旋转作用(气液轴向速度比A=0)时,流体物性(气体可压缩性、液体黏性、气液密度比及表面张力)对液滴粒径的影响.

3.2.1 气体可压缩性

在建立色散方程时,对气流马赫数的定义Ma2=U1/c2是以气流轴向引射流速度为基准的,尚未考虑气流的旋转速度.故本文中定义一个新无量纲数′=W0/(ac2)表征气流旋转引起的气流可压缩性的变化,Ma2′为周围气流旋转速度与声速之比.

图6 给出了不同周围气体可压缩性时液体射流的分裂液滴粒径分布.

图6 不同周围气体可压缩性时射流分裂液滴粒径Fig.6 Diameter of splitting droplet under different the compressibility of the airflow

从图6 中可以看到,周围气流仅作轴向引射运动时与周围气流仅作同轴旋转运动时,分裂液滴粒径均随气体可压缩性的增大而减小,说明气体可压缩性有利于射流雾化.但两种气流运动时气体可压缩性的作用强度不同:气流仅作轴向引射运动时,液滴粒径减小不明显,减小范围在1%左右;而从图6(b)中观察发现,周围气流作同轴旋转运动时,气体可压缩性增大后,分裂液滴粒径减小程度增大,特别是马赫数从0.3 增大到0.6 时,分裂液滴粒径显著减小,如E=2 时,液滴粒径d 从501 μm 减小至381 μm,减小幅度达到24%.

3.2.2 液体黏性

液体射流雷诺数 Re1=U1Δ f/v1,是惯性力与黏性力的比值,当保证惯性力一定时,雷诺数与运动黏度成反比例关系,可表征液体黏度大小.图7 给出了不同液体黏性时液体射流的分裂液滴粒径分布.

图7 不同液体黏度时射流分裂液滴粒径(续)Fig.7 Droplet size under different the liquid viscosity (continued)

图7 不同液体黏度时射流分裂液滴粒径Fig.7 Droplet size under different the liquid viscosity

从图7 可以看出,周围气流作轴向或周向两种运动时,液体黏度的增大均起增大分裂液滴粒径的作用,不利于射流雾化,这是因为液体黏度会抑制液体表面上扰动波的发展,并进一步抑制射流分裂成液滴,因此液体黏性力增加,分裂液滴粒径的尺寸较大.以1/Re1从0.000 4 增大到0.01 为例,气流以E=2作同轴旋转运动时液滴粒径从500 μm 增加到 511 μm,而气流以A=2 作轴向引射运动时液滴粒径从358 μm 增加到378 μm;说明相比于气流作同轴旋转运动,气流在作轴向引射运动时,受液体黏度影响较大.

3.2.3 气液密度比

从图8 中可以看到,周围气流仅作轴向引射运动与周围气流仅作同轴旋转运动时,气液密度比对分裂液滴粒径的作用效果基本一致,随着气液密度比的增加,分裂液滴的粒径减小,且影响程度大致相同,说明气液密度比的增加会在一定程度上增加射流的雾化效果.

图8 不同气液密度比时射流分裂液滴粒径Fig.8 Diameter of splitting droplet under different the gas-liquid density ratio

3.2.4 表面张力

图9 不同表面张力时射流分裂液滴粒径Fig.9 Diameter of splitting droplet under different surface tension

图9 不同表面张力时射流分裂液滴粒径(续)Fig.9 Diameter of splitting droplet under different surface tension (continued)

从图9(a)中可以看到,在1/We ∈ [0.001,0.006]研究范围内,周围气流作轴向引射运动时,分裂液滴在表面张力的作用下粒径逐渐增大,射流雾化效果变差.这是因为表面张力会克服气液之间的相互作用力来阻止液体表面的扰动或变形,进而阻碍雾化过程的进行.

从图9(b)中看到,在气流仅作同轴旋转运动时与轴向运动有同样的规律:分裂液滴粒径随表面张力的增大逐渐增大,射流雾化效果变差.不同的是E=1,1/We=0.006 时,液滴粒径发生突降,这是因为,此时表面张力的增大改变了射流的临界模数,临界模数从m=1 变为m=0,经过计算,若表面张力继续增大,液滴粒径将在d=395 μm 基础上继续增大.