光储充一体化电站优化配置方法

郭强强，皮昊书，陈云辉

(上海电力设计院有限公司，上海 200025)

目前电动汽车充电站电源单一，主要采用配电网供电形式[1-2]。电动汽车充电站内通常设有多台直流充电机。因单台直流充电机的功率较大，单次充电时间较短，这一特点导致充电站在晚间电网负荷低谷时期的利用率较低[3-4]。在日间电网负荷高峰时期，若有大量电动汽车同时需要快速充电时，大功率的充电需求将给电网产生短时负荷冲击[5]。随着电动汽车充电站建设的大范围开展，这一问题势必愈加严重[6-7]。光储充一体化电站将光伏、储能和充电站结合建设，利用电池储能系统吸收晚间负荷低谷时期的电能，对日间负荷高峰时期快充站用电进行支撑[8]，并利用光伏发电系统进行补充，能够有效平衡快充站的负荷峰谷差，提高系统运行效率，减少负荷高峰时期的电力系统资源占用，从而达到优化运行方式、提高运行经济性的目的[9-10]。

本文针对光储充一体化电站的规划需求，建立光储充一体化电站设备优化配置模型，并采用遗传算法进行求解，最后通过算例验证该方法的有效性。

1 光储充一体化电站设备模型

光储充一体化电站设备包括光伏、储能和充电桩。

1.1 光伏模型

光伏发电系统的出力受太阳辐照度、环境温度影响，因此系统的功率输出一般以标准测试条件(STC)(太阳辐照度为1 000 W/m2，温度为25℃)下的出力为标准进行修正。实际综合能源系统中，光伏发电一般运行在最大功率输出点，规划阶段可根据预测太阳辐照度或历史太阳辐照度计算其规划期内各个时段的输出功率：

(1)

式中PPV——光伏发电的输出功率；PSTC——光伏发电的额定功率；I——太阳辐照度；ISTC——STC下的太阳辐照度；T——光伏发电的运行温度；TSTC——STC下的运行温度；k——功率温度系数，为负数。

光伏发电输入为太阳能，可以看作零输入单输出元件，其输出功率的上限受自然资源的影响。光伏的功率输出约束如下：

(2)

1.2 储能模型

1.2.1 储能系统容量计算

在进行储能容量配置时，相应储能系统的充放电控制策略可以描述如下：

(3)

(4)

式中PESS_rate——储能系统额定功率，MW；SOCmax——储能电池荷电状态(SOC)上限控制值；SOCmin——储能电池SOC下限控制值。

1.2.2 考虑储能寿命模型的储能系统运行成本和效益

(1)电池储能系统的使用寿命预测模型。在计算电池储能系统运行效益时，储能系统的使用寿命是投资成本分析中最重要的一个参数。与常规机组、风机、光伏面板等相对固定的使用寿命不同，电池储能的循环次数有限，并且与其工作环境温度、充放电深度等因素密切相关，工作环境温度越高、单次充放电深度越深，其使用寿命越短。电池储能对应于额定充放电深度的有效放电电量是一定的，即充发电次数相对固定。电池储能在实际使用过程中一般限制其SOC上下限，防止其过充过放，延长电池使用寿命。对于某一实际的充放电深度可折算至有效充放电深度，拟合函数关系如下式：

(5)

式中Drate——额定放电深度；Nrate——额定放电深度对应的循环使用次数；Dr——实际使用中放电深度；Nr——实际使用中放电深度对应的循环使用次数。

若电池储能系统运行在额定放电深度下，则在其使用寿命周期内放出的总电量：

Esum=NrateDrateErate

(6)

式中Erate——电池储能的额定容量，MWh。

取Nr与Nrate的比值作为折算因子，记为mDOD，则有：

(7)

在一年计算周期内，一系列不同放电深度折算至额定放电深度下的放电电量为：

(8)

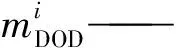
则，可得电池储能系统的使用寿命：

(9)

由式(9)可知，电池储能系统的使用寿命在实际运行过程中并非一成不变，而是与其充放电次数及每次充放电过程的深度紧密相关。

(2)储能系统的成本。储能系统的成本包括两个方面：一方面为初始投入成本，但考虑到储能系统的使用寿命，将其初始投资成本平均分摊至计算年；另一方面为运行维护成本，可按初始投资的比例计算。

则储能系统的成本计算公式如下：

(10)

式中CE——储能系统的单位容量价格，万元/MWh；Prate——储能系统的额定功率，MW；CP——储能系统的单位功率价格，万元/MW；n——储能系统的使用寿命，年；r——年利率；α——运维费用率。

2 优化配置模型

2.1 优化目标

设备模型中已经得到储能系统的收益和成本计算方法，光储充一体化电站配置的优化目标为最大化电站的净收益，如下式：

(11)

式中B——净收益；pcharge(t)——t时刻电站的充电电价；Pcharge(t)——t时刻电站的充电功率；Pele_out(t)——t时刻电站的受电电价；Pele_in(t)——t时刻电站的受电功率；Δt——计算时间间隔；pele_in(t)——t时刻电站的上网电价；Pele_out(t)——t时刻电站的上网功率；CPV——光伏的建设成本；m——光伏的使用寿命；β——光伏的运维费用率。

2.2 约束条件

在对光储充一体化电站进行配置时，模型除了满足光伏和储能系统的设备约束，还应满足系统功率平衡约束、储能系统出力约束以及储能系统SOC约束。

系统功率平衡约束：

(12)

式中SB——系统节点集合。

储能系统运行约束：

(13)

式中PESS，min(t)，PESS，max(t)——第i个储能系统在阶段t的最小和最大输出功率，与当前阶段储能系统的SOC值、SOC上下限及额定功率相关；PESS(t)——阶段t储能系统的输出功率；SOCi，max，SOCi，min——第i个储能系统SOC上下限值；SOCi(t)——阶段t储能系统的值。

3 算例分析

3.1 算例参数

本文以某光储充一体化电站为例，共配置12台60 kW快充桩，配变容量800 kVA，以1回10 kV线路接入系统。根据光储充一体化能源站屋顶面积和剩余空间，设定光伏安装容量上限为2 000 kW，储能装机容量上限为1 000 kW×2 h。

光储充一体化电站所在区域12个月典型日光伏出力如图1所示。由图1可见，光伏出力较为有规律性，在白天有光照时输出功率，夜间无输出功率。

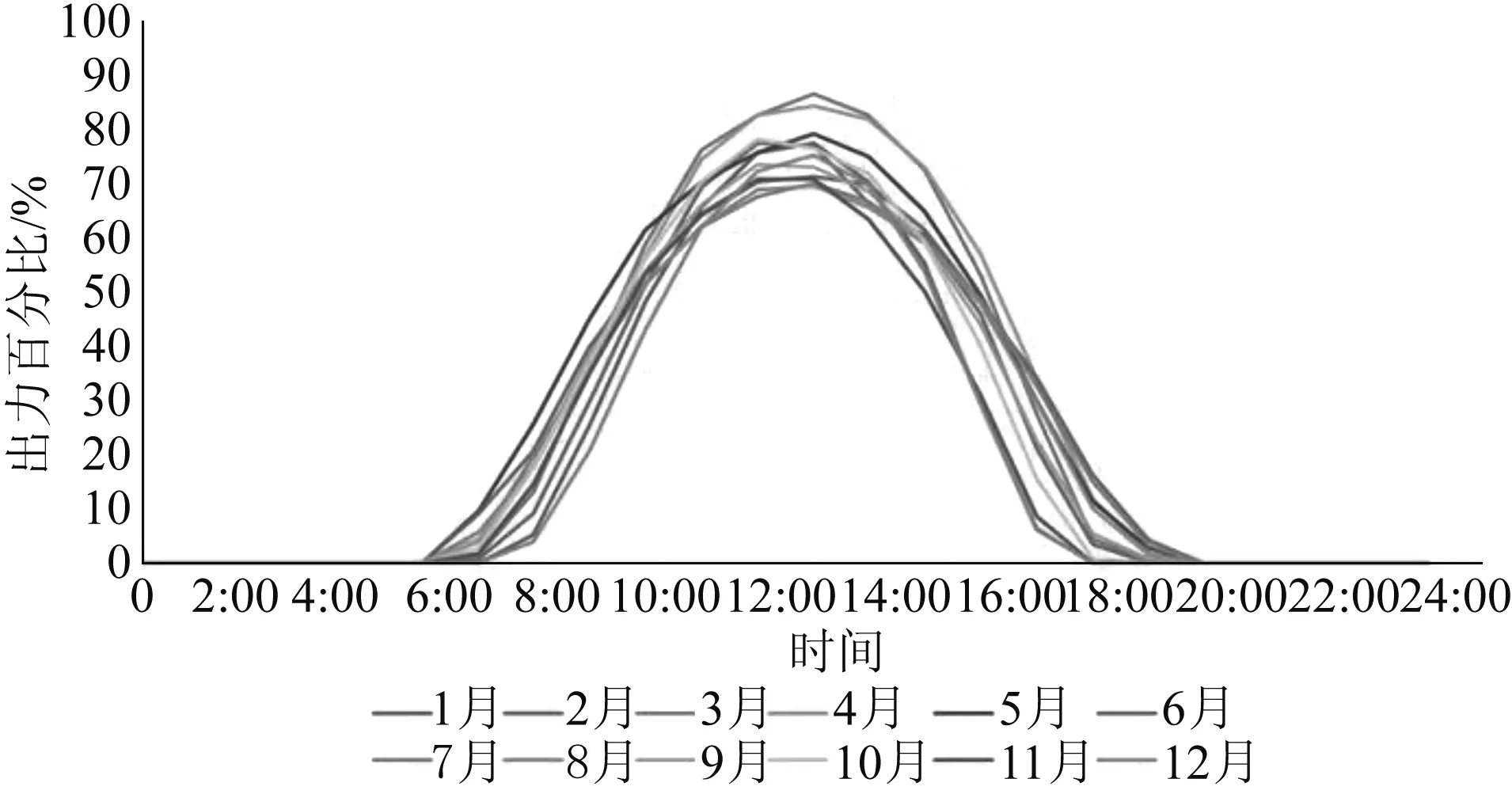
图1 12个月典型日光伏出力

充电站典型日充电负荷如图2所示。

图2 充电站典型日的充电负荷

其他计算参数见表1。

表1 计算参数表

(1)储能初期建设成本由容量成本和功率成本两部分组成，单位容量成本取600元/kWh，单位功率成本取300元/kW。

(2)储能全寿命周期的另一项成本为运行维护成本，取费用率为初期建设成本的3%。

(3)储能系统的充放电效率均取90%。

(4)储能额定放电深度下循环次数取3 000次，用于计算储能寿命。

(5)储能额定放电功率与其额定容量有关，限制在0.5～2.0 A·H，不是无限制缩小或放大其额定功率。

(6)进行优化计算时取调度周期为1 h。

电价包括受电电价、充电电价和上网电价这3个部分。受电电价为光储充一体化电站向电网买电的电价，充电电价为光储充一体化电站向电动汽车充电的电价，上网电价为光储充一体化电站向电网倒送电时电网公司的购电电价。

3.2 优化配置结果

基于计算参数，采用遗传算法进行优化求解，优化得到光伏的安装容量(峰值)为1 136 kW，储能的额定容量为564 kW×2 h，额定功率为0.5 C，最优的净收益为106.6万元。优化方案与其他方案对比见表2。

表2 光储充一体化电站配置方案对比

最优方案的净收益最高，为106.6万元，其次为方案2，净收益103.9万元，方案1的净收益最小，为82.9万元。方案1收益较低的原因在于光伏装机容量较大，考虑光储充一体化电站内部消纳后上网功率仍超过了配变的容量，需要限制光伏的出力，因此导致收益下降。

对于最优方案，光储充优化出力曲线见图3。凌晨为电价低谷，并且光伏没有出力，光储充一体化电站从电网受电为充电负荷供电及为储能充电。7:00—14:00光伏大发，超过光储充一体化电站的充电功率，向电网反送电赚取上网收益。15:00—17:00光伏出力降低，充电负荷达到高位，但此时为平时段电价，由电网为充电负荷供电。18:00—22:00为高峰电价时段，由储能放电为充电负荷供电，此时既不向电网受电也不向电网供电。

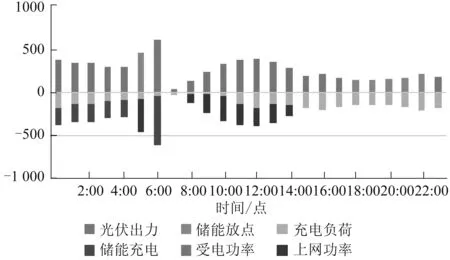
图3 光储充优化出力曲线

4 结语

结合电动汽车充电桩可利用空间建设光伏和储能，并通过控制系统协调控制光伏、储能以及充电桩，能够有效降低电动汽车大规模接入带来的充电负荷峰值压力，并为充电站运营商获取额外的收益。本文针对光储充一体化电站的规划需求，首先建立了光伏模型和基于寿命预测的储能模型，然后建立了光储充一体化电站设备优化配置模型，实现了电站运营商的收益最大化。