运载火箭推力故障下轨迹在线重规划方法*

高天域，何睿智，温长新，汤国建

(1.国防科技大学 空天科学学院空天工程系·长沙·410073；2.中国人民解放军95899部队·北京·100000)

0 引 言

近年来，随着各国运载火箭技术不断提升，运载能力不断增强，对外层空间的开发与利用也在不断深化，运载火箭需要更强的自主控制能力从而妥善处理突发故障[1]。发动机是运载火箭研制过程中的重中之重，其可靠性关乎整个飞行任务的成败，然而新技术、新材料、新理论的应用不可避免地造成其可靠性降低，据统计，运载火箭主动段动力系统故障占所发故障的60%[2]。例如日本H-2运载火箭由于一级发动机提前关机，升空后严重偏离预定轨道，导致发射任务失败，造成巨大经济损失；印度GSLV-F06运载火箭发射后，2台游动发动机点火失败，导致任务失败；同样，我国也曾发生此类事故，长征五号遥二火箭因芯一级2台发动机其中一台故障导致发射任务失败，对我国后续航天任务造成影响。随着自适应制导和轨迹在线规划技术的不断成熟，发动机非致命故障的情况下，仍能通过调整火箭飞行程序完成任务。SpaceX公司发射的Falcon 9运载火箭曾在一台发动机因故障提前关机的情况下，通过增加一二级飞行时间，将主要载荷送入预定轨道，次要载荷进入较低轨道，基本完成任务；美国德尔塔4运载火箭曾利用制导控制系统重新生成故障后的飞行轨迹，对推力下降及时进行了补偿，充分利用剩余燃料完成入轨。

针对火箭故障条件下的轨迹在线重规划和制导问题，国内外开展了一定的研究。韩业鹏[3]针对大气层外动力故障，研究了入轨点更新迭代制导方法，提高了控制系统适应故障的能力。王志祥等[4]以某型号捆绑火箭为研究对象，分析了单台发动机推力下降对火箭飞行轨迹和姿态的影响，并利用Gauss伪谱法展开仿真研究。宋征宇等[5]提出了一种在线轨迹规划策略，判断火箭不可达时自主寻找最优救援轨道。李源[6]针对二级运载火箭在不同飞行段发生不同程度的故障的轨迹规划方法以及制导方法进行了研究，为运载火箭轨迹在线规划和自适应制导技术应用提供了一定参考。H.Lee等[7]通过牛顿迭代法提升了火箭应对机构故障的能力。H.Sun[8]提出了一种基于有限微分的能够适应发动机推力故障的上升段制导方法。B.Beneditkter等[9]采用无损凸化技术和连续凸化技术相结合的方式，并在优化过程中明确考虑自由终端时间的要求，提出了一种多级运载火箭主动段凸规划方法。G.A.Dukema[10]和A.J.Calise等[11]提出了一种基于预测-校正的初值生成方法，能够处理故障后返回地面的问题。除此之外，离线设计应急轨道的方法也是提高运载火箭应对故障能力的一种选择，“挑战者”号曾应用离线设计好的应急轨道，成功在一台发动机故障后进入较低的安全轨道。A.L.Cowling[12]研究了不同时刻发动机停止工作后的中止轨迹。随着箭载计算机的计算能力不断提高，未来基于自主制导方法的新型闭环控制系统架构以及多级分层轨迹优化将成为主要的研究方向[13-15]。

针对运载火箭主动段非入轨飞行段出现推力下降的问题，本文提出了一种基于能量最优的凸优化轨迹规划方法，将原非凸问题通过线性化估算和常值假设转为凸优化问题，并通过迭代得到原问题的最优解，实现该问题下轨迹快速求解。

1 数学模型描述

1.1 坐标系定义

首先定义以下2个坐标系：1)发射惯性坐标系O-xyz，坐标原点为发射点，Ox轴在火箭发射点水平面内指向发射瞄准方向，Oy轴垂直于发射点水平指向上方，Oz轴满足右手坐标系；2)近焦点坐标系Op-xpypzp，坐标原点为地心，xp轴为地心和目标轨道近地点的连线，指向近地点，yp为xp在目标轨道平面内沿轨道方向旋转90°，zp满足右手坐标系。近焦点坐标系如图1所示。

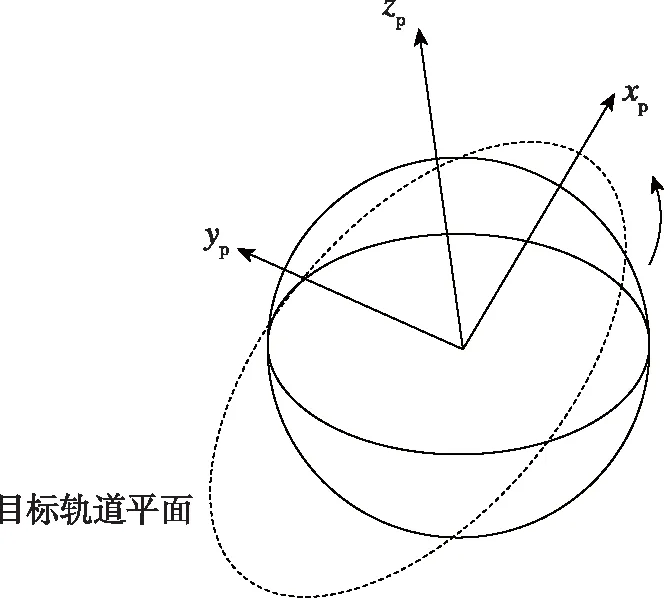
图1 近焦点坐标系Fig.1 Perifocal coordinate system

1.2 动力学模型

本文主要针对三级火箭的二级飞行段进行研究。假设故障发生于一二级分离时刻，此时火箭高度已达100km左右，大气稀薄，可忽略气动力的影响。假设地球为椭球，此时在发射惯性坐标系下建立运载火箭运动方程

(1)

式中，向量(r,v,a)分别为火箭在惯性系中的位置、速度和加速度；T为火箭在惯性系中3个方向的推力分量；Treal为运载火箭实际推力。一般情况下，火箭推力为常值，m为火箭质量，随时间变化，Isp为发动机比冲，g为引力加速度，g0为海平面重力加速度。

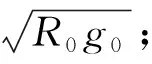
1.3 发动机推力故障模型

本文考虑的发动机推力下降模式为：由于秒耗量下降发动机推力迅速下降至某一固定值，且不考虑二次故障。表征故障的主要参数有故障发生时刻和发动机故障后输出推力的大小，以某型号芯二级4台发动机为例，各发动机发生推力下降后的数学模型为

Ti=kT(i=1,2,3,4)

(2)

其中，k为推力下降系数；Ti为故障后的推力；T为标准推力。

2 凸化算法

2.1 约束条件

2.1.1 初始状态约束

假设发动机出现故障时刻为t0，后续轨迹优化初始状态即为t0时刻火箭运动状态，X为火箭状态变量，下标0表示优化起始时刻，起始点等式约束即为

X0=[r0v0m0]

(3)

2.1.2 终端约束

由于研究对象为三级运载火箭，二级飞行段的主要任务为提升高度和速度，对终端约束并没有严格的要求，为了保证后续飞行段的稳定，增加两个终端约束。

(1)轨道面约束

为防止后续飞行出现偏离目标轨道的情况，需要将运载火箭约束在目标轨道平面内飞行。由于在发射坐标系下轨道平面相关参数计算复杂，因此将终端轨道面约束转到近焦点坐标系下，可以有效提高计算效率，轨道面约束表现形式如下

rpfz=0
vpfz=0

(4)

式中，vpfz、rpfz分别为近焦点坐标系下终端速度和高度。

近焦点坐标系和发射惯性坐标系间的转换矩阵为

(5)

式中，Ω为升交点经度；ω为近地点幅角；i为轨道倾角；λ0为发射点经度；B0为地理纬度；A0为射击方位角。

(2)终端高度约束

由于发动机秒耗量下降，火箭在燃料冗余的情况下可以适当延长二级飞行时间，火箭在三级一次飞行段过后会进入一个过渡轨道，飞行时间的延长可能导致飞行高度超过或者接近这一过渡轨道，不利于后续三级一次飞行段的轨迹规划和制导，因此在二级飞行段轨迹规划时增加飞行高度约束。以标准轨迹二级飞行结束时刻地心距作为约束边界条件。具体表现形式如下

(6)

其中，rf为故障条件下二级飞行结束时火箭的地心距；Rmax为标准轨迹二级飞行结束时火箭的地心距。

2.1.3 过程约束

当出现推力下降情况时，由于火箭推力下降，同一时刻的火箭速度、加速度和标准弹道相比也出现了下降的情况，且二级飞行段已飞出了稠密大气层，大气密度可以忽略不计。因此，与这三项相关的动压、热流、过载、弯矩等约束在同一时刻均能满足约束要求，在优化过程中不予考虑，主要考虑飞行过程中的推力约束与质量约束。

(1)推力约束

该液体火箭发动机不具备推力调节能力，其推力固定，因此视为等式约束。

(7)

(2)质量约束

为防止二级飞行段结束时出现计算错误，保证仿真符合物理规律，运载火箭在二级飞行时质量必须大于其结构质量，具体形式如下

mdry≤m(t)

(8)

其中，mdry为火箭结构质量。

2.1.4 最优化性能指标

本文所设计的最优化性能指标为终端能量最大，即飞行过程中的能量损耗最小，具体指标形式如下

(9)

其中，μ为地球引力常数；vf为终端时刻的速度。

由于终端时刻在近焦点坐标系下z方向的速度、位置分量均为0，为了简便计算，提高计算效率，将优化命题在近焦点坐标系下表示，即为

(10)

其中，rpxf、rpyf、vpxf、vpyf分别为终端时刻运载火箭在近焦点坐标系下位置和速度在x轴和y轴的分量。

2.2 最优控制问题的建立与求解

根据上述的性能指标及初始状态、终端和过程约束，以及飞行过程中的动力学约束，同时定义状态变量X=[rvm]和控制变量U=[TxTyTzTreal]，其中Tx、Ty、Tz分别为推力在近焦点坐标系下3个方向的分量。

建立如下最优控制问题Problem 1：

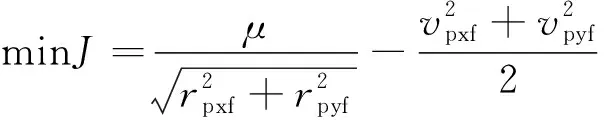
(11)

式中的非凸项主要来源有：1)性能指标为非凸函数；2)动力学方程中的引力相关项为非线性。

2.2.1 非凸项凸化处理

由于性能指标函数为非凸，因此通过线性化手段进行凸化处理，将性能指标进行一阶泰勒展开并做归一化处理，省略掉无意义的常数项和高阶项后，性能指标转化为如下形式

(12)

其中，上标0表示标准轨迹下各个相关参数。

除此之外将控制量等式约束松弛为二阶锥约束。即为

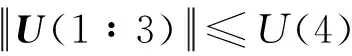
(13)

对于引力相关项，由于引力所引起的加速度与推力加速度相比为小量，同时轨迹规划的高度变化一般在几十千米以内，远小于地心距，所以对轨迹规划的影响程度并不大，因此可以基于初始轨迹进行引力加速度的快速计算。根据初始轨迹将引力相关加速度项转化为与地心距相关的线性函数，在轨迹规划过程中根据各离散点运载火箭地心距插值得到引力加速度。

gk=f(r)

(14)

其中，gk表示在离散点处的引力加速度；f(·)为引力加速度和地心距之间的关系。

由于推进剂秒耗量为常值，因此各离散点的质量mk可以直接计算

(15)

针对动力学方程，采用梯形离散法进行动力学方程的凸化，将飞行时间[t0tf]平均分为N段，离散间隔为Δt=(tf-t0)/N。具体表现形式如下

(16)

2.2.2 最优控制模型

结合上述分析，建立如下二级飞行段轨迹规划问题Problem 2：

(17)

2.2.3 求解流程

通过求解上述最优控制问题，可以得到推力故障下的最优轨迹，具体求解流程如图2所示。

1)给定离散区间N以及终端精度要求εr、εv；

2)根据运载火箭故障时间及推力故障系数计算故障后飞行时间；

(18)

其中，twork为二级工作时长；t0为发生故障时刻；tf为二级飞行段结束时刻；k为推力下降系数。

3)根据所给参数积分求解初始轨迹；

4)根据初始轨迹进行引力项的凸化；

5)应用原对偶内点法，求解问题Problem 2，得到最优解X*=[r*v*m*]，U*；

3 仿真验证与结果分析

3.1 仿真条件设置

为了充分验证本文推力故障下运载火箭非入轨段轨迹规划算法的正确性和收敛性，重点针对运载火箭二级飞行段发生故障的情况进行仿真验证。假设发生故障时刻的火箭位置速度参数均可根据导航系统或地面基站获得。

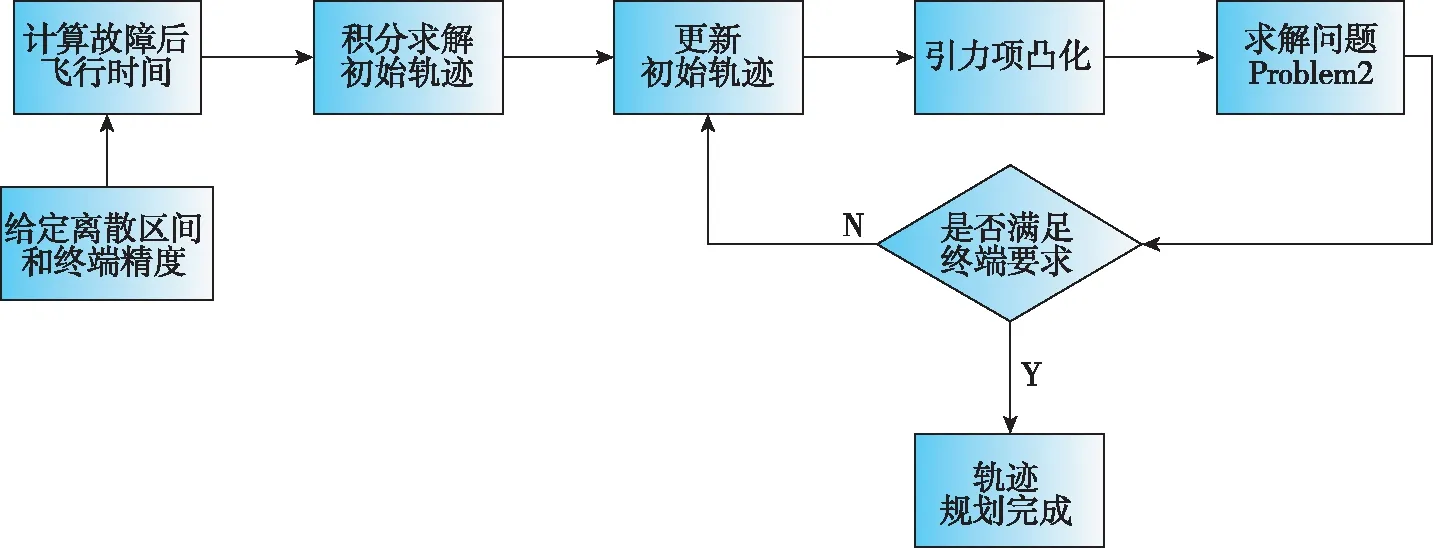
图2 求解流程Fig.2 Solving process

本文使用的仿真实验软硬件条件为Inter Corel i5-2300 CPU，3.10GHz，操作系统为Windows 7，求解轨迹规划过程中的二阶锥规划问题。

仿真过程中的无故障下运载火箭参数设置如表1所示。

表1 初始任务参数

由于研究目标为三级运载火箭，在三级一次飞行段过后运载火箭会进入一个轨道滑行，三级一次飞行段进入的目标轨道参数如表2所示。

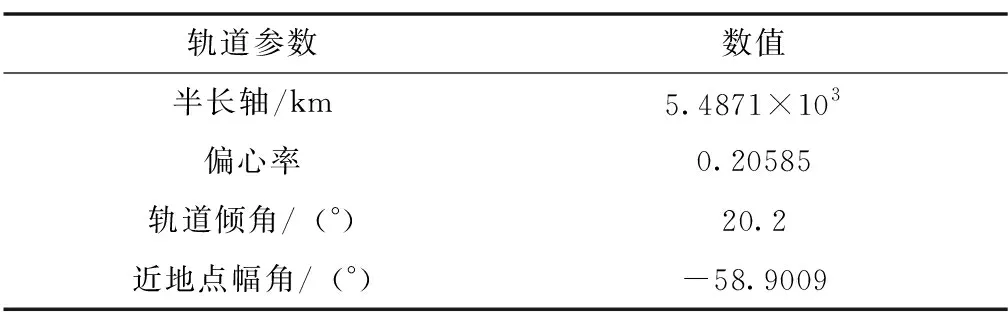
表2 目标轨道参数

发射场选为海南文昌卫星发射中心，其相关参数如表3所示。

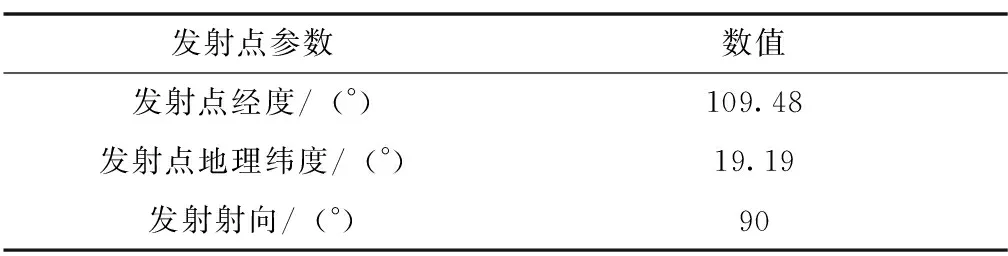
表3 发射场参数

运载火箭在整个三级飞行过程中引力和地心距的关系在发射坐标系下如图3所示，在整个优化过程中可以根据图3的关系插值得到引力加速度，从而实现引力项的凸化。

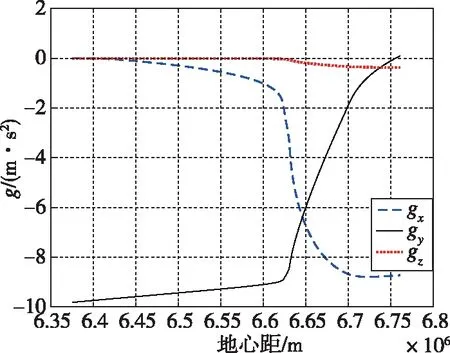
图3 引力变化曲线Fig.3 Gravitational force change curve

3.2 轨迹重规划仿真验证

针对二级点火时刻立即发生不同程度故障进行模拟，验证基于能量最优的轨迹在线重规划算法。由于二次飞行段为运载火箭的非入轨段，其主要任务为爬高和加速，因此并无严格的终端精度要求，只需速度和高度达到要求即可。能量最优性能指标可以使运载火箭充分利用所携带的燃料，以最小的能量损耗满足运载火箭终端速度和高度的约束。取离散区间N=100，εr=10-5，εv=10-5。

针对二级点火时发动机发生故障，对推力、秒耗量同时下降10%的情况进行分析，二级飞行段在线轨迹重规划仿真实验结果如图4所示。

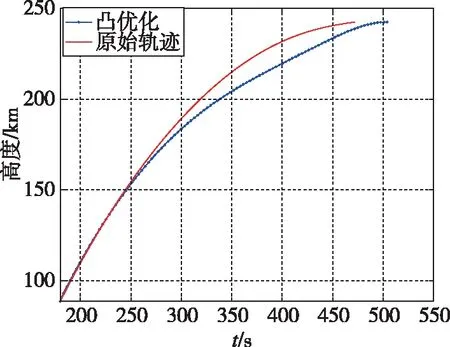
(a)高度变化曲线

具体终端误差如表4所示。

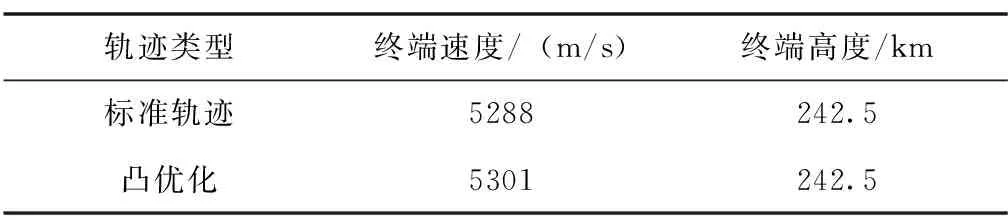
表4 终端误差对比

为验证推力经松弛后其幅值不随时间改变，推力幅值随时间的变化曲线如图5所示。

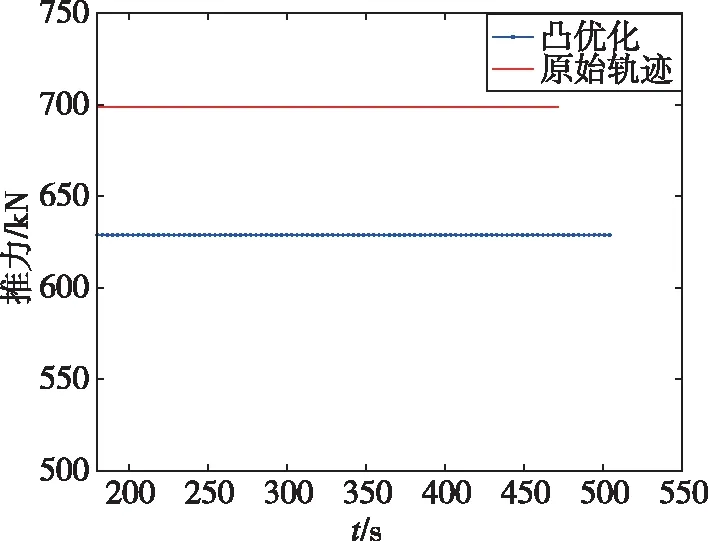
图5 推力幅值变化曲线Fig.5 Thrust amplitude variation curve

仿真结果表明，应用故障条件下基于能量最优的轨迹在线重规划算法得到的轨迹终端速度和高度误差均控制在0.2%以内，具有良好的准确度；且仅需迭代5次即可达到收敛条件，单次迭代时间在0.3s左右，具有良好的鲁棒性和稳定性。推力幅值经松弛后不随时间改变，验证了其有效性。

4 结 论

本文研究了基于能量最优的运载火箭非入轨段在发生推力故障后的轨迹重规划问题。通过无损凸化、线性化等方法，将最优控制问题转化为二阶锥规划问题后，应用原对偶内点法精确求解。仿真结果表明，该方法能够满足终端速度和高度的要求，能够完成运载火箭在该类故障下轨迹重规划，计算效率高，能够实现轨迹的快速收敛，提高了运载火箭适应故障的能力，具有在线应用的潜力。