相关寿命函数的可压缩性

0 引言

在高维列联表分析中，两个变量的关联测度在考虑第三个变量的影响有时会出现完全不同的符号，从而产生了Yule-Simpson悖论，为此需要研究关联测度的可压缩性。有许多学者研究了高维列联表中各种关联测度可压缩性的条件。如文献[1，2]找到了相对于I×J×K列联表，差积比关于背景变量可压缩的充分必要条件，文献[3]给出了2×2×K的列联表中,差积比关于有序背景变量可压缩及其强可压缩的充分必要条件。在对分的响应变量下，文献[4]给出了相对风险关于背景变量可压缩及其强可压缩的充分必要条件。文献[5]讨论了I×J×K列联表中，相对风险和差积比关于背景变量简单可压缩及其强可压缩的充分必要条件。文献[6，7]还研究了辅助交互作用、交互信息等关联测度的可压缩性条件。从文献[1][8]和[9]等的讨论可以知道，这些研究在生物医学中是十分有用的。文献[10]也从因果分析的角度给出了研究可压缩性的意义。

在生存分析中，常常用一个非负随机变量T来表示寿命，在研究实际问题时，一般要考虑系统性因素对寿命的影响。按照文献[11]的描述方式，假设X是处理(暴露)变量，Y是协变量，在一定的条件下，压缩掉协变量可能使寿命和处理之间的关系产生完全相反的结论，即出现Simpson悖论。对于寿命的一些相关函数，如生存函数、剩余寿命函数的相关测度在什么条件下可压缩呢？目前还没有发现相关的研究结果，本文打算研究寿命T关于处理(暴露)变量X、协变量Y的生存函数、剩余寿命函数等相关函数的强可压缩性、平均可压缩性问题。由于在因果分析中，可压缩性作为一个变量是否为混杂的一个标准[12]，所以找到某种变量可压缩性条件，对生存分析中影响寿命的混杂因子的辨别有重要的作用。

本文第一节给出了要研究的生存函数、剩余寿命函数、危险率函数、平均寿命、平均剩余寿命和它们的条件相依度等概念和记号，也给出了它们这些关联测度强可压缩性、平均可压缩性的定义。第二节, 在可导与可积可交换的假设下，利用条件概率的性质，对相关条件期望结果进行比较，得到了生存函数条件相依度、剩余寿命函数条件相依度的强可压缩、平均可压缩的条件，同时也得到了平均寿命、平均剩余寿命条件相依度平均可压缩的条件，这些条件目前都没有发现有已知的结果。

1 相关寿命函数的概念与记号

为了研究方便，我们记T是寿命变量，F(t)=P(T≤t)是分布函数，称S(t)=P(T>t)为T的生存函数，R(s)=P(T>t+s|T>t)称为剩余寿命生存函数。称

为T的危险率函数。

注记1 通常寿命变量T是连续的，从而有密度函数f(t)，若f(t)是右连续的，则不难证明

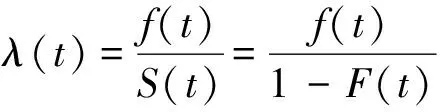
(1)

注记2 若T的生存函数S(t)可导，则不难证明

注记3 若考虑影响寿命T的处理(暴露)变量X和协变量Y，那么注记1相应函数形式也会改变，即密度函数是f(t|x,y)，生存函数是S(t|x，y),危险率函数(1)就是

从因果分析的角度来看，假设有一种处理或者暴露X对寿命T有作用，我们想要研究的是协变量Y=(Y1,Y2,…,Yp)T中哪些是因果分析中的混杂变量，它引起的混杂偏倚如何测量？这是目前因果分析没有研究的课题。

2 寿命相关函数的压缩性

按文献[14]中用条件分布的偏导数表示两个变量相依测度的思想，可以用如下的偏导数(设所需导数存在)刻画寿命T关于协变量Y各种相依测度，为了表述方便，先给出如下定义

定义1 如果所要导数存在，分别称

为T在给定X=x的条件下，关于Y=y的危险率条件相依度、生存函数条件相依度和剩余寿命生存函数条件相依度。

本节主要讨论这些条件相依度的强可压缩、平均可压缩性问题。关于强可压缩、平均可压缩的概念和定义在文献[5][15][16]中都已经给出了，为了节省篇幅这里不再赘述。

在此特别强调，本文总假设所涉及的求偏导数和求积分可以互换的条件是满足的。

2.1 寿命函数的强可压缩性

文献[15]定义了分布函数条件相依度的强可压缩性，由此可以获得生存函数条件相依度、剩余寿命生存函数条件相依度可压缩性的一个重要结论。

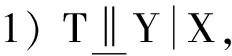
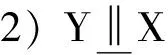
证明见文献[15]定理1，由此可以得到如下结果。

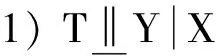
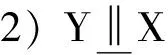
证明因为∀(t,x,y)，

S(t|x,y)=P(T>t|x,y)=1-F(t|x,y)，

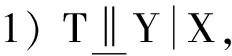
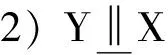
证明因为t当给定时，∀(x,y)，1-R(s|t,x,y)作为s的函数也是一个条件分布函数，事实上，按分布函数的性质逐一检验是可以证明的，从而由引理1结论成立。

2.2 寿命函数的平均可压缩性

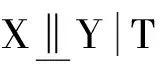
定义2 若

(2)

则称生存函数条件相依度关于Y平均可压缩。若

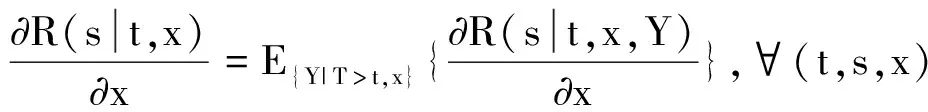
(3)

则称剩余寿命生存函数条件相依度关于Y平均可压缩。

定理3 若对任何的t，x，P(T>t|x,y)关于y是齐次的，即

∀y≠y0,P(T>t|x,y)=P(T>t|x,y0)

(4)

则生存函数条件相依度关于Y平均可压缩，即(2)式成立。

证明因为∀(t,x)，

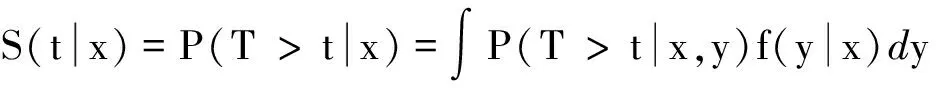
所以

(5)

由齐次性条件(4)，当∀y≠y0，P(T>t|x,y)=P(T>t|x,y0)时，必有

由(5)可得(2)成立。

定理4 如果

1)P(T>t+s|T>t,x,y) 对任何的t，s，x关于y是齐次的，即

∀y≠y0,P(T>t+s|T>t,x,y)=P(T>t+s|T>t,x,y0),或者

则

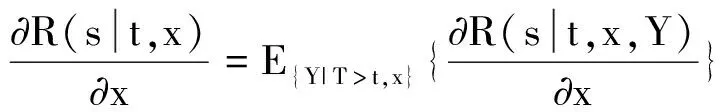
(6)

即剩余寿命生存函数条件相依度(关于Y)平均可压缩。

证明因为∀(t,s,x),

所以

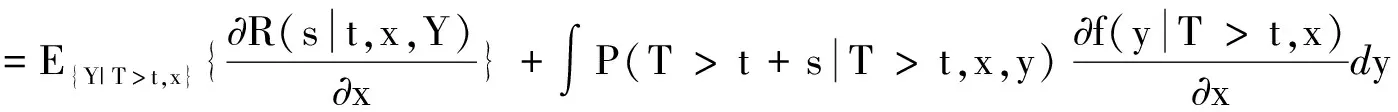
(7)

1) 在(7)式中，当P(T>t+s|T>t,x,y)对任何的t，s，x关于y是齐次的，则∀y≠y0，恒有

P(T>t+s|T>t,x,y)=P(T>t+s|T>t,x,y0)，故

=0,

由(7)式可得结论(6)成立。

2.3 寿命函数平均值的平均可压缩性

在这一小节中，我们得到了平均寿命条件相依度、平均剩余寿命条件相依度的平均可压缩性。在可靠性分析中，平均寿命、平均剩余寿命有其重要性，见文献[17]。

用E(T|x,y)表示给定X=x条件下关于y=x的总体的平均寿命，MR(t|x,y)=E(T-t|T>t,x,y)表示给定X=x条件下关于Y=y的总体的平均剩余寿命。

定义3 如果所要导数存在，分别称

为T在给定X=x条件下关于Y=y的平均寿命条件相依度和T>t之后的平均剩余寿命条件相依度。若

则称平均寿命条件相依度关于Y平均可压缩。若

则称平均剩余寿命条件相依度关于Y平均可压缩。

推论1 若对任何的t，x，P(T>t|x,y)关于y是齐次的，则平均寿命条件相依度关于Y平均可压缩。

证明由文献[17]第8页的公式(1)知道：

(8)

若对任何的t，x，P(T>t|x,y)关于y是齐次的，根据定理3，

利用积分与求导可以互换的假设，所以有

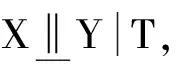
证明由于MR(t|x)=E(T-t|T>t,x)表示对任何的t≥0，寿命变量在T>t之后的期望值，

记T1=T-t，则MR(t|x)=E(T1|T1>0,x)，

利用(8)式,

其中，

S1(s|T1>0,x)=P(T1>s|T1>0,x)=P(T>t+s|T>t,x),

所以

当本推论条件成立时，利用定理4证明的(7)式同样方法可知，∀(t,x),

即平均剩余寿命条件相依度关于Y平均可压缩。

3 结论

本文研究了关于寿命变量的生存函数条件相依度和剩余寿命函数的条件相依度的强可压缩性和平均可压缩性的条件，以及平均寿命条件相依度、平均剩余寿命条件相依度的平均可压缩性条件。定理1和定理2的条件显然强于定理3、定理4，这是由于强可压缩一定严于平均可压缩。本文推论1给出了条件期望相依度平均可压缩的条件，比较文献[16]的定理1，本文的条件比它的条件要简洁，验证起来计算量明显也要小一些。

另一方面，若T|(X,Y)服从特别的分布，比如weibull分布、对数正态分布，平均可压缩性条件可否是充要条件呢？这些还需要进一步研究。