降雨入渗过程中黄土边坡失稳机理研究

李 锐， 陈 勇， 王青友

(1.朔黄铁路发展有限责任公司原平分公司，山西 忻州 036100；2.石家庄铁道大学土木工程学院，河北 石家庄 050043)

黄土具有多孔性、强透水性、湿陷性等特点，降雨是黄土滑坡最重要的一个诱发因素。相关学者分别采用试验、理论分析等方式进行了降雨对滑坡影响的相关研究。Wang F W等[1]比较了实际滑坡与排水剪切试验中所得超孔隙水压力的消散速率差值，进一步验证不排水剪切为滑坡实际发生时的状态；陈守义等[2]通过分析滑坡发生机理，将土的应力应变状态与降雨影响下滑坡发育过程对应起来；张腾等[3]进行了饱和土加载试验，得到了土体结构性与其应力比呈正相关关系；基于人工降雨试验，李汝成等[4]探讨了雨水入渗对混填路堤边坡稳定性的影响。以上学者都是基于理论公式或试验的方法研究雨水入渗对土体稳定性的影响，而数值模拟较为少见。近年来，FLAC3D软件在岩土工程中的应用日益广泛，然而利用FLAC3D软件进行非饱和渗流分析计算时，液体渗流过程中存在局限性，即FLAC3D在渗流分析计算过程中并没有考虑渗透系数变化，且不适用于含有负孔隙水压力的情况，即FLAC3D在渗流计算过程中，如果设置负孔隙水压力，该区域的饱和度将会强制置为1，从而使得在渗流计算过程中，无论是否饱和，边坡渗透系数为固定值，而在计算过程中因该区域饱和度强制设置为1，即认为该部分已饱和，这与非饱和渗流理论以及稳定性计算是相悖的。

为了解决FLAC3D软件非饱和渗流问题，国内外学者采用不同的方法对FLAC3D 的非饱和渗流计算方法进行了改进[5]，部分科技人员采用其他软件进行非饱和渗流分析，然后将渗流结果导入FLAC3D进行应力计算，对FLAC3D进行二次开发。2014年蒋中明、熊小虎等[6]提出了FLAC3D非饱和渗流分析模块的二次开发，本文将按照此思路用非饱和理论知识通过FISH语言完成非饱和渗流的二次开发，完成对实际工程数值模拟过程，并通过试验验证结论的正确性。

1 工程概况

朔黄铁路K3+0—400 m段位于山西省忻州市神池县，年均降水量达800 mm，该路段地下水水位较深，对边坡影响很小，铁路两侧均为非饱和湿陷性黄土构成的二级边坡。根据地质资料可知，坡体上层为Q3黄土，下层为Q2黄土。Q3黄土粉粒含量较大，Q2黄土空隙较多，级配较差；Q3土体密度、粘聚力、内摩擦角均小于Q2黄土。

2 基本原理与数值模型

2.1 非饱和土渗流中基本参数的关系

负孔隙水压力和含水量之间存在的函数关系可以通过分析土水特征曲线得到，考虑到土体中体积含水量θ和饱和度的关系，即θ=ns，其中n为孔隙率，s为饱和度，可以得到负孔隙水压力p和饱和度s的关系式：

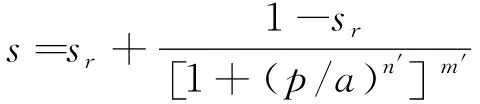
(1)

式中：sr为残余饱和度，a、m′、n′分别为拟合参数，对于一般土体a取值100，m′取值1，n′取值2。

Gardner等总结出关于渗透系数和负孔隙水压力关系式：

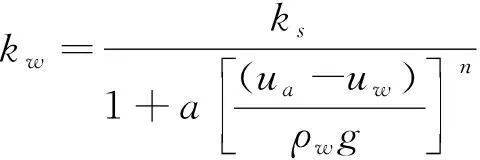
(2)

式中：kw为随负孔隙水压力变化的渗透系数；ks为土体饱和渗透系数；ua为孔隙内气压力；uw为孔隙水压力；ρw为流体密度；g为重力加速度；a和n分别为拟合参数，对于一般土体a取值0.1，n取值为2。

通过分析以上公式可以得出，土体中渗透系数随着负孔隙水压力绝对值的减小而逐渐增大，并认为渗透系数的最大值在土体饱和时达到并维持该值不变。

Fredlund等[7]提出考虑基质吸力情况下的Mohr-Coulomb公式：

τ=c′+(ua-uw)tanφb+(σ-ua)tanφ

(3)

式中：τ为抗剪强度；c′为土体有限粘聚力；φb为土体抗剪强度随着负孔隙水压力绝对值增加的坡角；σ为剪切面法向总有效应力；φ为有效内摩擦角。

2.2 FLAC3D二次开发方法

2.2.1 黄土边坡内部渗流计算

在考虑基质吸力的情况下，设置负孔隙水压力，并将对应的饱和度强制设置为1，需要通过内置z_pp(zone)来获取实时负孔隙压力值，根据公式(1)来获得实际饱和度，再根据公式(2)来获得实时渗透系数，并进行修正，利用循环函数实现每计算一步改变一次渗透系数。

2.2.2 黄土边坡稳定性计算

通过饱和度再进一步计算出含水量，最后依据负孔隙水压力值以及含水量和内摩擦角φ、粘聚力c等参数关系，利用公式(3)得出每个单元抗剪强度随降雨时间的变化值，从而得到黄土边坡位移量的大小，进而对坡体的稳定性进行分析。

2.3 数值模型的建立

为研究降雨影响下黄土边坡的失稳机理，基于二次开发后的FLAC3D软件对不同降雨强度、不同坡高、不同坡角三种情况下的边坡稳定性进行建模分析。根据现场调研及查阅资料，模型参数设置见表1。

表1 模型参数设置

依据现场实际边坡横截面建立模型：一级边坡底部长86.84 m，上部长51.8 m，高15.6 m，一级坡角41°；二级边坡下部长49.5 m，上部长30.03 m，高10.5 m，二级坡角28°。边界限制条件为顶部和斜边不采取任何位移限制措施，其余边界限制与边坡垂直方向的位移。据当地降雨资料，该研究区域降雨量可以划分为小雨(5 mm/24 h)、中雨(17 mm/24 h)、大雨(37 mm/24 h)、暴雨(75 mm/24 h)、大暴雨(175 mm/24 h)、特大暴雨(400 mm/24 h)六个等级，为了研究不同降雨强度下黄土边坡的破坏规律，选取大雨和特大暴雨两种情况进行研究。

3 不同影响因素的模拟结果分析

3.1 降雨强度对边坡稳定性的影响

图1为黄土边坡在大雨和特大暴雨强度下，负孔隙水压力随时间的变化情况。由图1可以看出，坡体表层附近负孔隙水压力变化较大，随着深度的增加，变化逐渐减小，说明降雨初期仅对表层附近有限深度影响较大。雨水入渗速率随降雨时长和深度的增加越来越慢。一级边坡坡脚位置的雨水入渗深度和负孔隙水压力变化相对最大，因此该处为整个坡面含水量最大的位置，抵抗外力的能力也最弱，最容易发生破坏。对比两种不同降雨强度下的负孔隙水压力变化情况可得：从坡面到湿润锋位置，特大暴雨强度下的负孔隙水压力值变化值要大于大雨强度，说明坡体表层含水量随降雨强度的增大而增大。随降雨时长增加，不同降雨强度下的雨水入渗深度差距不断减小，说明降雨强度对雨水入渗深度的影响很小。

图1 黄土边坡在不同降雨强度下的负孔隙水压力变化

当降雨强度为大雨时，坡体在整个降雨过程中都不会出现饱和区。在特大暴雨强度下，降雨初期，不会出现饱和区；由图1(e)可以看出，当降雨时间延长为40 h时，饱和区会出现在坡体表面；由图1(f)可以看出，降雨时间到达4 d时，饱和区域面积发生了明显扩大。这说明当降雨强度较小时，饱和区不会出现，随着降雨时长及强度的增大，当土体表面入渗流速大于土体内部湿润锋出渗流速时，饱和区将首先出现在坡体表面，并向内部扩展。

图2为小雨、大雨、特大暴雨情况下达到滑坡初始形成时截图，可以看出降雨所形成的滑坡范围随着降雨强度的增大而减小。这是因为当降雨强度较小时，雨水聚集较慢，不会产生地表径流，雨水可以被土体充分吸收，从而最大程度的弱化了土体强度，滑坡初现时间较晚但范围较大；随着降雨强度的增大，因为短时间内降水量较大，雨水在坡体表面迅速聚集，产生地表径流，土体不能吸收掉全部雨水，对深部土体的弱化作用有限，因此滑坡出现的时间较早但范围很小。

图2 不同降雨强度下的滑坡范围对比

按4种工况设置一、二级坡角，参见表2。各工况下边坡位移分布见图3。

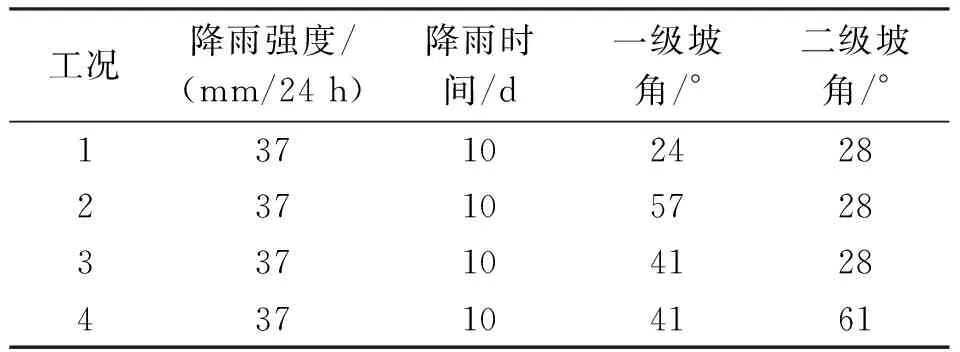
表2 边坡角度工况设置

图3 不同坡角下边坡位移分布

3.2 降雨过程中坡体角度变化对边坡稳定性的影响

由图3可以看出，随着坡角的变化，边坡位移也随之改变。一级坡角为24°时，整个二级边坡几乎不发生位移，稳定性良好，坡体发生位移部位集中在一级边坡坡脚位置，仅对该坡脚附近影响较大，见图3(a)；当一级坡角增大到57°时，整个二级边坡全部发生位移，但位移量较小，最大位移集中在二级边坡坡脚处，位移发生区域已经贯穿整个一、二级边坡，见图3(b)。二级坡角为28°时，坡体发生位移部位仅出现在一级边坡表层附近，整个二级边坡除坡脚位置外几乎不发生位移，见图3(c)；当二级坡角增大为61°时，位移发生部位已经深入一级边坡内部，且整个二级边坡全部发生位移，见图3(d)。可见，无论改变一级坡角还是二级坡角，都会影响到另一级边坡的稳定性，进而对边坡整体的稳定性造成影响。随着坡角的增大，位移量随之增加，发生位移的区域也发生扩大，导致坡体的稳定性下降，破坏越容易发生。最大位移主要在一级边坡坡脚处出现，故此位置为整个坡体最容易发生破坏的位置。

利用有限差分强度折减法计算的各个边坡角度下的安全系数关系见图4。由图4可以看出，安全系数随着一、二级坡角的增大均呈现出逐渐减小的趋势，说明随着边坡角度的增加，边坡的稳定性不断下降。

图4 边坡角度与安全系数关系

随着一级坡角的增大，边坡整体的位移量不断增加，发生位移的区域也在扩大，同时安全系数不断降低；当二级坡角增大时，边坡整体发生位移的区域同样也随之扩大，安全系数也在降低，说明一、二级坡角的增大均会降低边坡整体的稳定性。当一、二级坡角增大相同的角度后，位移扩展区域随一级坡角的增加量大于二级坡角，且一级坡角对应的安全系数下降幅度也大于二级坡角，说明一级坡角对坡体稳定性具有更大影响。这是因为二级边坡相当于施加在一级边坡上的荷载，随着一、二级坡角的增大，一级边坡比二级边坡受到更大的自重应力，更容易达到极限应力状态，所以一级坡角对整体稳定性的影响大于二级坡角。

3.3 降雨过程中坡体高度变化对边坡稳定性的影响

按4种工况设置一、二级坡高，参见表3。各工况下边坡位移分布见图5。

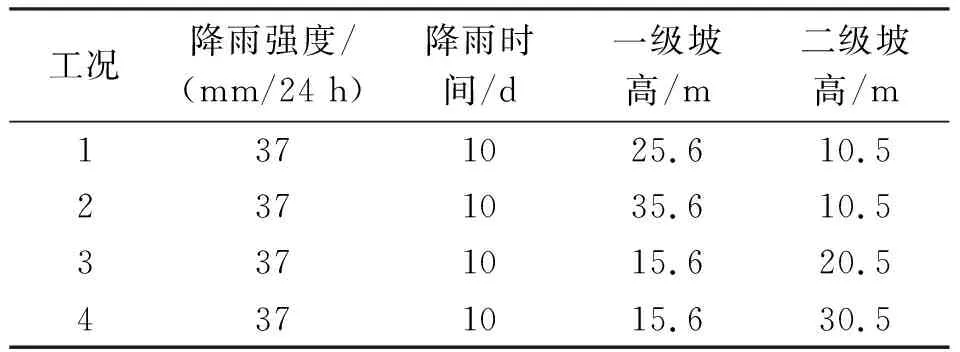
表3 边坡高度工况设置

图5 不同坡高下边坡位移分布

由图5可以看出，随着坡高的变化，边坡位移也随之改变。一级坡高为25.6 m时，位移发生区域已贯穿整个二级边坡，此时仅一级边坡内部较为稳定，坡体发生的最大位移为1.23 m，发生在一级边坡坡脚位置，见图5(a)；一级坡高为35.6 m时，一级边坡和二级边坡的位移发生区域进一步向坡体深处扩展，且位移量有所增加，一级边坡坡脚处的最大位移已经增大为1.67 m,见图5(b)。二级坡高为20.5 m时，二级边坡整体较为稳定，仅坡脚部位发生较小位移，而整个一级边坡表层坡体都发生了一定程度的位移，且一级边坡坡脚处的最大位移为1.85 m，见图5(c)；二级坡高增大为30.5 m时，二级边坡产生的位移量进一步增加，且位移发生区域已经贯通到一级边坡深处，坡体的最大位移达到1.87 m，此时坡体内部已出现不稳定状态，见图5(d)。破坏表现为从外层开始，沿整个坡面向内部层层剥落的形式，最大位移仍在一级边坡坡脚处出现，此位置为整个坡体的最危险位置。

随着一级坡高的增大，边坡整体的位移量和发生位移的区域均有所增大，稳定性下降，但对二级边坡的影响较小，这是因为一级坡高的增大仅增加了边坡整体的自重应力，而二级边坡所受荷载不变。边坡整体的位移量和发生位移的区域同样随二级坡高的增大而增大，且随着二级坡高的增大，一级边坡的位移发生区域已经从表面发展到土体内部，说明二级坡高的增大也大大降低了一级边坡的稳定性，进而促进了边坡整体的失稳。可知，无论改变一级坡高还是二级坡高，都会影响到另一级边坡的稳定性，进而对边坡整体的稳定性造成影响。对比工况1和工况3、工况2和工况4可知，在边坡总高度保持不变的情况下，随着二级坡高的增大和一级坡高的减小，边坡位移也在不断变大，且一级边坡坡脚处的最大位移分别增加了0.6 m和0.2 m，可见二级坡高对边坡整体稳定性的影响大于一级坡高。

4 黄土边坡降雨模拟试验

为验证FLAC3D软件数值模拟结果的准确性，现进行降雨模拟试验。试验室黄土边坡模型的尺寸按1∶20缩小，一级边坡底部长4.5 m、顶部长2.6 m、高0.8 m，二级边坡底部长2.5 m、顶部长1.5 m、高0.5 m；但实验室模型的一级坡角和二级坡角与实际黄土边坡保持一致，分别为41°、28°。为保证模型充分模拟黄土边坡失稳过程，土样取自山西省神池县朔黄铁路K3+0-400 m段代表性的黄土边坡，并保持扰动前黄土的密度及含水量。分别设置5组土压力传感器及孔隙压力传感器，传感器布置如图6所示。

图6 传感器布置(单位：cm)

4.1 试验过程

降雨强度选择特大暴雨，黄土边坡的破坏失稳过程如图7所示。随着降雨时间的延长，黄土边坡表面的饱和程度不断增加。未降雨时，边坡表面较为干燥；当降雨时间达到70 min时，黄土边坡表面达到较为饱和的状态，并开始出现破落掉块现象；当降雨时间延长至350 min时，坡体表面出现积水，说明此时黄土边坡表面已经完全饱和，且严重冲刷，破坏首先发生在一级边坡坡脚位置。

图7 降雨破坏试验过程

4.2 数据对比

如图8所示，随着降雨时间的延长，一级边坡坡脚处的土压力不断增加，当降雨时间超过300 min时，土压力开始下降。这是因为传感器埋置较浅，随着含水量的增加，土体的抗剪强度逐渐小于重力作用，土体发生滑落。数值模拟时较试验位置埋深较大，故最大土压力较大，但试验与数值模拟土压力值走势基本一致。

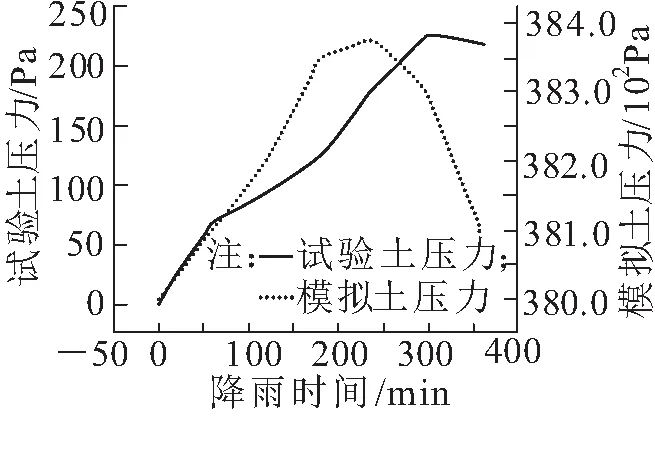
图8 土压力传感器305#数值随时间变化情况

如图9所示，随着降雨时间的延长，一级边坡坡脚处孔隙水压力首先趋于平缓，并在88 min左右开始增大，说明此时湿润峰已到达此埋置深度。试验与数值模拟的孔隙水压力值走势基本一致。

图9 孔隙水压力传感器315#数值随时间变化情况

由试验可得，黄土边坡在特大暴雨降雨强度下的破坏时间为350 min，与数值模拟的破坏时间300 min较为接近，两者的破坏时长接近，压力变化趋势基本一致，且破坏位置均发生在一级边坡坡脚处，因此可以验证数值模拟的准确性。

5 结论

(1)降雨初期，仅边坡表层范围内负孔隙水压力变化较大，随着降雨的不断进行，负孔隙水压力变化范围的增加速度越来越慢，且从表层到湿润锋位置负孔隙水压力变化逐渐减小，说明随降雨时间及深度的增加，雨水入渗能力逐渐减弱。

(2)通过对比不同强度降雨下的负孔隙水压力变化情况，得出雨水入渗深度随降雨强度的增加而增加，但增大幅度很小，随降雨时长增加，不同强度降雨入渗深度差距不断减小；降雨强度越大，从坡体表面到湿润锋位置负孔隙水压力变化值越大，说明降雨强度越大表层含水量越高；降雨强度很小时，坡体表面不会出现饱和区，当降雨时长及强度的增大到一定程度，饱和区才会出现。降雨强度越大，降雨所形成的滑坡范围越小。

(3)随着边坡角度的增大，坡体发生位移区域的面积及破坏影响范围逐渐扩大，位移也越容易发生突变。相比之下，一级坡角对坡体稳定性具有更大影响。随着边坡高度的增大，坡体最大位移随之增大，且发生位移的范围也更大，坡体越不稳定。

(4)一级边坡坡脚处，同时为整个坡体中雨水入渗深度最大位置、负孔隙水压力变化最大位置、位移最大位置，且承受较大荷载，故该处最容易发生破坏，继而上部失去支撑、贯通失稳，发生滑坡。

(5)一级边坡与二级边坡之间存在密切联系，改变其中一级边坡的坡角或坡高均会对另一级边坡的稳定性产生很大影响，两者之间的耦合作用共同决定着整个边坡的稳定性。