基于修正D-P准则的迫击炮座钣-土壤模型在强冲击载荷下的动态响应
2022-03-18王锋锋杨国来葛建立
王锋锋, 杨国来, 葛建立
(南京理工大学 机械工程学院, 南京 210094)
迫击炮是一种直接依靠座钣承受后坐力的曲射炮,具有结构简单、造价低廉等优点,在陆军作战中发挥了巨大作用。迫击炮发射时,发射载荷是强冲击载荷,弹底施加的后坐力经座钣直接作用于土壤上,靠土壤的弹性变形和塑性变形吸收后坐能量。座钣不能出现拉裂拉断现象,下沉量和形变量也不能过大,以免影响射击精度和射击稳定性[1]。然而土体的动态力学性能相当复杂,建立准确的土壤动力学模型,提高座钣-土壤耦合模型的计算精度是座钣研究的重点和难点,而动力学建模中采用的土壤屈服准则成为影响计算精度的重要因素[2]。
目前研究发现,土类材料的屈服准则应满足的基本特性主要包括拉压异性效应、正应力效应、静水应力效应、中间主应力效应、中间主剪应力效应、双剪应力正应力效应、双剪应力围压效应、应力角效应和屈服面的外凸性[3]。目前大多数应用的大型商用软件中的主要准则为Mohr-Coulomb(M-C)准则和D-P准则,它们满足的条件是不充足的。M-C准则只能满足部分条件,D-P准则不能满足应力角效应,即应力偏张量第三不变量效应,土壤的受压极限面与偏平面的交线不是圆形[4,5]。因D-P准则虽然形式简单,易于编程,且在ABAQUS软件中在设置硬化参数时可以避开黏聚力值的影响,有利于计算收敛。在迫击炮座钣计算中一般应用D-P准则,但是综合其在岩土中的应用,发现该准则应用在迫击炮座钣计算中得出的结论与实际有较大差距。因此,有必要通过修正迫击炮座钣-土壤计算模型中土壤的D-P准则来提高座钣-土壤计算模型的准确度。
李平恩等[6]提出在拉剪区修正D-P准则的两种可行性方案,第一种是在压剪区仍采用D-P准则的锥面式,而在拉剪区及其邻近,采用一个球形屈服面代替原来的锥顶附近的锥面。第二种是使用一个双曲旋转面近似地代替D-P圆锥面。Aubertin等[7-8]在研究岩土工程的应力准则时引入了一种角隅函数,周永强等[9]将这个角隅函数引入到D-P准则的修正中,研究了岩石在三轴压缩和三轴拉伸状态下不同的强度特性。周永强等[10]还结合D-P准则与次加载面理论,建立了能考虑岩石材料实际抗拉强度和应力角效应的循环加、卸载模型。此外,Alejano等[11]阐述了D-P准则的相关研究。Liu等[12]使用D-P破坏准则研究工具-岩石相互作用。 Sadoghi Yazdi等[13]将神经模糊模型与粒子群优化(PSO)结合使用,使用D-P屈服准则对线性弹性硬化塑料本构模型中使用的土壤参数进行校准。 Chen等[14]对土壤参数和采集的数据进行了测试和处理,根据基本测试对D-P土壤模型中所需的一些参数进行了测量和修改。
研究者们在D-P准则的修正和应用上做出了很大贡献,但是没有任何研究表明其在迫击炮座钣-土壤计算中的应用及效果,座钣-土壤耦合模型的计算精度也有待提高。因此,本文在综合岩土类材料D-P准则修正的基础上,首次将其应用到迫击炮座钣-土壤耦合模型计算中,设计并开展了强冲击载荷下迫击炮座钣-土壤动态响应试验,并对不同冲击载荷下修正前后座钣与土壤动态响应的数值计算值和试验测试值进行比较。结果表明,在迫击炮座钣-土壤计算中,修正土壤D-P屈服准则可以较好地描述试验现象,从而提高迫击炮座钣-土壤耦合模型的计算精度。
1 座钣-土壤受力分析与建模
1.1 迫击炮座钣-土壤受力分析
由于阵地土质的千变万化,加上炮膛合力很大,弹丸发射时座钣的受力十分复杂,图1为迫击炮在中硬土上发射时座钣的受力情况。
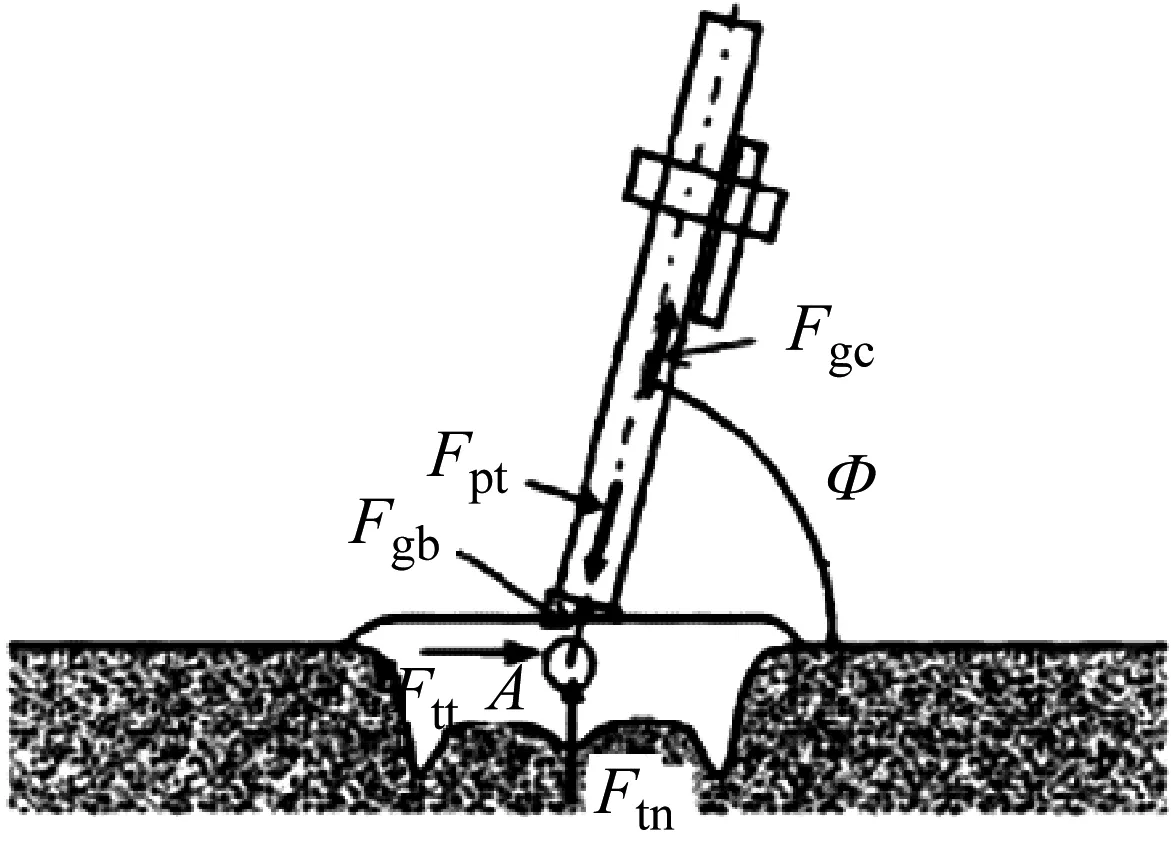
图1 座钣受力示意图
图1中:Fpt是炮膛合力;Ftn是土壤抗力的法向分力;Ftt是土壤抗力的切向分力;Fgc是除座钣以外的后坐部分的惯性力;Fgb是座钣惯性力;φ是高低角。假设后坐质心在身管轴线上,忽略惯性力作用,座钣的后坐力
F=Fpt+Fgc
(1)
式中,炮膛合力可分解为垂直于座钣平面的力和平行于座钣平面的力,得:
FptN=Fptsinφ
FptT=Fptcosφ
(2)
以往经验表明,座钣最大受力位置应出现在身管轴线方向的区域,应力较大的区域集中在座钣主钣和锥形盆连接的环形区域、驻臼周围区域、底部立筋与驻臼连接的部分及以上区域相接触的土壤中。
因此与座钣接触的土体中,取一个以该点为中心的微小的平行六面体,其六个面的外法线方向分别与三个坐标轴的正、负方向重合,各边长分别为x、y、z。假定应力在各面上均匀分布,各面上的应力矢量用作用在各面中心点的一个应力矢量来表示,每个面上的应力可分解为一个正应力和两个剪应力分量,如图2所示。

图2 土体中一点应力状态
该点的应力状态可以用六个剪应力分量和三个正应力分量组成应力张量来表示
(3)
式中:σ为应力张量;x、y、z分别为沿x、y、z坐标轴方向的三个正应力分量;其余量为剪应力分量,其脚标的第一个字母标明其所在面的外法线方向,第二个字母标明应力分量的指向。由于剪应力的互等性,应力张量为对称张量。相对应的,土体中一点的应变状态可以用九个应变分量来表示
(4)
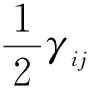
根据弹塑性理论的基本理论,土壤在屈服之前只产生弹性应变。本文假设与座钣接触土的力学性能在各个方向上是相同的,即将其视为各向同性材料。因此,其弹性力学的应力应变关系服从广义胡克定律,为:

(5)
式中:E为弹性模量;v为泊松比。
当土壤中一点的应力状态满足屈服准则就进入了塑性阶段,屈服准则规定了土壤开始出现塑性变形的应力条件,结合加卸载准则可以判定土的变形是弹性变形还是塑性变形。在迫击炮座钣的计算中,一般使用的屈服准则是D-P准则,因此需要对D-P准则中存在的不足进行修正。
1.2 迫击炮座钣建模
梯形棱锥座钣的主钣、锥形盆、立筋、包筋等部分组成了一个封闭结构,座钣外表面网格部分如图3所示,全座钣采用TC4钛合金,根据几何模型结构特征,各部件筋钣厚度如表1所示。座钣总结构质量为75.72 kg。座钣有限元模型的单元总数为23 650,节点总数为22 367。
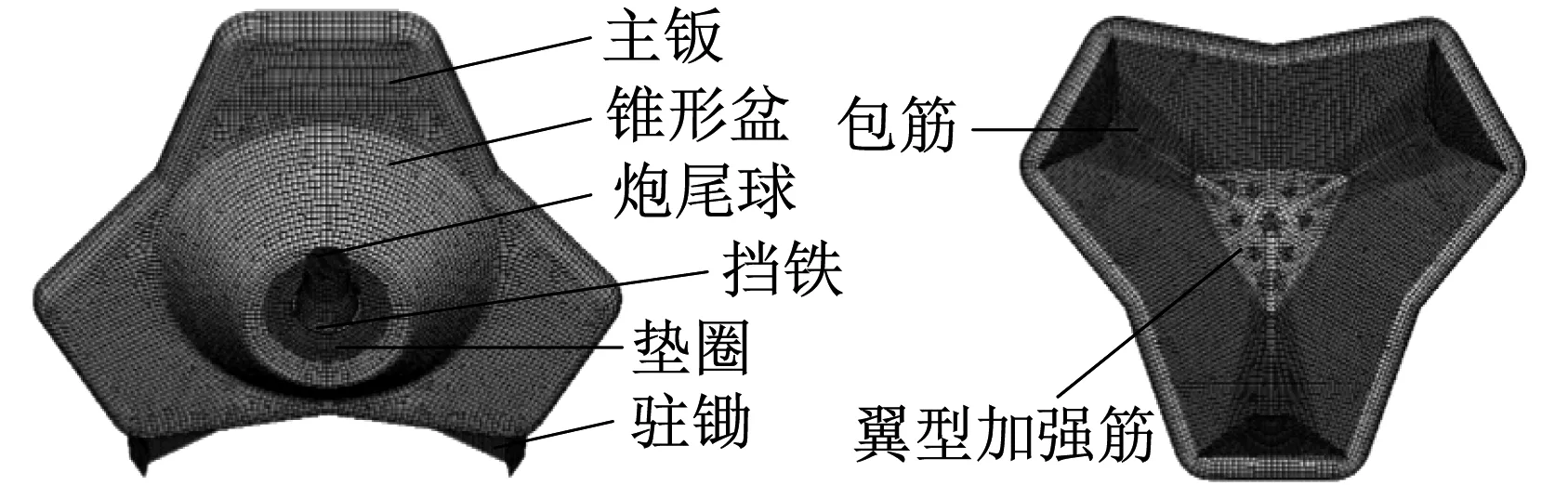
图3 座钣外部结构网格

表1 部件筋钣厚度
为准确计算试验所选取的工况下土壤的应力及变形,建立相应的有限元计算模型,如图4所示,除座钣外共14 627个单元,3 110个节点。

图4 座钣-土壤耦合有限元模型
2 D-P准则及其修正
2.1 D-P准则及其修正
M-C准则在三维空间的屈服面是不规则的六角形截面的角锥体表面,引入应力洛德角参数,M-C屈服准则[15]可以表达为
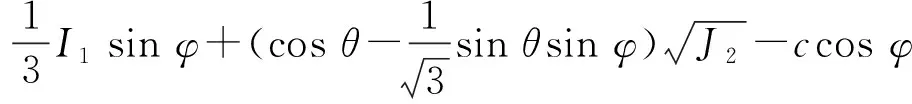
(6)
式中:I1为应力张量的第一不变量;J2为应力偏量的第二不变量;θ为洛德角,与应力状态有关,取值范围为[-π/6,π/6]。
D-P准则[16]是在Mise强度准则的基础上,考虑平均应力P或I1,具体表达式为
(7)
式中,α和k为材料参数
(8)
(9)
式中:c为土壤的黏聚强度;φ土的内摩擦角。M-C、D-P屈服面形状如图5所示。
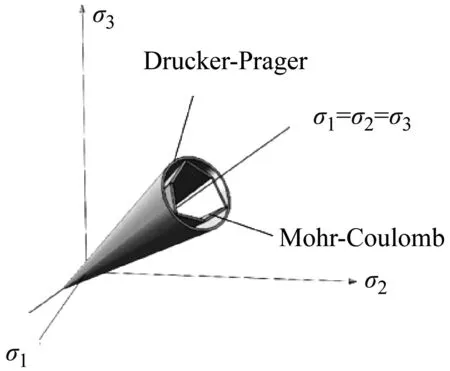
图5 M-C、D-P准则屈服面形状
对于此类问题,李平恩等提出的D-P-Y准则,分别用双曲旋转面和球形屈服面俩代替D-P准则在拉剪区的圆锥面,两种形式虽然处处光滑,但都在拉剪区改变了D-P准则的形式,缩小了传统的D-P准则的弹性区,所以有必要在这两种研究的基础上作出修改,保证D-P准则在拉剪区的形式,使其满足应力角效应,符合土壤的材料基本性质。有:
(10)
式中,g(θ)为角隅函数,也称为形状函数,它表示π平面上屈服曲线随洛德角θ变化的规律,表示破坏条件的形状。该函数的选择一般是根据试验结果来确定,同时必须满足以下3个条件才能保证π平面上屈服曲线外凸且光滑
(11)
引入适合该准则的角隅函数
(12)
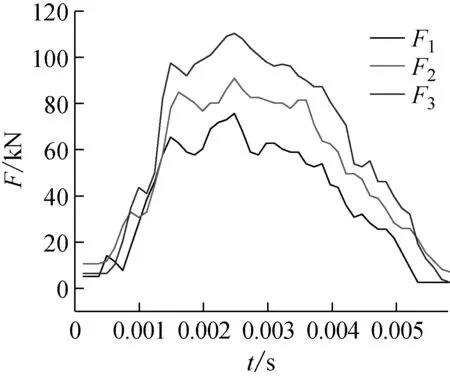
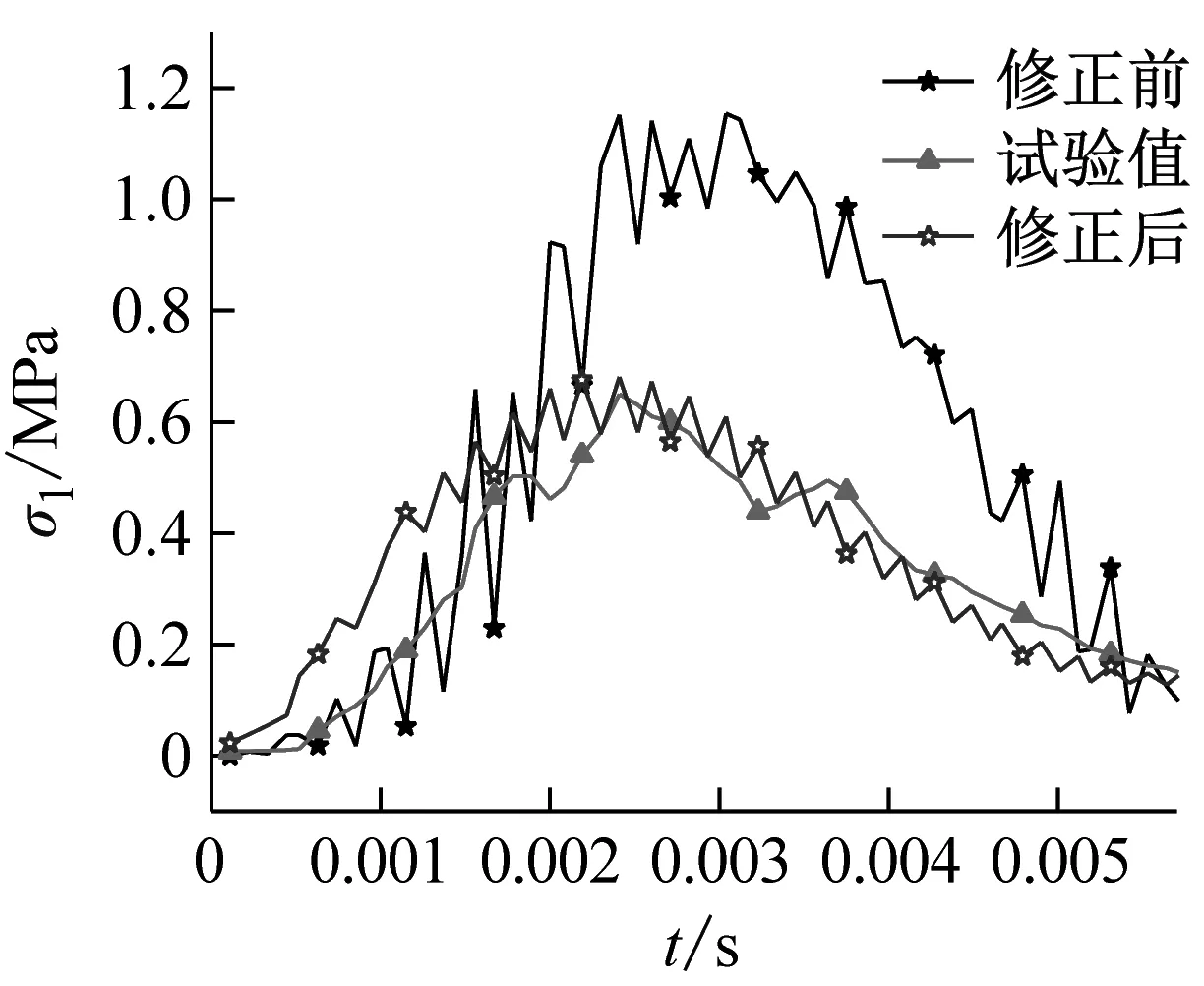
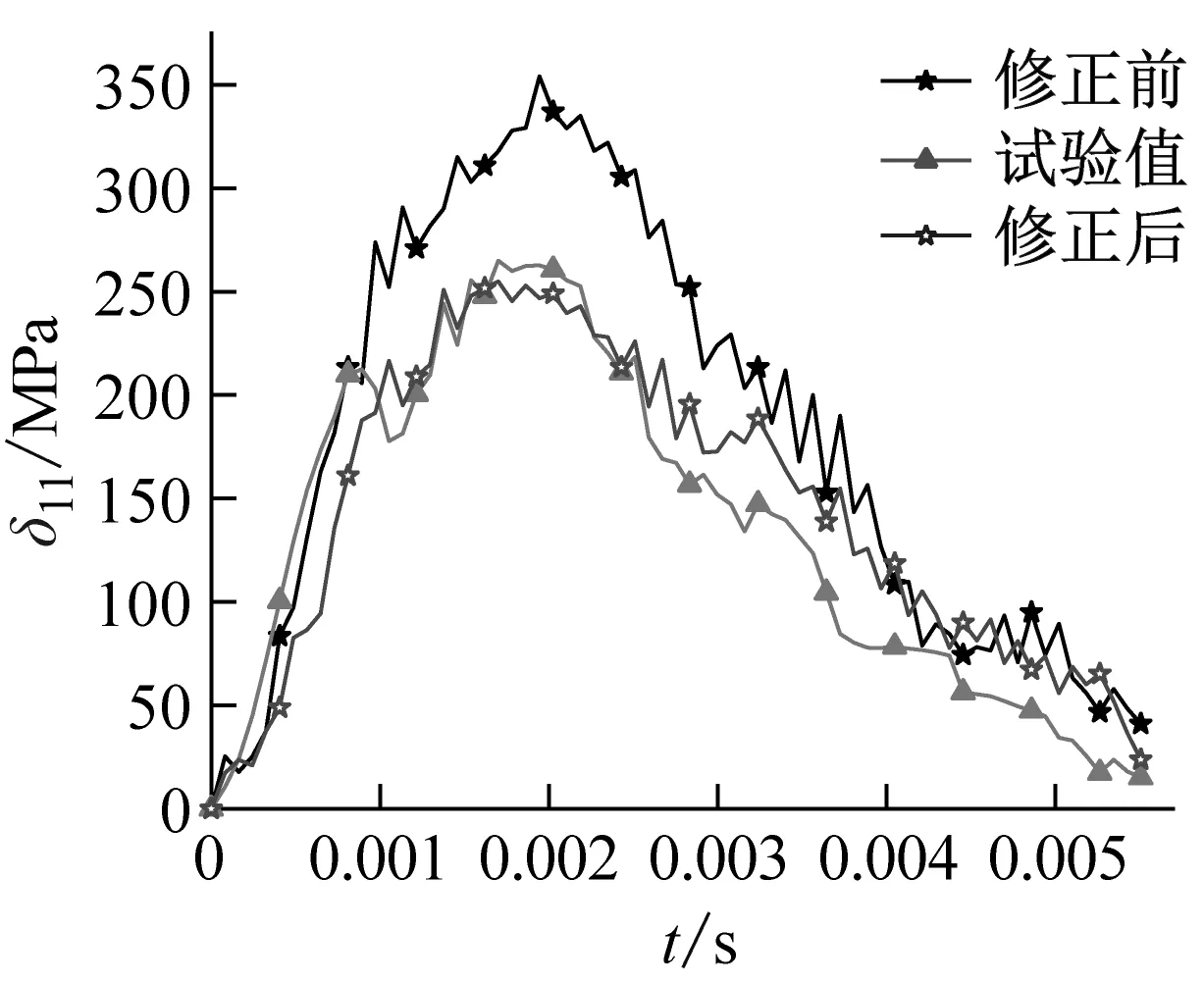
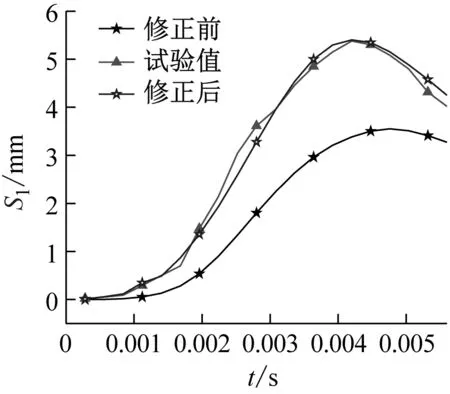
式中,0.7 (13) 该式可保证屈服准则式中经过单轴抗压强度点。由此,修正的D-P准则在子午面上如图6所示。 图6 修正的D-P准则 修正D-P准则的数值实现是在ABAQUS中提供的用户子程序中进行二次开发[17],运用弹性预测-塑性修正的思想,其计算流程如图7所示。 图7 数值实现过程流程图 步骤1给定初始条件,施加载荷,定义边界条件。迫击炮座钣的将载荷曲线施加在炮弹弹尾和尾翼中心截面,即炮尾球的上端面。炮尾球球面与驻臼球面之间、座钣与土壤之间均采用面面接触,土壤所在箱体采用全约束进行模拟。迫击炮一般采用45°~85°高低角射击,弹道十分弯曲。通过改变炮尾球与驻臼之间的接触角度来改变工况。由于座钣结构具有三角对称特性,考虑到迫击炮的圆周射击,在方向角上选择60°作为研究工况。 步骤2输入应力、应变增量Δδ、Δε; 步骤3计算分析步开始,增量步计算开始,进行弹性预测。在时间步长为n+1、迭代步为k+1时,应力为 (14) (15) 若此式成立,应力不需要进行塑性修正(塑性修正的目的是求解正确的应力,从而使屈服函数能在屈服面上),直接转入第七步。反之,需要进行塑性修正。 步骤5塑性修正。首先,求解塑性因子: (16) (17) 接着,更新内部变量 (18) (19) 步骤6内外力平衡判断,求解系统平衡方程。 (20) (21) (22) 式中:ToL是允许范围内的极小值;V是单元的体积。 为获得迫击炮发射时,座钣受冲击载荷作用下,土壤的应力与应变之间的关系,进行了座钣冲击试验,设计的试验总体方案如图8所示。 1-行架; 2-吊机; 3-电磁铁; 4-落锤; 5-冲击平台; 6-防护架; 7-土; 8-座钣; 9-炮尾球支柱; 10-土箱; 11-支架; 12-座钣; 13-位移传感器 试验装置主要由冲击装置、辅助装置、座钣、测试系统、中硬土和土箱等组成。用于模拟迫击炮发射时座钣所受强冲击载荷。辅助装置由冲击平台、防护架组成,用以保证载荷准确作用于座钣中心。测试系统由应变式力传感器、激光位移传感器、压电式土压力传感器、电阻式应变片、电荷放大器及数据采集仪等组成。力传感器安装在与驻臼接触的炮尾球支柱上平面;激光位移传感器固定在土箱箱体外的支架上,竖直方向投影在座钣的主钣上;压电式土压力传感器布置在座钣中心正下方约20 cm处,用以测量座钣受不同载荷作用时土壤的应力;电阻式应变片安装在座钣上驻臼与锥形盆的过渡区。试验过程如图9所示,包括试验现场(a)和数据采集(b),测得的载荷如图10所示,三次冲击作用下载荷的最大值分别为75.7 kN、90.8 kN、110.4 kN。 (a) 试验现场 图10 测得的载荷曲线 为较为准确地验证模型结果,将试验测得的载荷分别垂直施加在与座钣驻臼中心位置接触的炮尾球上端面上,但以目前的试验条件,需要设定90°高低角的计算工况,用来与试验工况进行对比。在ABAQUS有限元分析中,土壤的参数设定与试验相同,如表2所示。 表2 土壤主要参数 仿真计算得到不同载荷下土壤中测点所受应力、座钣上测点所受应力及位移量的修正前后的计算值与试验值对比如图11~13所示。应力最大值和位移最终值对比如表3所示。 (a) F1载荷下的应力对比 (a) F1载荷下的应力对比 (a) F1载荷下的应力对比 表3 试验值和计算值的对比 三种冲击载荷下,对应的应力和位移的变化规律相似。在0~0.002 5 s之间,应力计算值振荡上升,达到最大值;试验值逐渐上升至最大值,上升途中均出现一次小的波峰,但不超过最大值。0.002 5 s之后,计算值振荡下降并趋于稳定,该值均在0.15~0.2 MPa之间;试验值逐渐下降并趋于稳定,最终得到的值与计算值基本一致,下降途中均出现一次小的波谷,但均大于最终值。关于位移,试验值在0.004 s前不断上升,位移量达到最大,之后逐渐下降,座钣对应实现复进运动,得到最后的复进位移,计算值与试验值的位移规律基本一致。修正前,三种载荷下土壤中测点的应力最大值较试验值的误差分别为76.9%、109.7%、114.3%;座钣上测点的应力最大值较试验值的误差分别为35.1%、14.4%、24.1%;土壤中测点的位移最终值较试验值的误差分别为-18.7%、-20.6%、-30.1%。可以发现,修正前座钣下土壤中测点处的应力最大值和位移最终值的计算与试验值误差较大,且随着载荷值逐渐增大,两者的误差也逐渐增大。座钣上测点处的应力最大值与试验值也存在较大差距。而修正后,三种载荷下的土壤中测点的应力最大值较试验值的误差分别为4.6%、6.9%、6.5%;座钣上测点的应力最大值较试验值的误差分别为2.7%、4.2%、1.2%;土壤中测点的位移最终值较试验值的误差分别为5.7%、0.7%、4.0%。可以发现,三者之间误差都不超过7%,且没有随着载荷的增大而增大。修正后的计算值与试验值具有较好的一致性,提高了模型计算精度,因此,可基于该修正模型进行迫击炮座钣的设计研究。 本文为了提高某迫击炮座钣-土壤耦合模型计算的准确度,在修正D-P准则研究的基础上,使其符合土壤材料的基本性质,该准则的修正能够保证在拉剪区的形式,并满足压力角效应,本文将其首次应用到迫击炮座钣-土壤模型计算中。对座钣-土壤进行了受力分析,建立迫击炮座钣-土壤计算模型,利用材料本构接口,将修正的D-P准则嵌入其中,实现有限元数值模拟。进行了强冲击载荷下迫击炮座钣-土壤的动态响应试验,对比了不同冲击载荷下修正前后仿真与试验所得土壤中测点的应力和位移、座钣上测点的应力的数值。结果表明,将修正后的D-P准则应用在迫击炮座钣-土壤模型计算中可以较好地描述试验现象,提高迫击炮座钣-土壤耦合模型的计算精度,为座钣设计研究提供参考。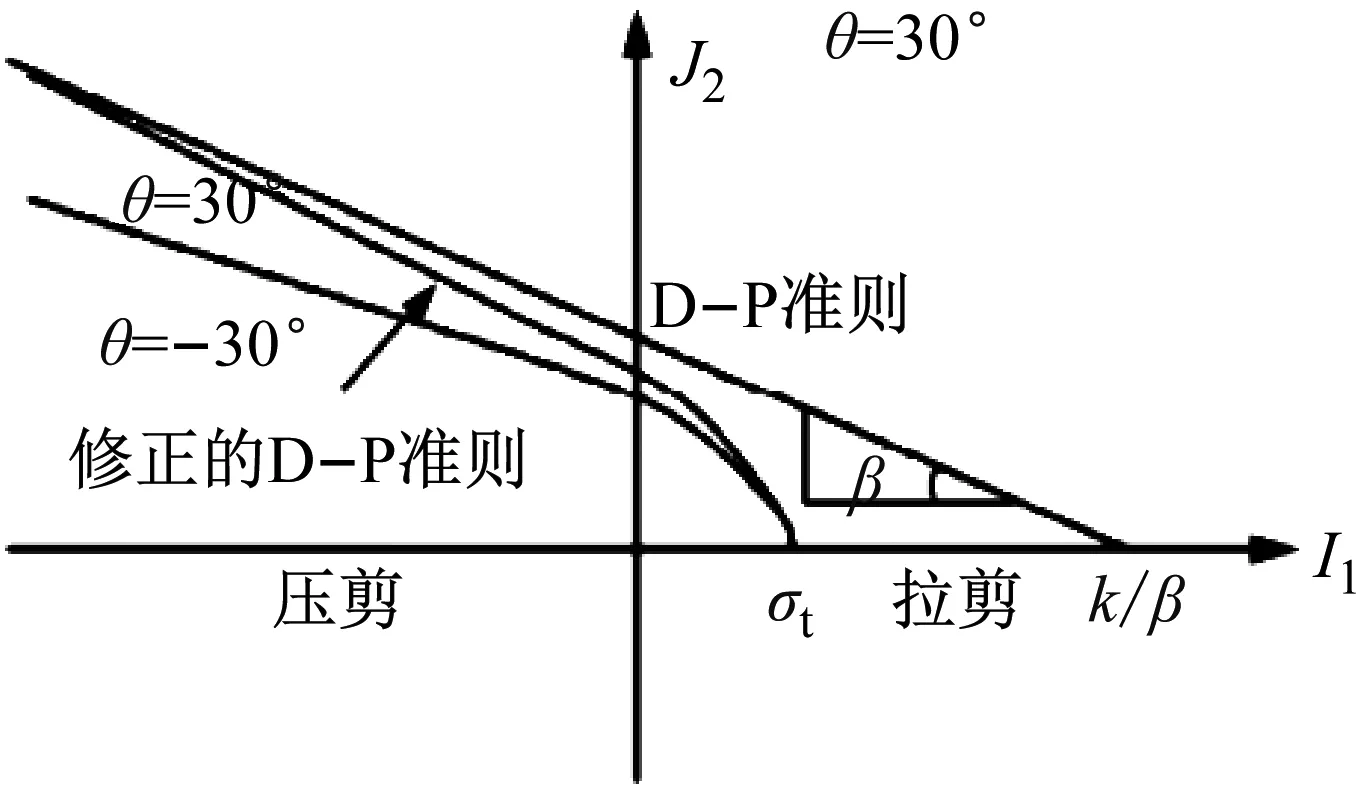
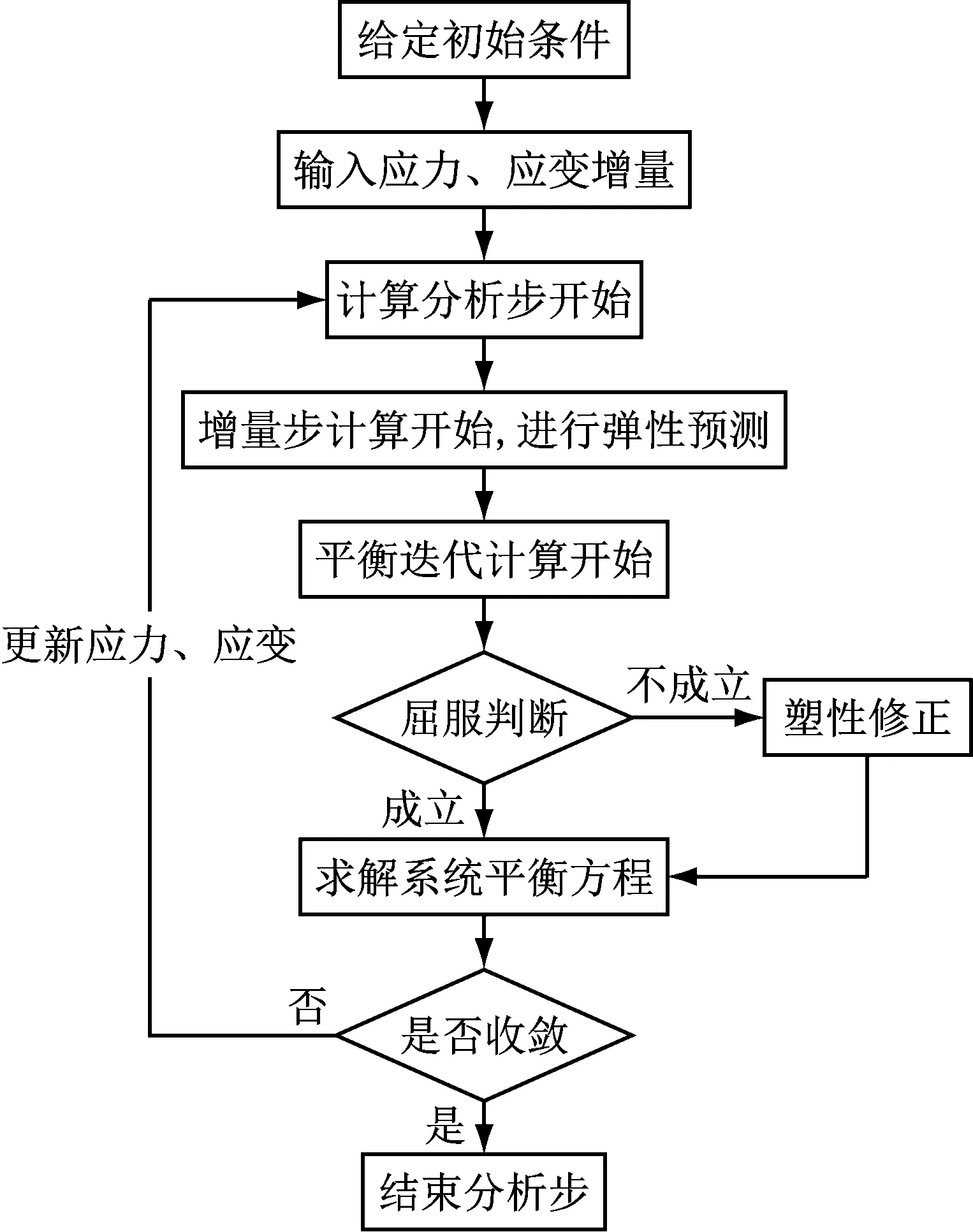
2.2 修正D-P准则的数值实现过程
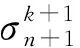
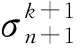
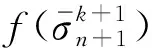
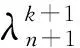
3 试验与结果分析
3.1 试验方案及实施


3.2 结果对比分析


4 结 论
