基于图像动态识别技术的地震动参数快速判别方法

刘济舟， 孟上九,,3， 袁晓铭， 王 淼， 孙义强

(1.中国地震局工程力学研究所 中国地震局地震工程与工程振动重点实验室，哈尔滨 150080；2.哈尔滨理工大学 建筑工程学院，哈尔滨 150080； 3.黑龙江科技大学，哈尔滨 150022)

地震是一种自然现象，强烈的地震会对城市系统造成巨大影响。地震动参数的快速判别，对地震灾害的评估，对地震科学考察的进行都有很大帮助。现在地震动参数信息的来源，主要是依靠各地区布设的地震台网及台阵。

已有学者研究指出，在目前的状况下, 实现地震预警的合理台间距为10～20 km。即使目前运行的测震台站和强震动台站都能参与地震预警, 但也只有北京、天津和上海地区和河北、云南、四川等地的部分台站密集地区, 能够满足地震预警的基本条件，地震台网的现状密度并不能满足地震预警的基本要求[1-2]。

随着天网监控系统的不断完善，各个中小城市的道路、建筑物侧边都有密集分布的摄像头，在地震灾害发生的时间点，除了台网和台阵的记录，这些摄像头也能实时记录地震灾害的全过程，里面的视频资料包含着大量地震的相关信息，这些信息要比从台网得到的资料要丰富得多。

同时随着5G时代的到来，传输数据速率快、网络延迟低、传输稳定性高的5G网络[3]，正好满足了视频资料的时效性要求，只要能掌握一定的分析处理方法，提取出视频中的地震相关资料，就能从另一个维度对地震动进行分析。与地震台网在震后给出的抽象的震级数据不同，公众对地震的了解，更多的是通过各地摄像头录制下的视频资料对地震产生的直观印象。因此，对录制视频进行地震资料的提取，也是符合大众群体要求的工作。

近年来，图像识别技术逐渐应用在地震工程领域。Ham等[4]提出,可以通过搭载高分辨率相机的无人机更新震后实时道路信息，为采取紧急救援提供准确、快速的实时信息；Naser[5]还提出了一种通过摄像机拍摄的室内画面，利用机器学习方法，对震后的房屋结构进行损伤评估的方法。此外，图像识别技术还被应用于震后基础设施健康监测与混凝土结构损伤判定[6-9]等工作之中。

以往研究主要通过震后的图像资料为救援或灾害识别提供参考，而没有对震中的图像资料进行采集与处理，因此无法提取到震中的地震相关信息。本文拟通过振动台的地震模拟试验和图像识别技术的相关原理，利用处于模拟地震震中的摄像头录制下的图像资料，提取地震动的相关信息，并提出一种基于图像动态识别的地震动参数快速判别方法，为灾害评价、地震动信息获取和建筑物地震安全监测提供技术支持。

1 原理介绍

本试验主要目的是利用图像识别技术得到准确的振动台加速度。图像识别技术在振动台试验中的应用，主要用于监测结构在振动台模拟地震下的变形和位移[10-12]。本文为了模拟真实地震下的摄像头情况，需要将摄像头置于振动台之上。随着振动台的运动，摄像头也在不断振动，这就要求我们对摄像头进行运动补偿，即通过对摄像头进行结构动力学分析的方式，确定其运动轨迹，从而对图像做出对应修正，达到分析振动台真实位移时程的目的，提出一种基于地震中的动态视频资料识别地震动参数的方法，这也是本文的创新点和立足点。

1.1 单自由度体系振动计算方法

振动台带动摄像头运动的过程中，涉及到结构受迫振动的计算问题。单自由度体系振动是结构动力学的基本问题，在特定的坐标系下，单自由度系统也能表现出与多自由度系统和无限自由度系统的相似性态[13]。因此，本试验按照单自由度体系计算结构在振动台输入波下的受迫振动。

受迫振动指系统在持续的外界控制的激励作用下所发生的振动。本试验中，由振动台提供与振动系统本身无关的外界激励。受迫振动方程

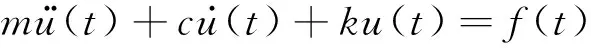
(1)

由受迫振动方程，在忽略阻尼的情况下，我们只要知道了结构的质量、刚度参数和输入的外界激励，就能得知物体的运动状况。

1.2 动态图像识别原理

1.2.1 动态图像预处理

通过摄像头录制下来的视频，需要进行一定预处理工作，才能对其进行图像识别。工作主要包括：

动态视频分帧提取。帧是动态视频中最小单位的单幅影像画面。视频由若干个单帧图片组成，按照摄像机的帧率，将每一帧的图像提取出来，再对其进行图像处理工作。

图像灰度化处理。分帧得到的视频图片都是采用RGB颜色模式，如果直接处理彩色图像，要分别对RGB三种分量进行处理。灰度值指黑白图像中点的颜色深度，范围一般从0～255。将图像做灰度化处理，就只需处理以灰度值作为参数的图片，可以大幅提高图像识别的运算速度。

图像裁剪。摄像机的分辨率较高的情况下，图片中包含的信息很多，采用全图进行分析的话，会拖慢图像识别的运算速度。在进行图像处理之前，选择感兴趣的部分对图像进行裁剪，也可以提高图像识别的运算速度。

1.2.2 模板匹配

图像识别要解决的问题，就是用机器代替人去认识图像和找出一幅图像中人们感兴趣的目标物。利用图片中的模板子图像，通过计算模板子图像的灰度值矩阵在图片整体灰度矩阵的相关度，在图片中寻找模板子图像的中心位置[14]。图1即为本试验的模板子图像选取。

图1 模板子图像选取

确定视频每一帧处模板子图像(本试验选取台面标记点图像作为模板子图像)的位置，便可以得到以像素点为单位的摄像头位移时程。

1.2.3 坐标系转换

摄像头以像素点为单位的位移时程，所在的坐标系是像素坐标系[15]。通过量取摄像头摆放的相关参数，结合相机的性能参数，将以图片左上角为坐标原点的像素坐标系转化成以相机所在空间位置为坐标原点的相机坐标系。

像素坐标系和相机坐标系的转换关系为

(2)

式中：s为单个像素点的宽度(高度)；u，v为计算点在图片中的像素点位置；f为焦距；Ox,Oy为图像中心点的像素点位置；Xc,Yc,Zc为计算点在相机坐标系中的坐标值；Mint为摄像头的内部参数矩阵。

在本试验中得到模板图像在相机坐标系中的位置后，利用几何学知识，计算出以摆动角度为单位的摄像头运动时程，如图2所示。

图2 根据相机坐标系计算摄像头摆动角度

1.3 结构运动模型

本试验采用的是如图3所示的单自由度结构模型，能得到振动台运动和摄像头运动的转换关系

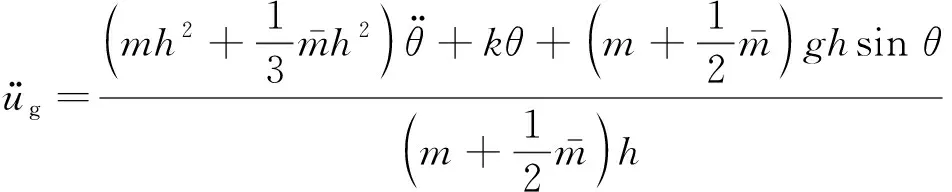
(3)

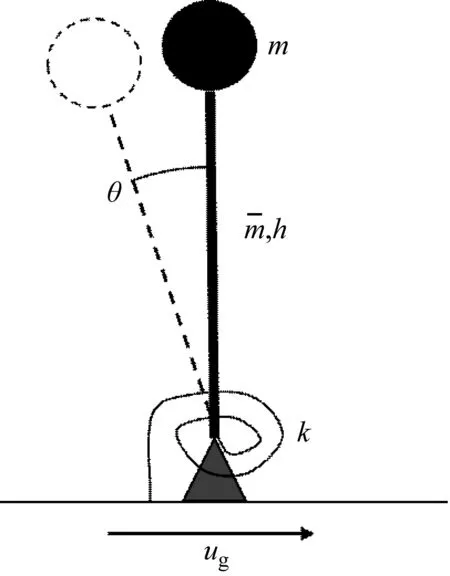
图3 摄像头-振动台结构的运动模型

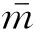
通过摄像头-振动台运动模型的建立，结合以摆动角度为单位的摄像头运动时程，就能得到摄像头在世界坐标系中的运动轨迹，从而实现摄像头的运动补偿，并对模板图像所在的灰度矩阵做出对应修正。

1.4 滤波

滤波是将信号中特定波段频率滤除的操作，是抑制和防止干扰的一项重要措施，在信号处理和图像识别的领域，都有着广泛的应用。

一般来说，摄像机的帧速率比输入地震动频率要高得多，会产生大量高频段噪声，在利用位移时程计算加速度时程时，会产生很大误差，因此，要对处理出图片素材进行滤波操作。

本试验采用的滤波方法是低通滤波，用于去除图像中的高频成分。其具体操作是，对图像进行傅里叶变换(FFT)，得到频谱，再用理想低通滤波器对频谱滤波，之后对滤波后的频谱进行反傅里叶变换(IFFT)，得到滤波后图像，滤波前后的结果对比如图4所示。

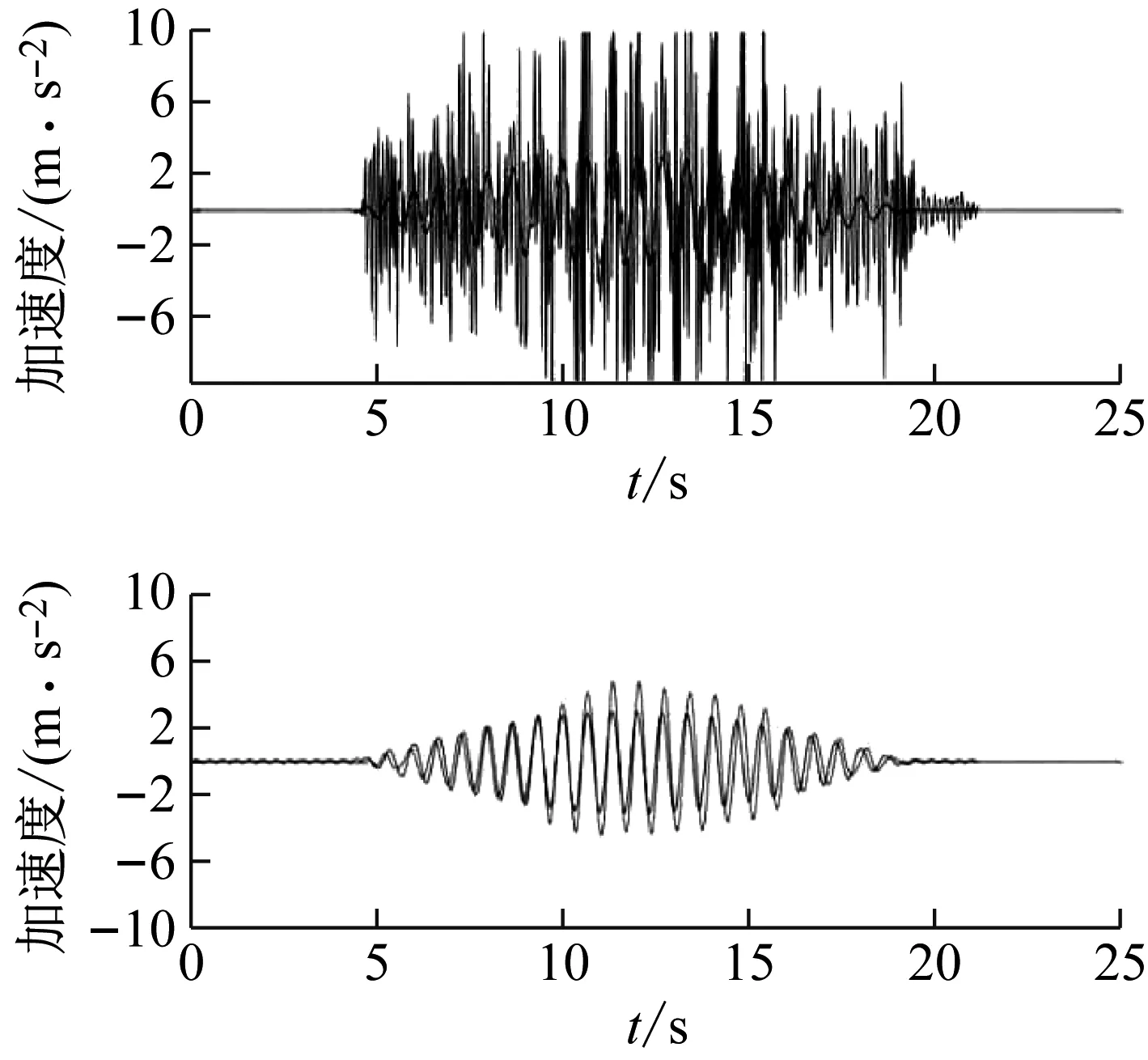
图4 滤波前后的加速度时程对比

2 模拟试验

2.1 试验设备参数

试验使用摄像机采用的是Logitech c930e高清摄像头，具体参数如表1所示。

试验使用的是伺服电机驱动振动台[16]，其主要性能参数如表2所示。

表2 伺服电机驱动振动台性能参数

试验使用数据采集器使用日本TML公司的便携多功能TMR200采集仪，其采样频率为1 Hz～1 kHz，在本试验中，采样频率为1 kHz。

2.2 试验设备布置

摄像头通过可伸缩的支架固定在振动台上，并与放置在振动台外的电脑进行连接，存储录制下的视频；振动台上粘贴一标记点，作为图像识别的模板图像；在与振动台相同高度的振动台外固定一位移传感器，并与数据采集器连接，用于测量振动台的位移时程。

具体的试验设备布置如图5所示。

图5 试验设备布置

2.3 试验方案

在实际的地震过程中，拍摄点位置以及地震波的各种参数都存在一定差异，为论证图像识别方法的可靠性，本试验在不同高度的摄像头，不同输入波形的振动台的条件下，对采集到的视频资料进行收集、整理、分析。

本试验的振动台波形，分别选择了频率为1.5 Hz、2.0 Hz、3.0 Hz的正弦波和正弦拍波，共计6种波形；摄像头高度选择了80 cm、100 cm、120 cm、140 cm四种高度，试验组数共24组。

2.4 试验步骤

(1) 将摄像头旋转到台面标志点的方向，尽量使参照物影像落在图像中心位置，之后准备开始录像；

(2) 先启动摄像头连接电脑中的视频录制软件，然后开启振动台并启动数据采集器，记录振动台的位移时程；

(3) 振动台震动结束后，结束视频录制软件和振动台数据采集仪的记录，作为一组试验；

(4) 改变摄像头的高度和振动台输入波形，重复上述步骤，进行多组试验。

3 试验结果及分析

通过模拟试验，得到了振动台加载不同频率，不同波形下，位于不同高度摄像头的录制视频，通过图像识别、结构动力学相关原理，得到振动台计算加速度时程，与通过数据采集器得到的振动台实测加速度时程进行对比，绘出加速度时程对比曲线并对峰值加速度进行对比。

3.1 实测加速度时程与计算加速度时程对比曲线

3.1.1 振动台输入正弦波下的加速度时程分析对比

振动台输入波形选择频率分别为1.5 Hz、2.0 Hz、3.0 Hz的正弦波时，在不同摄像头高度下的加速度时程分析对比结果如图6～图8所示。

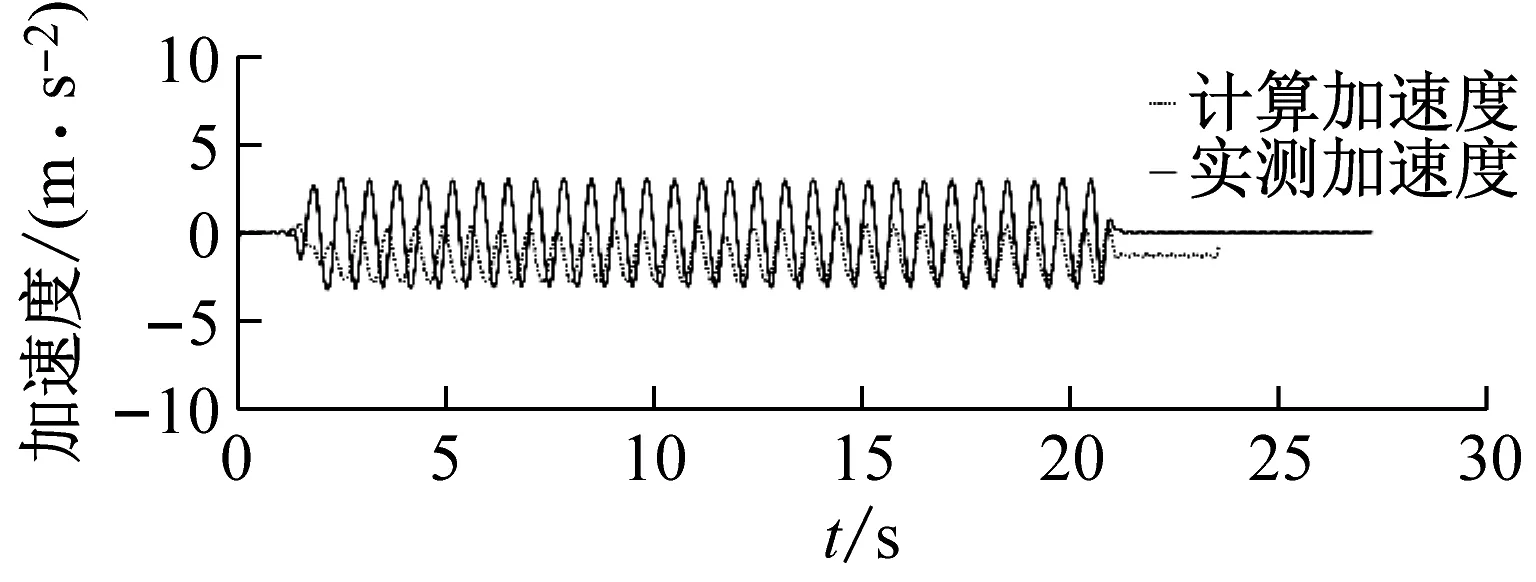
(a) 摄像头高度80 cm

(b) 摄像头高度100 cm

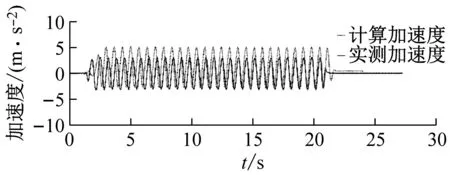
(c) 摄像头高度120 cm

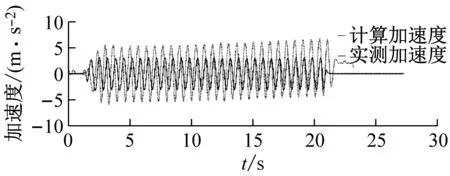
(d) 摄像头高度140 cm

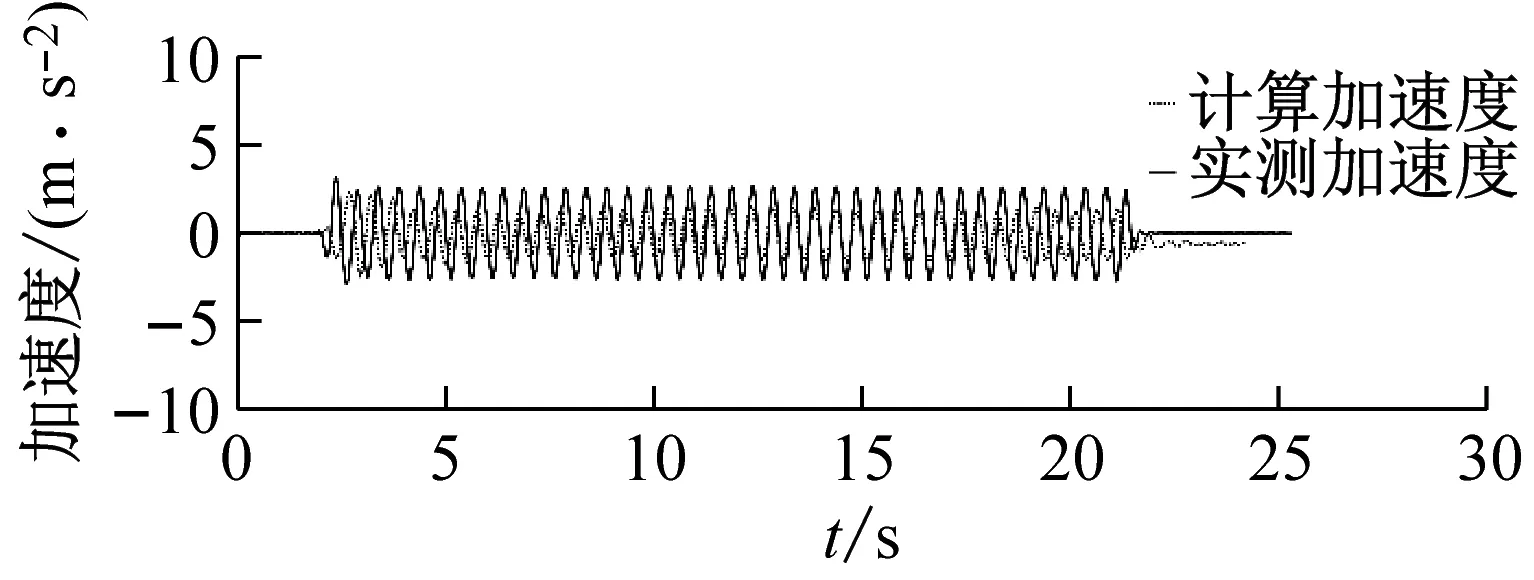
(a) 摄像头高度80 cm

(a) 摄像头高度80 cm

从图6～8中可以计算得到，振动台输入正弦波为1.5 Hz时，实测峰值加速度为3.213 3 m/s2，当摄像头高度分别为80 cm、100 cm、120 cm、140 cm时，其计算峰值加速度分别为3.745 7 m/s2、3.620 6 m/s2、5.167 1 m/s2、6.593 1 m/s2，对应的误差分别为16.57%、12.12%、60.80%、105.18%；

振动台输入正弦波为2.0 Hz时，实测峰值加速度为3.156 6 m/s2，当摄像头高度分别为80 cm、100 cm、120 cm、140 cm时，其计算峰值加速度分别为2.457 0 m/s2、4.591 2 m/s2、3.256 4 m/s2、3.601 1 m/s2，对应的误差分别为22.16%、45.45%、3.16%、14.08%；

振动台输入正弦波为3.0 Hz时，实测峰值加速度为2.079 5 m/s2，当摄像头高度分别为80 cm、100 cm、120 cm、140 cm时，其计算峰值加速度分别为1.677 0 m/s2、1.930 9 m/s2、1.290 4 m/s2、2.001 3 m/s2，对应的误差分别为19.36%、7.15%、37.95%、3.76%；

可以看出，在振动台输入正弦波的12组数据中，计算加速度峰值有9组误差在40%以内，有2组在40%～80%，只有1组数据在80%以上，图像识别技术的识别效果和稳定性都较好。

3.1.2 振动台输入正弦拍波下的加速度时程分析对比

振动台输入波形选择频率为分别为1.5 Hz、2.0 Hz、3.0 Hz的正弦拍波时，在不同摄像头高度下的加速度时程分析对比结果如图9～图11所示。

(a) 摄像头高度80 cm

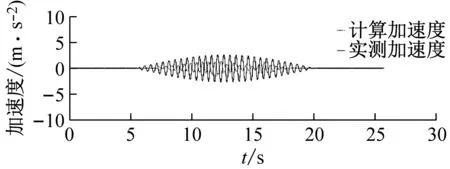
(a) 摄像头高度80 cm

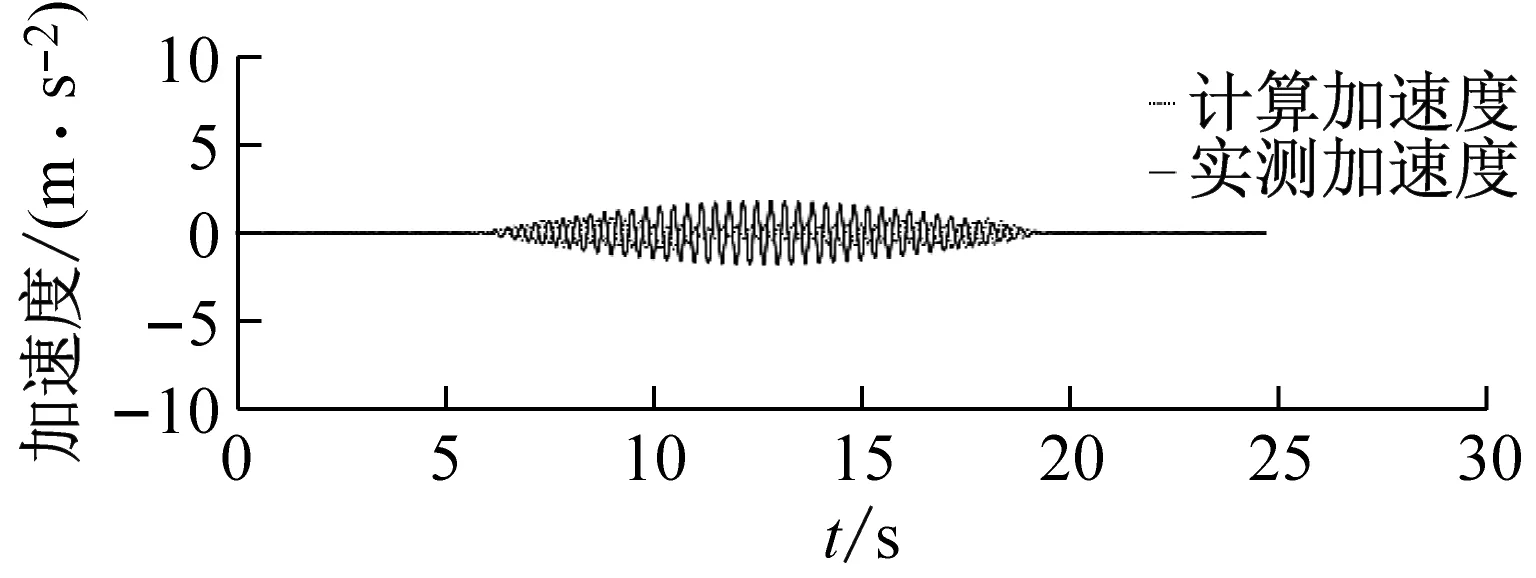
(a) 摄像头高度80 cm

从图9～11中可以计算得到，振动台输入正弦拍波为1.5 Hz时，实测峰值加速度为3.083 7 m/s2，当摄像头高度分别为80 cm、100 cm、120 cm、140 cm时，其计算峰值加速度分别为2.704 0 m/s2、3.246 2 m/s2、4.586 7 m/s2、5.458 8 m/s2，对应的误差分别为12.31%、5.27%、48.74%、77.02%；

振动台输入正弦拍波为2.0 Hz时，实测峰值加速度为2.662 9 m/s2，当摄像头高度分别为80 cm、100 cm、120 cm、140 cm时，其计算峰值加速度分别为1.796 1 m/s2、4.235 0 m/s2、2.689 5 m/s2、1.853 3 m/s2，对应的误差分别为32.55%、59.04%、1.00%、30.40%；

振动台输入正弦拍波为3.0 Hz时，实测峰值加速度为1.830 6 m/s2，当摄像头高度分别为80 cm、100 cm、120 cm、140 cm时，其计算峰值加速度分别为1.583 1 m/s2、1.434 8 m/s2、1.690 5 m/s2、1.431 5 m/s2，对应的误差分别为13.52%、21.62%、7.65%、21.80%；

可以看出，在振动台输入正弦拍波的12组数据中，计算加速度峰值有9组误差在40%以内，有3组在40%-80%之内，图像识别技术的识别效果和稳定性都较好。

3.2 计算加速度峰值与实测加速度峰值对比结果汇总

将得到的实测加速度峰值、计算加速度峰值以及误差数据按不同摄像头高度汇总成表，如表3所示。

表3 实测加速度峰值与计算加速度峰值对比结果汇总

3.3 摄像头高度和频率影响分析

本试验通过不同输入波形、不同输入波频率、不同摄像头高度的条件下，利用图像识别原理对摄像头所在振动台的振动参数进行分析计算，根据在不同工况下图像识别计算结果与实测结果的对比，绘制出相对误差值随摄像头高度分布和随振动台输入波频率、波形分布的散点图，如图12和图13所示；从图中得到以下结论：

图12 相对误差值随摄像头高度分布散点图

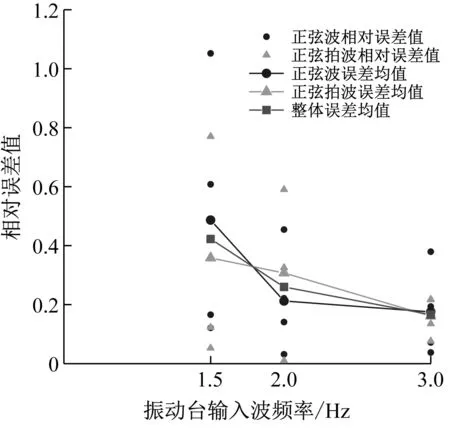
图13 相对误差值随振动台输入波频率、波形分布散点图

(1) 随着摄像头高度的增加，相对误差呈增大的趋势，原因是：随着高度的升高，相同大小的被拍摄物在图片中占据的像素点数量越少，从而对模板子图像中心所在的像素点坐标分析产生的误差增大，导致后续步骤误差增大；

(2) 随着摄像头的高度增加，误差值的波动幅度不断增大，原因是摄像头支架与振动台的接合处存在微小晃动，产生了随机误差，并且随着支架高度的升高，将整体的随机误差放大；

(3) 减少振动台的输入波频率，振动台的峰值加速度随之增加。相机的运动加速度越大，相同曝光时间内的图像复杂程度越高，导致图像模糊，降低了图像识别精度，从而产生误差。因此，随着振动台输入波频率增加，相对误差值呈减小的趋势；

(4) 在振动台输入波频率不变的情况下，相对误差值和振动台的输入波形并没有明显关系。

4 结 论

本文对置于振动台上的摄像头录制的动态视频进行分析，能在一定程度上反映真实地震时的摄像头录制情况，再通过本文中计算结果与实测结果的对比发现，利用图像识别技术这一分析方法，在对摄像头安装方式和安装位置了解较为清楚的情况下，可以在可接受的误差范围内对不同频率的地震动参数进行识别。如果能够根据摄像头的高度不同，设置相应的模型刚度修正系数，还可以进一步提高其精度。

现在我国摄像头的布置遍布大街小巷，而且安装方式都大致相同。地震发生时，摄像头录制的视频数据资料丰富，时效性强，覆盖面广，如果这一技术能得到应用与推广，几乎能够估算城市中在地震过程中所有位置、所有时间点的地震动参数，这对将来地震灾害的预防与评估、地震烈度区划的划分都有着重要意义。如果这一技术的精度能够进一步提高，就能作为台网、台站以外的补充手段对地震动参数进行分析，提供的有效数据量甚至能在台网、台站之上，有非常好的应用前景。

近年来，关于城市抗震韧性的研究发展迅速， 已经成为国内外地震工程研究领域的研究热点[17]，其中便涉及到抗震韧性城市设计地震动参数等问题，利用城市摄像头中提供的大量地震相关数据，可以避免计算复杂的场地效应、地震波传播介质等问题，直接通过曾经发生过的地震录像，计算城市中各点的地震动响应，也能为城市抗震韧性的研究提供一种新的思路。