半球谐振子固有刚性轴方位角测量方法与仿真研究

2022-03-18朱蓓蓓楚建宁王宜新汪学方许剑锋

振动与冲击 2022年5期

朱蓓蓓，楚建宁，秦琳，王宜新，陈肖，汪学方，许剑锋

(1.上海航天控制技术研究所,上海 201109；2.华中科技大学机械科学与工程学院,武汉 430074)

半球谐振陀螺是一种利用固体振动驻波的进动效应进行角速度测量的新型振动陀螺，它具有结构简单、可靠性好、抗冲击能力强、启动时间短、精度高、使用寿命长等众多优点，是目前高精度、小体积、长寿命陀螺的研究热点。其没有耗损部件、结构简单且具有较高的导航精度，决定了其在航空、航天、战略武器等领域具有独特优势，特别是在卫星、空间站、太空望远镜、月球探测等需要长时间稳定可靠运行的使用环境中，具有广阔的应用前景[1-5]。

半球谐振子是半球谐振陀螺的核心部件，在实际加工过程中产生的几何误差以及材料的各项异性，会导致半球谐振子在工作模态产生频率裂解[6]，将严重降低半球谐振陀螺性能指标，导致陀螺漂移，影响陀螺精度。频率裂解会使半球谐振子的二阶弯曲振型出现两个互相呈45°夹角的固有轴系，两固有轴系对应的二阶弯曲模态谐振频率分别达到极小值和极大值,其相对应的固有轴分别被称为低频轴(重轴)和高频轴(轻轴)[7-8]。研究表明若保证主驻波一直在谐振子的刚性轴位置，可有效降低频率裂解对谐振子振型的影响，能有效抑制谐振陀螺的漂移[9-10]，因此确定谐振子固有刚性轴方位对提高谐振陀螺制造精度具有重大意义。

目前有不少专家学者对谐振子频率裂解修调和固有刚性轴定位进行了理论分析，但对于谐振子固有刚性轴方位角的测量方法的研究较少。在林振等对质量不平衡对称壳体谐振子的频差消除研究[11]中采用压电片激励，使用一对相距180°的压电片以谐振频率激励，使用激光多普勒测振仪测量四个波腹位置的振幅，通过调整激励位置，使四个波腹位置的振幅值在同一水平，利用此方法确定四点调平法去除质量缺陷的位置(重轴对应位置)，但此方法需要在谐振子上粘贴压电片，会影响谐振子振型，降低固有轴定位精度；俄罗斯马特维耶夫提出了基于幅频特性和相频特性曲线的固有刚性轴和频率裂解的确定方法，采用激励电极和检测电极粘贴在谐振子上进行激励和检测振动信号，其装置成本高且算法复杂；李绍良等提出一种基于幅频响应特性的谐振陀螺频率裂解和固有刚度轴方位角测定方法，其采用压电激振台在谐振子频率附近进行扫频，利用多普勒激光测振仪绘制幅频响应曲线，最终利用拟合方程解算出固有刚性轴方位角；李巍等提出采用固定位置安装两组激励电极以及两组位移传感器对频率裂解以及固有刚性轴位置进行测定[12]，其提出的方案大大简化了利用静电激励的测试方案，但没有给出具体的测试过程和结果。以上测量方法大多采用压电与静电激励，操作复杂且成本相对较高，贴片压电激励方式还会对谐振子振动性能有一定的影响[13]。

本文根据俄罗斯马特维耶夫提出的半球谐振子位置激励模型，基于二自由度弹簧-质量系统振动模型，推导了谐振子唇缘位置的振动方程，通过有限元仿真模拟固有刚性轴测定过程，绘制具有质量缺陷的半球谐振子的幅频特性曲线；基于幅频响应特性设计了测量半球谐振子固有刚性轴的试验，采用非接触的声激励方式进行连续扫频激励，使用激光多普勒测振仪提取谐振子唇缘振动信号，结合幅频曲线特性和驻波波节点的振幅的变化规律，解算得出谐振子固有刚性轴方位角。本文采用的激励方法避免了与谐振子的直接接触，对数据的处理也相对简单，对已有测量方法的不足给予了很好的补充。

1 半球谐振子固有刚性轴测量理论分析

1.1 半球谐振子二阶模态数学模型

理想半球谐振子球壳上四波腹振动(二阶弯曲振动)模态应仅有一种频率，在球壳周向任意圆周角处激励谐振子都能得到稳定的二阶弯曲驻波振动。但在实际加工过程中，由于材料各向异性及加工几何误差导致谐振子圆周方向出现两个相互呈45°角的固有轴系，使得沿这两轴系的四波腹振动模态的振动具有不同的谐振频率。本文将半球谐振子二阶弯曲振动模型简化为二自由度弹簧质量系统，如图1所示，通过对该系统进行数学建模分析，为固有轴测量方法建立理论基础。在谐振子动力学方程中，沿两固有轴系方向的四波腹振动的方程是按圆周角和相位正交的，因此无角速度输入的半球谐振子激励模态与敏感模态的振动可等效为二自由度系统坐标轴处的受迫振动。

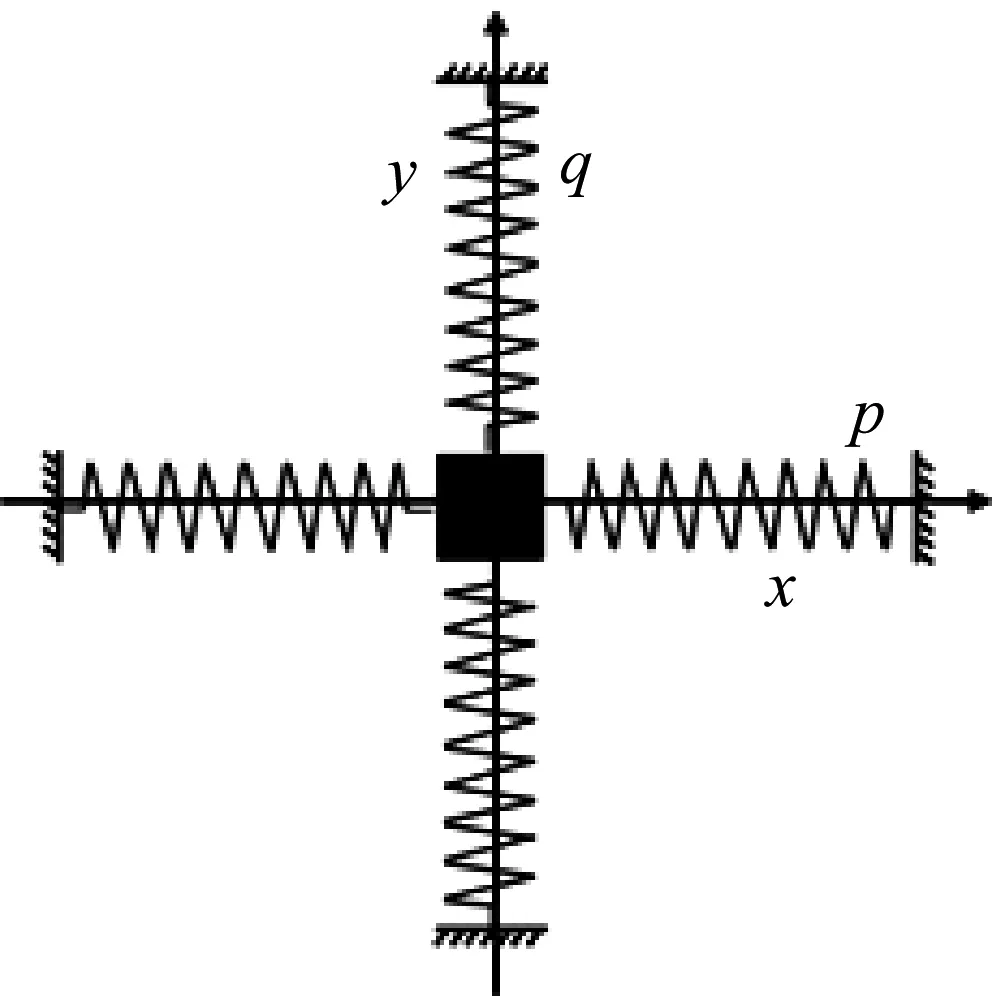
图1 二自由度弹簧-质量系统

假设此系统固有频率ω1≠ω2，激励位置与固有刚性轴之间的夹角为φ0，则此振动系统的受迫振动方程为

(1)

式中：λ为激励频率；p(t),q(t)分别为该系统沿坐标轴方向的振动方程，即等效的谐振子两固有刚性轴系对应二阶振型的振动方程，其谐振频率分别为ω1，ω2。

函数p(t)和q(t)的稳态解形式为

p(t)=|A|sin(λt-θ1)

q(t)=|B|sin(λt-θ2)

(2)

将式(2)代入式(1)可求出A，B，θ1和θ2在初始条件p(0)=0，q(0)=0情况下为

(3)

因此谐振子半球唇缘径向振动位移的表达式可以简化为下列公式

R(φ,t)=|A|sinλtcos 2φ+|B|sinλtsin 2φ

(4)

半球壳体谐振子，在四波腹振型(n=2)的振动中，φ为固有轴方位与激励位置之间的夹角，当激励固定于某一位置时(即φ=φ0)，采用扫频激励，此时唇缘的径向振动位移可简化表示为：

R(λ,t)=|A|sinλtcos 2φ0+|B|sinλtsin 2φ0

(5)

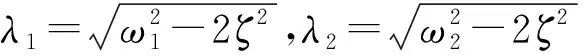
利用式(5)，通过数值仿真的方法绘制幅频响应曲线，通过设置频率范围为3 050～3 060 Hz，频率变化设置为时间的函数即λ=2π(kt+3 050)，令k=0.001(Hz/s)、F0=1、ω1=6 108π(rad/s)、ω2=6 112π(rad/s)，将损耗因子设置为定值ζ=0.1 ，可通过MATLAB数值仿真改变角φ0得到不同角度位置的振动信号仿真，图2所示为φ0=20°、45°时的振动信号仿真图，与上述推理结果吻合。

(a) φ0=20°

1.2 固有刚性轴测量方法分析

以上通过简化模型分析了谐振子沿两固有轴系的四波腹振动，如图3(a)所示为固有轴系与坐标轴重合的情况，p(t)、q(t)分别为两固有轴系处对应二阶模态的振动函数，两固有轴系四波腹振动的谐振频率分别达到极大与极小值，两谐振频率之差即为频率裂解。由以上理论模型可知，当激励位置与固有刚性轴不重合时，若采用扫频方式进行激励，则两固有刚性轴方向的振型将在对应频率下被不同程度激励起，如图3(b)所示。通过对唇缘沿圆周不同位置的径向振动信号进行分析，即可实现对谐振子固有刚性轴位置的测定。

(a) 刚性轴与坐标轴重合 (b) 刚性轴与激励位置不重合

当激励轴线很靠近某一固有刚性轴时，另一刚性轴处被激励起的振型越来越微弱，以至于不能从其幅频曲线中观察到两个峰值。因此，为了提高测量精度，可在使用扫频方法粗略确定固有刚性轴方位角的基础上，通过在固有轴位置附近使用该固有轴自然频率的正弦信号进行激励，检测与激励位置圆周相距45°位置波节点的振幅。由于激励位置不断逼近固有刚性轴方位时，其波节点的振幅将不断减小，因此可通过此方法进一步精确测定固有轴方位角。

1.3 固有刚性轴测量试验设计

本试验将采用扬声器在水平方向上对谐振子进行连续扫频激励，使用激光多普勒测振仪对谐振子半球壳唇缘的径向振动信号进行实时采集。按照图4所示的测量原理图，搭建半球谐振子固有刚性轴检测平台，检测平台及设备如图5所示。试验中通过信号发生器设置激励参数，通过功率放大器将信号发生器产生的正弦激励信号放大，使扬声器产生同频率的声波信号，激励金属谐振子振动，使用激光多普勒测振仪检测谐振子半球壳唇缘的径向振动。

(a) 波腹点测量

图5 测量平台及装置实物图

具体试验将按以下步骤进行：

步骤1通过仿真已经粗略确定了谐振子的工作频率，通过设置频带较宽的扫频信号，观察其幅频曲线，调节参数确定一个合适的频带和时间参数。

步骤2按图4(a)中装置位置示意图调整平台，转动转台选择一初始刻度对齐并记为初始0°，沿顺时针方向在0°～90°范围内每次转动转台5°进行一次测量。

步骤3通过步骤2的测量得到的幅频曲线特性确定两个固有刚性轴系所在角度范围，按图4(b)装置位置示意图调整测量平台，采用正弦信号在该角度范围内以恒定频率进行激励，每次转动转台1°进行测量。

2 试验结果与分析

2.1 固有轴测量的有限元仿真

根据测量试验的设计，利用有限元谐响应仿真模拟水平方向的扫频激励过程。通过添加集中质量构建质量分布不均缺陷，使有限元模型产生两个方位确定的固有刚性轴系，在固有刚性轴附近模拟水平方向的扫频激励过程，提取谐振子唇缘不同角度位置的幅频响应。使用有限元软件进行无阻尼谐响应仿真的主要步骤为：

(1) 建模：在 ansys自带的三维建模模块spaceclaim 中建立金属半球谐振子三维模型，并设置材料性质和几何性质。本文先建立了半球谐振子模型，沿半球唇缘均匀分割出72个0.5 mm×0.5 mm的载荷作用区，在模型半球唇缘某对称位置处添加集中质量如图6(a)中A，B所示位置，集中质量所在方位即为某一固有刚性轴(重轴)。仿真模型材料参数设置如表1所示。

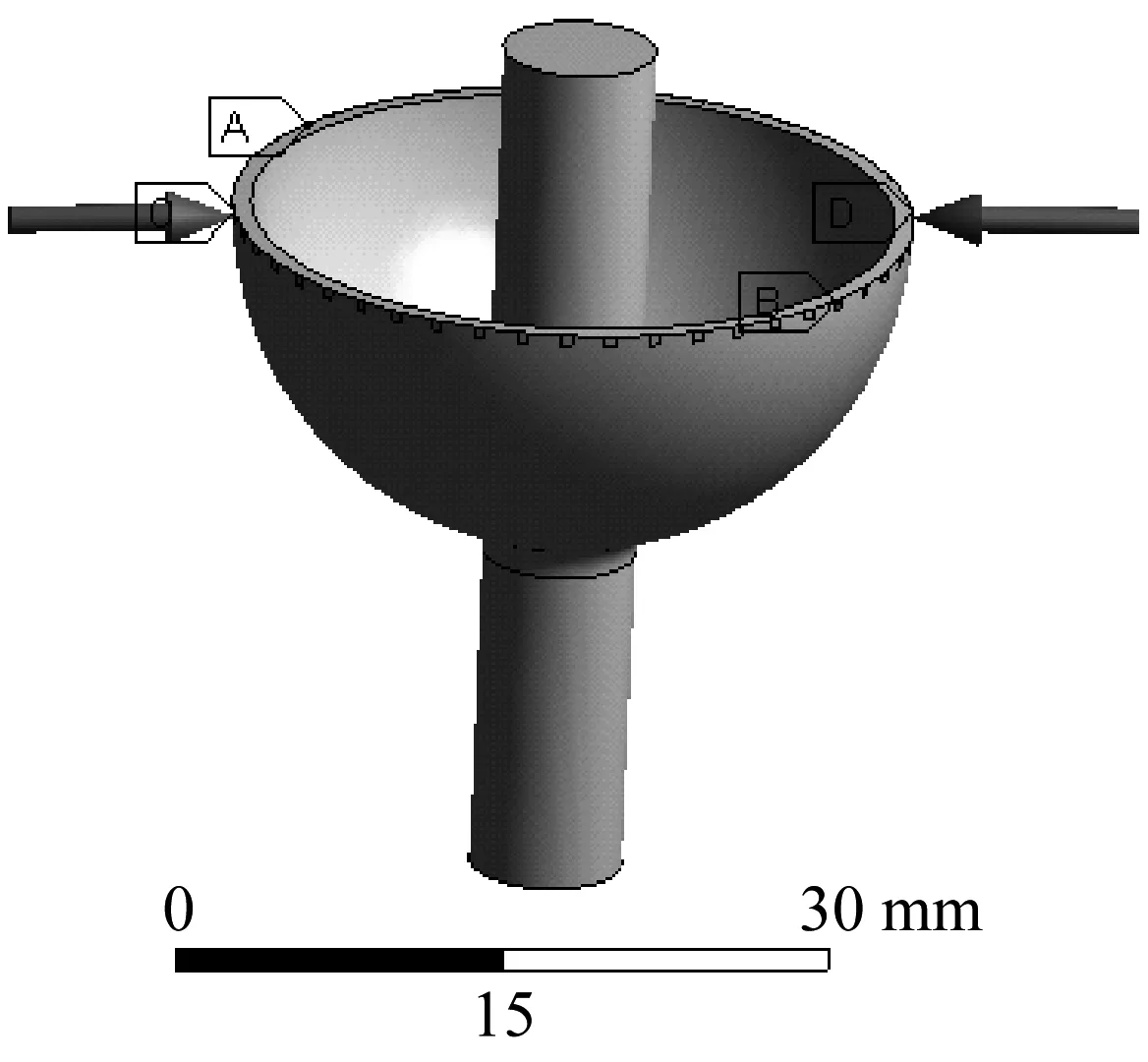
(a) 添加质量和载荷示意图

表1 谐振子模型几何及材料主要参数

(2) 施加约束并进行模态分析：在谐振子支撑柱两端进行位置约束，分别对模型添加缺陷质量前后根据需要求解各阶模态频率，添加缺陷质量前后四波腹模态谐振频率如表2所示。

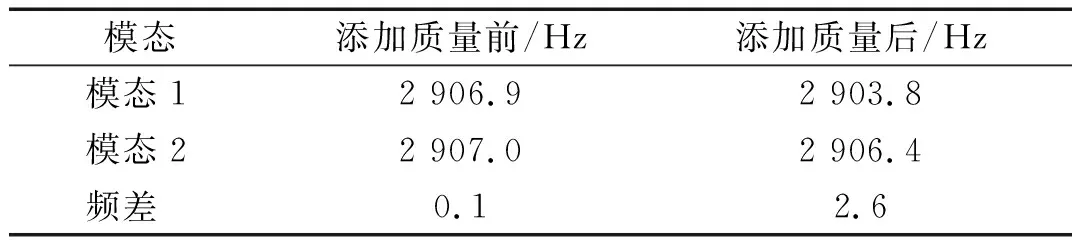
表2 四波腹模态谐振频率

(3) 施加载荷：在一对对称位置上施加大小、频率和相位分别相同的动态载荷，载荷垂直作用于谐振子外球面上如图6(a)所示。

(4) 设置频率范围并求解谐响应结果：根据模态分析所得到的四波腹振动的谐振频率，设置谐响应的求解频率范围和子步数以确定施加载荷的频率序列。求解后根据需要提取半球唇缘载荷施加位置的谐响应幅频曲线结果。

谐响应仿真设置的主要参数如表3所示。

表3 谐响应分析主要参数设置

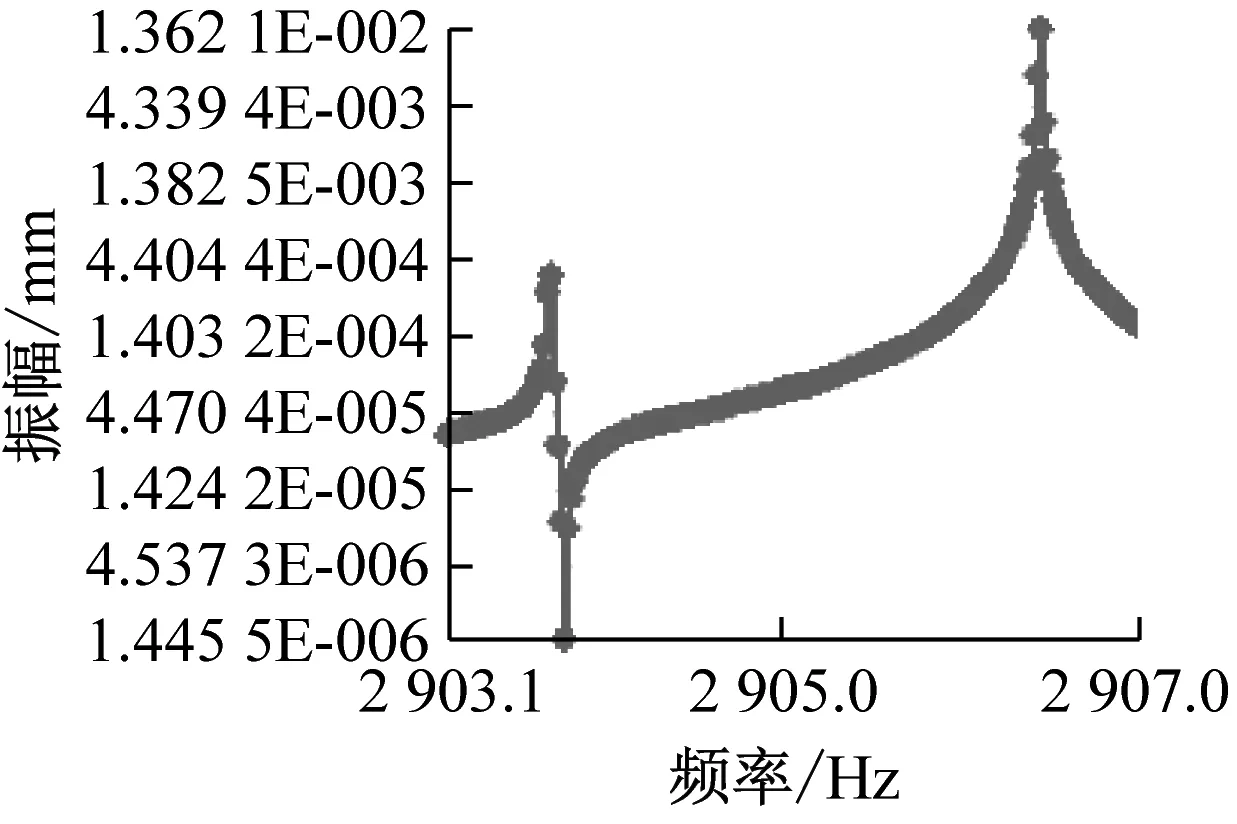
在对称位置添加缺陷质量后，谐振子四波腹振动模态将出现两个明显不同频率的谐振频率，谐振子沿缺陷质量添加方位的谐振频率略低，此方位为谐振子低频轴(也称为重轴)，与此刚性轴呈45°方向存在另一固有刚性轴为高频轴(也称为轻轴)，其方位示意图如图6(b)所示，在任意90°范围内都可看到两个刚性轴，因此我们选择任一0°～90°范围进行谐响应仿真。选定初始0°位置后，我们将质量对添加在与初始0°夹角呈30°的一对称位置上，按照表3的设置，分别在0°～90°之间均布的18个对称位置上分别加载进行谐响应仿真求解，提取加载位置的频响曲线，在固有刚性轴30°和75°附近的频响曲线如图7所示。

(a) 25°位置

由图7可看出，幅频曲线在固有刚性轴位置仅有一个极大峰值，而在其他位置则出现两个不同频率的极大峰值，这与理论分析的结果相一致，进一步验证了通过扫频激励绘制幅频响应曲线的方法确定固有刚性轴方位角的正确性。

2.2 测量试验结果分析

本次试验中，由有限元仿真确定金属谐振子二阶谐振频率在2 905 Hz左右，调参得到的激励频带为3 050～3 060 Hz，扫频时间为50 s。步骤2的试验参数设置如表4所示。

表4 试验参数及采样参数设置

在0°～90°范围旋转谐振子底座测得对应的幅频曲线。图8所示为激光多普勒测振仪测得的实时信号图，在20°的位置和靠近固有主轴的30°位置测得的振动信号，从图8(b)中可以看出，当激励在相对靠近低频轴的位置时，高频轴位置对应振型只能产生较为微弱的响应，以至于辨识不出高频轴处的振动。0°～90°的幅频曲线如图9所示，幅频曲线反映了两刚性轴位置对应模态振型振幅峰值随激励位置的变化，其振幅峰值记录在表5中，振幅峰值随角度呈现类似正弦变化的规律。由于在30°、35°和75°、80°处的曲线中只能观察到一个峰值，因此可判断固有刚性轴在30°、35°和75°、80°之间。

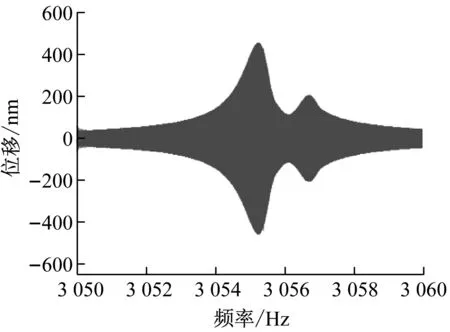
(a) 旋转20°测得

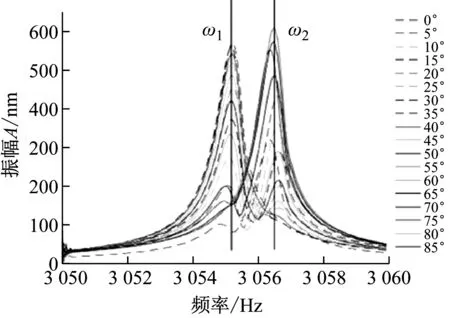
图9 幅频曲线

表5 不同位置两轴系对应模态振型的峰值

为进一步确定固有刚性轴的具体方位，在步骤2结果的基础上采用30°和75°位置对应的谐振频率分别作为激励频率进行步骤3波节点振幅的测量。旋转谐振子底座使激励相对地在30°～35°范围内以1°步进角进行旋转，测量谐振子唇缘处与激励方位呈45°角的波节点位置的振幅，测量结果如表6和图10(a)所示。为了更加清晰地表示振幅随激励位置的变化关系，这里采用Min-max标准化方法将振幅映射至[0,1]区间，进而绘制出折线图。从图10(a)曲线图可以明显看出激励在33°位置时，波节点的振幅最小，因此可确定固有轴位置即此时的激励位置，同样的由表7和图10(b)可得到另一固有轴方位在76°位置。

表6 波节点振幅

表7 波节点振幅

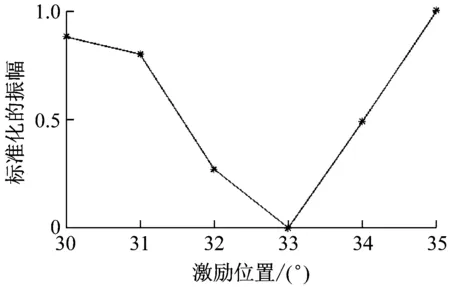
(a) 激励位置在30°～35°

综上所述，通过连续扫频激励和稳定频率的正弦激励相结合，利用激光测振仪绘制谐振子幅频特性曲线和检测振幅的方法，最终在确定初始0°的情况下，测得两个不同频率的四波腹振型对应的固有刚性轴的位置分别在33°和76°的位置，基于旋转台的最小步进角，此测量试验的角度分辨率优于1°，试验测得的两固有轴夹角为43°，与理论上两刚度主轴之间的夹角45°相差约2°，其辨识相对误差约为4.4%，在可接受范围内。

2.3 结果与讨论

谐响应仿真中，已知固有刚性性轴位置，模拟了在不同激励位置扫频绘制频响曲线的过程，得到的频响曲线沿固有轴变化的规律与理论分析相符。在固有轴测量试验中，测量结果中谐振子激励位置的幅频曲线沿固有刚性轴的变化趋势与仿真结果具有一致性，由于仿真较为理想且忽略了阻尼，因此仿真曲线更为锐利，变化比较明显，而实际测量试验在5°范围内已不能从幅频曲线中辨识到两个谐振峰。因此试验中粗略确定固有轴位置后，在固有轴位置附近通过正弦激励信号激励其四波腹振型，并检测振型波节点振幅随激励位置的变化，有效提高了检测精度。该测量平台相对简单，后续可通过改善夹持装置和其他调节装置提高装置定位精度，通过更小的旋转角度提高测量分辨率及提高激励振幅等方式，进一步提高固有刚性轴的测定精度。